闸机通行检测点的多级分布设计法

茅 飞

（南京康尼电子科技有限公司，江苏 南京 210038）

0 引言

在城市轨道交通的自动售检票系统（AFC）中，采用闸机设备（包含附属设备）及其内部的智能识别系统对乘客通行行为进行识别，实现自动检票的目的。现阶段，我国城市轨道交通中闸机设备的检测部分大多利用稀疏红外传感器采集数据的方式，对乘客通行情况进行判别。实际通行序列状态非常多，情况复杂。以16点设计为例，瞬时状态数目达6万种以上，从理论上讲，可能序列情况是不可数的，若限制时间离散状态为基本数目32为例，可能序列状态数目超过280万亿种。由于红外检测数目、检测点稀疏分布与识别速度、识别率密切相关，在指定红外检测数目的情况下，闸机智能识别系统的稀疏红外传感器位置布局就显然至关重要。

1993年，Niyogi与Adelson提出了XYT模型，该模型根据双绞线模式和直线模式对运动目标进行步态识别[1-2]。1997年，Cunabo等将腿部建模为链接的钟摆，并从其倾斜角度信号的频率分量中获取步态特征[3]。2005年，曲日基于人体步态识别提出了一种基于事件驱动的乘客通行算法[4]。2008年，牟总斌进一步提出了一种将人体头肩部与步态检测的闸机相结合的通行逻辑算法[5]。2009年，王建荣以红外传感器采集通行数据为基础，将连续状态的XYT模型改进成离散状态的步态识别算法[6]。2012年，马志伟等采用半监督学习的行人检测方法[7]。刘娜提出了采用步态能量图作为检测的特征，采用保局映射投影（LPP）方法对特征序列进行降维[8]。2013年，卢玉婷将通过闸机的通行目标分为行人和物体两类，基于支持向量机（SVM）提出了标准化矩阵（SM）识别方法，研究了行人模式识别和物体模式识别[9]。钟兴志等通过人的行走方式识别个体的身份[10]。2016年，王小康等将人体识别算法与步态识别算法相结合，提高识别正确率[11]。2017年，作者等结合人体尺寸数据,采用事件及区域识别相结合的方法，分析了乘客的不同行为对传感器状态的影响[12]。2014年，王子甲等研究了两种典型的闸机布置形式,建立了行人仿真优化模型[13]。付佳等研究城市轨道交通车站中检票闸机的平行式布局和垂直式布局[14]。

本文针对双类别的通行检测问题，以序列图像数据为训练样本，提出了动态多级相异区域的概念，建立了正负样本双动态多层次检测点设计模型，给出了多级分布设计算法和多层次强分类识别算法。

1 双动态多层次检测点设计模型

1.1 双动态设计模型

红外传感器的设计是有范围限制的。设红外传感器位置设计范围为DXY⊂×，则任意xD∈都可能是红外传感器所在位置，即可能设计点。

图 1为设计区域及设计示例图，其中的浅灰色部分对应的方角矩形为最大设计区域XY×（即最大宽度、高度分别为X、Y），深灰色部分对应的圆角矩形为可设计区域D，15个黑色点为设计点。

设 P = { pi(x,y) |i = 1,2,… ,Pn}和 N = {nj(x,y )|j = 1 ,2,… , Nn}分别为正例（单人通行）、负例（双人通行）序列图像数据集。

图2为实际数据集的部分数据。其中白色（值为 1）区域为通行目标的二值化图像，黑色（值为0）为非通行目标的二值化图像。

图2 实际数据集的部分数据Fig.2 The actual data part of the data set

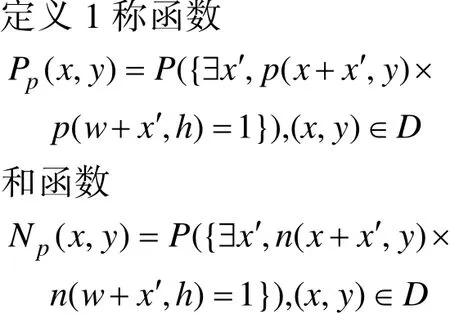
分别为 p = ( w,h ) ∈ D 下的正例和负例位置分布函数。其中 P (⋅)为概率测度。

显然，正例和负例位置分布函数都具有局部不变平移性，即在可行域范围内有下面的性质。

性质 1（正例平移不变性） 若 x ∈[0,x']∪[X - x ′,X]满足 P (x,y)= 0 ，则

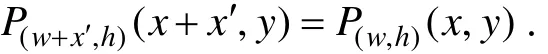
性质 2（负例平移不变性） 若 x ∈[0,x']∪[X - x ',X]满足 N (x,y)= 0 ，则

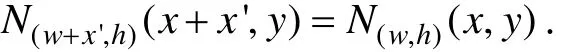
定义2称函数 N Pp(x,y)＝|Np(x,y)－ Pp(x,y)|为 p = ( w,h ) ∈ D 下的相异函数。

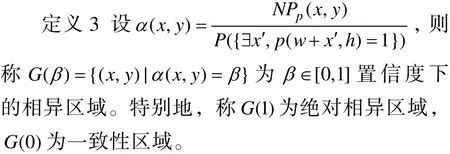
定义4 双动态设计模型是指训练样本在双点设计的条件下，以MLE为估计方法，实现静态特征化的设计方法，即该模型的设计点(p,q)点满足

点(p,q)称为双动态设计点。

1.2 多层次设计模型

显然，双动态设计模型是以最大激活样本数目为基础，识别最大负样本数目的方法，达到样本识别率最优的目的。

定义4 称集类

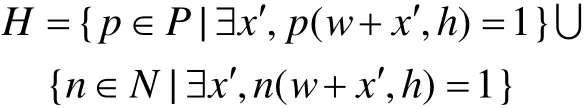
为双动态设计模型的激活样本。

记P1= P,N1= N。若双动态设计模型训练样本为 Pn∪Nn，激活的正负例样本为Pgn⊂Pn、Ngn⊂Nn且激活样本中识别错误的正负例为P′⊂Pn、N′⊂Nn，则记Pn+1= PnP′、Nn+1= Nn/N′。

定义 5 以 Pn∪Nn,n =1,2,…为训练样本的双动态设计模型称为n级双动态设计模型。这些模型的集合称为多层次设计模型。称 M =min{n|Pn∪Nn=Φ , n =1,2,…} 为多层次设计模型的最大阶数（或最高层次）。

通行识别算法以所有n( n = 1 ,2,… ,M )级双动态设计模型为弱分类器组成的强分类器为多层双动态设计模型。具体的算法可采用级联分类器、Adaboost算法等实现通行识别，在此不详细讨论。

静态模式识别只考虑瞬时状态的形态特征，不考虑前后之间的关系。

理论上可以证明：在静态模式下，若正常形态集和异常形态集相互不交时，即没有共同形态时，通过设计至多可数个检测点就可以区分正常形态和异常形态这两种状态。

考虑到实际设计点的有限性，实际设计达到一定的要求即可，例如达到最低识别率、最大循环次数等。

根据多层次设计模型，得到如下的多级分布设计算法。

算法：多级分布设计算法。

输入：可设计区域D；训练样本P∪N；最低识别率Ma；最大循环次数T。

输出：多层次设计模型的最大阶数M；所有阶数的双动态设计点。

方法：双动态设计模型。

过程：

（1）初始化 n =1， P1= P， N1= N；

（2）根据 Pn和 Nn的递推公式，计算 Pn∪Nn；

（3）根据双动态设计模型，计算设计点( pn, qn)；

（4）若 Pn∪ Nn=Φ(即 n = M)，转（8）；

（5）若n＞T,转（8）；

2 多级分布设计算法

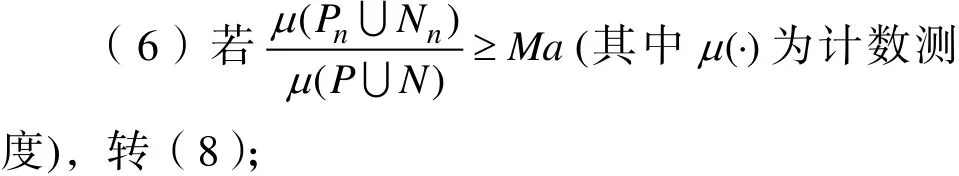
（7）赋值n为 1n+ ，转（2）；

（8）输出结果。

3 图像序列数据下的设计仿真

仿真实例选择单人通行图像序列为正样本，双人通行图像序列为负样本。在本文中的图2及本例中的正负样本使用了中国科学院自动化研究所收集的 CASIA 步态数据库[15]。

3.1 正负例位置分布函数的仿真实现

图 3（a）（b）以 CASIA 步态数据库的部分单人行走图像序列数据及其复合的双人行走图像序列数据为正负样本，运用本文提出的正负例位置分布函数的概念绘制了（a）不限制高度和（b）限制高度两种情况的位置分布函数的仿真结果图。

3.2 双动态设计模型的仿真实现

图4使用与图3中采用的相同数据，运用双动态设计模型，实现了（a）不限制高度和（b）限制高度两种情况的双动态设计点。其中，白色圆角框内的两个“十字点”双动态设计点，外侧“十字点”为通行启动和终止点。图4中的设计点是根据实际通行检测的双向通行现实，而采用的对称式设计。

图3 正负例位置分布函数的仿真结果图Fig.3 Location distribution function of cases

图4 双动态设计模型的仿真设计图Fig.4 Double dynamic simulation model design

4 结论

本文以图像序列数据为训练样本，针对双类别的通行检测问题，提出了一种闸机通行的红外传感器布局方法，在样本数据区域分布的基础上，建立了双动态多层次检测点设计模型，并给出了多级分布设计算法，仿真了分布设计法的实现效果图。闸机通行数据中是连续的图像序列数据，实际红外传感器的数目较少，采取稀疏识别方式识别连续数据，通常特征数据是不完整的，因此连续图像序列数据的稀疏特征化是红外传感器布局的一个有价值的研究问题。

参考文献

[1] Polana R, Nelson R. Detecting Activities[J]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition,1993, 3(5): 2-7.

[2] Niyogi,S., Adelson, E. Analyzing and recognizing walking figures in XYT[C], Computer Vision and Pattern Recognition,1994: 469-474.

[3] Cunado, D., Nixon M., Carter, J. Using gait as a biometric,via phase-weighted magnitude spectra[R]. Proceedings of International Conference on Audio- and Video-based Biometric Person Authentication, Crans- Montana, Switzerland, 1997: 95-102.

[4] 曲日. 城市轨道交通中闸机智能识别系统及其识别技术的研究[D]. 天津: 天津大学, 2005.

[5] 牟总斌. 基于人体头肩部与步态检测的闸机通行逻辑[J].城市轨道交通研究, 2008, 8: 36-39.

[6] 王建荣, 王庆节, 曲日, 喻梅, 任长明. 传感器通道中的运动模式的步态识别算法[J]. 计算机应用, 2009, 29(8): 2092-2094, 2108.

[7] 马志伟, 崔荣一, 金小峰. 基于半监督学习的行人检测方法研究[J]. 软件, 2012, 33(6): 23-36.

[8] 刘娜. 基于步态能量图的特征提取[J]. 软件, 2012, 33(9):119-121．

[9] 卢玉婷. 基于SVM的闸机目标识别方法的研究[D]. 南京:南京理工大学, 2013.

[10] 钟兴志, 王晨升, 刘丰, 郭世龙. 步态识别综述[J]. 软件,2013, 34(4): 160-164.

[11] 王小康, 徐骏善, 周凡. 闸机中智能通行识别技术的研究[J]. 机械制造与自动化, 2016, 45(2): 225-227.

[12] 茅飞, 孔慧慧, 李宏胜, 康玉芳, 朱伟. 轨道交通车站闸机智能识别研究[J].城市轨道交通研究, 2017, 20(12): 123-126.

[13] 王子甲, 陈峰, 罗诚. 轨道交通车站检票闸机布局的仿真优化[J]. 北京交通大学学报, 2011, 35(6): 28-32, 39.

[14] 付佳, 李季涛, 边可. 轨道交通车站检票闸机布局的仿真研究[J]. 铁道运输与经济, 2014, 36(1): 88-92.

[15] 中国科学院自动化研究所. CASIA 步态数据库[DB/OL].http://www.sinobiometrics.com或者http://www.cbsr.ia.ac.cn/china/Gait%20Databases%20CH.asp.2010-10-09.