一种改进的MVU降维方法

王洪东，贾宏哲，吴晓婷

（辽宁师范大学 计算机与信息技术学院，辽宁 大连 116081）

0 引言

流形学习目前已经成为机器学习、数据挖掘中的研究方面[1-3,12]。近年来，已经有很多流形学习的方法相继提出，如 Maximum Variance Unfolding(MVU)[4]、ISOMAP[6]、局部线性嵌入（Locally Linear Embedding LLE）[7]、拉普拉斯特征映射（Laplacian Eigenmaps, LE）[9]，局部切空间排列[10]（Local Tangent Space Alignment, LTSA）等等。不像ISOMAP只保持测地距离，MVU不仅仅考虑到局部的距离，而且还考虑到近邻点之间的角度间的关系。在技术上，由于 MVU采用了（semidefinite programming, SDP）来处理降维，因此，MVU又被称为（semidefinite embedding，SDE）。MVU算法在降维的应用过程中，存在较大的时间和空间的消耗，为了解决此问题，landmark MVU（LMVU）被提出和应用[5,13,15,16]。该降维方法的提出对降维计算有一定的影响，促进了该领域的发展。文献[14]对该算法的收敛性做了理论研究，文献[17]对该算法也做了应用研究。基于流形学习的思想，充分利用数据的类别信息我们提出一种改进的 MVU算法。该算法充分考虑到了紧邻点的分布关系，能够挖掘数据局部密度信息，从而有效保持高维数据的流形信息实现有效降维。实验结果验证了算法的有效性。

1 MVU算法

MVU是Weinberger和saul等人在2004年提出的一种基于流形学习的非线性降维方法[1]。该方法通过局部的 Gram矩阵保持局部的相似性，在降维过程中保持方差的最大化。利用局部提供的信息，保持整体的几何结构及性质。使得远离的数据点其低维坐标展开得尽可能的远，并且约束保持局部近邻点的欧氏距离不变。这个算法的原理是通过半定规划(SDP)技术学习一个Gram内积矩阵，然后对这个内积矩阵进行特征分解获得全局低维坐标。

MVU算法的具体步骤如下：

Step1.近邻的选取（一般采用K近邻方法）

X ={x1, x2,… xN} ,xi∈RD在高维空间中寻找每个样本点 xi的 k (k ＜N)个近邻点，距离公式为

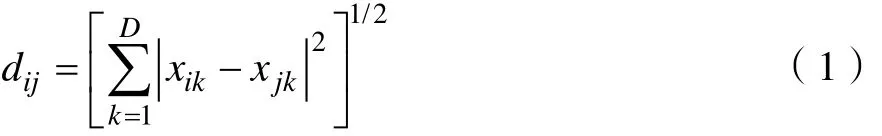
Step2. 通过计算半正定规划（SDP）求内积矩阵K。

设输入观测到的高维数据 x ∈ RD(i = 1,2,… ,n)，i目标输入为低维坐标 y ∈ Rd(i = 1 ,2,… ,n )，要使得远i离的数据点其低维坐标展开的尽可能远，并且约束保持局部近邻点的距离，最直观的目标函数定义为使得地位坐标保持局部近邻的距离而最大化任意两点间的距离之和，即：

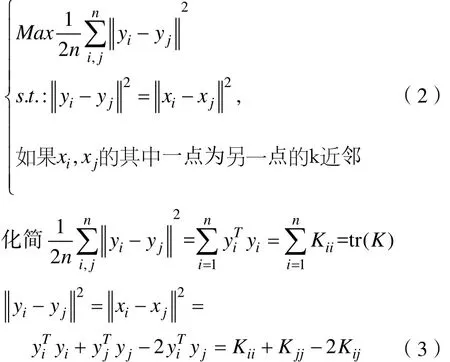
优化问题转化为：保证局部等度规、中心化和半正定等 3个约束条件下使得内积矩阵的迹最大化，即

通过半定规划(SDP)学习内积矩阵丘使得保持局部近邻距离和低维数据点中心在原点，实现最大方差展开，如上式。

Step 3对内积矩阵K进行特征分解求内在低维坐标：求 K的最大的 d个特征值 λ1， …λd(令 Λ=diag(λ1， …λd))对应的特征向量U = [ v1,… vd],则d维坐标为 Y = ΛUT。

2 改进的MVU降维方法

对于给定的高维观测数据集为 X = { x1,x2,…xN} ,xi∈RD，采样自d维流形，求低维坐标Y={ y1,y2,… yN}。设样本点聚类分类的类别个数为C，mj为第 j类样本的中心， n (j)为第 j类样本的个数。则第 j类样本点的类内平均距离为

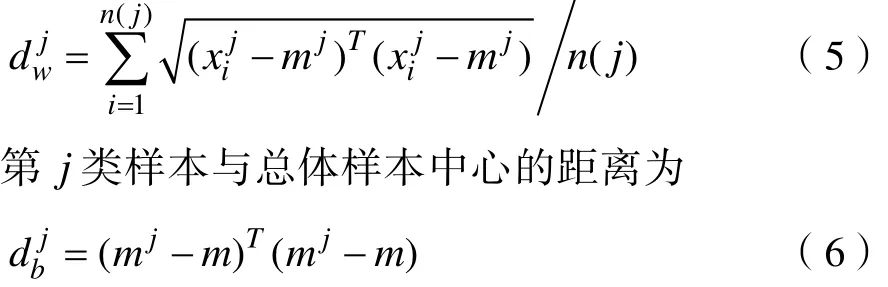
m为总体样本的中心。定义聚类后反映密度信息的密度系数为（其中， j为样本点i所属的类， j = 1 ,2,… C ）在MVU第二步中以 ρij和重构权值构建d维嵌入，即求

改进的 MVU在选取近邻点之前首先对样本进行聚类分类，聚类的中心含有大量的信息，利用类别信息构造重构误差的近似重构系数并体现到MVU计算过程中。

3 实验及结果

分别将改进的 MVU方法用于人脸图像特征降维和基于内容的图像检索，验证算法的有效性。本文实验所采用的聚类方法为模糊 C均值聚类算法[11]。实验中，首先采用改进的MVU方法对人脸特征进行降维，实验所采用的人脸图像数据集frey_raw face中包括同一人脸在不同光照、姿态条件下的2000幅大小为560维（2028×）的灰度图像。数据集的内在特征只包含角度和表情，将原始数据降到2维采用改进的MVU进行降维时，近邻点个数K=12，图1为二维嵌入效果。此外，本文还将改进的 MVU方法应用于基于内容的图像检索，并与应用 MVU进行检索的结果进行了比较。实验选用SIMPLIcity系统使用的测试集（http://wang.ist.psu.edu/docs/related）作为图像库，该测试集选自Corel数据库，共1000幅图像。

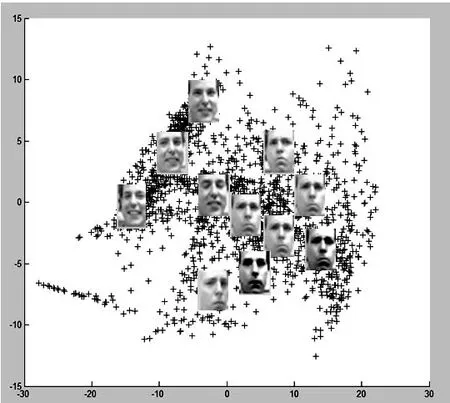
图1 人脸表情二维嵌入结果Fig.1 Two-dimensional embedding of facial expressions

图5 为原MVU方法和改进的MVU方法在维数变化时，查准率的变化情况。从图中可以发现，直到维数达到14时，原MVU和改进MVU才保持了一致的查准率，而在维数较低时，应用改进的MVU方法降维后的查准率普遍较高。

通过实验可以发现，挖掘密度信息的 MVU能够更好的保留原始数据的几何结构，并有效地将不相关图像区分开，从而有效地提高了查准率。

图2 未降维的图像检索结果Fig.2 Image retrieval results without dimensionality reduction

图3 MVU降维后的图像检索结果Fig.3 Image retrieval results after MVU dimensionality reduction

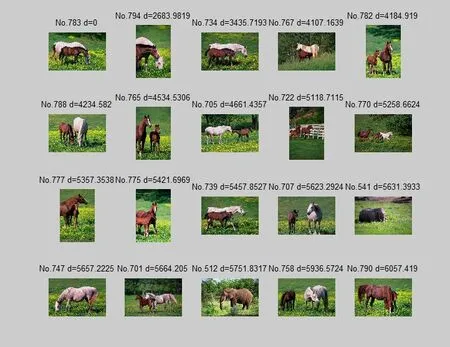
图4 改进的MVU降维后的检索结果Fig.4 Search results after improved MVU dimensionality reduction

4 结束语

本文分析了基于原始的MVU非线性降维方法，提出了一种改进的 MVU降维方法。此方法通过挖掘近邻点之间的密度信息，引入密度系数有效的降低了近邻点的选取对降维结果的影响，并且很好的保留原始数据的几何结构。改进的 MVU方法用于人脸特征提取和图像检索实验，均得到了很好的效果，证明了该方法的有效性。

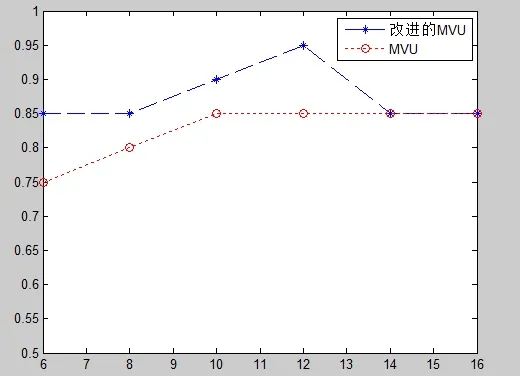
图5 查准率曲线图Fig.5 Precision curve

参考文献

[1] 张小华, 王乐. 一种多尺度和聚类分析的变化检测[J]. 新型工业化, 2011, 1(3): 72-79.

[2] 邢芝会, 孙建德. 流形学习及其在检索中的应用[J]. 新型工业化, 2011, 1(10): 12-20.

[3] 钟彩. 边缘检测算法在图像预处理中的应用[J]. 软件,2013, 34(1): 158-159.

[4] Weinberger K Q, Saul L K. Unsupervised learning of image manifolds by semidefinite programming [C]. IEEE Conference on Computer Vision and Pattern Recognition, 2004, 2:988-995.

[5] Weinberger K Q, Packer B D, Saul L K. Nonlinear dimensionality reduction by semidefinite programming and kernel matrix factorization. In R. G. Cowell & Z. Ghahramani (Eds.)[C]. Proceedings of the 10th international workshop on artificial intelligence and statistics, 2005, 381–388.

[6] Thnenbaum J B, de Dilva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J].Science, 2000, 290(5500): 2319-2323.

[7] Roweis S T, Saul L k. Nonlinear dimensionality reduction by locally linear embedding. Science, 2000, 290(5500): 2323-2326.

[8] 张小华, 王然. 基于图像特征的偏微分方程去噪方法[J].新型工业化, 2011, 1(6): 9-14.

[9] Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation,2003, 15(6): 1373-1396.

[10] Zhang Z Y, Zha H Y. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J].SIAM Journal on Scientific. Computing, 2004, 26(1): 313-338.

[11] Bezdek J C, Ehrlich R, Full W. FCM: The fuzzy C-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2):191-203.

[12] 贺霖, 阮蔚桐, 张梅, 等. 基于支持向量机的高光谱图像分类方法综述[J]. 新型工业化, 2012, 2(1): 46-51.

[13] Liu X, Shi L. Fuzzy C-Mean Clustering Image Segmentation Algorithm Research for Sport Graphics Based on Artificial Life[J]. Applied Mechanics and Materials, 2013, 263(1):2207-2210.

[14] Arias-Castro E, Pelletier B. On the convergence of maximum variance unfolding[J]. Journal of Machine Learning Research , 2013, 14(1): 1747-1770.

[15] 袁爱领, 齐伟, 钱旭. 基于流形正则化的支持向量机文本分类[J]. 软件, 2013, 34(2): 65-68.

[16] Michael Gashler, Dan Ventura, Tony Martinez. Manifold Learning by Graduated Optimization[J]. IEEE Transactions on Systems Man and Cybernetics Part B, 2011, 41(6): 1458-1469.

[17] Chihang Wei, Junghui Chen, Zhihuan Song. Developments of two supervised maximum variance unfolding algorithms for process classification[J]. Chemometrics and Intelligent Laboratory Systems, 2016, 159(15): 31-44.