储层衰竭式开发过程中的流固耦合数值模拟研究

马都都

（西安石油大学石油工程学院，陕西西安 710065）

在储层衰竭过程中，流体采出使得井眼周围孔隙压力减小，导致储层产生的体积应变，进而导致渗透率减小，同时渗透率减小又影响孔隙流体流动和孔隙压力分布[1-4]，渗透率作为影响储层流体渗流最主要的参数，在常规的油藏数值模拟中被视为常数，使模拟结果与实际情况有较大的误差。为了使储层开发渗流机理更加符合实际，本文推导了流固耦合作用下储层开发过程中渗透性随体积应变、储层温度、孔隙压力变化的动态演化模型，给出了以单元节点位移和单元节点孔隙压力为未知量的储层流固耦合的非线性有限元增量方程，同时对ABAQUS场变量用户子程序进行了二次开发，在ABAQUS进行主要未知变量求解过程中，其结果会传递到子程序计算后输出，从而实现基于ABAQUS有限元平台的储层开发过程流固耦合效应全耦合数值计算，模拟计算结果对储层开发的长远规划以达到稳产与高产提供了重要的理论依据。

1 流固耦合效应控制方程

众所周知，岩石力学平衡方程及渗流方程的矩阵形式：

（1）平衡方程：

（2）渗流方程：

直接耦合方程得：

其中：

2 储层渗透率动态演化模型

一般储层变形为小变形，基于小变形理论，忽略二阶微量，得：

2.1 动态模型Ⅰ

基于理想毛管束岩石模型，考虑储层的体积变化近似为孔隙体积变化，由砂岩孔隙度φ、渗透率K、孔隙半径r的关系[5]及孔隙度与体积应变的关系[6]得：

2.2 动态模型Ⅱ

假设砂岩骨架颗粒体积及表面积的变化仅由热胀冷缩引起，并且所有砂岩颗粒为等直径球形，基于Kozeny-Carman 渗透率方程，得

再由表面比、体积应变、孔隙度的定义，得：

又由 ΔVp=εvVb-（Vb-Vp）γΔT，代入上式得到忽略砂岩颗粒表面积变化的情况下，储层渗透率随体积应变和储层温度变化的动态演化模型[6]：

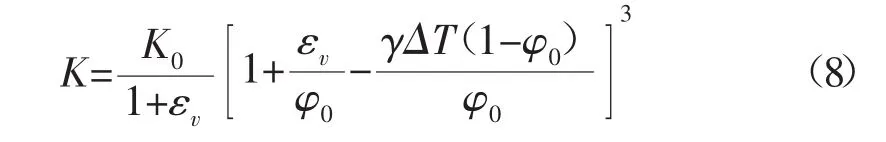
2.3 动态模型Ⅲ

考虑储层体积应变、孔隙压力变化、储层温度变化对渗透率的影响，推导新的渗透率动态演化模型。由有效应力原理可知，当流体从储层中采出时，孔隙压力就会减小，而外应力即围压保持不变，因而有效应力就会相应增大，使砂岩骨架被压缩[7，8，9]。由砂岩骨架有效应力dσs与孔隙压力变化dp、孔隙度φ之间的关系，结合砂岩骨架弹性模量Es与砂岩杨氏模量Eb及孔隙度φ的关系[10]，则储层温度变化与孔隙压力变化共同作用导致砂岩骨架的变形量为

其中：φ＝（φ0+εv）/（1+εv）

代入式（7）得到忽略砂岩颗粒表面积变化的情况下，储层渗透率随体积应变、孔隙压力变化、储层温度变化的动态演化模型：

3 流固耦合作用下储层衰竭式开发数值模拟研究

就新疆昌吉油田某致密砂岩储层，利用ABAQUS有限元软件对一油藏中心有一口采油井进行模拟分析，采用衰竭式开采方式，并和未考虑储层物性参数动态变化的计算结果进行对比。

3.1 模拟参数与边界条件

图1 有限元模型

模拟的衰竭式开发储层的尺寸为：200 m×200 m，有限元模型（见图1），模拟衰竭式开发时间为300 d，井底生产流压为20 MPa，由于为衰竭开发，设定四周边界孔隙压力由37 MPa衰减为30 MPa，模拟计算了该开发过程中的流固耦合作用，并与储层渗透率为恒定值时的模拟计算结果进行对比，其他模拟参数（见表1）。

表1 储层模拟参数

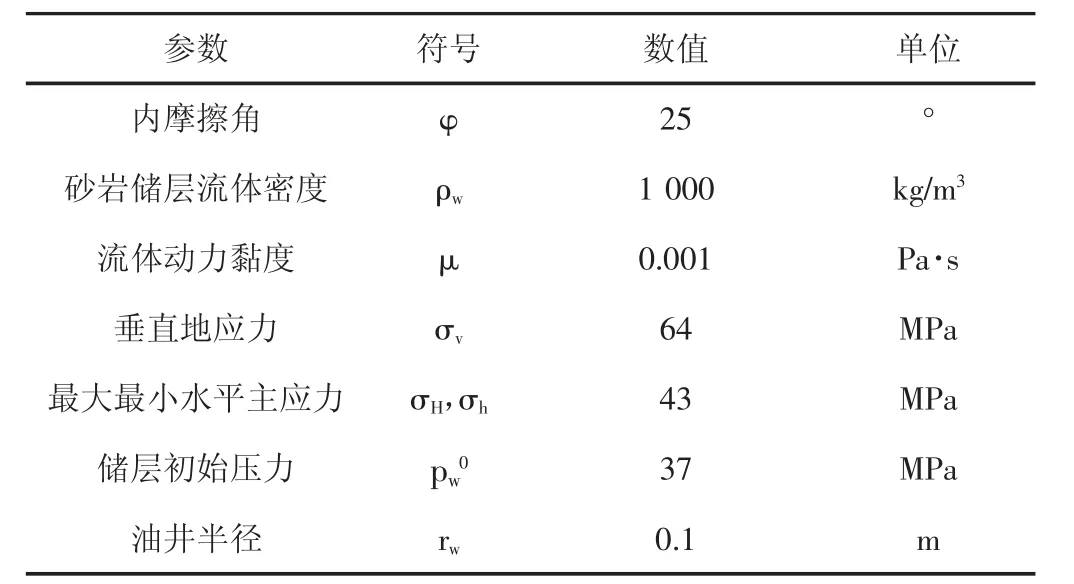
表1 储层模拟参数（续表）

3.2 模拟结果

3.2.1 储层压力分布 井底以定流压20 MPa生产，而远场边界孔压由37 MPa线性递减为30 MPa，则整个模拟区域的孔隙压力状态将重分布，其中不同开发时间储层孔隙压力随距井眼不同距离的变化曲线（见图2），可以看出，井眼周围孔隙压力呈漏斗状分布，越靠近井眼，孔压越小。同时，随开发持续，整个储层压力衰竭，可见由于远场压力衰减，无法为采液提供能量，所以在衰竭式开发方式下开发一段时间后，需调整开发方案。

图2 不同开发时间储层孔隙压力随空间变化曲线

图3 开发300 d时储层体积应变、孔隙度、渗透率比K/K0分布

3.2.2 储层物性参数动态变化 由于储层液体不断采出，储层孔隙压力衰减，导致储层产生压缩体积应变，进一步导致储层渗透率与孔隙度减小，当开发300 d后，储层体积应变、孔隙度、渗透率比K/K0分布（见图3），其中在井眼附近产生的体积应变最大、孔隙度与渗透率的减小最大，其中在开发300 d时，孔隙度减小17.36%，渗透率减小了44.59%。

3.2.3 生产动态变化 显然，考虑了储层开发过程中存在的流固耦合效应时，由于井眼附近孔隙压力梯度、渗透率以及孔隙度发生变化，相比于未考虑流固耦合效应的情况，两者累计产液量存在差异，累计采液量随时间变化曲线（见图4），可以看出，开发300 d时，考虑了流固耦合作用时的累计采液量比不考虑流固耦合作用时的累计采液量小569 m3，且两者间的差值随开发时间延长将持续增大。

图4 定压生产不同生产时间点累计产液量

4 结论

储层衰竭式开发过程数值模拟研究结果显示：

（1）开井后采油井眼附近大范围内的孔隙压力呈漏斗状递减，随开发时间延长，孔隙压力减小的范围不断扩大，因此当储层供液能力较差时，固定生产流速，地层压力将大幅衰减，无法长时间稳产。

（2）由于采油井眼附近大范围内的孔隙压力呈漏斗状递减，导致产生的压缩体积应变也呈漏斗状分布，即在井眼周围最大，沿井眼径向向边界处递减；进一步导致的孔隙度与渗透率损失量也同步递减。

（3）考虑了流固耦合的开发过程，相比不考虑流固耦合的情况，前者的累计采液量比后者小569 m3，且两者之间的差值随开发时间延长将持续增大。

以上研究结果证明基于ABAQUS有限元软件对储层开发过程中的流固耦合数值模拟，对于更准确模拟储层的开发动态，从而指导储层开发的长远规划具有一定的参考价值。

参考文献：

[1]周志军.低渗透储层流固耦合渗流理论及应用研究[D].大庆：大庆石油学院，2003.

[2]郭尚平.渗流力学进展[M].北京：石油工业出版社，1996.

[3]Lewis R W，Sukinnan Y.Finiet element modeling of therephase flow in deforming saturated oil reservoirs[J].Int.J.Num.Anal.Methods Geomash，1993，（17）：577-598.

[4]董平川，徐小荷，何顺利.流固耦合问题及研究进展[J].地质力学学报，1999，5（3）：17-25.

[5]孙明，李治平，樊中海.流固耦合渗流数学模型及物性参数模型研究[J].石油天然气学报，2007，26（9）：115-119.

[6]冉启全，顾小芸.油藏渗流与应力耦合分析[J].岩土工程学报，1998，20（2）：69-73.

[7]李传亮.岩石压缩系数与孔隙度的关系[J].中国海上油气（地质），2003，17（5）：355-358.

[8]李传亮.多孔介质的应力关系方程[J].新疆石油地质，2002，23（2）：163-164.

[9]张广明，刘合，张劲，等.储层流固耦合的数学模型和非线性有限元方程[J].岩土力学，1998，19（1）：64-70.

[10]LEWIS R W，SCHREFLER B A.The finite element method in the deformation and consolidation of porous media[M].New York：John Wiley and Sons Inc，1987：287-290.