安徽二期成品油管道顺序输送的运行分析

李鑫伟

〔中国石化销售有限公司华中分公司 湖北武汉 430023〕

1 安徽二期管道概况

中国石化安徽二期成品油管道是将安庆石化的成品油输送到合肥油库、淮南油库、阜阳油库和蚌埠油库，以满足管道沿线合肥、淮南、阜阳和蚌埠等地区的成品油市场需求。管道全长519.4 km，管道设计压力9.5 MPa，管道入口设计输量为410×104t/a。全线采用密闭工艺顺序输送92号汽油、95号汽油、0号车用柴油和0号普通柴油两大类4个品种。各段间距、管径、管容及设计压力见表1。

表1 安徽二期管道沿线管段一览表

管道沿线设置18座线路截断阀室(其中4座为远控阀室)、9座阴极保护站和10座光通信站。全线自动控制采用SCADA系统，沿线各站场与调度中心采用光缆传输方式进行数据交换，调度中心通过各站的站控系统对全线进行数据采集及控制，并负责编排批次、批量计划、输送方案、跟踪批量、泄漏检测和优化运行等。输送流程为：

本文以安徽二期成品油管道为例，依据成品油管道水力特性和顺序输送理论，对该管道各管段的临界雷诺数、临界流量、水力摩阻系数等数据进行计算和分析，并总结出适合各管段的水力计算公式，为配泵和高效节能运行提供理论依据。

2 临界雷诺数Re、混油临界雷诺数Rec和临界流量Qc的计算

2.1 临界雷诺数Re的计算

管线和所输成品油的流动状态用临界雷诺数表示式(1)：

(1)

式中：Q——油品在管路中的体积流量，m3/s；

d——管道直径，m；

ν——油品的运动粘度，m2/s。

管壁相对当量粗糙度ε计算，如式(2)：

(2)

式中：e——管壁的绝对当量粗糙度，m。

光滑区与混合摩擦区的临界雷诺数计算，见式(3)：

(3)

混合摩擦区与粗糙区临界的雷诺数计算，见式(4)：

(4)

2.2 混油临界雷诺数Rec的计算

采用奥斯汀和柏尔弗莱由雷诺数Re与无因

次量C2/Ld的关系总结出的经验公式(5)：

(5)

2.3 临界流量Qc的计算

临界流量的计算公式(6)如下：

Qc=3 600πdvRec/4

(6)

式中：QC——临界流量，m3/h；

d——管道内径，m；

ν——油品的运动粘度，m2/s；

Rec——混油临界雷诺数。

式(5)、(6)的计算结果见表2。当雷诺数ReRe>Re1时流态处于混合摩擦区，当Re>Re2时流态处于粗糙区，此时混油长度则随雷诺数的减小增长较为缓慢。故参考表2计算结果，顺序输送过程中当管道存在混油头时，应保证各管段的混油界面雷诺数Re>Rec，最小流量Qmin>QC，以防因管输流量小而产生大量混油。

表2 混油临界雷诺数Rec和临界流量Qc的计算结果

3 沿程水力计算

管道输油过程中压力能的消耗主要包括两部分，一是用于克服地形高差所需的位能；二是克服油品沿管路流动过程中的摩擦及撞击产生的能量损失转换成的液柱高度，通常称为摩阻损失。长输管道的摩阻损失主要由通过直管段所产生的沿程摩阻和通过各阀件、管件所产生的局部摩阻组成。而长输管道站间管路的摩阻损失主要是沿程摩阻，局部摩阻只占1 %～2 %。

因此，为了计算各控制点在不同工况下的压力控制值，首先需用达西公式计算推导出列宾宗公式，再由列宾宗公式计算出沿程摩阻大小，最后由管道全线压力供需平衡关系式计算出压力控制值。

水力摩阻系数计算，如式(7)：

(7)

式中：A、m根据雷诺试验可知水力摩阻系数λ与不同流态下流体的雷诺数有关，因此得到不同流态下与雷诺数相关的常数系数A、m。

达西公式如式(8)：

(8)

式中：V—油品在管路中的流速，m/s；

hl—管路的沿程摩阻损失，m；

L—管道长度，m；

d—管道直径，m；

g—重力加速度，取9.81 m/s2。

(9)

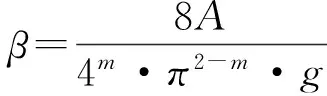
式中：Q——油品在管路中的体积流量，m3/s；

d——管道直径，m；

ν——油品的运动粘度，m2/s；

L——管道长度，m；

A、m——不同流态下与雷诺数相关的常数系数；

β——列宾宗公式(9)含A、m的简化替代量。

各流态区的A、m、β值及沿程摩阻计算式见表3。

得出各流态下流体对应的沿程摩阻计算公式后，将其代入管道全线压力供需平衡关系式中即可求得各工况下各管段沿程摩阻损失的计算值。通过实际值与计算值比较可以得到误差系数，具体记录数据见表4。

假设一条管道有N座泵站，且泵站特性相同，全线管径相同，无分支，首站进站压头和各站内摩阻均为常量，可写出全线的压力供需平衡关系式(10)如下

Hs1+NHY-N×hm=HI+(Z2-Z1)+Hs2

(10)

式中：Q——全线工作流量，m3/s；

N——全线泵站数；

Hl——管道沿程摩阻值，m液柱；

Hs1——管道首站进站压头，m液柱；

Hs2——管道终点剩余压头，m液柱；

HY——泵站扬程，m；

Z1、Z2——管道起、终点高程，m；

hm——每个泵站的站内损失，m液柱。

表3 不同流态时的A、m、β值及列宾宗公式

表4 安徽二期各管段不同工况下运行的记录数据

通过采集数据将其代入公式(10)即可得到实际各管段在不同工况下沿程摩阻损失值。再通过式(7)、(8)、(9)及表3对应公式计算出相应的沿程摩阻损失值。由计算值和实际值比较得到的各管段在不同工况下的误差系数见表5。由此值可以更加准确地计算各管段的摩阻损失，为配泵和高效节能运行提供了理论依据。各段管道在不同工况下的误差系数见表5。

表5 各段管道在不同工况下的误差系数

由表5可知，安徽二期管道各管段在单输汽油时计算摩阻损失值与实际摩阻损失值相差过大，因此在计算时不可以用列宾宗公式。由于安合二期管道各管段在单输汽油时流态均由水力光滑区进入混合摩擦区，可见列宾宗公式在混合摩擦区计算时误差较大。

Moody图是由自然粗糙管实验得出，Cole-brook-White(以下简称C-W)公式(11)为：

(11)

该公式综合了光滑管路普朗特公式和粗糙管尼古拉兹公式得出的，又经实验修正。因此C-W公式被公认为计算水力摩阻系数λ的精确性标准。遗憾的是，公式(11)为一隐函数，必须用迭代方法才能求解，不便于工程应用。下面介绍几个混合摩擦区的摩阻系数公式均为显函数形式，以此来确定安徽二期管道各管段混合摩擦区计算公式。

Jain公式(12)：

(12)

Swamee&Jain公式(13):

(13)

Haaland公式(14)：

(14)

Manadilli公式(15)：

(15)

将表4安徽二期各管段单输汽油数据代入式(12)、(13)、(14)和(15)中得到表6、表7、表8、表9。

表6 安庆—合肥段单输汽油数据

表7 合肥—淮南段单输汽油数据

表8 淮南—阜阳段单输汽油数据

表9 淮南—蚌埠段单输汽油数据

由表6、表7、表8和表9可知，Haaland公式更适合安庆至合肥段及合肥至淮南段单输汽油时沿程摩阻的计算，计算值与实际值相比很小。在淮南至阜阳段及淮南至蚌埠段时，虽然Haaland公式比列宾宗公式更加精准但误差仍较大，因此需要进行系数调整，以求出符合各管段的沿程摩阻系数计算方程。

通过对式(14)改编，得到符合淮南至阜阳段及淮南至蚌埠段公式(16)：

(16)

将表4淮南至阜阳段及淮南至蚌埠段单输汽油数据代入式(16)中得到表10。

表10 改编公式计算数据

4 结语

(1)通过理论计算，确定安徽二期各管段混油临界雷诺数Rec和临界流量Qc，其中

安庆—合肥段，Rec=54 927，Qc=268.246 m3/h；

合肥—淮南段，Rec=45 591，Qc=176.611 m3/h；

淮南—阜阳段，Rec=40 058，Qc=129.838 m3/h；

淮南—蚌埠段，Rec=40 058，Qc=129.838 m3/h。

(2)安徽二期各管段适用的水力计算公式分别为：

安庆—合肥段单输柴油时：列宾宗公式，单输汽油时：Haaland公式；

合肥—淮南段单输柴油时：列宾宗公式，单输汽油时：Haaland公式；

淮南—阜阳段单输柴油时：列宾宗公式，单输汽油时：Haaland改编公式；

淮南—蚌埠段单输柴油时：列宾宗公式，单输汽油时：Haaland改编公式。

参考文献

[1] 严大凡.输油管道设计与管理[M].北京：石油工业出版社，1986.

[2] 夏于飞，张国忠，卜文平，等.成品油管道的运行技术管理[M].北京：中国科学技术出版社，2010:13-56.

[3] 王弥康等.管内单相流体沿程摩阻系数分析[J]，油气储运，1998,17(7)：22-26.

[4] 蒲家宁.紊流混摩区十一个显式摩阻公式的比较[J]，油气储运，1987,6(2)：13-16.