多穿梭板自动化存取系统货位分配优化研究
文/冉文学 余丽艳
在整个物流行业发展进程中,因为物流活动的发生,空间和成本问题,我们需要对物流仓储系统进行全面的优化设计,来提高作业效率及空间利用率并且降低劳动力成本。多穿梭板自动化存取系统既具有空间利用率高、存储容量大等优点,又具有灵活性高和周转效率高的优越性,较其它存储系统具有更高的吸引力,是少品种、高密度、高柔性等动态货物存取的最佳选择之一。
一、国内外相关研究综述

多穿梭板自动化存取系统具有多重优点,是少品种、高密度、高柔性等动态货物存取的最佳选择之一
Anna Azzi和Daria Battini(2011)等人提出以穿梭车的行走时间来预测多穿梭车自动存储系统(拣选系统)的系统性能,为证明其方法的有效性,采用蒙特卡罗模拟将所构建的模型与传统方法进行了分析对比;Shin-Ming Guo和Tsai-Pei Liu(2010)研究了双穿梭板在系统中的使用,分析了不同存储分配问题对双梭系统性能的影响,以及在多通道存储环境下双梭系统的优势;Tzur M,Drezner E(2011)通过分析穿梭板及升降机的运行时间,建立货架内设备运输托盘物资的时间模型,应用启发式优化方法评估系统性能,得到穿梭板的最优分配策略;Carlo H J(2012)等人研究了两个共桅升降机的调度问题,提出了两种评估函数,以量化和描述这两个升降机的效率和相互影响,根据工作要求及等待时间,通过启发式函数进行作业的优化分配;Ekren BY、Heragu SS(2011)等人考虑了系统中穿梭板和提升机的数量配置的合理性问题;Lu Chen和Andre’Langevin(2010)等人针对货物存取过程中出现的时间交叉滞留和考虑货位充分利用等问题,提出行之有效的解决办法,将自动化立体仓库的货位分配和时间交叉等问题有效解决。
付晓峰(2015)等人对多模式自动化存取系统的设备调度和多台独立升降机的任务分配进行了研究;郭丽红(2013)对多层穿梭车系统中每层一台穿梭车和m层n台穿梭车两种形式的拣选优化问题进行了建模,并采用遗传算法和精确算法给模型进行仿真;宋宇博(2015)等人通过对自动化存取系
二、多穿梭板自动化存取系统及其运作模式
1.多穿梭板自动化存取系统
多穿梭板自动化存取系统是由高速穿梭板和垂直提升机、高层货架系统、输送系统以及“货到人”拣选站台等组成。该系统在同一层面上的轨道是相互连通的,不同轨道层面又通过垂直提升机来上下联通,穿梭板既可以通过同层面的轨道相互联通,也可以通过垂直升降机变更到不同的层面,由此实现系统的自动化存取作业。
2.运作模式及其优点
可以根据实际作业量的大小灵活调整穿梭板数量是多穿梭板自动化存取系统的优势。当系统出入库流量较小时,可在不同巷道的不同层之间共用一个穿梭板,以降低仓库的建设成本及后期设备的维护成本;若某局部系统出入库流量较大,则可根据需要在各巷道的各层配置相应数量的穿梭板,以满足系统出入库流量的需要。
三、多穿梭板自动化存取系统货位分配优化模型的构建
1.模型符号及说明(如表1)
2.模型描述
根据出入库队列的长度,可将多穿梭板自动化存取系统划分为多个指令周期,系统按照指令周期模式进行运作,单个指令周期内最多可以完成的存货操作和取货操作的货物单元都为 ,据此我们假设高层货架系统内有 台穿梭板( )。根据系统存取货物队列的相关情况,穿梭板可以进行单一任务式和复合式两种指令周期作业的方式,其中单一任务式是指穿梭板单次行程时只完成 个货物单元的存货或取货操作,而复合式是指穿梭板单次行程同时完成 个货物单元存货操作和 个货物单元取货操作。本文研究对象为复合式指令周期,以最小化指令周期内存取货物的时间距离为研究目标,通过对多穿梭板自动化存取系统货位分配进行建模。
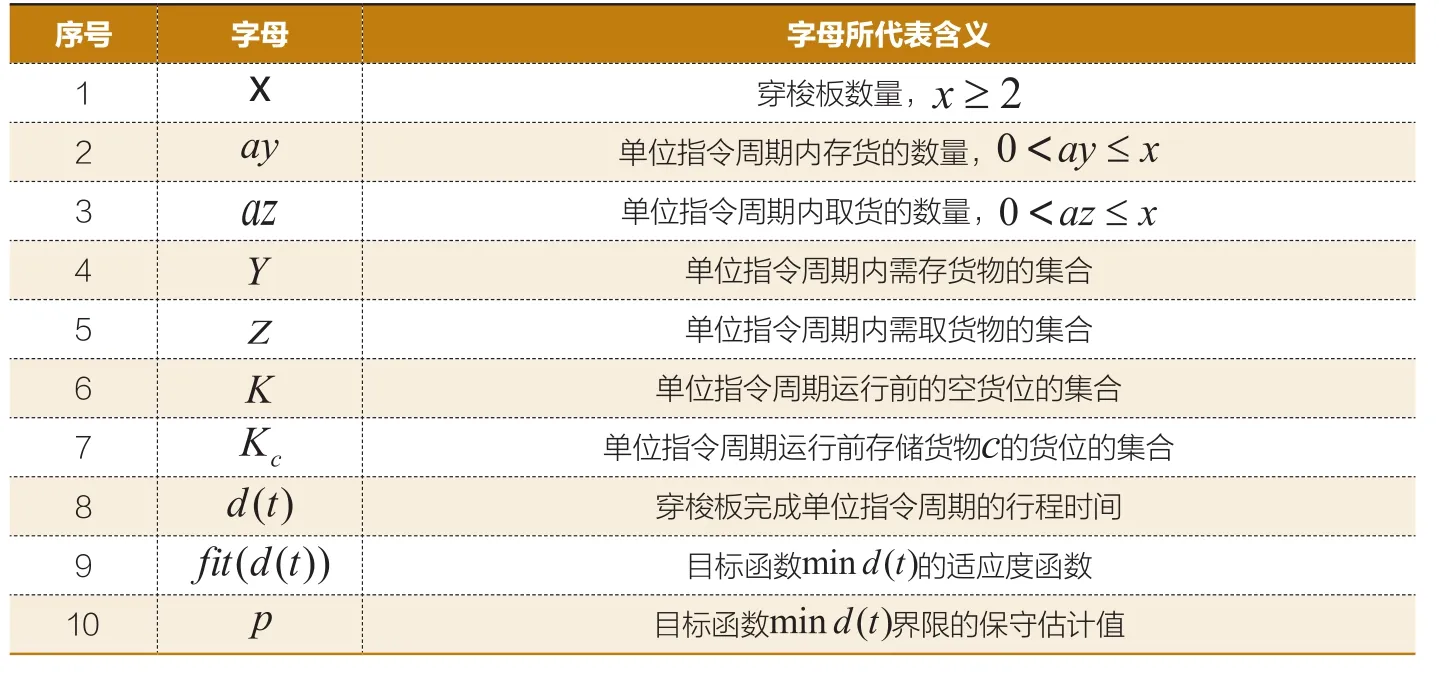
表1:符号说明表

图1:染色体编码设计

表2:不同优化方式仿真结果对比
为便于研究,在确定货位优化目标函数之前,本文假设:
(1)以单元货格式表示自动化立体仓库系统的存取方式。
(2)货架为矩形结构,并且出入库站台位于一侧货架。货架的长度及高度能够使穿梭板及提升机以最大速度在水平及垂直方向上行驶。
(3)系统中所有物料单元都是统一的。货架上的货位尺寸相同,并且任意一个物料单元都能够被存放在货架上的任意一个货位。
(4)各种货物的需求是已知、且固定的,货物之间无相关性。
决策变量假设如下:
,取1表示在一个任务指令周期内,货物 位于在货位 处,,否则取0;
一个任务指令周期内多穿梭板自统的动态货位分配进行研究,包括多指令周期的动态货位分配,以出入库的操作完成时间作为模型优化的整体目标,并设计单亲遗传算法对模型具体求解。
综观以上学者的研究成果,我们不难发现:现有对自动化仓储系统的研究主要集中在穿梭板和提升机运输环节,而关于货位分配优化的研究主要只考虑了货物间的相关性、货物的周转率以及货架稳定性等因素,对影响货位分配方案研究还很少。动化存取系统的货位分配可归为组合优化问题,由此可构建优化模型如下:
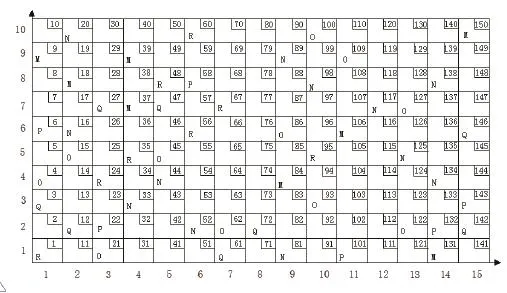
图2:货位初始分配图

图3:遗传算法寻优过程

约束(2)令一个空货位上存放一种物料;
约束(3)令一个空货位存放的物料种类小于等于1;
约束(4)表明只能从一个存有该物料的货位集合中获取所需的物料;
约束(5)意味着一个存货货位至多取一种所需的物料。
在穿梭板数量和货位规模变化的情况下,仍可用该模型对货位分配进行优化。总和为编码的长度。三穿梭板自动化存取系统一个任务指令周期内的货位选择,方案如图1所示,待取货物分别以A、B和C表示,为了满足存取货约束需保证从空货位片段中选取三个空货位,在存有A、B、C的货位片段中各选取一个货位, 本文选取{5、7、28}三个空货位进行存货,在7、13、3的编号货位中分别取出货物A、B、C。
(2)生成初始种群
考虑到本研究采取的编码结构取值约束的特殊性, 如果采取完全随机的方法生成初始种群,将会产生大量的不可行解,导致算法难以进行。为避免这种情况的发生,本文对于采用生成初始种群的随机方法需考虑分片段货位数量的限制,种群规模的大小选择从理论上来说越多越好, 但为方便迭代计算,方便后续遗传操作,本文取编码长度为2或4等的偶数倍表示种群规模。
(3)适应度函数和种群选择
在选择过程中,通常会用与求最优解的目标函数相关的适应度函数(fitness function),来分析评价这些染色体,然后再通过遗传算法来选择出较优的染色体。适应度函数的选择尤为重要,在遗传算法的操作开始就是依据适应度函数评价出来的染色体,如果适应度函数选择失误,那将会影响到整个遗传算法的收敛,同时最终结果也无法保证最优。
由上面构建的目标函数可知,本文解决的问题为目标函数为最小问题,则可设立如下的适应度函数:
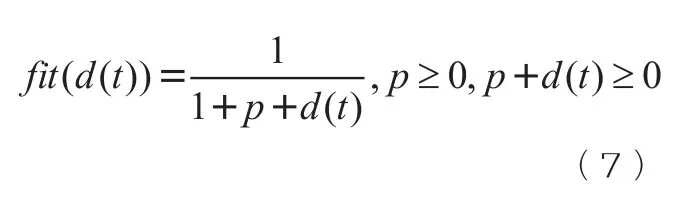
式中 为目标函数界限的保守估计值。
三、实例分析
1.实例概况
为了便于研究,本文设定某穿梭板自动化存取系统中的穿梭板数量为3,货架规格为1排15列10层,共150个货位,相邻两个货位之间的垂
3.遗传算法求解模型
(1)染色体编码设计
本文采用与待选货位集合映射的二进制编码方法对染色体进行编码设计,以“空货位+取货货位”的编码顺序进行排列,包括了上下两层,上层表示待选货位集合编号,下层表示是否选择对应货位的 0 - 1码值,任务周期内空货位的个数和待取货物的货位个数的直方向距离为0.6m,水平方向距离为0.75m,设穿梭板行驶的速度为6m/s,高速提升机的速度为2.5m/s。图2为系统货位的初始分布情况,方格右上角表示货位编号,存储的物料类型用方格内的字母表示,若方格内无字母,则表示该货位为空货位。一个指令周期内需要取出货物M、N和O;存入货物P、Q和R。
2.求解分析
在利用遗传算法迭代计算前,需设定如下参数:
提取指令周期内可访问到的所有货位的集合,即空货位和存储货物M、N、O 的货位集合, 按“空货位+取货货位”的顺序对染色体基本结构的形成进行排列;
采用0-1编码以形成个体种群,编码长度为100,种群规模为200;
取交叉率 ,变异率 ;
最大迭代数500;
适应度函数:

图3是遗传算法寻优的过程。种群平均适应度在遗传操作的开始较高,随后以较快速度下降,至200左右种群能被有效地控制在一定水平,种群质量有明显的提高,即可获得稳定解。
本文采用Matlab2013b对本文所构建的模型进行编程语言的设计,为验证模型的有效性,分析比较不同货位规模情况下,所构建模型对货位分配的优化程度,本文采用“最邻近”法(COL)与本文所构建的优化模型进行仿真对比,以复合指令任务完工时间为分析对象,得出货位分配优化程度的平均改进率,得到表2所示结果。
由表2中的结果,我们不难得出以下结论:
(1)本文构建的模型在穿梭板数量及货位规模相同的情况下,相比“最邻近”法,任务完工时间明显缩短,本文构建的优化模型优于“最邻近”法;
(2)系统的改进率,随着货位数的增加而增加,改进率增幅逐渐减小;
(3)运用本文所构建的模型对多穿梭板自动化存取系统进行货位分配优化,能够缩短货物的存取时间,存取效率有明显提高。
四、结束语
本文将多穿梭板自动化存取系统的货位分配问题归为组合优化问题,将最小化指令周期内存货、取货时间作为优化目标,针对不同穿梭板的数量以及货物的整体特征来建立数学模式,采用方法模型为遗传算法,对于多穿梭板自动化存取系统下的货位分配问题有一个有效的讨论,相对于以前的研究,本文更加注重高速穿梭板这一调度工具自身的特点,综合考虑多个因素对系统货位分配决策的影响,使模型具有通用性。最后将本文所构建的模型与传统的最邻近法货位分配策略进行模拟仿真,通过分析对比仿真结果,验证了模型的有效性,并对于企业或相关组织在此类问题上有一定指导作用。

