考虑能耗特性的岩桥型边坡动力失稳研究

邵 扬，李庆文，乔 兰，陈 璐，吴再海

(北京科技大学土木与资源工程学院，北京 100083)

随着露天开采技术和设备的不断发展，矿山数量和开采规模都不断增大，矿山由露天地表开采开始转向深凹开采，形成的边坡也就越来越高，岩质高边坡的稳定性问题受到了越来越多的学者的重视。在岩桥型滑坡方面，黄润秋等[1]指出很多高陡岩质滑坡的发生都伴随着其滑动面上岩桥段的突然滑移或破坏。黄润秋[2]还通过有限元数值模拟对边坡锁固段的应力路径进行了研究、分析。E.Eberhardt等[3]采用了数值模拟的方法，研究了多级锁固段控制下边坡的失稳机制。泮晓华等[4]对锁固型滑坡进行了系统的分类，首次提出潜在锁固型滑坡的预判方法。刘轶[5]在对锁固段钙质角砾岩的研究基础上引入了连续损伤结构模型，分析出锁固段的损伤本构方程。陈国庆等[6]采用强度折减法分析岩桥型岩质滑坡在渐进失稳过程中的动态安全系数，从而判断其稳定性。

边坡发生失稳破坏是一种复杂的地质灾害过程，由于内部结构的复杂性和组成边坡的岩石物质的不同，边坡失稳便会以不同的模式发生，对于不同的破坏模式就存在不同的滑动面[2]。对边坡破坏失稳模式的研究最早是从简单破坏模式开始的，Petterson等提出了边坡的单滑式圆弧破坏模式；E.Hoek归纳总结出岩质边坡的破坏模式主要有平面破坏模式、圆弧破坏模式、楔形破坏模式、倾倒破坏模式和崩塌破坏模式[7]。罗国煜等[8]提出了火成岩地区边坡变形破坏的15种破坏模式，不仅对已有的某些破坏模式作了进一步的细分，而且还增加了岩体松动破坏模式；曾宪明[9]对强膨胀页岩等特殊不良地质体的变形破坏形态和机理进行了试验研究，提出了胀裂破坏模式和流鼓破坏模式；目前针对大型岩桥型边坡失稳灾害的预测主要是基于力学理论来研究岩桥锁固作用的机理及坡体失稳的演化机制[10]，这就需要同时考虑多种因素的影响，分析相对繁琐，也加大了针对岩桥型边坡失稳灾害的预测难度。而本文重点从能量积聚、消耗的角度出发分析边坡岩桥段的承载能力，采用能量分析的方法会使分析更加简便和精确，因为能量是一种状态变量，不需要依靠它的路径。依据大量的原位节理、裂隙调查数据，可以将凹山露天矿边坡认定为岩桥型边坡，岩桥中主要起作用的能量可分为五个部分，即势能、爆破振动能、破碎耗能、摩擦耗能以及失稳动能。

1 岩桥型边坡界定

对于边坡稳定性，固有的节理、裂隙是最重要的影响因素，节理与岩桥的存在使岩体受力及破坏特征都发生质的变化，节理面使其强度削弱，岩桥则对强度做出贡献。岩桥指的是在边坡的失稳过程中应力相对集中并且提供关键承载作用的部位，其强度往往决定着边坡整体的稳定性。存在岩桥的边坡，其破坏过程是一个已有结构面开始拉裂或剪断岩桥导致破坏面贯通直至破坏的全过程，很多高陡岩质边坡的滑动带内都存在着岩桥段，将稳定性主要受岩桥段等关键结构体控制的边坡称之为岩桥型边坡。

本文是以凹山露天矿为工程背景，为了进一步描述边坡节理、裂隙的发展状态，在边坡北帮利用地质罗盘测量了306条节理、裂隙，并统一进行了分析处理，得优势节理裂隙组倾向约为ES120°和SW220°，矿区北帮的地层岩石主要为凝灰角砾岩。北帮边坡上部主要岩体为散体结构的凝灰岩，风化蚀变最为严重，岩体节理裂隙较为发育，因此其强度较低，下部岩体为较坚硬的闪长玢岩和安山岩，岩体相对较完整，其强度较高，因此边坡岩体具备储存上部岩体残余峰降能量的岩体结构，属于典型的下部岩桥型边坡。

2 能量分布分析

综合考虑矿区实际地质条件、边坡结构以及现场节理、裂隙的测量数据，绘制一个边坡岩桥段示意图，见图1。对于一个岩桥单元体，自身的储能和耗散能可以分为五部分，包括势能、爆破振动能、破碎耗能、摩擦耗能和失稳动能。

根据能量守恒定律，岩桥中分布的各部分能量满足式(1)。

EP+EV-EFra-EFri-EK=0

(1)

式中：EP为岩桥段及其上覆岩石的总势能；EV为由远处爆破引起的岩桥的振动能；EFra为岩桥的破碎耗能，根据断裂力学理论，破碎耗能包括产生岩块的新表面积能量以及产生的新的裂纹的能量；EFri为岩桥被吸收的能量破碎后结构面间的摩擦耗能；EK为失稳动能，它是块体失稳的能源。

为了消除尺度效应，本文将各部分能量表达成能量密度的形式，这样，式(1)可表达成式(2)。

(2)

式中，各个物理量分别表示式(1)中对应物理量的能量密度形式。

3 能量守恒分析

3.1 势能

势能主要指的是边坡单元体的重力势能，在分析势能的过程中，需要注意的是该势能既包括岩桥的重力势能，还包括其上覆岩石的重力势能，见图2。

图1 边坡岩桥段示意图

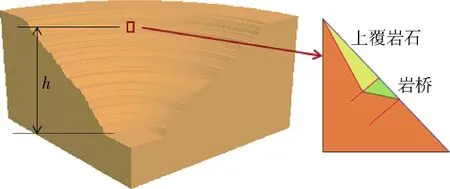
图2 岩桥势能示意图

重力势能计算见式(3)。

EP=mgh

(3)

式中：m为岩桥段及其上覆岩石的总质量；g为重力加速度；h为单元体距矿坑底部的高度。

因此，势能密度可表达为式(4)。

(4)

式中：VB为岩桥的体积；VC为上覆岩体的体积。

3.2 爆破振动能

爆破时，边坡面的振动速度能够通过爆破振速仪检测到，当监测点与爆破源的距离不同，振动波在边坡表面的传播和衰减程度会不同。可是，监测表面的振速并不能满足对岩桥中爆破振动能的研究，故国内外学者更倾向于使用数值模拟软件来预测振速。爆破振动载荷通常表征复杂，只采用传统的动力载荷模型进行分析，与实际的工程情况会有较大差异。李庆文[11]作了精确爆破振动分析，提出将整个爆破过程分为初期、中级、后期和末期四个阶段，归纳总结出式(5)～(7)。

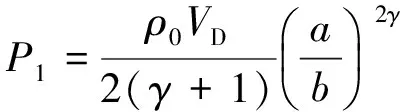
(5)

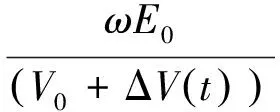
(6)

P3(t+dt)=Pe(t+dt)=

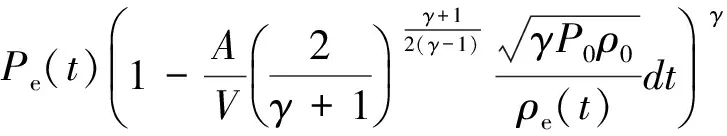
(7)

式中：P1为初始爆破压力，在不耦合装药的情况下其数值与爆破直径及药管直径的比例有关；a为药卷直径；b为炮孔直径；Vb为爆炸气体的速度；γ为爆炸气体的比热容比，一般取3；V0为炮孔的初始体积；A、B、R1、R2和ω均为爆破材料参数；E0炸药的初始能量。

通过Matlab程序对式(5)～(7)进行拟合分析，便可以得出爆破载荷作用的具体形式，见图3。

边坡三维模型建好后，结合精确爆破载荷理论、等效弹性边界理论等，速度场可被预测并计算爆破振动能，见式(8)。爆破振动能密度通过式(9)计算。

(8)

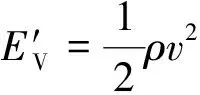
(9)

式中，v为通过FLAC3D数值模拟出来的速度。

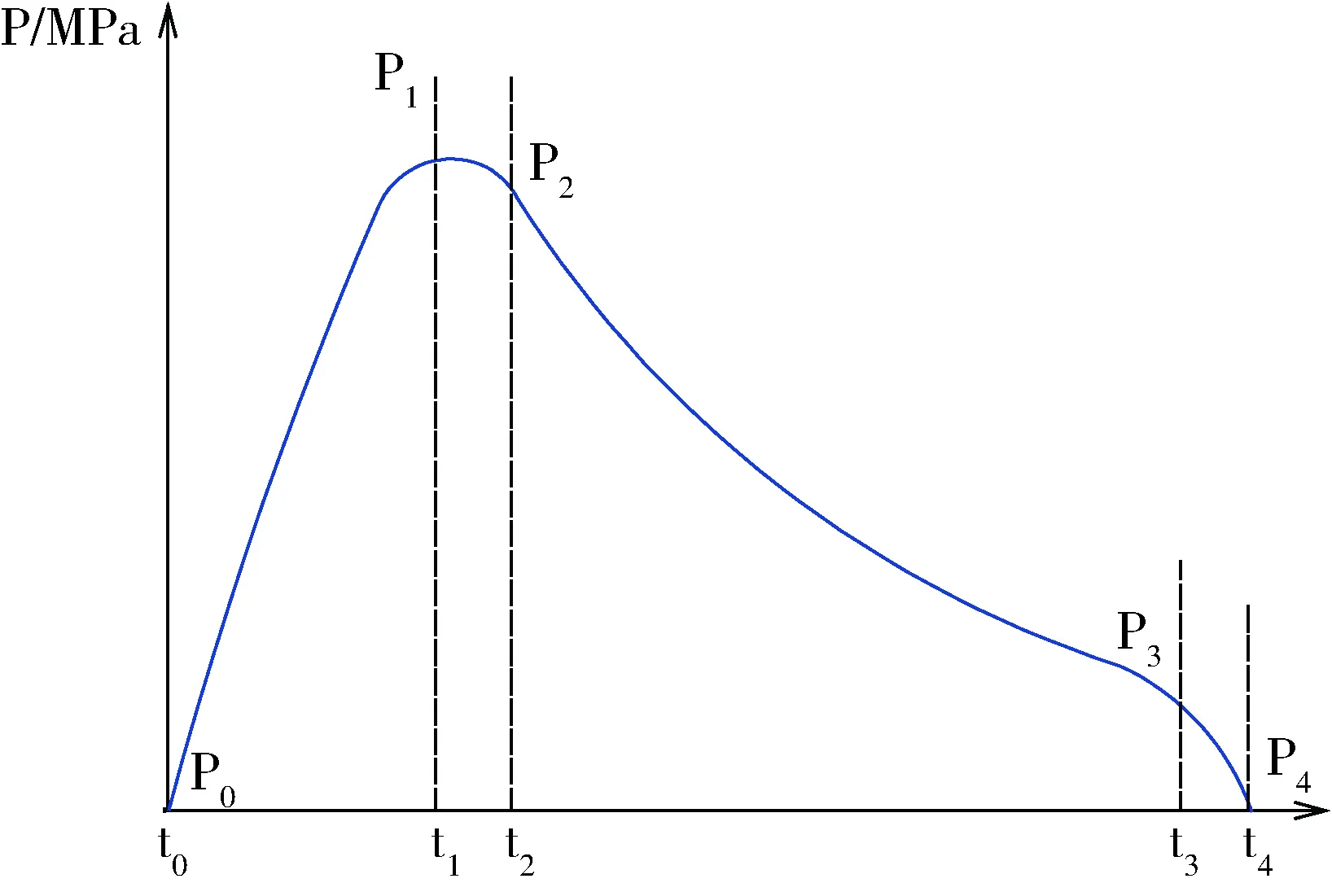
图3 精准爆破载荷模型

3.3 破碎耗能

根据断裂力学理论，当岩石受到爆破等冲击而发生破碎时，岩石内节理、裂隙的扩展以及新表面的产生都需要消耗部分能量，这部分能量就是破碎耗能。动态载荷导致岩石破碎会存在一个临界值，即只有输入的能量超过这一临界值，岩石才会发生破坏，反之岩石则不会破坏。破碎耗能以及发生破坏的临界值能够通过进行多组不同应变率下的SHPB试验来获取。破碎耗能通过式(10)计算[12]。

E0=Er+EK+Ere+EFra+Ed+Em

(10)

式中：E0为总输入能量，即撞击杆的初始输入动能；Er为撞击杆的回弹能，初始输入速度以及回弹速度可通过激光测速仪测得；EK为岩石破碎的动能，可通过高速摄像来确定；Ere为岩样的弹性应力波能，可通过公式计算得到；EFra为破碎耗能；Ed为撞击杆、入射杆和透射杆的塑性变形能；Em为其他残余的能量，如与声音和热有关的能量等。对于硬岩，最后两项可以忽略。

3.4 摩擦耗能

摩擦耗能指的是岩石吸能发生破坏后不同结构面之间相互运动所消耗的能量。它可以通过三轴压缩试验分析得到，应力-应变曲线及其曲线内区域划分见图4,不同区域代表着压缩试验中不同部分的能量：A区域指的是弹性状态下的塑性应变能Ee；在塑性状态下，A和B区域都表示塑性应变能Ep;C区域则表示弹性应变能Ee；当应力超过峰值强度就意味着岩样发生破坏，那么在之后的阶段，能量主要消耗在不同结构面间的摩擦上，即D部分指的就是摩擦耗能EFri。因此，摩擦耗能可用式(11)计算。

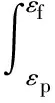
(11)

式中，f(x)指εf和εp之间的应力-应变曲线表达式。

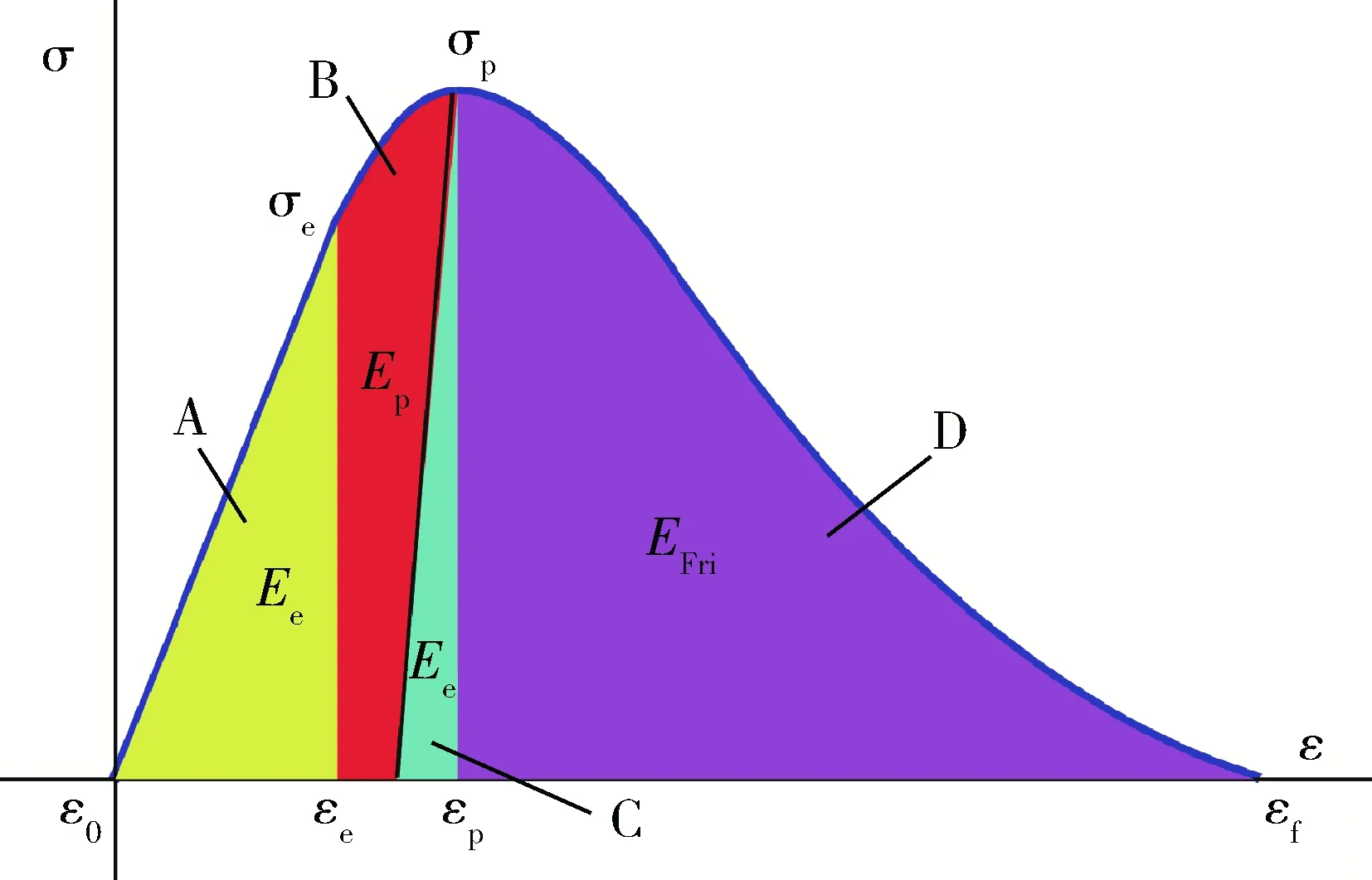
图4 三轴压缩试验及其能量划分图

3.5 失稳动能

失稳的动能是边坡失稳滑移的能量来源，它能使边坡岩体产生滑移甚至引发灾难。根据能量守恒，在分别计算出输入的能量和消耗的能量之后，残余的能量就是失稳动能，且失稳滑移速度可由式(12)确定。

(12)

式(12)得到的v可以用来判定边坡失稳滑移等级，这一理论、方法对于失稳的预测显得更加形象和准确。

4 凹山铁矿边坡稳定性分析

4.1 室内实验

凹山铁矿边坡岩桥段的构成主要是凝灰角砾岩，为了能得到岩块发生破坏的临界值及其破碎耗能，制备了20个凝灰角砾岩试样进行SHPB试验，试样直径50 mm，高25 mm。进行不同应变率下的SHPB试验，岩样会被压碎成不同的块度，应变率越高，岩样破坏得越完全。由图5可看出，进行SHPB试验之后，编号8、编号9、编号14和编号18的岩样并未发生破坏，对应的应变率分别是80 s-1、111 s-1、140 s-1和137 s-1。编号6和编号19的岩样存在裂纹，可以认为是刚好发生破坏，对应的应变率分别为155 s-1和146 s-1，平均应变率为150.5 s-1。因此，本文中确定的破坏临界应变率为150.5 s-1。

图5 SHPB试验后岩样图

同时，利用式(10)可以得到不同应变率下的岩石破碎耗能，见图6。

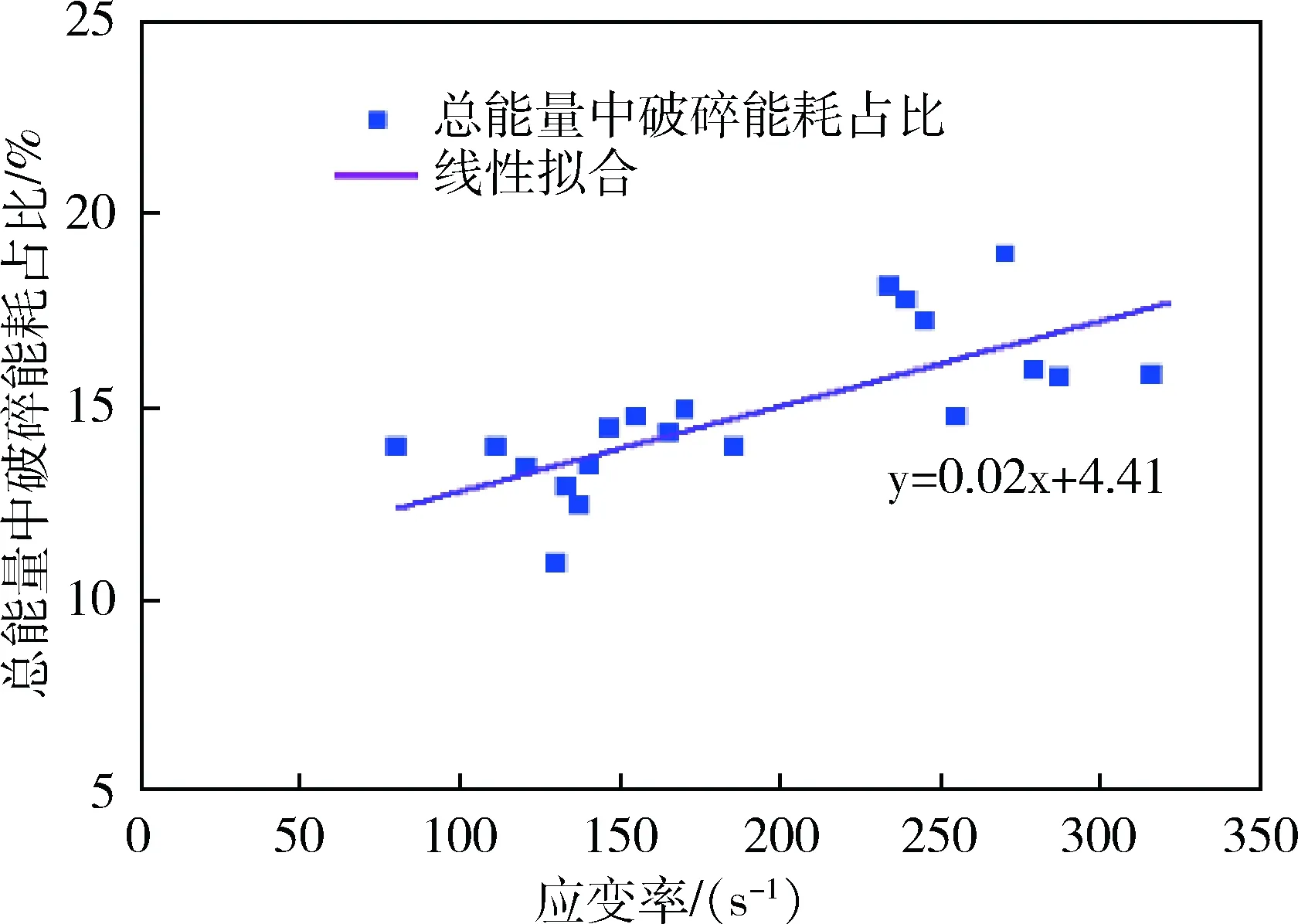
图6 破碎能耗与总能量比例关系图

为了确定块体的摩擦耗能，制备了3组共9个试样进行三轴压缩试验，实验前后的岩样见图7。摩擦耗能在总输入能量中的占比可以通过式(11)求得，结果见图8。

图7 三轴压缩试验前后岩样图

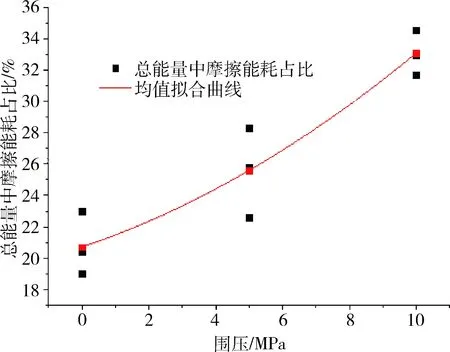
图8 摩擦能耗与总能量比例关系图

4.2 边坡数值模拟

依据实际的工程地质条件，使用MIDAS软件建立该边坡的三维模型并在FLAC3D中进行数值模拟。建立的三维地质模型沿x向1 100 m，沿y向1 100 m，沿z向620 m，总共得到了665 283个单元，123 752个节点。设定爆破区域为矿坑底部z方向175 m至200 m之间，影响半径30 m，爆破区域为77个单元。地层从上到下各层的力学参数见表1。

表1 岩石物理力学参数

爆破振速的峰值能体现出瞬时振动能的峰值，即爆破作用下岩桥瞬时吸收的最大能量，岩桥都存在一个自身无法承受的能量极限，引入振动能的峰值可以更科学有效地判断岩桥吸收的能量是否超出自身的能量承载极限。经过了138 912步计算之后，模拟出的速度-时间曲线见图9，在距离爆破区域300 m处的峰值速度为9.23 cm/s，在现场相同位置监测的速度-时间曲线见图10，对应的峰值速度为9.28 cm/s。

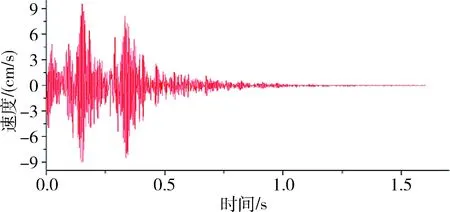
图9 FLAC3D预测的速度-时间曲线

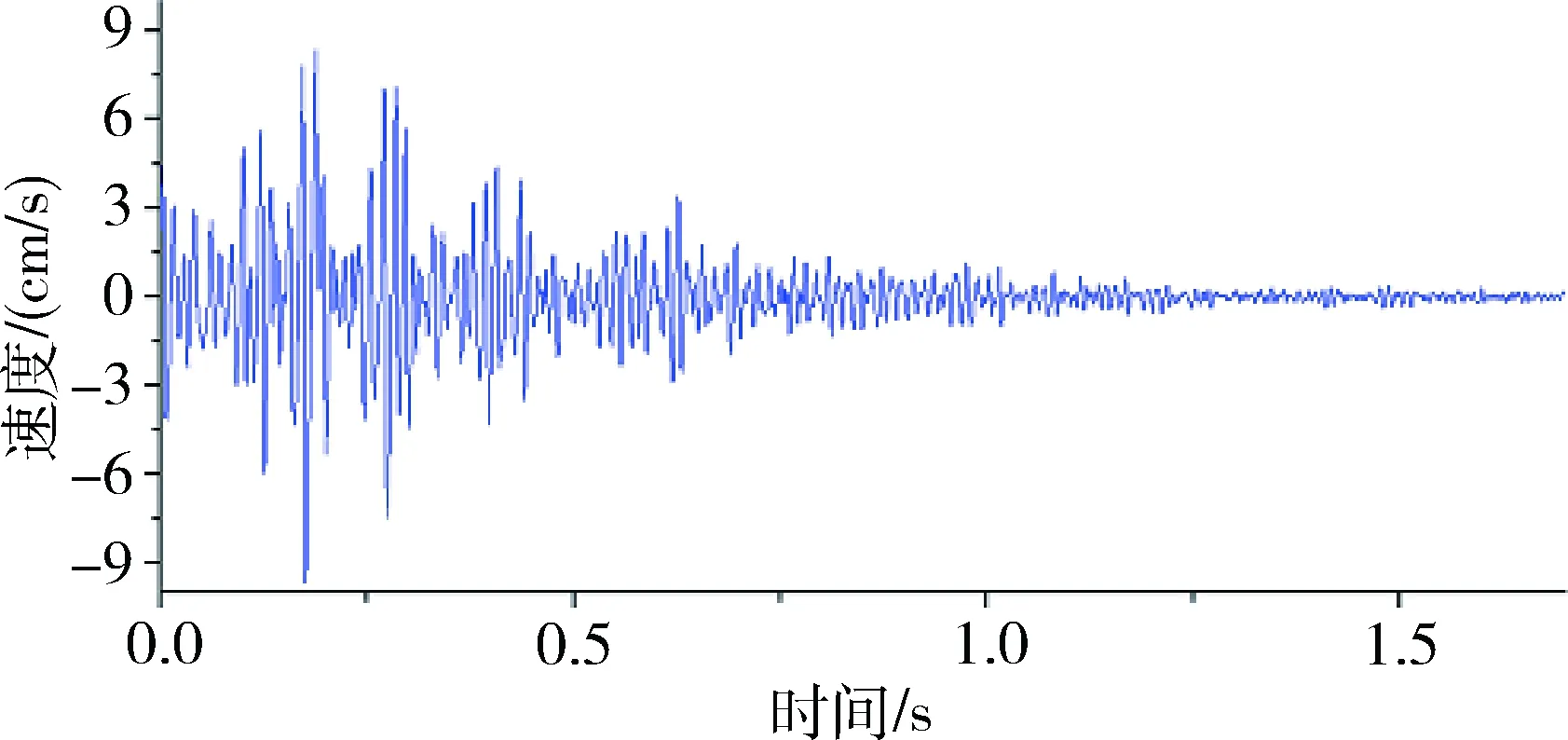
图10 现场监测的速度-时间曲线

由图9和图10可以看出，两条速度-时间曲线有着相似的峰值和衰减规律，证明了通过该模拟来预测爆破振动能是可行的。通过选用不同的动力响应时间，可以模拟出速度等值线图，见图11。

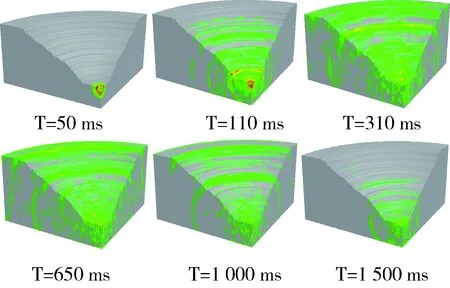
图11 不同计算时间下爆破振速区域等值线图

由图11可以看出，爆破振动波以球面波的形式从爆破中心向远处扩散，最强振动发生在4～5段爆破之间。本次模拟共设置了15个监测点，能够预测出距离爆破区域不同位置的峰值振动速度，见图12。

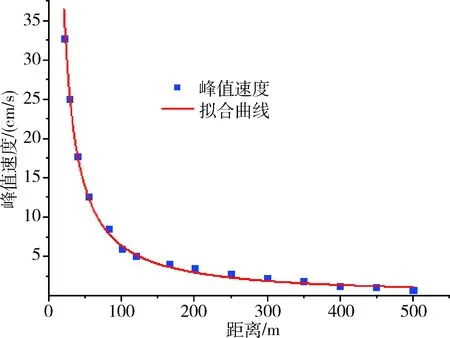
图12 预测的峰值振动速度及其拟合曲线

4.3 边坡稳定性安全判据

依据本文提到的方法计算出各部分能量之后，考虑到负荷岩石(包括岩桥段及其上覆岩石)与岩桥段的体积比率以及岩桥位置距离矿坑底部高度的不同，可提出一个边坡稳定性的安全判据，见图13。

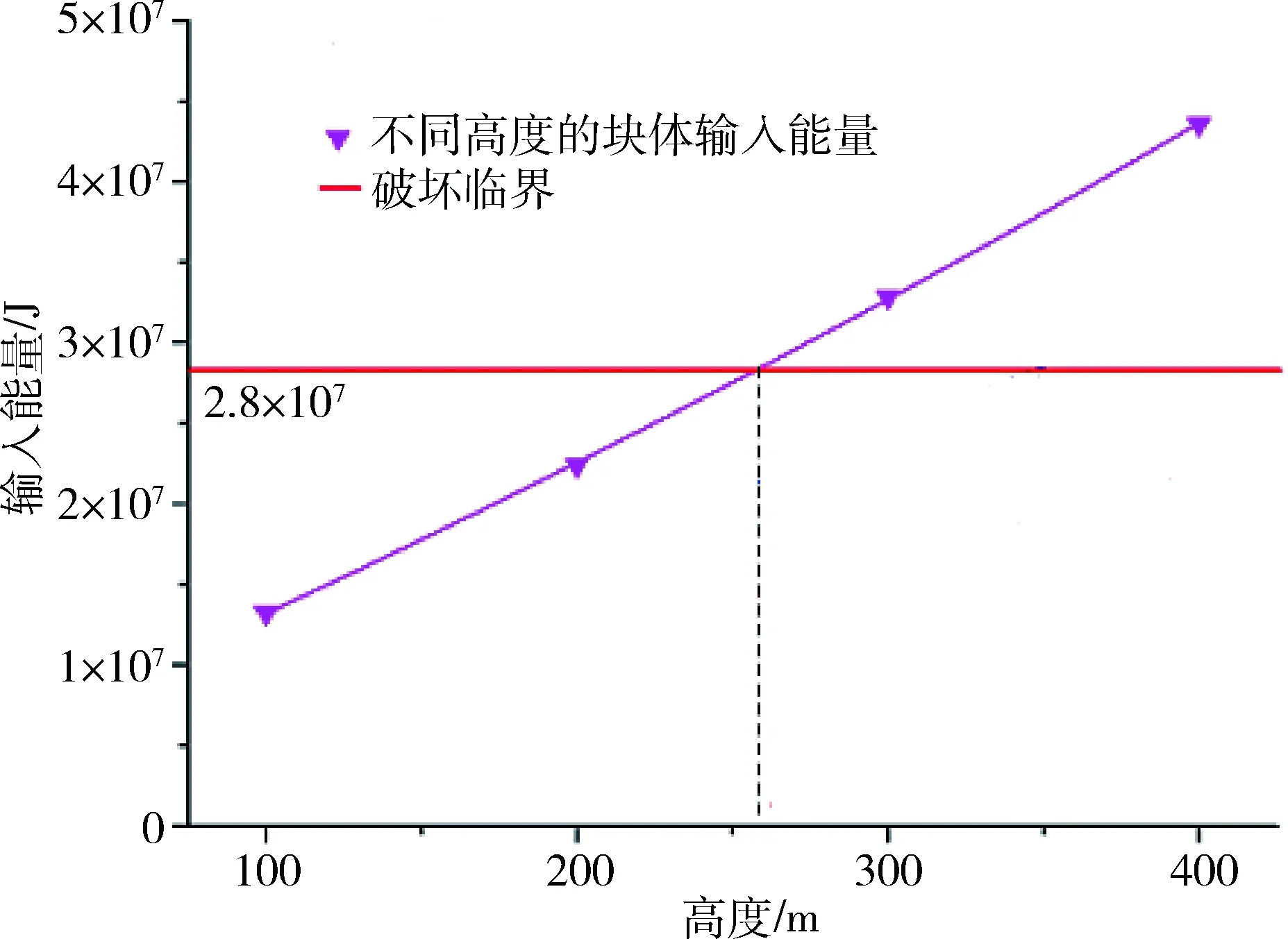
图13 边坡稳定性安全判据

当输入能量密度超过了由之前SHPB试验获取的发生破坏的临界能量密度时，岩桥就会发生破坏。由图13可看出，从能量的角度分析，爆破作业时距离矿坑底部约260 m高度的岩桥就会发生破坏。此外，从中剔除摩擦耗能的部分，边坡失稳滑移速度就能预测出来。以距坑底400 m高度的岩桥为例，块体会发生破坏的临界能量密度为2.8×107J，块体破坏之后剩余的能量密度约为1.6×107J，再剔除摩擦耗能密度1.1×107J，则失稳动能密度为0.5×107J。

5 结 论

1) 依据对现场大量节理、裂隙的调查研究，优势节理裂隙组的倾向为120°和220°。综合考虑实际的工程地质条件、边坡结构以及现场节理、裂隙的监测数据等，能够判断出凹山露天矿属于岩桥型边坡。

2) 根据能量守恒定律，岩桥中的能量可分解为势能、爆破振动能、摩擦耗能、破碎耗能以及失稳动能，每一部分的能量能够通过各自的理论或者室内实验来获取。

3) 对各部分能量密度详细分析之后，可以提出一个边坡稳定性的安全判据，边坡失稳体的滑移速度也能够计算出来，因此，能量分析法得到的判据对比传统的失稳判别方法显得更加精确和可视。

参考文献

[1] 黄润秋，许强.中国典型灾难性滑坡[M].北京:科学出版社，2008.

[2] 黄润秋.20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报,2007,26(3):433-454.

[3] EBERHARDT E,STEAD D，COGGAN J S,et al.Numerical analysis of initiation and progressive failure in natural rock slopes-the 1991Randa rockslide[J].International Journal of Rock Mechanics and Mining Sciences，2004，41(1):69-87.

[4] 泮晓华,薛雷,秦四清,等.潜在锁固型滑坡的类型、形成条件和预判方法研究[J].工程地质学报,2014,22(6):1159-1167.

[5] 刘轶.用“损伤”分析华蓥市溪口滑坡的形成机制[J].四川地质学报,1998(4):54-57.

[6] 陈国庆,黄润秋,石豫川,等.基于动态和整体强度折减法的边坡稳定性分析[J].岩石力学与工程学报,2014,33(2):243-256.

[7] HOEK E.Recent rock slopes stability research of the royal school of mines[C]∥2nd International Conference on Stability in Open Pit Mining.1972:23-46.

[8] 罗国煜，吴浩，王培清.岩坡优势面分析理论与方法[J].水文地质工程地质，1989(2):1-5.

[9] 曾宪明.特殊不良地质体变形破坏形态研究[R].广东省深基坑开挖工程学术研讨会，1996.

[10] 李正胜.锁固型边坡破坏演化机理及预警模型研究[D].北京:北京科技大学,2015.

[11] 李庆文.隧道等效弹性振动边界的建立及精确爆破振动分析[D].北京:北京科技大学，2010.

[12] 李夕兵，古德生.岩石冲击动力学[M].长沙:中南工业大学出版社，1994.