基于无单元法的混凝土结构水力劈裂数值分析模型
沈心哲 甘 磊,2 李舸航 刘泽涵
(1.河海大学 水利水电学院, 南京 210098; 2. 河海大学 水利部土石坝破坏机理与防控技术重点实验室,南京 210024)
迄今为止,世界上已经建成了许多高混凝土坝,其中不少高混凝土坝已达200 m级,甚至300 m级,这些高坝常年在高压水环境下运行,在高水压作用下大坝初始裂缝易起裂、扩展甚至贯穿,威胁坝体安全.
目前,国内外已有少量学者在混凝土结构水力劈裂试验及机理研究方面开展了研究.Brühwiler和Saouma[1-2]研究混凝土裂纹内水压对混凝土断裂性能和断裂过程区的影响,随后还研究了时间对断裂过程区内水压的影响.Slowik和Saouma[3]研究了动态荷载作用下混凝土裂缝张开速度对缝内水压分布的影响.徐世烺和王建敏[4]通过楔入式紧凑拉伸混凝土试件水力劈裂试验,研究静水作用下裂缝扩展长度及缝内水压力的分布规律.贾金生等[5]针对全级配混凝土圆筒试件开展单轴拉、压作用下的高压水劈裂试验,研究高水压对裂缝扩展的影响.甘磊[6]进行了无拉压应力、压应变条件下的单裂缝混凝土试件水力劈裂试验,针对I型裂缝测定裂缝扩展过程中的缝内水压分布.李宗利等[7]假定水力劈裂裂缝形态为半椭圆形,推导了任意时刻缝内水压分布微分方程式.黄云等[8]考虑裂缝内水压呈矩形、三角形等分布形式时,研究了缝内水压分布形式对裂缝扩展和坝体应力特征的影响.以上计算模型均仅考虑水流在裂缝面的劈裂作用.
混凝土结构水力劈裂数值模型不可避免地需要考虑缝内水流的作用效应,涉及到水流劈楔作用、水流行进及沿裂缝面的入渗行为对裂缝发展的影响.现在研究一般是将缝内水流的作用简化成作用于裂缝面的压力.陈胜宏[9]与董玉文[10]将缝内水压力视为上游全水头,分别研究了小湾拱坝坝踵的安全度和向家坝重力坝水力劈裂的特性.秦飞[11]采用了不同缝内水压分布形式分布,研究了不同水压分布形式对重力坝裂缝的稳定性的影响.进一步,方修君和金峰[12]在裂纹中的流体运动方面采用了立方定理,考虑了裂隙水流和开裂结构间的相互作用模拟了混凝土结构的开裂过程,并获得了开裂过程中水压的分布.沈振中[13]考虑了应力、渗流及损伤之间的相互影响,认为缝内水流具有法向与切向的双重作用,且缝内水流对于裂纹的扩展方向及裂纹长度的发展影响较大.林凯生和李宗利[14]建立了混凝土渗流-损伤耦合模型,研究了高孔隙水压对混凝土的损伤破坏的影响,Barani[15]采用非饱和渗流-损伤耦合模型,计算了紧凑楔入试件的水力劈裂特性,但未考虑裂缝扩展对混凝土损伤的影响.王克峰等[16-17]采用扩展有限元法,考虑了裂纹中的水压和裂纹宽度的耦合关系,对某典型重力坝的水力劈裂过程进行了数值模拟,但其裂纹内水压分布模型直接采用Brühwiler和Saouma[1-2]水力劈裂试验的成果,与实际情况存在较大差异.
目前,高水压作用下混凝土结构裂缝扩展数值模拟研究大多未考虑缝内水流与周围结构及裂缝介质的耦合作用,难以真实反映实际情况.本文将结合渗流力学和断裂力学理论,提出缝内水压力计算方法和水力劈裂裂缝扩展判据准则,基于无单元法建立了混凝土结构水力劈裂数值分析模型.
1 水力劈裂数值分析模型
1.1 裂缝不连续面的模拟
将不连续裂缝面作为一种界面来处理,在非连续面的两侧相应布置有两排距离很近的节点,如图1所示.这样处理,不但提高了不连续裂缝面的计算精度,而且这一对节点在非线性迭代过程中计算出的垂直于裂纹走向的距离可以作为本段裂缝的张开度,从而方便下一步计算裂隙内水压力的分布.
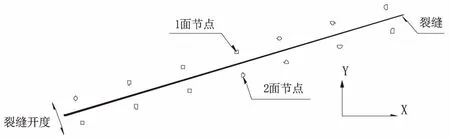
图1 裂缝节点布置示意图
1.2 缝内水压分布计算
针对粗糙裂缝问题,沿裂缝长度方向取若干微段体,将整条裂缝看成是由有限个单元组成的,当微段体的长度足够短时,裂缝就可简化成平行板之间的裂缝处理,则每个微段体的缝内水流流动方程为:
(1)
ui=-kiJi
(2)
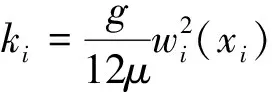
(3)
式中,qi第i个单元裂缝内的单宽流量;wi(xi)为第i个单元形心处的裂缝开度,ΔH为相邻单元的水头差;x为坐标;g为重力加速度;μ为水的运动粘滞系数;ui为裂缝中第i个单元平均水流速度;ki为第i个单元渗透系数;Ji为第i个单元平均水力坡降.
假定裂缝内无气体存在,且裂缝内的水流锋面以涌水模式向前,即裂缝被水充满,处于饱和状态,同时,考虑到混凝土为低渗透性孔隙介质,则
(4)
式中,q为沿裂缝长度的单宽流量;w为裂缝的张开度.
对非连续裂缝面迭代计算时,用来计算裂缝张开度的一对节点之间的距离相对于裂缝长度是微小的.故在考虑裂纹中的水流流动方程时,可以利用差分原理,对空间坐标采用差分形式处理,由式(4)可得:
(5)
将式(1)和式(5)联立求解,可得裂缝内水压力的差分形式为
(6)
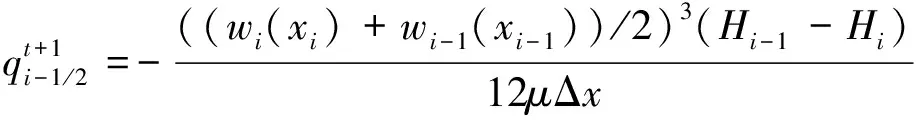
(7)
将裂缝处的节点概化为四边形的单元,如图2所示,根据式(5)~(7)对裂缝每个单元顺序进行联立求解,即可计算出此裂缝内水压分布.
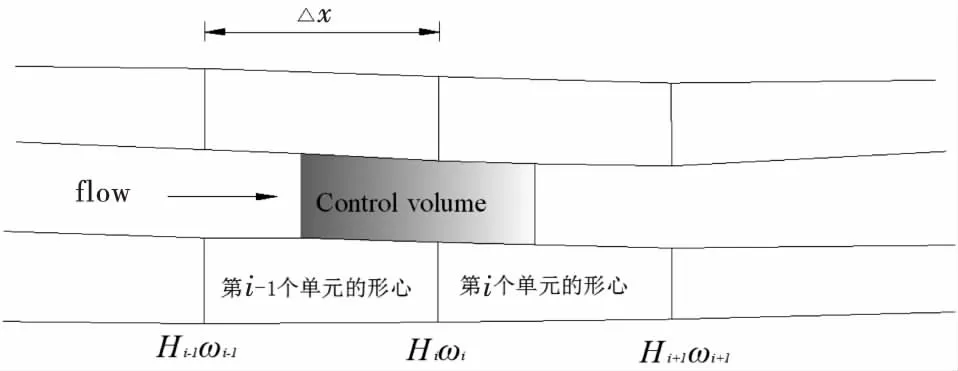
图2 裂缝内流体流动模型
本文采用迭代法求解缝内水压,使得本条裂缝其各节点的水压力之差最大值满足预设的精度要求即可.计算得出的缝内水压力分布作为面力荷载施加在相应的裂缝上,并转化为节点荷载作为混凝土体内节点的等效荷载.
1.3 水力劈裂裂缝扩展判据
计算渗透水压作用下复合型裂缝的应力强度因子,基于最大周应力准则,推导了不同应力状态下的水力劈裂裂缝开裂判据公式,推导过程详见文献[18].
当裂缝面法向正应力σn为拉应力时,裂缝为拉剪复合型裂缝,拉剪应力状态下水力劈裂裂缝开裂判据公式为
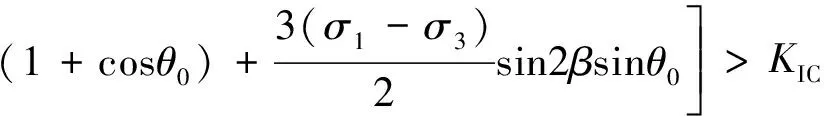
(8)
θ0=
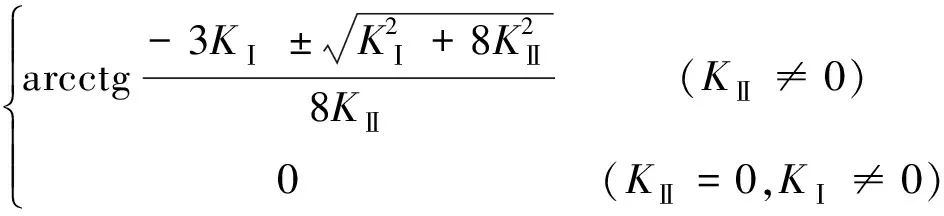
(9)
式中,σn为裂缝面的法向正应力;Kθ为裂缝尖端有效应力强度因子;2a为初始裂缝长度;θ0为开裂角;β为裂缝长轴方向与最大主应力夹角;P为作用于裂缝渗透水压;KⅠC为材料断裂韧度值;KⅠ,KⅡ分别为Ⅰ,Ⅱ型应力强度因子.
当裂缝面的法向正应力σn为压应力时,裂缝为压剪复合型裂缝,此时裂缝与拉剪复合型有截然不同的扩展失稳特性.由于裂纹面闭合压紧,裂缝要经历闭合压紧、剪切扩容过程.压剪应力状态下水力劈裂裂缝开裂判据公式为

(10)
式中,μ=tanφ+c/σn,φ为裂缝面的摩擦角,c为裂缝面的黏聚力.
1.4 数值实现
高水压下,缝内水压加剧了混凝土裂缝扩展、贯穿,导致混凝土结构渐进失稳破坏,而混凝土裂缝的劈裂扩展,导致裂缝混凝土的渗透特性变化,将改变渗流场的分布.这种渗流与混凝土裂缝断裂扩展的相互作用即为混凝土结构的渗流-断裂耦合作用.
渗流场对应力场及裂缝变形、断裂的耦合效应通常以渗透体积力和面力形式来体现,在无单元计算程序中,将渗透静水压力以面力形式计入节点荷载,将渗透体积力以体积力形式计入荷载,同时考虑水流的渗透压力不仅会对裂缝内壁产生法向的扩张效应,而且会对裂缝内壁产生切向拖拽力.
混凝土裂缝开度的改变、裂缝的扩展、贯穿形成新的裂缝会导致混凝土结构的渗流场发生改变,其裂缝内水压分布改变,导致应力场发生改变,而应力场对渗流场的影响可通过渗透系数变化来体现.而经典的Boit渗流耦合理论没有考虑应力引起的渗透系数的变化,不能满足动量守恒原理.本文在计算程序中补充了水力耦合方程
kn(σ,p)=k0e-α(σ-p)
(11)
式中,k0,kn(σ,p)分别为初始渗透系数和渗透系数;σ为正应力;p为渗透水压力;α为耦合系数.
2 算例验证
本文采用Slowik和Saouma楔形劈裂试验[3]的试件结构建立无单元数值模型进行分析计算,其试验装置示意图如图3所示.选取裂缝扩展速率较慢的试件wet10(速率为2 μm/s),其水压力恒定为0.21 MPa进行数值模拟,数值模型尺寸如图4(a)所示,计算区域均匀布置了3 600个节点,裂缝的尖端加密布置50个节点,计算采用一次基形式,数值分析模型如图4(b)所示,计算参数见表1.
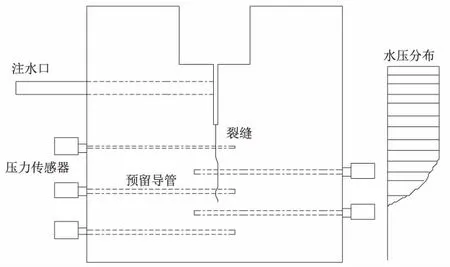
图3 楔形劈裂试验装置图
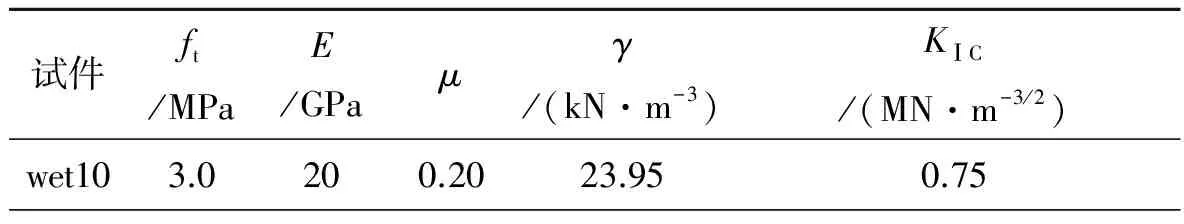
试件ft/MPaE/GPaμγ/(kN·m-3)KⅠC/(MN·m-3/2)wet103.0200.2023.950.75

图4 试件模型示意图(单位:mm)
图5为wet10工况下的荷载-裂缝口张开度的关系曲线.

图5 荷载与裂缝口开度的关系曲线
由图可知,本文数值模拟与试验结果及方修君数值计算结果非常吻合,尤其是在曲线到达峰值前阶段,本文数值结果和方修君数值计算结果较为一致,在峰值之后的加载后期计算结果均与试验结果相差较大.这主要是由于试验试件中预埋有测管和导线使得试验结果表现出一定的延性,而数值模拟时无法模拟这些因素对结果的影响.
数值计算得到wet10试件在加载中裂缝尖端随裂缝口张开度变化的关系曲线如图6所示.由图可知,本文数值模拟结果与Slowik[3]和方修君[17]的数值计算结果虽然在数值上存在一定偏差,但是其变化规律一致.通过结果比较可知,本文的数值分析模型和计算程序是正确的,成果是合理的.
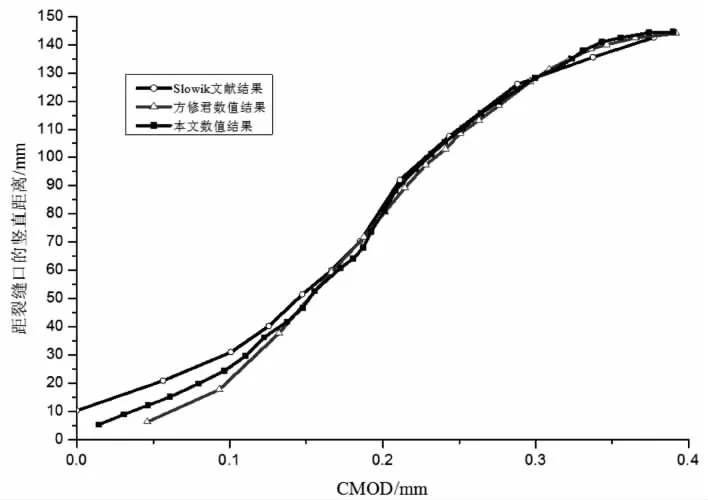
图6 裂缝扩展长度与裂缝口开度关系曲线
3 应用实例
将数值模型用于某一典型高混凝土重力坝,研究考虑流固耦合效应下混凝土重力坝裂缝承载特性.该坝高为216.5 m,坝顶宽18 m,坝底宽为158.16 m.上游坡面垂直,上游正常蓄水位210 m;下游坝坡坡比为1∶0.73,下游水位40 m.坝基高程设为0 m,坝顶高程为216.50 m.计算模型从坝踵往上游截取400 m,从坝趾处往下游截取400 m,竖直向往下截取400 m,坝体断面如图7所示.
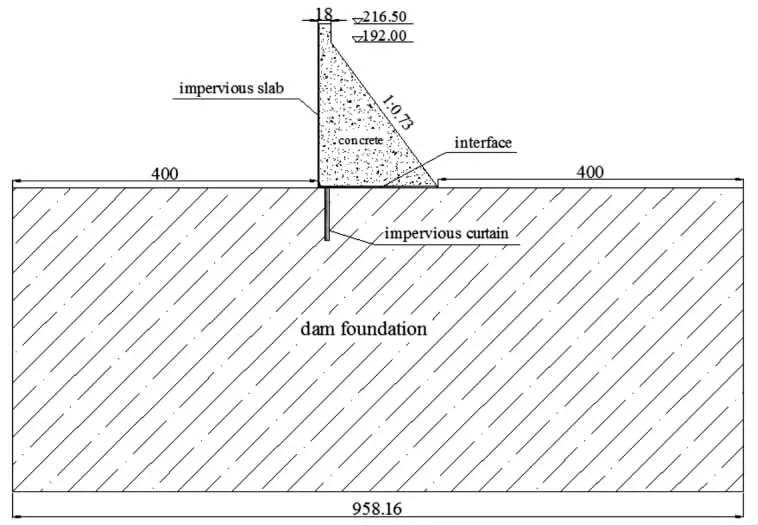
图7 坝体断面图 (单位:m)
坝体和坝基材料均考虑为各向同性的弹性材料,坝基与坝体界面,取0.5 m厚度,坝体和坝基材料分区示意图如图7所示,计算参数见表2.为了简化分析,不考虑坝体排水的影响.假定初始裂缝为水平裂缝,位于坝体上游面,初始裂缝距坝基面的距离5 m,初始裂缝宽度为0.1 mm,初始开裂步长为0.1 m.
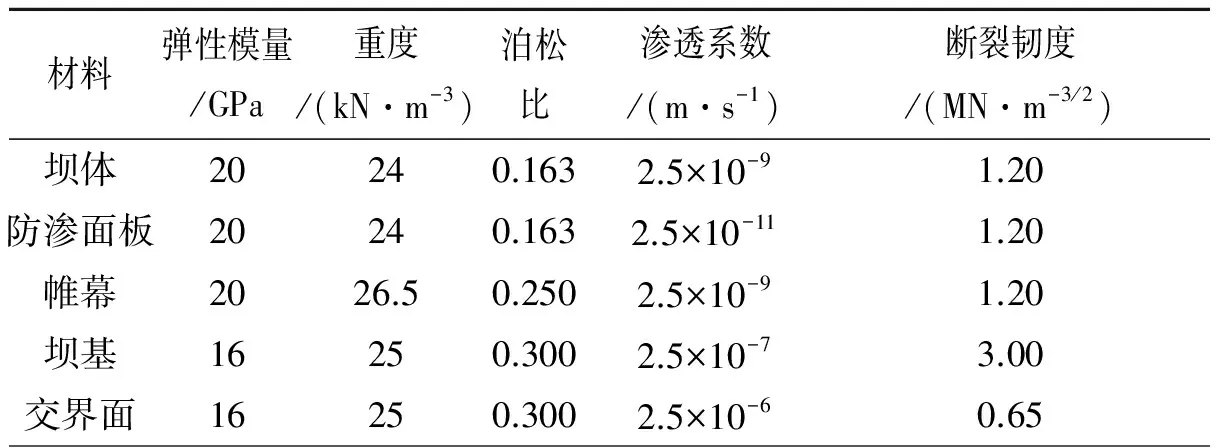
表2 重力坝材料参数表
计算模型初始节点布置如图8所示,共布置有5 855个节点,裂缝的尖端加密布置100个节点.
图8 重力坝模型图
考虑耦合作用下不同初始深度裂缝对应的临界上游水位(混凝土重力坝发生水力劈裂破坏对应的极限临界水位值)关系曲线如图9所示.从图9可以看出:初始裂缝深度越小,对应的临界上游水位值越大,即裂缝的起裂荷载越大,极限荷载受初始裂缝深度的影响较大;当初始裂缝深度小于0.6 m时,坝体的极限承载荷载呈幂指数下降,由临界上游水位由初始裂缝深度0.1 m对应的231.5 m下降至初始裂缝深度0.6 m对应的212.2 m,坝体的极限承载下降了8.3%;当初始裂缝深度大于0.6 m时,坝体的极限承载能力降低速率减缓,由临界上游水位由212.2 m(初始裂缝深度0.6 m)下降至205.0 m(初始裂缝深度2.0 m),坝体的极限承载能力近似呈直线下降,下降了3.5%.
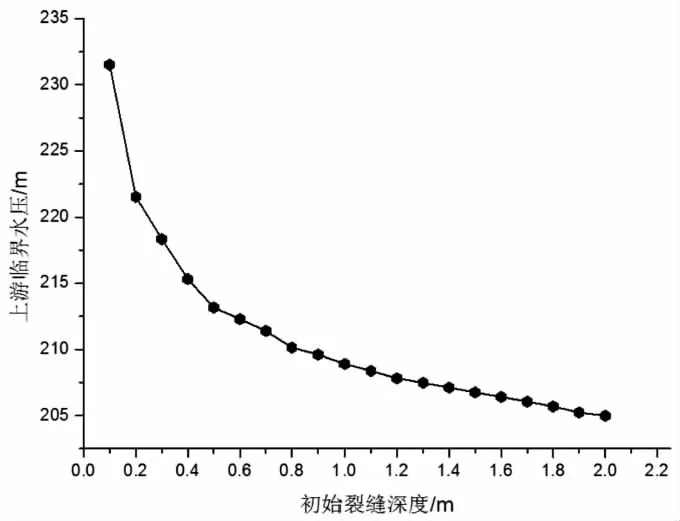
图9 临界上游水位-裂缝深度曲线
当初始裂缝深度为1.0 m,在不同缝内水压作用情况下,裂缝均是向坝体底部和下游侧开展,缝内水压力越大,裂缝开裂深度越大,当缝内水压力增大至2.05 MPa时,裂缝呈不稳定扩展趋势,裂缝一直扩展,直至坝体发生失稳破坏.计算成果符合一般规律,表明该数值分析模型可用于模拟高水压作用下的混凝土结构水力劈裂演化过程.
4 结 论
1)基于无单元法,结合渗流力学和断裂力学理论,提出缝内水压分布计算方法和水力劈裂裂缝扩展判据,考虑混凝土结构裂缝扩展过程中水流与混凝土结构的耦合作用,建立混凝土结构水力劈裂数值分析模型.
2)通过对混凝土楔形劈裂试验进行数值模型验证.结果表明:缝内水压变化规律和裂缝扩展规律与试验结果整体规律基本一致,说明本文所述数值模型是合理的.
3)采用数值模型,研究考虑流固耦合作用的高混凝土重力坝水力劈裂裂缝极限承载特性,结果表明:坝体极限抗裂荷载受初始裂缝深度的影响较大;当初始裂缝深度小于0.6 m时,坝体的极限承载荷载呈幂指数下降较快;当初始裂缝深度大于0.6 m时,坝体的极限承载能力降低速率较缓.模型计算结果符合一般规律,表明该数值模型具有一定应用价值.
参考文献:
[1] Brühwiler E, Saouma V E. Water Fracture Interaction in Concrete-part I:Fracture Properties [J]. ACI Materials Journal, 1995, 92(3):296- 303.
[2] Brühwiler E, Saouma V E. Water Frac Ture Interaction in Concrete-part II:Hydrostatic Pressure in Cracks [J]. ACI Materials Journal, 1995, 92( 4):383- 390.
[3] Slowik V, Saouma V E. Water Pressure in Propagating Concrete Cracks[J]. Journal of Structural Engineering, 2000, 126(2):235 - 242.
[4] 徐世烺,王建敏.水压作用下大坝混凝土裂缝扩展与双K断裂参数[J].土木工程学报,2009,42(2):119-125.
[5] 贾金生,汪 洋,冯 炜,等.重力坝高压水劈裂模拟方法与特高重力坝设计准则初步探讨[J].水利学报,2013,44(2):127-133.
[6] 甘 磊,沈振中,张 腾,等.混凝土结构水力劈裂试验装置研究及应用[J].水利与建筑工程学报,2015,13(4):130-136.
[7] 李宗利,任青文,王亚红.岩石与混凝土水力劈裂缝内水压分布的计算[J].水利学报,2005,36(6):656-661.
[8] 黄 云,金 峰,王光纶,等.高拱坝上游坝踵裂缝稳定性及其扩展[J].清华大学学报(自然科学版),2002,42(4):555-559.
[9] 陈胜宏,汪卫明,徐明毅,等.小湾高拱坝坝踵开裂的有限单元法分析[J].水利学报,2003,34(1):66-70.
[10] 董玉文,任青文.重力坝水力劈裂分析的扩展有限元法[J].水利学报,2011,42(11):1361-1367.
[11] 秦 飞,李 英.水压作用下裂纹的边界元分析[J].工程力学,2003(S1):304-307.
[12] 方修君,金 峰.裂隙水流与混凝土开裂相互作用的耦合模型[J].水利学报,2007,38(12):1466-1474.
[13] 沈振中,张 鑫,孙粤琳.岩体水力劈裂的应力-渗流-损伤耦合模型研究[J].计算力学学报,2009,26(4):523-528.
[14] 林凯生,李宗利.高孔隙水压作用下混凝土渗流-损伤耦合模型[J].水利水运工程学报,2010(2):51-55.
[15] Barani O R, Majidaie S, Mosallanejad M. Numerical Modeling of Water Pressure in Propagating Concrete Cracks[J]. Journal of Engineering Mechanics, 2016, 142(4):1-8.
[16] 王克峰,章 青,夏晓舟.考虑流固耦合效应的重力坝水力劈裂模拟[J].应用数学和力学,2015,36(9):970-980.
[17] Wang Kefeng, Zhang Qing, Xia Xiaozhou, et al. Analysis of Hydraulic Fracturing in Concrete Dam Considering Fluid-structure Interaction Using XFEM-FVM Model[J]. Engineering Failure Analysis.2015, 57(1):399-412.
[18] 甘 磊.水工混凝土结构水力劈裂试验及数值模拟[D].南京:河海大学,2013.

