基于MSC. Marc软件二次开发的岩土流变分析

冉 蠡 程 琳，2 杨 杰 仝 飞 陈诗怡

(1. 西安理工大学 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048；2. 河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；3. 福州大学至诚学院，福建 福州 350002)

流变在混凝土中一般被称为徐变，在岩石力学中一般被称为蠕变，均表示变形随时间发生变化[1]．对流变的分析，目前主要是采用流变模型．由于混凝土的力学性质(包括徐变性质在内)与材料的龄期有关，当混凝土的龄期较小时，材料受力后徐变发展得很快，只有当它的龄期达到相当大的时候(如1年以上)，徐变的发展才可以近似地认为与龄期无关，所以在建立混凝土的徐变理论时，应该考虑材料龄期的影响．混凝土的流变，可用专门的理论来分析，也可采用元件流变模型来分析．对于岩石的蠕变，则一般用元件流变模型[2]来模拟．图1是典型的岩石蠕变过程线，由图可知，岩石的蠕变可分为3个阶段.第1阶段(a-b)，减速蠕变阶段：应变速率随时间增加而减小；第2阶段(b-c)，等速蠕变阶段：应变速率保持不变；第3阶段(c-d)，加速蠕变阶段：应变速率随时间增加而增加．

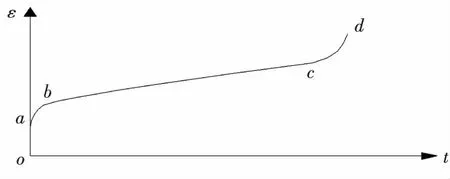
图1 岩石蠕变曲线

流变计算较为复杂，一般需借助相关的计算软件．在结构有限元分析的各种商业软件中，由于MSC. Marc软件[3-4]拥有多种高级非线性有限元求解器、充足的单元类型、丰富的材料库以及计算精度高等优点，本文以MSC. Marc软件为基础，进行二次开发，编制相关的程序，来实现流变计算．然后采用某抽水蓄能电站的面板堆石坝为算例，对开发的程序进行了验证．

1 流变问题的基本原理

设流变过程中结构的静力平衡方程为[5-6]

(1)

式中，B为应变矩阵；σ为应力；V为体积；f为外力．

采用小应变和小位移假设，即矩阵BT和坐标与时间无关．将上式对时间t求导，并根据应力应变转换关系进行推导，可以得到平衡方程的微分形式为

(2)

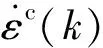
(3)

处理流变问题一般有显示方法和隐式方法两种．所谓的显式方法(初应力法)就是如式(3)所示蠕变项被完全处理成伪荷载，这样不需要重新组装求解刚度矩阵．所谓的隐式方法就是将式(3)右端第二项移到方程的左边，使刚度矩阵变成与流变应变相关的量，这样每个时间步都要重新组装刚度矩阵．

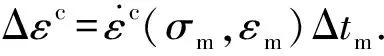
2 流变分析的伯格斯模型

在解决流变问题时，通常采用元件模型进行有限元分析[7]．元件模型是一种可模拟材料粘弹性性质的力学模型，其中伯格斯模型较为常用．

伯格斯模型是由一个Kelvin模型和一个Maxwell模型串联得到的[8]，如图2所示．

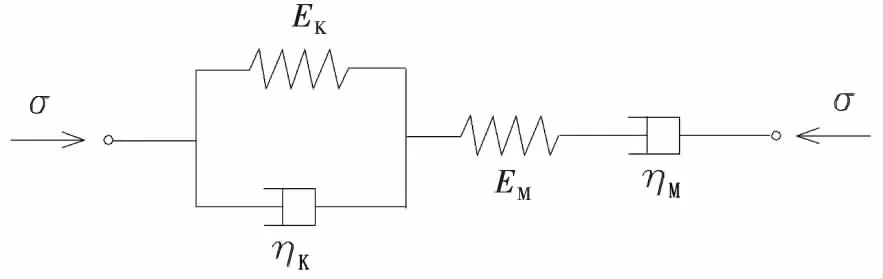
图2 伯格斯流变模型

则由Kelvin模型和Maxwell模型可推导出，在全量形式下，t0时刻到t=t0+Δt时段总流变应变为

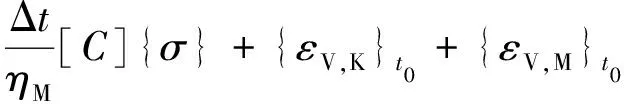
(4)

式中，EK为弹性模量；ηK为偏应力下粘性系数；ηM为静水应力下粘性系数；{εV，K}t0、{εV，Mt0}分别为t0时刻Kelvin模型与Maxwell模型的粘性应变；[C]为泊松比矩阵．

全量形式下，总流变应变增量，即减去初值({εV，K}t0+{εV，M}t0)后的值为

(5)

式(5)右边第一项是Kelvin模型对应的流变增量，第二项为Maxwell模型对应的流变增量．用偏应力和静水应力可分别表达为

(6)

(7)

式中，GK为剪切模量；BK为体积模量；Sij为偏应力；pm为平均应力．

3 MSC. Marc的流变分析与二次开发

3.1 MSC. Marc软件的对流变问题的处理

对于流变问题，当结构不存在塑性，即处于图1所示的蠕变的第一、二阶段时，会有以下3种情况：①仅采用Maxwell形式的模型；②仅采用Kelvin形式的模型(VISOELASTIIC)；③采用两种模型的组合．

MSC. Marc软件处理这种元件流变模型的常用思路见表1[9-11]．

表1 MSC. Marc流变分析二次开发快速参考

1)如果流变模型是Kelvin模型和Maxwell模型的组合(如伯格斯模型)，可采用以下方法：将总流变分为Kelvin模型部分和Maxwell模型部分，Kelvin模型部分的采用子程序CRIVIPS定义(只能定义偏应力产生的)，Maxwell部分采用CRPLAW定义或其它方法．如果还要考虑体积流变则采用VSWELL定义．(先将应力分为偏应力和平均应力，平均应力产生的体积流变用VSWELL定义，偏应力产生的对应于Maxwell部分的流变用②中的方法定义，偏应力产生的Kelvin形式的流变采用CRIVIPS定义．当流变应变的方程是采用应力全量的形式给出时，由于隐含着体积流变和偏应力流变形式相同，需将全量形式转化为偏应力和静水应力的分开形式进行开发)．

2)如果仅是Maxwell形式的模型，或是经验模型，指数模型等，(如三参数模型，经验流变模型，Maxwell模型)可以采用方案一中的显式或隐式方法．

3)如果是仅是Kelvin形式的模型(典型的如广义Kelvin模型)这时就直接采用CRIVIPS进行定义偏应力流变，如果还要考虑体积流变，则采用VSVELL定义．

4)当计算较为粗略时，可以直接采用CRPLAW子程序进行开发，计算中所需要的中间量(如上一步的Kelvin流变，Maxwell流变)均由用户自己定义．这时对于Kelvin模型和Maxwell模型的组合形式的模型而言，采用CRPLAW直接定义应变增量相当于将两种类型的模型产生的流变直接相加统一由用户定义，不再进行区分．

3.2 MSC.MARC软件的二次开发实现

根据上述分析，采用MSC. Marc软件实现伯格斯模型主要有两种方式：

1)采用全量形式下的表达式(5)直接利用CRPLAW子程序来实现；

2)根据式(6)和式(7),分别用CRPLAW子程序实现Maxwell偏应变流变分量，即两式的后半部分；用CRIVIPS子程序实现Kelvin偏应变流变分量，即两式的后前部分．

为保证模型精度，本文采用第二种方法进行二次开发．采用CRPLAW子程序定义显式粘塑性模型的非弹性应变率，CRIVIPS子程定义显式的广义Kelvin模型．考虑到结构同时产生的体积流变，则采用VSWELL子程序实现体积流变分量，并且认为体应力引起粘性变形的规律与应力偏量引起粘性变形的规律都和一般应力张量引起粘性变形的规律相同．

4 算 例

4.1 工程概况

某水利枢纽主要由上水库、输水系统、发电厂房及下水库等4部分组成．上水库布置于牢山寨北坡位置，挡水建筑物为主坝和副坝各1座，均为混凝土面板堆石坝，水库采用全库盆表面水平防渗型式，即库周采用钢筋混凝土面板防渗、库底采用土工膜防渗．上水库的主坝坝顶高程351 m，坝顶宽度10 m，坝顶长度1 110 m，最大坝高131 m(坝轴线处)，上游面坡比1∶1.4，下游面每20 m高设一宽2 m的马道，马道间坡比1∶1.35，其综合坡比约1∶1.45．

4.2 计算模型和参数

建立该抽水蓄能电站上水库面板堆石坝最大断面的二维平面有限元流变计算分析模型，如图3所示，有限元模型单元数278个，节点数307个，设置接触单元6个．不考虑流变时，堆石体的本构采用E-B模型来模拟，混凝土材料采用弹性本构关系．对岩石和混凝土采用伯格斯模型来计算分析结构的流变特性．

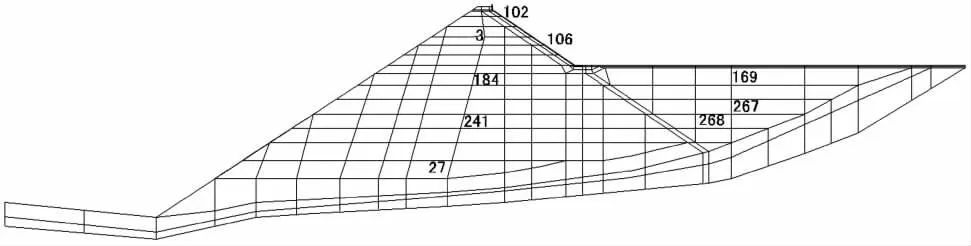
图3 坝体最大断面的有限元模型

国内外的试验和观测表明，堆坝的流变变形可以占到坝体瞬时变形的30%～50%．考虑大坝10年后，流变引起的变形占总沉降量的30%左右的情形，并参考其它类似工程的试验和计算结果拟定了坝体、回填区和面板材料的流变计算参数见表2．

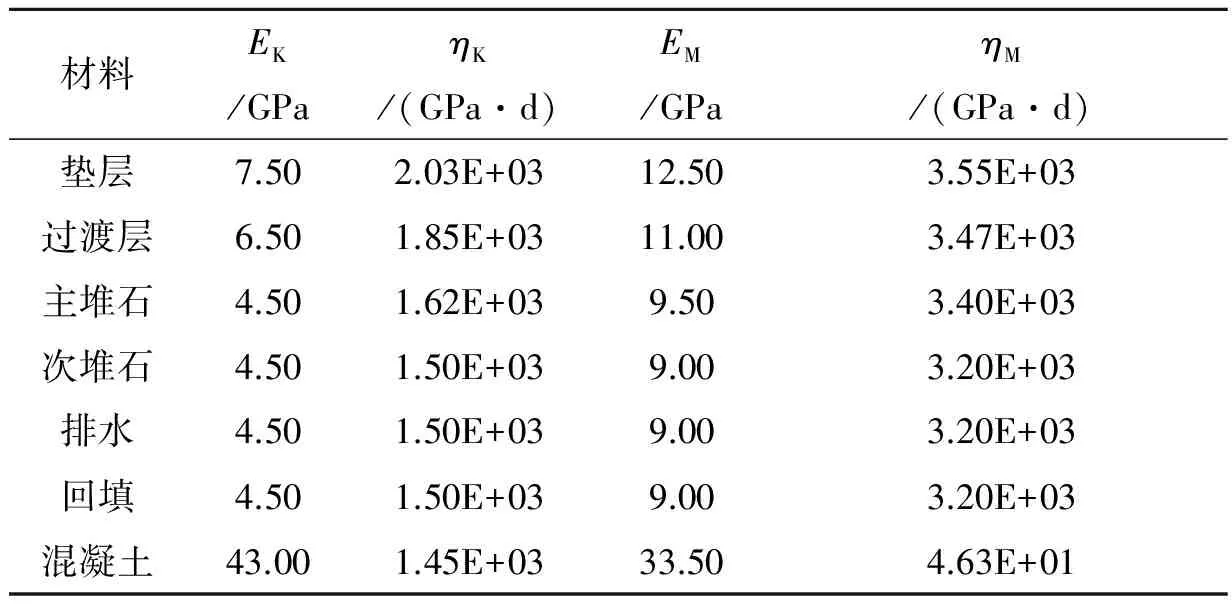
表2 伯格斯流变模型参数

4.3 计算成果

坝体部分结点在大坝运行10年后考虑和不考虑流变时的水平向位移和垂直向位移见表3．相应结点的位移历时曲线如图4～5所示．大坝蓄水期末和运行10年后考虑流变时的垂直位移分布如图6～7所示．水平位移向上游为正，向下游为负；垂直位移向上为正．由图表可知：考虑流变时大坝位移的分布规律与不考虑流变时基本相同．大坝运行10年后，垂直向位移最大值出现在坝体中部1/3～1/2坝高处．流变的效应使坝体水平向和垂直向位移的量都有所增加，但大部分结点后期的位移趋向平稳．

表3 考虑和不考虑流变时的位移比较

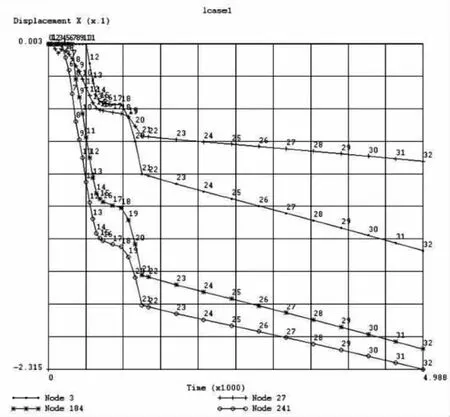
图4 坝体部分结点的水平位移历时曲线(单位：m)

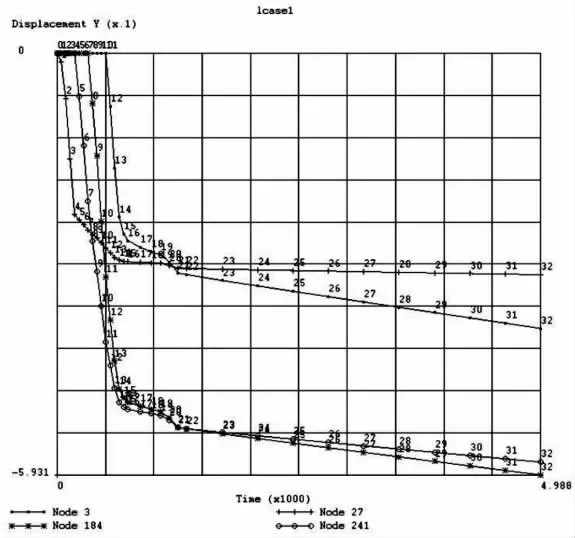
图5 坝体部分结点的垂直位移历时曲线(单位：m)

图6 蓄水期末垂直向位移(单位：m)

图7 大坝运行10年后考虑流变时的垂直向位移(单位：m)

坝体部分结点的最大主应力和最小主应力的历时曲线如图8所示．大应力以拉为正，压为负．由图可知：考虑流变效应时坝体主应力的分布规律与不考虑流变时基本相同．根据计算第一主应力的最小值为-2.73 MPa，第二主应力的最小值为-1.41 MPa．各向应力在后期都趋向平稳．

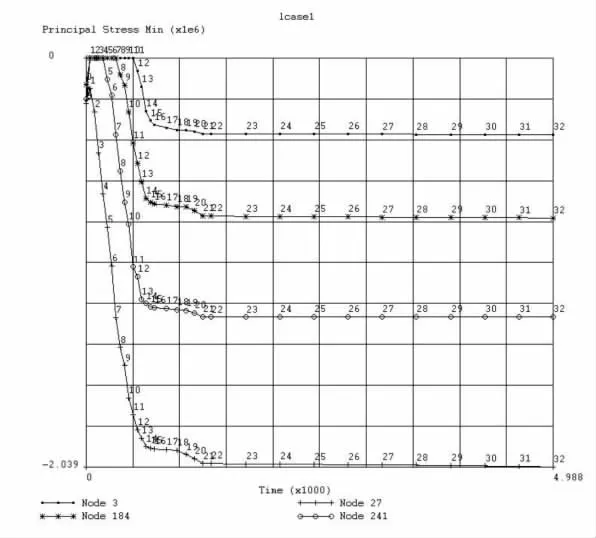
图8 坝体部分结点的最小主应力历时曲线(单位：MPa)

图9是主坝面板考虑流变和不考虑流变时的挠曲线的对比．考虑流变前后面板挠曲线的分布规律基本相同，都呈现出两端大中间小的特点．流变使面板法向位移有所增加，面板最大挠度由297 mm变为355 mm．根据面板应力的计算结果，不计流变时，主坝面板的最大法向压应力为1 805 kPa，考虑流变时大坝运行10年后面板最大的法向压应力为1 820 kPa，最大切向应力为1 810 kPa，较未考虑流变时的计算结果均有所增加．

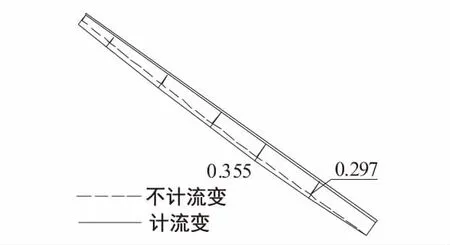
图9 考虑和不考虑流变情况下面板挠曲线的对比(单位：m)

由以上分析可知，在考虑堆石料与混凝土的流变情况时，其坝体与混凝土面板的应力较不考虑材料流变时均有所增加．表明堆石料与混凝土的流变对坝体与混凝土面板的变形特性具有较大的影响，堆石料与混凝土的流变使坝体与面板的变形增加，应力增大；而坝体变形的增加又会影响到混凝土面板应力变形情况，进而加大混凝土面板的应力值．

5 结 论

本文基于MSC. Marc软件进行二次开发，编制相关程序，采用伯格斯模型进行流变分析，再以某面板堆石坝为例，计算其流变情况下的应力变形情况．根据以上理论分析和工程实例的计算结果，可得以下结论：

1)考虑流变作用后的坝体位移和应力分布规律与未考虑流变时基本相同，位移和应力的量值在考虑流变后都有一定增加，但后期趋向平稳．

2)考虑流变作用后大坝各部位的位移和应力计算结果处于允许水平，面板和连接板应力和位移均有所增加，应加强相关结构部位的检查和维护．

3)在分析面板堆石坝的变形时考虑堆石料与混凝土的流变更能真实的反映出面板堆石坝的应力变形情况．对于高面板坝的变形分析，若不考虑流变，则会过小估计混凝土面板的应力变形，从而增大面板开裂风险．

4)本文开发程序的计算结果符合一般工程规律，证明二次开发是成功的，相关程序可以应用于实际工程问题．

参考文献：

[1] 刘 钰，黄耀英，唐腾飞，等．大坝混凝土分数阶徐变模型探讨[J]．长江科学院院报，2017，5(34)：1-5．

[2] 殷宗泽，等．土工原理[M]．北京：中国水利水电出版社，2007：368-141．

[3] 关天定，崔 杰，李亚东．基于MSC.Marc二次开发的土体等价非线性粘弹性模型[J]．土工基础，2011，25(6)：57-59．

[4] 屠立峰，包腾飞，陈 波．基于MSC.Marc软件的面板堆石坝加高的可行性研究[J]．三峡大学学报(自然科学版)，2015，37(5)：9-13．

[5] 佘亚鹏，王永明，卢继旺，等．200m级面板堆石坝流变分析[J]．水电能源科学，2010，4(28)：90-92+160．

[6] 王德信．面板堆石坝流变研究[D]．南京：河海大学，2003．

[7] 王瑞骏，李 阳，丁占峰．堆石料流变模型参数敏感性分析的正交试验法[J]．水利学报，2016，47(2)：245-252．

[8] 杨振伟，金爱兵，周 喻，等．伯格斯模型参数调试与岩石蠕变特性颗粒流分析[J]．岩土力学，2015，36(1)：240-248．

[9] 黄耀英，沈振中，吴中如．基于MSC．Marc二次开发进行粘弹性问题分析黑[J]．长江学院院报，2006，23(6)：95-98．

[10] 郭典塔，周翠英，石汉生，等．对Marc软件进行二次开发及其在地下结构中的应用[J]．地下空间与工程学报，2009，5(4)：786-791．

[11] 周 伟，常晓林．高混凝土面板堆石坝流变的三维有限元数值模拟[J]．岩土力学，2006，27(8)：1389-1393．