纵向数据分位回归模型的降维算法模拟研究

罗幼喜 ，李翰芳

（1.湖北工业大学a.理学院；b.产品质量工程研究院，武汉430068；2.华中师范大学 数学与统计学学院，武汉430079）

0 引言

近些年来，分位数回归[1]已经成为一种极为广泛的数据建模方法，它能全面刻画给定一组解释变量时响应变量的条件分布。由于分位数提供了比平均值更完整的关于响应变量的描述，分位回归也可以获得给定协变量时响应变量的整个条件分布，并在不同分位点处得到响应变量关于协变量效应的总体评估[2]。对于在实际生活中经常碰到的纵向数据，如临床试验、小组研究、流行病学调查以及计量经济中的面板数据等，Koenker[3]最先给出了相关讨论研究，并指出对于这类数据应该充分考虑到由于对相同个体测量而产生的个体变异性，以避免给参数估计带来的偏差。

目前关于纵向数据的分位回归模型多是使用非拉普拉斯分布（ALD）。这类方法的关键在于它将分位回归损失函数的最小化与基于ALD分布的似然函数最大化相等价关联，使得分位回归估计可以在似然函数的框架下进行。Koenker和Machado（1999）[4]首次提出了基于误差项为ALD分布的分位回归模型拟合优度检验。利用这个结论，Yu[5，6]提出了基于贝叶斯框架的分位回归方法。Luo等（2012）[7]通过ALD和分位数回归之间的联系，重点探索了包含随机效应的纵向数据贝叶斯分位回归模型的应用。然而，这些基于贝叶斯框架的分位回归法一方面对误差分布假设过于苛刻，不利于复杂数据分布的捕捉，另一方面后验分布密度函数较为复杂，只能通过MCMC算法求解，计算量较大。Koenker（2004）[3]考虑了含随机截距的纵向数据分位回归模型，通过在分位回归损失函数基础上对随机截距实施L1惩罚来估计固定效应参数，这种L1惩罚也称为Lasso[8]。由于L1惩罚的性质，Lasso能给予施加惩罚的参数连续收缩和自动变量选择，从而控制由大量随机截距引入带来的变异性。Zou（2006）[9]在Lasso基础上引入了一种自适应Lasso方法，该方法对回归系数使用自适应加权L1惩罚，与Lasso方法对所有系数实施相同的惩罚不同，自适应Lasso对较大系数选择较小权重，而对较小系数选择较大权重，所得估计具有oracle性质。最近，众多学者利用Lasso惩罚解决了线性和非线性分位回归模型中的变量选择问题，如Wang和Song（2011）[10]考虑了加速失效模型的自适应Lasso程序；Yang和Liu（2016）[11]对具有缺失协变量的线性模型，提供了在分位数回归检验函数基础上实施加权自适应Lasso惩罚的复合分位回归法等。但对于复杂纵向数据分位回归模型中的变量选择问题则研究还较少，本文拟将Lasso惩罚和自适应Lasso惩罚应用于纵向数据分位回归模型的变量选择问题中，并对方法进行模拟比较研究。

1 模型与方法

Koenker（2004）[3]考虑了含随机截距的纵向数据分位回归模型：

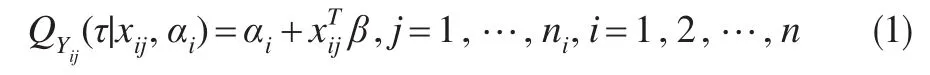
在检验损失函数基础上提出了对个体效应施加L1惩罚的分位回归方法，即极小化如下目标函数：

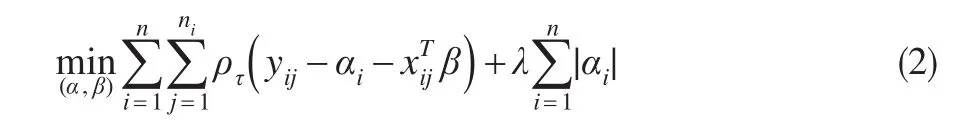
但上述方法是在固定模型中解释变量基础上进行讨论的，然而，在实际问题中，人们往往需要对初始建模时给定的一系列相关解释变量进行挑选，只保留较为重要的变量在模型之中，这样不仅能减少模型的冗余度，也可以提高模型的预测能力。

本文将对含多重随机效应的纵向数据分位回归模型考虑其自变量选择问题，记响应变量的条件τ分位函数如下：

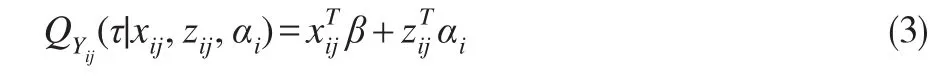
其中 β 为 k维 τ分位回归系数，αi，i=1，2，…，n为个体随机效应系数。与Koenker(2004)[3]不同的是，本文考虑对固定效应系数β分别实施Lasso和自适应Lasso的惩罚分位回归法，从而将非重要自变量权重系数压缩至0，起到变量选择的作用。即分别极小化：

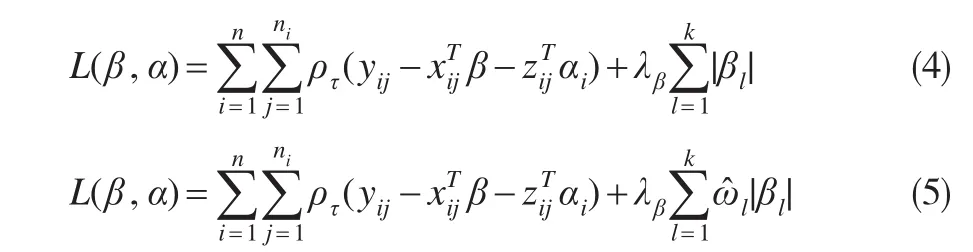
式（5）中相合估计，l=1，2，…，k。

式（4）所得估计称为Lasso惩罚分位回归估计，式（5）所得称为自适应Lasso惩罚分位回归估计。

事实上，Lasso方法也可以从贝叶斯角度获得一个很好的解释[8]，即在对回归系数 β进行先验假设时，可以根据高维数据稀疏性的特点，假设绝大多数回归系数值都集中在0左右，而少数非零系数则以较大概率出现，即先验为比正态分布更具有尖峰厚尾的条件拉普拉斯分布[12,13]。从而可以通过赋予回归系数条件拉普拉斯先验构造与Lasso方法等价的Bayesian Lasso法。

假设在给定 αi条件下 Yij，j=1，…，ni，i=1，…,n 相互独立且服从分布ALD(+σ，τ)，即：

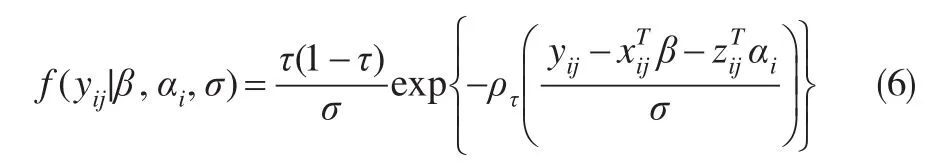
再对回归系数 βl，l=1，…，k赋予条件拉普拉斯先验信息：

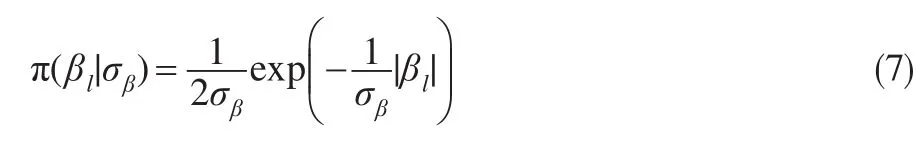
根据Bayes定理，可以推得回归系数β的后验密度函数：

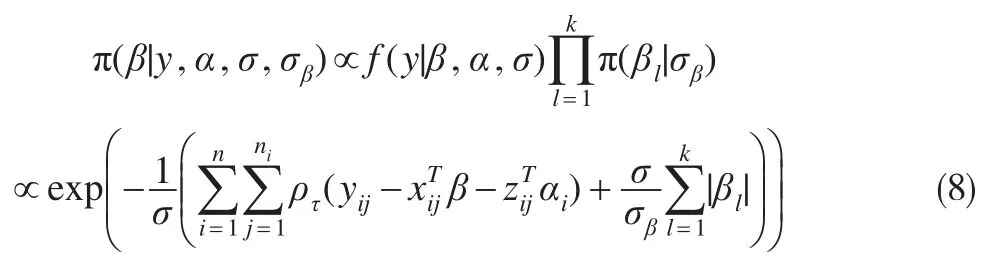
不难看出极大化式（8）以得到回归系数的贝叶斯估计，这等价于极小化式（9）：

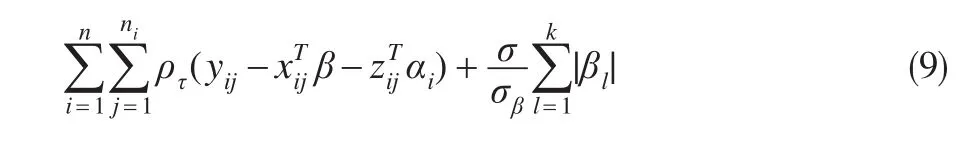
记 λ=则求解式（9）与求解式（4）是等价的，从而β本文获得了Lasso估计法在贝叶斯角度的一个解释，而不难看出其中的惩罚调整参数则与“信噪比”有关。

事实上，如果假定 βl， l=1，…，k有如下独立的条件Laplace先验：

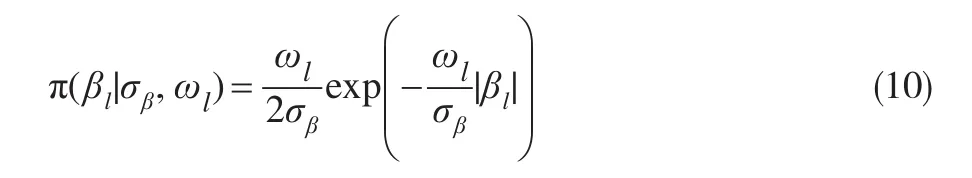
则类似可以得到与自适应Lasso惩罚分位回归估计相应的贝叶斯解释。

2 算法与惩罚参数选取准则

2.1 迭代算法

本文以Lasso惩罚分位回归估计为例来说明如何求解式（4），算法如下：

（1）给定初始值=0，i=1，2，…，n，求解一般Lasso分位回归估计可得=argminL(β，0)。

（2）按照下面两步交替迭代，m=0， 1，…

①=argminαL(，α)，此步可看成是调整残差为r(m)=yij-的一般分位回归估计求解问题。

②=argminβL(β，)，该步骤可以先将被解释变量yij调整为yij-，然后再求解普通的带Lasso惩罚的分位回归估计。

l体迭代过程中设定的误差最大容忍上限。

类似的，本文也可以利用上述迭代算法求解式（5）获得自适应Lasso分位回归估计，只需要将其中求解一般Lasso分位回归估计改为求解一般自适应Lasso分位回归估计即可，而自适应Lasso估计可以利用线性规划算法来解决[14]，考虑到线性规划算法可以很容易给出不同惩罚参数下的估计路径，从而本文只需根据给定的惩罚参数选取准则在每步迭代中挑选最优的参数值即可。而对于纵向数据一般分位回归估计，Koenker（2005）[2]早已给出了较为成熟的求解算法。值得一提的是，在自适应Lasso求解过程中，是未知的，本文可以取均值回归模型下的最小二乘估计绝对值的倒数来代替。

2.2 SIC参数调优准则

本文将采用SIC准则（Schwarz Information Criterion）来解决式（5）求解过程中的最优惩罚参数λβ选取问题，该准则既考虑到了尽量使模型拟合度高，又不至于让模型太复杂。SIC准则计算方法如下：

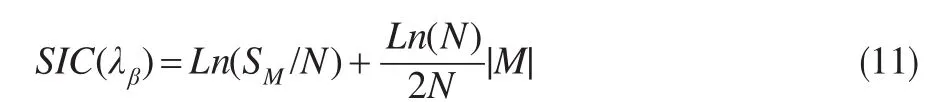
其中为检验函数残差和，衡量了模型的拟合度；是样本总量，| M |是模型中非零回归系数的总数，衡量了模型的简洁度。不难看到当λβ使得式（11）达到最小时，模型的拟合度和简洁度可以取得一个平衡。在具体的计算过程中，可以先确定一个搜索区间并将区间进行等份，然后在所有的等份点上利用交叉验证的办法得到最优的惩罚参数。

3 蒙特卡罗模拟比较

3.1 生成模型设定

为了检验本文提出的Lasso惩罚分位回归估计和自适应Lasso惩罚分位回归估计的效果，本文利用下面的纵向数据模型来模拟实际数据：

在上述生成数据模型中，本文设置各变量和参数如下：

（1）固定效应部分：8个自变量 X1，…，X8均来自N(0，1)分布，且任两个自变量之间的相关性随着其下标差绝对值增大而减少，具体的 ρXlXk=ρ|l-k|，且 ρ=0.5；

（2）随机效应部分：=(1，xij1，xij2，…，xij5) ，αi=

（3）随机误差部分：考虑随机误差εij分别来自N(0，1)，t(3)及Cauchy(0，1)分布，其中 t(3)，Cauchy(0，1)为厚尾分布，尤其是Cauchy(0，1)分布，容易产生绝对值较大的异常点，从而可以检验方法各种方法对异常点的稳健性。

（4）样本量大小：n=30， m=10；

（5）模型稀疏度：模型截距β0=0，考虑各个自变量前系数分别稠密、稀疏和高度稀疏三种情形，其中:

①稠密情形：

β=(0.85， 0.85， 0.85， 0.85， 0.85， 0.85， 0.85， 0.85)T

②稀疏情形：β=(3， 1.5， 0， 0， 2， 0， 0， 0)T

③高度稀疏情形：β=(5， 0， 0， 0， 0， 0， 0， 0)T

3.2 比较指标设定

对于蒙特卡罗模拟结果和进行比较的方法，本文作如下设定：

（1）相互比较的几种方法：①普通分位回归估计,记为QRE；②只考虑随机截距的Lasso惩罚分位回归估计，记为IQRE；③对所有固定效应系数带Lasso惩罚的分位回归估计，记为LQRE；④对所有固定效应系数带自适应Lasso惩罚的分位回归估计，记为ALQRE。

（2）各种估计法估计精确度衡量指标：

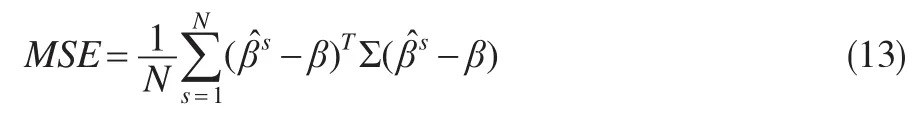
Σ=为第 s次模拟过程中 β 的系数估计值，另外本文还给出MSE在N次模拟中的标准差SD。

（3）各种估计方法对自变量选择准确度衡量指标：

易见，上述三个准确度衡量指标的取值范围均为[0，1]，其值越接近1准确度越高。且三个指标分别反映不同的侧面，其中Acc1反映估计方法保留重要自变量的准确性，Acc2反映估计方法排除非重要自变量的准确性，Acc为前两者的平均，反映估计方法的综合选择准确性。

3.3 比较结果分析

表1至表3给出了4种方法在不同模型下重复100次的模拟结果，其中LQRE和ALQRE两种方法在迭代过程中最大误差容忍上限值ε=10-4，所有方法对于系数的估计绝对值若小于10-6则计为估计值为0，也即该方法将对应的自变量排除在模型之外。另外，本文对高中低分位点均进行了模拟，考虑到不同分位点结果变化不大，故此处只对τ=0.5时的结果进行详细分析讨论。

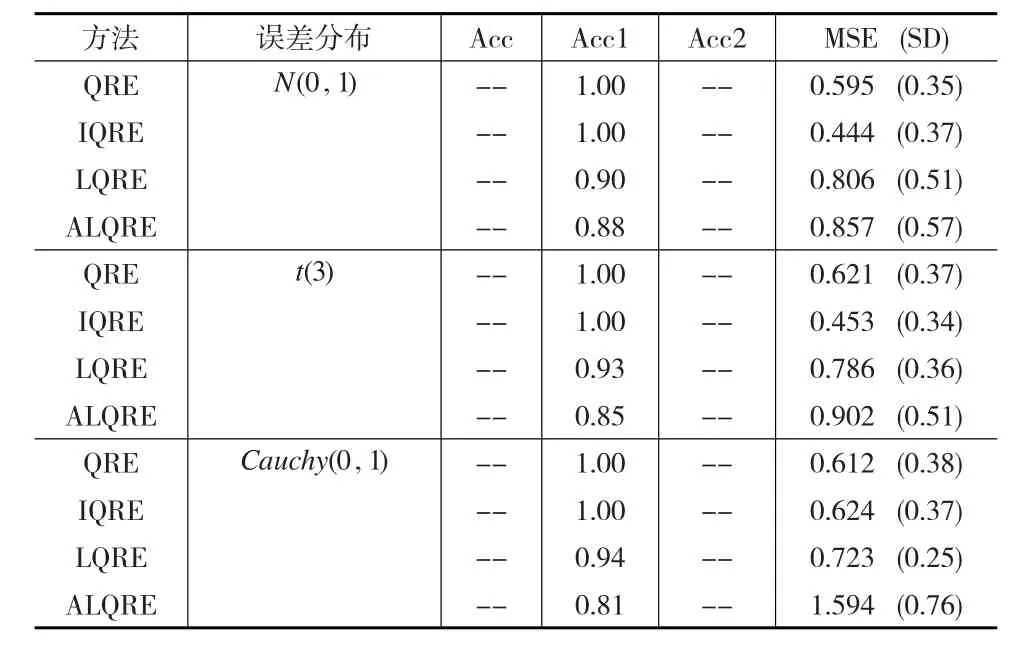
表1 稠密模型下四种方法参数估计结果

首先从表1稠密模型下的估计精度MSE来看，此时IQRE法和QRE法占优，尤其是IQRE法，在 N(0，1)和t(3)分布下MSE值均远远小于其他方法。这一点也不难理解，首先，由于本模型是稠密模型，所以从理论上来说，所有固定系数均不需要进行压缩，由于LQRE和ALQRE均对固定效应系数实施了压缩，从而导致其估计精度较没有压缩的IQRE估计和QRE估计有所降低。而对比LQRE和ALQRE，在各种分布下，LQRE均优于ALQRE，原因在于本模型中设定的所有固定效应系数均一致为0.85，而在ALQRE中，初始给定的权重估计很难完全一致，从而对每个变量的压缩程度也会有所不同，所以此时将所有系数压缩权重进行同等对待的LQRE法较ALQRE法占优，然而在实际问题中，这种所有解释变量系数均相等的情况是较为少见的。另外，由于本模型中所有变量均为重要解释变量，所以只需比较各方法的重要解释变量保留能力指数Acc1即可。从Acc1的值来看，显然完全没有进行变量挑选的QRE法和IQRE法始终将所有变量保留在模型之中，从而Acc1指数能够达到最大值1。而本文提出的LQRE和ALQRE法由于对变量进行了选择，故导致Acc1能力指数有所下降，但可以看到LQRE法能在各种分布下均保持90%以上的准确率，ALQRE法同样由于采用了不等权重压缩较LQRE法稍差，但其准确率也都在80%以上。另外总体上当分布逐渐由正态分布N(0，1)变为厚尾分布Cauchy(0，1)时，各种方法估计精度均有所下降，但下降幅度不大，尤其是本文的LQRE法，精度还略有提升，说明方法对异常点具有较强的稳健性。

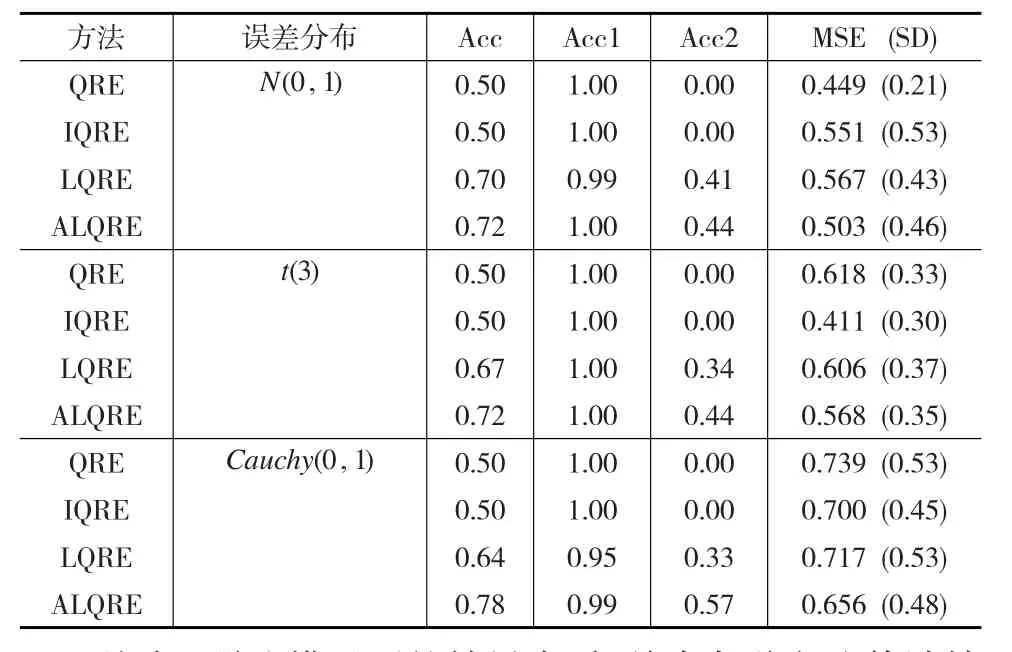
表2 稀疏模型下四种方法参数估计结果

从表2稀疏模型下的结果来看，首先各种方法估计精度MSE的值较之前的稠密模型更为接近了，其中在N(0，1)分布下QRE法最优，ALQRE法次优；t(3)分布下IQRE法最优，ALQRE法次优；Cauchy(0，1)分布下ALQRE法最优，IQRE法次优。所以综合来看，本文提出的ALQRE法能够在各种分布下均有较好的表现。再从模型选择能力指数上来看，虽然QRE和IQRE法的Acc1指数均为1，但Acc2指数均为0，也即它们没有进行任何变量选择，而是直接将所有变量纳入到模型之中。本文提出的LQRE和ALQRE法则显然既有重要变量选择功能，也有冗余变量剔除功能，尤其是ALQRE法，保留重要解释变量能力的Acc1指数均在0.99以上，且在3种分布下变量选择能力综合指数Acc均是最优的。对比稠密模型，这一点也不难理解，因为此时固定效应系数不再完全相等，故如果对其进行压缩惩罚，其惩罚权重也应该不同，LQRE法虽然进行了压缩，但其权重系数均一样，没有如同ALQRE法那样具有自适应性的功能。另外，当分布逐渐从N(0，1)变为厚尾分布Cauchy(0，1)时，虽然ALQRE估计精度MSE有所降低，但其变量选择能力几乎不受任何影响，综合能力指数Acc甚至还有提高。所以，对于这种在实际问题中可能最常见的模型，本文的ALQRE法无论是在估计精度上还是在变量选择能力上均有着极好的表现。

在实际问题中，在建模前往往存在大量的冗余自变量，即高度稀疏模型。从表3的模拟结果来看，LQRE法和ALQRE显然比传统的QRE和IQRE法在变量选择准确性以及系数估计精确性上都有较大优势，尤其是在变量选择准确性方面，传统方法几乎已经失效，而LQRE法和ALQRE都保持着80%以上的综合准确率，ALQRE更是保持85%以上的综合准确率。在MSE值方面，LQRE法和ALQRE也在各种误差分布下一直占优，尤其是在Cauchy(0，1)分布之下，ALQRE的MSE值仅有QRE和IQRE估计的一半，说明本文提出的ALQRE估计即使在高度稀疏模型下也对误差分布具有很强的稳健性。

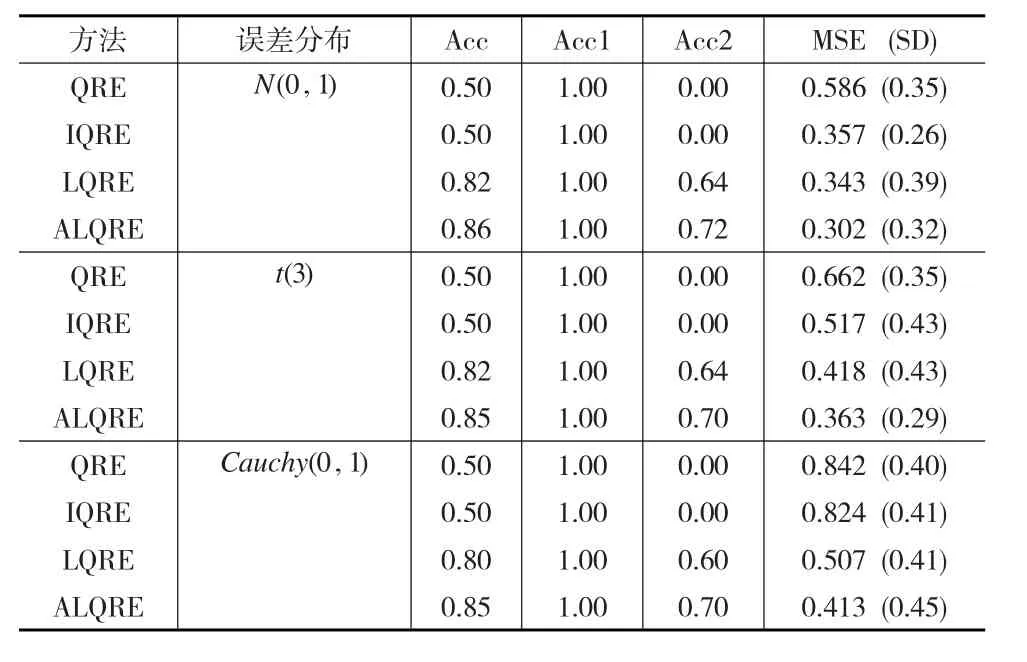
表3 高度稀疏模型下四种方法参数估计结果

4 结论

（1）本文将Lasso和自适应Lasso方法推广至含多重随机效应的纵向数据分位回归模型中来，不仅能够对模型中重要自变量进行自动选择，也能够对冗余变量进行自动剔除，极大地方便了实际工作者在数据初始建模过程中遇到的变量筛选问题。

（2）本文对两种方法设计的参数估计交替迭代算法充分利用了现有分位回归估计求解算法，快速有效地解决了目标函数优化问题。对于Lasso和自适应Lasso中惩罚参数选取这一难题，给出了能够平衡模型拟合效果和模型简洁度的最优惩罚参数选取准则，使得实际工作者不需要逐一试探惩罚参数的调节。

（3）通过在不同稀疏度情况下的模拟比较发现，当模型需要进行变量选择时，本文提出的两种方法不仅能够对于模型中存在的冗余变量进行一定程度的剔除，而且能够极为准确地保留模型中的重要解释变量。在模型高度稀疏时，两种惩罚分位回归法变量选择综合准确率达到80%以上，尤其是自适应Lasso惩罚法，不仅参数估计精度最高，而且变量选择准确度也最高，达到85%以上。所以该方法对于存在大量待筛选变量的情形尤为有效。

（4）通过在不同误差分布情况下的模拟比较发现，本文提出的两种方法对误差分布有较强的稳健性，尤其是在重要解释变量选择和冗余变量排除方面几乎不受到影响。

参考文献：

[1] Koenker R,Bassett,G.Regression Quantiles[J].Econometrica,1978,(46).

[2] Koenker R.Quantile Regression[M].New York：Cambridge University Press,2005.

[3] Koenker R.Quantile Regression for Longitudinal Data[J].Journal of Multivariate Analysis,2004，(91).

[4] Koenker R，Machado J.Goodness of Fit and Related Inference Pro⁃cesses for Quantile Regression[J].Journal of the American Statistical Association,1999,(94).

[5] Yu K,Moyeed R A.Bayesian Quantile Regression[J].Statistics and Probability Letters,2001,(54).

[6] Yu K，Stander J.Bayesian Analysis of a Tobit Quantile Regression Model[J].Journal of Economics,2007,(137).

[7] Luo Y,Lian H,Tian M.Bayesian Quantile Regression for Longitudi⁃nal Data Models[J].Journal of Statistical Computation and Simulation,2012，(82).

[8] Tibshirani R J.Regression Shrinkage and Selection via the Lasso[J].Journal of the Royal Statistical Society,Ser.B,1996,(58).

[9] Zou H.The Adaptive Lasso and Its Oracle Properties[J].Journal of the American Statistical Association,2006,(101).

[10] Wang X，Song L.Adaptive Lasso Variable Selection for the Acceler⁃ated Failure Models[J].Communication in Statistics-Theory and Methods,2011，(40).

[11] Yang H，Liu H.Penalized Weighted Composite Quantile Estima⁃tors With Missing Covariates[J].Statistical Papers,2016，57(1).

[12] Yuan M,Lin Y.Efficient Empirical Bayes Variable Selection and Es⁃imation in Linear Models[J].Journal of the American Statistical As⁃sociation,2005，(100).

[13] Park T，Casella G.The Bayesian Lasso[J].Journal of the American Statistical Association,2008，(103).

[14] Li Y，Zhu J.L1-norm Quantile Regressions[J].Journal of Computa⁃tional and Graphical Statistics,2008，(17).