一种软件浮动授权采购数量的估算方法

朱理化 黄 浩 方 伟

(中国航发控制系统研究所 江苏 无锡 214000)

0 引 言

浮动授权是一种计算机软件许可证管理方式。在这种方式下，软件有限数量的授权由授权管理服务器通过计算机网络共享给一个较大数量的用户群。目前，浮动授权得到了广泛使用，尤其适用于那些被众多用户间歇使用的昂贵软件。一方面，软件供应商通过浮动授权解决方案避免因侵权行为而造成损失；另一方面，通过动态分配机制，使用软件的组织也不再需要为每个用户都购买软件许可证，从而降低了软件购买费用。

购买浮动授权的计算机软件时，需要估算出合适的授权数量。购买的授权数量太多，会导致授权闲置，造成资源浪费；反之，购买的授权数量太少，会导致授权紧张，降低工作效率。估算授权数量的难点在于缺少明确的量化指标及其计算方法。

目前，软件采购实践中常用的估算方法有3种：1) 经验比例法。由预期的用户数量按照经验比例折算出浮动授权的购买数量。经验比例一般由软件供应商提供，是对众多用户使用情况的统计结果。但每个企业都有各自的特点，授权需求数量与用户数量的比例也会有所差异，直接套用这个经验比例，会产生较大的风险。2) 分批购买法。为了防止一次性购买的授权数量超过实际使用需求，可以分多批购买。先购买少量的授权，然后对使用情况进行监视，经过一段时间的统计，若发现授权数量不足，则再购买一批。多次重复此过程，直到授权数量满足要求。该方法可以有效降低购买风险，但是由于需要发生多轮软件购买、使用情况统计，效率较低。3) 试用统计法。购买之前，先从软件供应商处获取大量的试用授权，进行一段时间的试用，统计出授权的需求数量，再做出购买决策。该方法只需要一轮试用便可以准确统计出的授权的需求数量，效率较高。但是，如此规模的试用授权一般难以获取。在理论研究方面，文献[3]研究了浮动授权系统的数学模型，给出了一种授权数量的计算方法，但没有建立合适的量化指标，不能解决软件采购方的需求差异问题。文献[4]研究了某图书馆管理软件的浮动授权数量优化方法，但建立的数学模型不适应于一般的浮动授权系统。

本文首先基于排队理论建立了浮动授权系统的数学模型，提出以申请获准率作为确定浮动授权数量的量化指标，并以此为基础给出了一种软件浮动授权采购数量的估算方法。通过在某安全性分析软件采购活动中的应用对该数学模型进行了验证，并对该数学模型进行了适当的简化。

1 浮动授权系统的工作原理

浮动授权系统的工作原理如图1所示。软件客户端安装于诸多用户计算机上，软件授权安装于授权管理服务器上。当一个用户希望使用该软件时，通过网络向授权管理服务器发出授权申请。授权管理服务器检查授权总量和已占用授权数量，若有空闲授权，则准许该用户使用软件；否则，拒绝该用户使用软件。用户在完成软件使用后会通知服务器释放授权。授权管理服务器在准许用户使用或用户释放授权时会更新已占用授权数量。

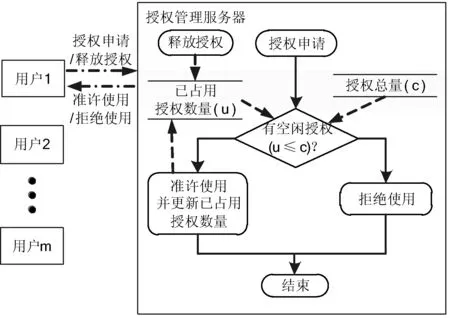
图1 浮动授权系统的工作原理图

浮动授权系统的关键规则包括：1) 当有空闲授权时，先申请的用户被许可使用软件；2) 同时使用软件的用户数量不得大于浮动授权的总量。

2 浮动授权系统的建模

2.1 排队论概述

排队是日常生活中经常遇到的现象。如顾客到商店购买物品，若待付款顾客的数量超过服务台数量，顾客就不能立即得到服务，因而就出现了排队现象。对于排队系统，如果服务设备太大，就会发生空闲浪费；如果服务设备太少，排队现象就会严重，对顾客体验造成不利影响。因此，排队系统的管理人员必须考虑如何取得平衡，以提高服务质量。排队论就是为解决上述问题而发展的一门学科。

排队论将排队系统分为输入过程、排队规则、服务机构三个部分。输入过程即指顾客到达排队系统的过程，其特征包括顾客的总体数量、到来的方式、相继到达的时间间隔等。排队规则，指系统从已到达顾客中选择服务对象的规则，可能包括先到先服务、随机服务、有优先权的服务等。服务机构的特征包括服务台数量、服务台的排列方式、服务方式、服务时间等。

排队论给出了排队系统的分类方法，并针对不同类型的排队系统建立了数学模型。应用排队论时，需首先分析待研究系统的特征，从而得到该系统的具体类型，然后建立数学模型并计算出该系统的评价指标，最后根据评价指标做出优化决策。

排队论使用Kendall符号X/Y/Z/A/B/C对排队系统进行分类。其中：

X表示顾客到达间隔时间的分布，可以为负指数分布(M)、一般服务时间分布(G)、k阶爱尔朗分布(Ek)、确定型分布(D)等；

Y表示服务时间的分布，也可以为负指数分布(M)、一般服务时间分布(G)、k阶爱尔朗分布(Ek)、确定型分布(D)等；

Z表示服务台个数；

A表示系统容量限制；

B表示顾客源数量；

C表示服务规则，可以为先到先服务(FCFS)、随机服务等。

2.2 浮动授权系统的排队类型

从浮动授权系统的工作过程描述可以发现顾客、排队规则、服务机构等排队系统的典型特征。因此，该系统可抽象为一种排队系统。为了确定浮动授权系统的具体类型，对排队系统的特征因素分析如下：

1) 顾客到达的间隔时间分布 基于如下假设和分析，可以认为授权申请的间隔时间符合参数为λ的负指数分布：

(1) 无后效性。在不相重叠的时间区间内用户发起授权申请的数量可以合理假设为相互独立。

(2) 平稳性和有限性。对充分小的时间Δt,在时间区间[t,t+Δt]内有1个用户发起授权申请的概率与t无关，而约与Δt成正比，即P1(t,t+Δt)=λΔt。实际情况与此假设可能会有偏差。例如，每个工作日刚开始上班时授权申请相对集中，而接近下班时授权申请则相对偏少。对此，我们仅建立授权申请较稳定的时段的数学模型。

(3) 普通性。对充分小的时间Δt, 在时间区间[t,t+Δt]内有2个或2个以上用户发起申请的概率极小，以致可以忽略不计。

2) 服务时间的分布 授权申请间隔时间的分析同样适用于授权占用时间。通过向软件供应商咨询或开展软件试用，可以得到授权占用平均时间(1/μ)。那么，授权占用时间符合参数为μ的负指数分布。

3) 服务台个数 浮动授权总量(c)即为服务台个数，一般为多个。

4) 系统容量限制 用户申请被拒绝后，即回到顾客源。该系统不存在有形的队列。文献[3]认为被拒绝用户，会像其他未申请过授权的用户一样在一段时间后再发起申请，因此认为系统的容量即为浮动授权总量，从而建立了M/M/c/c/m类型的队列模型。实际上，用户被拒绝后，其使用目的尚未达成，在等待一段时间后，必然再次发起申请。可以理解为被拒绝用户会进入一个虚拟队列等待授权准许。而且，授权管理服务器一般可以提供目前的授权占用状态，被拒绝用户可以据此在授权空闲时再次发起申请。因此，可以认为存在一个无限长的虚拟队列，即系统的容量为无穷大。

5) 顾客源数目 软件授权一般仅在特定范围内使用。因此用户总量(m)是有限的。

6) 服务规则 在有空闲授权时，先发起申请的用户获得授权。因此，该系统服务规则为先到先服务FCFS。

综上所述，软件浮动授权系统可以抽象为M/M/c/∞/m/FCFS类型的排队系统，如图2所示。其授权申请的间隔时间符合参数为λ的负指数分布，授权占用时间符合参数为μ的负指数分布，有c个服务台，系统容量为无穷大，顾客群为m。

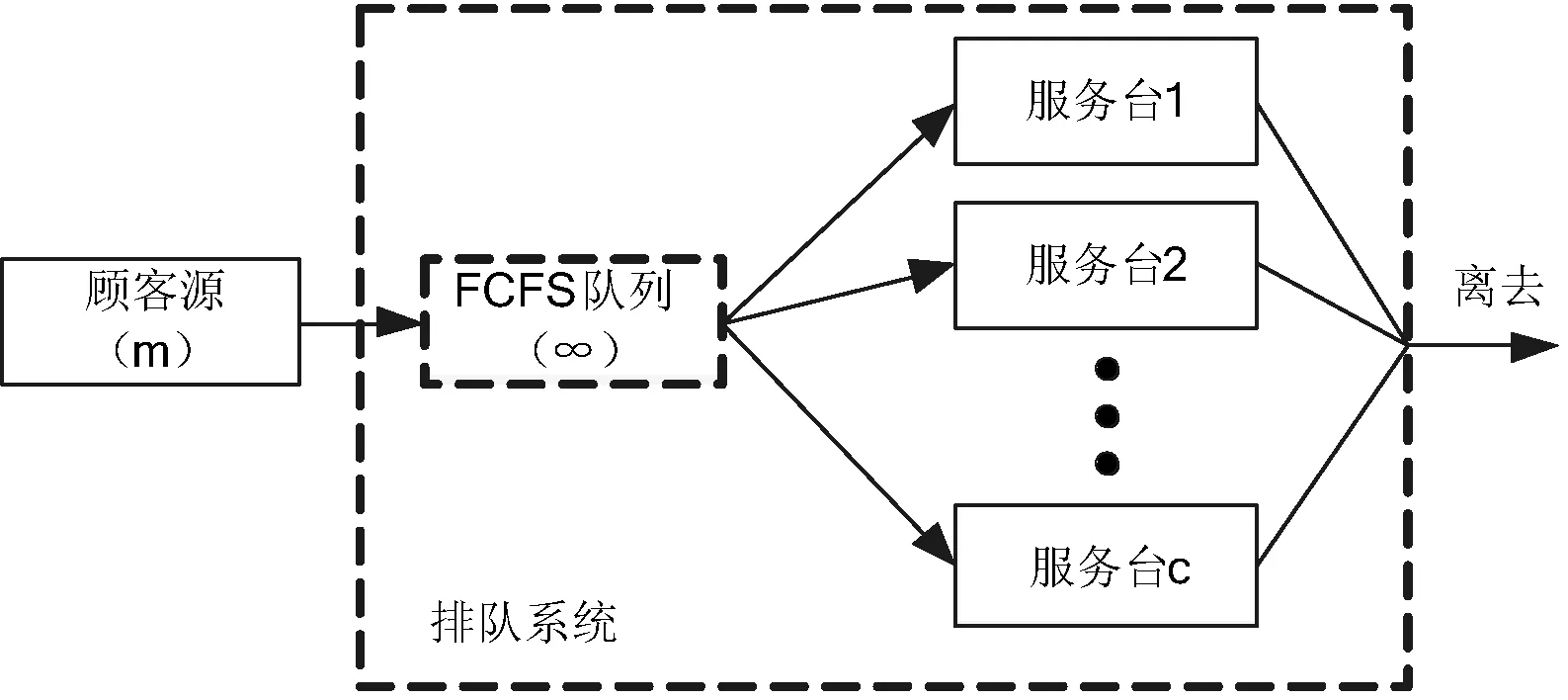
图2 M/M/c/∞/m/FCFS类型的排队系统结构图

2.3 浮动授权系统的数学模型

对于该排队系统，由排队理论可知，排队系统中有0个用户的概率为：

式中：

排队系统中有n个用户的概率为：

2.4 浮动授权数量估算方法

为了量化授权总量的适中程度，本文提出了申请获准率指标。该指标指某一时刻一个用户发出申请能够得到授权的概率。申请获准率越高，用户体验越好，工作效率越高，授权的使用频率越低。根据定义，购买c个授权时的申请获准率为：

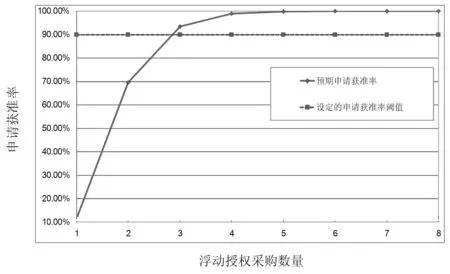
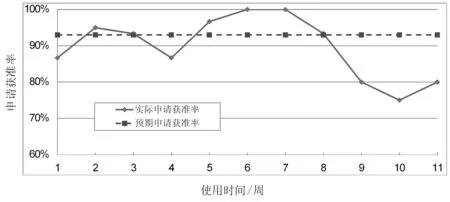
软件采购组织根据待采购软件的资金预算、关键程度、预期的用户体验度等情况设定一个申请获准率的阈值Gr。那么，软件采购的数量为：N=c,当G(c)≥Gr且G(c-1)

3 应用与验证

上述估算方法在某安全性分析软件采购时得到了应用。首先，从软件供应商处获取了少量的试用授权，并开展试用。试用期间对该软件的使用情况进行了统计。用户申请使用该软件的间隔时间(1/λ)平均为5 h。单个用户每次占用授权的时间(1/μ)平均为1 h。一段时期内使用该软件的用户数量(m)约为10人。软件采购组织根据自身需要设定的申请获准率阈值为90%。按照本文提出的估算方法，软件授权采购数量与预期的申请获准率的关系如图3所示。从图3可见，当购买的授权数量为3个时，获准率为93%。因此，该软件的浮动授权购买数量确定为3个。

图3 某软件的预期申请获准率与购买数量关系图

在该软件采购完成后，软件授权在一段时间内的实际使用情况如图4所示。实际获准率平均为90%，与预期基本相符。

图4 某软件的实际申请获准率情况

4 模型的简化与比较

在上述估算方法的应用过程发现本文提出的数学模型过于复杂，不便使用。在排队模型的基础上做如下假设：用户发起的授权申请都能得到准许。在授权的数量足够使用的情况下，这个假设近似成立。那么，单个用户在某时刻发起授权申请的概率为λ/μ。某个时刻，有n个用户发起授权申请的概率可简化为：

使用上述简化模型估算的某需求管理软件的浮动授权采购数量与使用排队模型估算的浮动授权采购数量的比较如图5所示。当申请获准率大于90%以上时，两者重合。以90%的授权获准率阈值计算，得到的购买数量为3个，与排队模型相同。因此，当软件采购组织设置的阈值大于90%时，可以采用简化模型进行授权购买数量估算。

图5 使用简化模型和排队模型估算的授权采购数量比较

5 结 语

本文基于排队理论建立了软件浮动授权系统的数学模型，提出以申请获准率为评价浮动授权数量适中程度的量化指标，并以此为基础给出了一种软件浮动授权采购数量的估算方法。通过在某软件采购活动中的应用对该估算方法进行了验证，并对数学模型进行了适当的简化。

在浮动授权数量估算过程中值得注意的是，组织对软件的使用需求可能是不稳定的，会随着组织的任务负荷、软件的推广程度等因素发生变化。以图4某软件的实际申请获准率情况为例，第8周以后随着软件的推广，申请获准率有所下降。因此，建议在软件采购前进行试用以统计出尽量准确的参数，并将本文的估算方法与分批购买法结合使用。

参 考 文 献

[1] 王琴琴,郭师虹.软件授权技术的研究[J].计算机技术与发展,2012,22(9):235-238.

[2] 陈智聪.基于浮动授权管理的许可证使用报表系统的研究与实现[D].广州:华南理工大学,2011.

[3] Murtojarvi M,Jarvinen J,Johnsson M,et al.Determining the Proper Number and Price of Software Licenses[J].IEEE Transactions on Software Engineering,2007,33(5):305-315.

[4] Quandt R E.On the optimum number of library software licenses[J].Journal of Economic Behavior & Organization,1999,38(3):349-356.

[5] 运筹学教材编写组.运筹学[M].北京:清华大学出版社,1990:310-348.

[6] 熊拥军,胡四元.排队理论在电子文献服务系统中的应用[J].现代图书情报技术,2008,24(11):82-85.

[7] He C X,Fu X D,Liu L,et al.Setting optional number of Web services in Web service communities based on queue theory[C]//IEEE International Conference on Software Engineering and Service Science.IEEE,2015:417-422.

[8] 杨晓妍.排队论在交通控制系统中的应用研究[D].青岛:青岛科技大学,2015.

[9] 林琳,高亚静.基于排队理论的充电站最优配置[J].电力科学与工程,2014,30(4):33-37.