自适应蝙蝠算法优化PF的风力机桨距系统故障诊断方法

曹 洁 杜永红 王进花

1(兰州理工大学电气工程和信息工程学院 甘肃 兰州 730050)2(甘肃省制造业信息化工程研究中心 甘肃 兰州 730050)

0 引 言

随着大功率风电机组安装规模与复杂程度增加，加之工作环境恶劣，导致各部件故障频发。因此，研究风电机组的故障诊断问题，对降低机组故障率，确保其安全稳定的运行具有重要的学术研究和工程实用价值[1]。变桨距系统作为风力机控制系统中的主要部件，对确保机组工作的安全性和输出功率的稳定性具有重要作用。

变桨距系统转速极低，运行不连续，负载随机，且受到复杂运行环境特殊性的约束，往往存在故障诊断难的问题[2]。目前，针对变桨距系统故障诊断问题的研究较少，主要是基于数据驱动和解析模型的故障诊断方法。前者需较多的变桨距系统的故障数据及先验知识，对所选数据的健康性和有效性要求较高，且此类方法构建的数据模型与变桨距系统的运行机理关系并不密切，故障诊断准确性不高。而基于解析模型的故障诊断方法主要是是基于系统的物理方程来构建模型，无需先验知识，对故障数据的依赖性更小，相比于其他方法估计性能更高。因此，在实际复杂设备的故障诊断中得到广泛应用。文献[3]主要利用模糊建模的方法，构造了基于模型的故障诊断结构，实现了桨距执行器及传感器的故障诊断问题的研究。文献[4]引入变遗忘因子的辨识算法，通过参数估计的思想，对变桨距系统的性能参数进行估计，从而进行故障诊断。文献[5]通过建立风机动态模型，采用其数学模型的方法对桨距系统进行故障检测。文献[6]详细介绍了多信息观测器的设计方法，并实现桨距系统故障检测。以上方法基于不同出发点，针对变桨距系统的故障诊断问题取得了相对较好的效果。但风电机组是多参数、强耦合的非线性系统，实际情况下，系统存在各类信号扰动和随机噪声的影响，以上文献并未对此类问题进行深入研究，导致故障诊断的准确性不高。有学者提出采用扩展卡尔曼滤波(EKF)方法用于变桨距系统故障诊断[7],但该方法涉及雅可比矩阵的计算，忽略高阶项，在处理变桨距系统这类复杂非线性系统时会引入额外误差且计算量较大。而粒子滤波(PF)不受限于系统非线性及噪声分布特性，更加适用于处理变桨距系统这种处于复杂噪声影响下的非线性较强的系统[8-9]。

粒子滤波算法存在粒子贫化现象,导致故障诊断的准确性不高[10]。本文考虑到蝙蝠算法寻优特性的优势，将其与粒子滤波融合，并结合最新观测值优化粒子的采样过程。同时引入动态自适应惯性权重优化粒子的全局搜索方式，自适应控制粒子的全局搜索与局部搜索的相互转换，缓解粒子的贫化现象。在此基础上，以4.8 MW级双馈变速恒频风电机组为研究对象，对风电机组变桨距系统的故障诊断问题进行仿真分析。

1 风电机组模型

变速恒频双馈风电机组主要由空气动力学系统、传动系统、变桨距系统、功率转换系统和控制器等部件[11]组成。其主要结构关系如图1所示。

图1 风力机系统模型结构

其中，vw为有效风速，β为桨距角，βref为桨距角参考值，Ta为气动转矩，ωr为转子速度，Tg为发电机的转矩，ωg为发电机转速，ωr,m为实测转子转速，Tg,m为实测发电机转矩，ωg,m为实测发电机转速，Pg为发电机产生的电能，Pr为功率参考值，Tg,r为发电机转矩参考值。

风电机组工作在额定风速以下时，改变定子电压控制发电机转矩，从而调节发电机转速，并通过调节桨距角使机组保持最优功率跟踪。机组运行于额定风速以上时，变桨距系统通过调节桨距角限制风轮捕获的机械能，实现机组恒功率输出。变桨距系统工作在变速变载荷条件下，是风力机状态监测的关键部件。

本文研究的是三叶片水平型风力机，其有三个完全一致且独立的变桨距系统，文中仅研究其中一个变桨距系统。桨距系统执行器或桨距角传感器发生故障，导致变桨距系统动态响应变慢，桨距角不能迅速跟踪参考桨距角变化，引发机组输出功率发生波动。为研究变桨距系统故障诊断问题，本文根据风力机基本工作原理，对4.8 MW风电机组建模如下式所示：

(1)

式中：Jg为高速轴的转动惯量、Jr为低速轴的转动惯量；θΔ为传动系统的扭转角；Kdt和Bdt分别为弹性装置的刚性系数和阻尼系数；Bg为发电机固有阻尼；Ng为传动比；ζ和ωn分别为变桨距系统的阻尼系数和固有频率。

2 粒子滤波算法

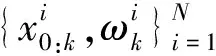
(2)

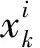
3 基于改进蝙蝠算法的粒子滤波方法

标准粒子滤波中采用次优密度函数作为重要性密度函数进行采样，未考虑当前时刻观测值，会产生粒子权值退化现象。重采样方法通过舍弃小权值粒子来克服粒子权值退化问题，但经过多次迭代后，将导致粒子的贫化问题。针对以上问题，本文利用改进后的蝙蝠算法改善粒子滤波的采样过程，通过全局最优值引导粒子的移动，使得粒子集在权值更新前已趋向于高似然区域，但不会全部聚集在最优值附近，通过改善粒子的分布来提高算法的估计精度。

3.1 蝙蝠优化算法的原理

蝙蝠算法[13]BA(Bat Algorithm)是一种最新的仿生学群体智能的优化算法，其通过模拟自然界中蝙蝠利用回声定位进行搜索捕食猎物的行为而进行自适应迭代寻忧，具有模型简单、收敛速度快、鲁棒性好等优点。蝙蝠算法的寻优能力优于粒子群优化算法等其他主流群体智能优化算法[14]。该算法主要思想是蝙蝠依据所发出的脉冲频率、音强、脉冲发射频度的不断更新来实现目标优化，其中脉冲频率决定了蝙蝠飞行速度的大小，音强和脉冲发射频度决定了蝙蝠个体在更新后，接受新位置的概率。具体优化机理如下：

(1) 在D维搜索空间中，蝙蝠个体i在k时刻的速度vi和位置xi的更新方式定义为：

fi=fmin+(fmax-fmin)·β

(3)

(4)

(5)

(2) 局部搜索时，每只蝙蝠的新位置xnew由当前最优位置随机扰动产生，位置更新方式如公式所示：

(6)

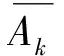
(3) 蝙蝠在搜索猎物的初始阶段，具有较大的脉冲音强Ai和较低的脉冲发射频度ri，以利于大范围搜索，一旦搜索到猎物，就逐渐减小脉冲音强，并且增大脉冲发射频度，从而更容易捕捉到猎物所在的位置。Ai和ri的更新方式如下所示：

(7)

(8)

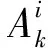
3.2 全局搜索位置更新方式的自适应更新

标准蝙蝠算法通过搜索脉冲频率f控制蝙蝠移动的范围和空间，从而控制算法的全局与局部搜索能力。但随着迭代次数增加，利用式(3)-式(5)更新蝙蝠的位置和信息时，蝙蝠的速度会越来越小，蝙蝠群体聚集到局部极值附近，算法缺乏有效的变异机制，导致种群多样性降低，从而影响收敛精度。针对该问题，本文受文献[15-16]改进思想的启发，本文对蝙蝠位置更新方式进行优化，设计一种新的全局搜索公式，通过引入一种动态自适应惯性权重控制蝙蝠飞行位置变化幅度。新的位置更新方式如下：

(9)

ω(k-1)=exp(-λ(k-1)/λ(k-2))

(10)

(11)

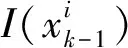
3.3 改进的蝙蝠算法优化粒子滤波

将粒子随机分布在搜索空间中，通过粒子来表征蝙蝠个体，模拟蝙蝠群体搜索猎物的过程。在初始迭代时刻，粒子采用较低的脉冲发射频度和较大的音强进行全局搜索，从而更新粒子状态；随后进行局部搜索，同时逐渐减小音强，增大发射频度。粒子群体通过调整频率，响度及脉冲发射频度追随当前最优粒子进行搜索，以改善粒子多样性匮乏问题。为考虑滤波精度，本文在蝙蝠算法优化采样粒子的过程中引入最新观测值，定义适应度函数为：

(12)

式中：ynew是最新观测值，ypred是滤波器预测的观测值，Rk为观测噪声方差。从适应度函数值的计算公式可看出，其充分发挥了每个时刻最新观测值对算法内部信息交互的指导作用。通过和较优位置的粒子比较，多次迭代后，粒子逐渐趋向于搜索空间中的最优位置周围，同时，设置迭代终止阈值ε，若满足该条件，终止迭代，从而确保算法在速度和精度方面的优势。

3.4 算法实现步骤

本文改进算法的实现步骤如下：

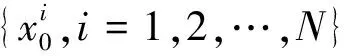
步骤3改进蝙蝠算法优化采样粒子。

1) 模拟的蝙蝠的全局搜索行为。依据式(3)、式(4)和式(9)-式(11)更新粒子的频率、速度和位置。

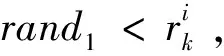
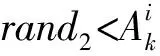
4) 计算并对比粒子适应度函数值，更新全局最优值。

(13)

步骤4当算法达到设定的阈值ε或最大迭代次数时，停止迭代优化，否则转入步骤2。

步骤5计算优化后粒子的重要性权值并归一化。

(14)

步骤6状态输出。

(15)

4 仿真结果与分析

4.1 算法性能测试

为验证IBA-PF算法的性能，本文利用典型一维非线性系统模型[8]进行仿真验证，并与PF、UPF和PSO-PF进行对比。实验环境为Intel Core i3-4170@3.70 GHz,内存为4 GB，操作系统为Windows7。

一维非线性系统模型如下：

(16)

式中：模型的系统噪声uk-1～Γ(3,2)，观测噪声vk～N(0,0.000 1)，实验中，总的观测时间为T=50，假设状态初值为2，粒子数目分别设置为N=100和N=50，最大脉冲发射频度r0=0.5，最大脉冲音强A0=0.25，fmin=0，fmax=2，最大迭代次数为10，脉冲频度增强因子γ=0.05，脉冲音强衰减因子α=0.95，优化终止阈值ε=0.01。为对比四种算法的跟踪性能，采用均方根误差、平均有效粒子数和一次运行平均时间作为评价算法优越性的指标。均方根误差定义如下：

(17)

式中：M为蒙特卡洛仿真次数，实验中设置为100。

(18)

图2 不同滤波算法的状态估计结果

图3 不同滤波算法的RMSE对比结果

参数算法RMSEN-eff时间/svk～N(0，0．001)PF1．060412．10560．2339UPF0．510514．40980．5133PSO⁃PF0．302816．61391．0177IBA⁃PF0．090625．26190．9253vk～N(0，0．01)PF0．824214．27090．5930UPF0．414016．11050．8356PSO⁃PF0．233617．02112．0163IBA⁃PF0．063332．40651．8638

4.2 变桨距系统故障诊断仿真与分析

变桨距系统存在的故障主要有桨距系统执行器故障和桨距角传感器故障，其中执行器故障主要有油液空气含量高、液压泄露、泵磨损、阀阻塞等故障。文中主要选取油液空气含量高、液压泄露及桨距角传感器偏差故障，利用本文所改进的故障诊断方法进行变桨距系统故障诊断仿真。针对第1节中所建立的风电机组动力学模型，构建系统的状态空间模型如下所示：

(19)

故障1：油液空气含量高故障。变桨距系统执行器的固有频率由正常值11.11 rad/s跳变为5.73 rad/s，阻尼系数由0.6跳变为0.45。

故障2：油液空气含量高故障。变桨距系统执行器固有频率和阻尼系数分别由正常值变为3.42 rad/s和0.9。

故障3：桨距角传感器偏差故障。桨距角传感器失效，发生偏差为0.3的故障，导致对桨距角的测量值不准确。

实验中，假设机组运行于额定风速以上，系统的初始状态x=[0.404 63 162 5.6 0.504]T，输入u=[5.9154×107500 4.5]T，采样粒子数N=200，仿真时间T=200 s，离散步长ΔT=0.01 s。考虑系统中存在未知噪声等干扰的影响，选择滑动窗口宽度M=20。假设在0 s≤t<100 s时，系统处于正常状态，100 s≤t≤200 s时，系统处于故障状态。

4.2.1 故障检测结果及分析

利用本文改进粒子滤波的状态估计方法，结合残差平滑法进行故障检测。故障检测结果如图4所示。

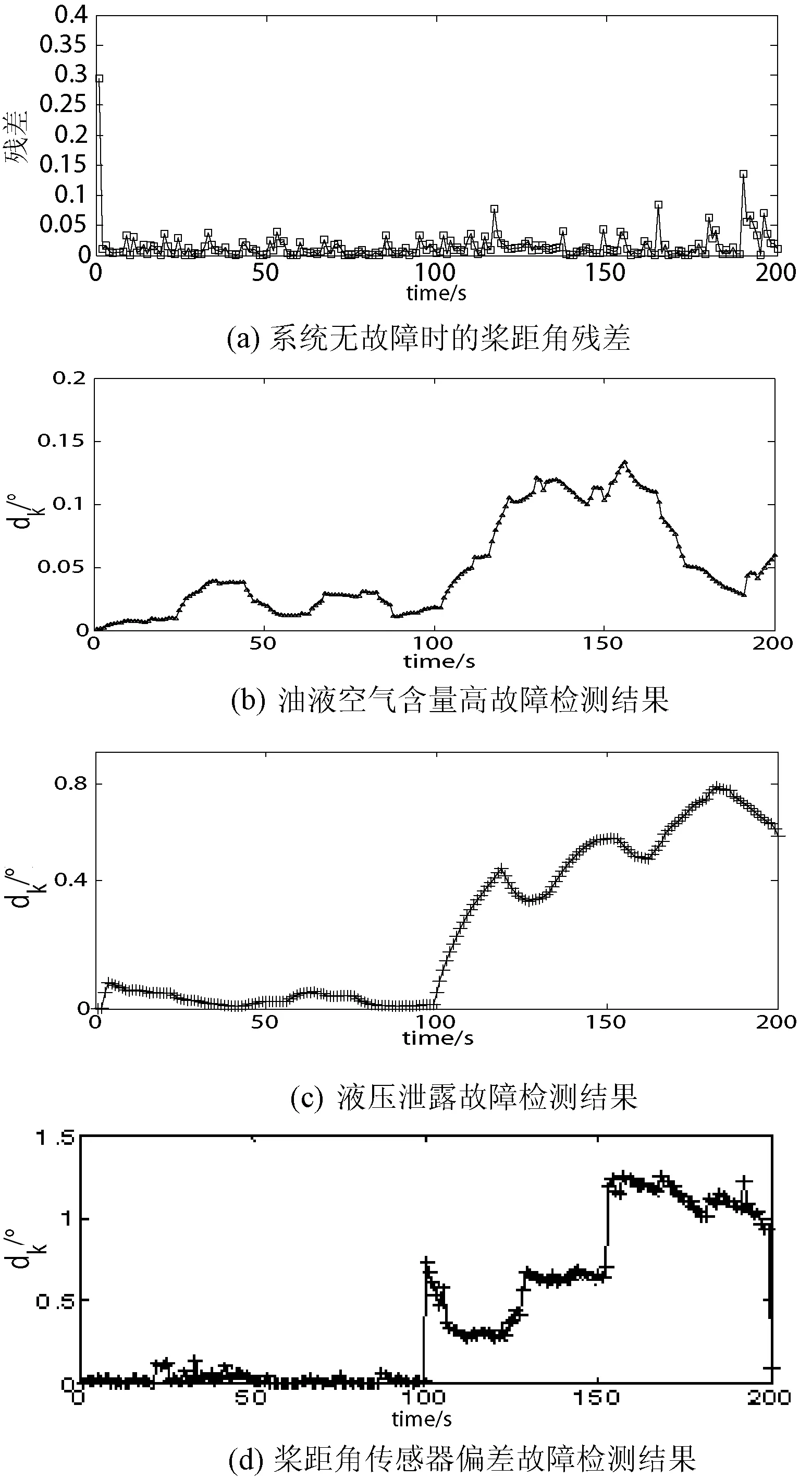
图4 三种故障的故障检测结果

由图4(a)可以看出，系统无故障时，桨距角残差值基本为0，表明本文方法能够很好地跟踪桨距角的变化，估计误差较小。由图4(b)、图4(c)、图4(d)可以看出，对于油液空气含量高、液压泄露故障和桨距角传感器偏差故障，在0s≤t<100s时，即系统无故障时，系统桨距角残差平滑值较小,且变化比较平稳，100 s≤t≤200 s时，即在故障发生后，桨距角残差平滑值dk都有剧烈跳变。依据残差平滑值的变化可进行故障检测。以上表明本文算法可以有效地实现故障检测。

4.2.2 桨距系统故障隔离结果

由图5(a)可知，传感器偏差故障和液压泄露故障模时的桨距角残差平滑值均较大，而油液空气含量高故障模式的桨距角残差平滑值是最小的，故判断发生油液空气含量高故障；图5(b)和图5(c)的隔离过程类似，不再赘述。对于变桨距系统的上述三种故障，本文方法都能够快速有效地对其进行隔离定位。

5 结 语

本文针对传统粒子滤波方法在处理风电机组变桨距系统故障诊断问题时因存在粒子贫化现象，导致故障诊断准确性不高的问题，提出了一种基于蝙蝠算法优化的粒子滤波状态估计方法。通过将蝙蝠算法融入到粒子滤波的采样过程，利用蝙蝠算法的全局搜索与局部搜索机制引导粒子向真实状态移动，同时利用系统最新量测值来定义适应度函数，有效缓解样本枯竭问题。引入动态自适应惯性权重改进粒子的全局搜索位置更新方式以控制粒子的多样性与收敛速度的平衡。仿真结果表明应用本文方法能够有效地提高变桨距系统故障检测和故障隔离的准确性，为实际工程应用提供了借鉴思路。

参 考 文 献

[1] Perveen R,Kishor N,Mohanty S R.Off-shore wind farm development:Present status and challenges[J].Renewable and Sustainable Energy Reviews,2014,29(7):780-792.

[2] Odgaard P F,Johnson K E.Wind turbine fault detection and fault tolerant control-An enhanced benchmark challenge[C]//American Control Conference (ACC),17-19 June 2013,Washington,DC,USA.IEEE,2013.

[3] Simani S,Farsoni S,Castaldi P.Fault Diagnosis of a Wind Turbine Benchmark via Identified Fuzzy Models[J].IEEE Transactions on Industrial Electronics,2015,62(6):3775-3782.

[4] Wu D,Song J,Shen Y.Variable forgetting factor identification algorithm for fault diagnosis of wind turbines[C]//Chinese Control and Decision Conference.2016:1895-1900.

[5] 赵洪山,连莎莎,邵玲.基于模型的风电机组变桨距系统故障检测[J].电网技术,2015(2):440-444.

[6] Wu D,Zhai Y,Gao W,et al.Multi-innovation observer based fault detection for pitch system of wind turbines[C]//IEEE International Conference on Cyber Technology in Automation,Control,and Intelligent Systems.IEEE,2015:677-680.

[7] Esbensen T,Sloth C.Fault diagnosis and fault-tolerant control of wind turbines[D].Aalborg University,2009.

[8] 张玲霞,刘志仓,王辉,等.非线性系统故障诊的粒子滤波方法[J].电子学报,2015,43(3):615-619.

[9] 郭健彬,纪丁菲,王鑫,等.混杂系统粒子滤波混合状态估计及故障诊断算法[J].系统工程与电子技术,2015,37(8):1936-1942.

[10] 黄金泉,陈煜,周浩文,等.基于QPSO粒子滤波的航空发动机突变故障诊断[J].南京航空航天大学学报,2014,46(4):494-500.

[11] Liu X,Gao Z.Takagi-Sugeno fuzzy modelling and robust fault reconstruction for wind turbine systems[C]//IEEE,International Conference on Industrial Informatics.IEEE,2017:492-495.

[12] 朱志宇.粒子滤波算法及其应用[M].科学出版社,2010.

[13] 李煜,马良.新型全局优化蝙蝠算法[J].计算机科学,2013,40(9):225-229.

[14] Gandomi A H,Yang X S,Alavi A H,et al.Bat algorithm for constrained optimization tasks[J].Neural Computing & Applications,2013,22(6):1239-1255.

[15] 陈志敏,田梦楚,吴盘龙,等.基于蝙蝠算法的粒子滤波法研究[J].物理学报,2017,66(5):41-50.

[16] 朱奇光,肖亚昆,陈卫东,等.基于萤火虫算法改进移动机器人定位方法研究[J].仪器仪表学报,2016,37(2):323-329.