基于拥堵工况辨识的车辆自动变速器换挡控制∗

夏 光，邹 斌，唐希雯，陈无畏

(1.合肥工业大学汽车工程技术研究院，合肥 230009； 2.国防科技大学电子对抗学院，合肥 230037；3.合肥工业大学汽车与交通工程学院，合肥 230009)

前言

车辆在拥堵工况下，驾驶员为了跟车与行车安全，频繁踩踏加速踏板和制动踏板，车速与节气门容易突变，导致车辆频繁换挡，因此需要辨识拥堵工况，并制定合理的拥堵工况换挡控制策略。文献[1]中通过选取车辆在拥堵路况行车实车参数，识别车辆处于蠕行状态，车速较低，节气门开度较小，且常伴有制动操作，提出以单位时间内加减速次数为辨识参数，辨识拥堵工况，但准确性不高。文献[2]中基于模糊规则提出对城市工况巡航控制，但没有明确辨识交通拥堵工况。文献[3]中根据不同等级道路和不同类型浮动车的行驶特性，得出各类型车辆在不同等级道路的平均速度分布特性、样本分布特性和各等级道路每公里每小时的平均样本量，通过选取多参数搭建城际交通拥堵识别模型，但实施繁琐。文献[4]～文献[8]中通过选取特征值，采集大量样本交通流、占有率等参数，利用识别模糊C均值聚类，神经网络等方法识别道路拥堵，但对单个车辆动力系统而言意义不大。文献[9]中根据城市拥堵时节气门开度频繁变化这一特征制定拥堵行车换挡修正控制，并没有提出完整的识别拥堵方法。文献[10]中提出以车辆轨迹辨识拥堵工况，但该方法对传感器要求精度高且耗费大。

本文中通过构建T-S模糊神经网络并对该网络模型训练，进行拥堵工况辨识，在拥堵工况辨识的基础上采用拥堵工况换挡分层修正控制策略，并进行建模仿真与实车试验验证。

1 T-S模糊神经网络结构与算法

车辆处于拥堵工况时各参数相对于畅行工况明显不同，各参数之间又存在一定的关联，具有很强的模糊性，T-S模糊神经网络模型能综合考虑多种因素的影响及其相互关系。利用T-S模糊神经网络实现车辆拥堵工况辨识，不必对过程或对象内部进行分析，只要用测得的过程输入输出变量，据此对T-S模糊神经网络进行训练，就可获得其输入输出特性与实际过程相近的拥堵辨识T-S模糊神经网络。

1.1 T-S模糊系统

T-S模糊系统作为函数模糊系统的一种特例，由于构成的各条规则采用的都是线性方程作为结论，使得模型的全局输出具有良好的数学表达特性，在处理多变量系统时能有效减少模糊规则个数，具有很大的优越性[6]。该模型不仅能自动更新，而且能不断修正模糊子集的隶属度函数[7]，可用“ifthen”规则形式来定义[8]。

设输入向量x＝[x1x2…xn]T，每个分量xi均为模糊语言变量，本文中为车辆行驶参数，并设

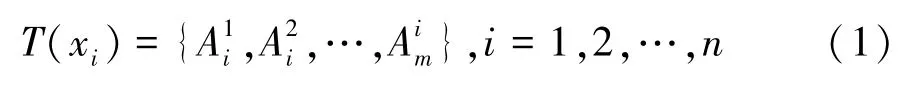
在规则Ri的情况下，其表达式为

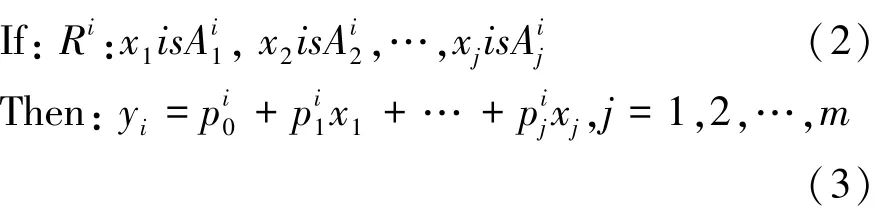
式中：xj为车辆拥堵辨识参数；为xi的第i个语言量值；Ri为第i条模糊规则为模糊系统参数；yi为根据模糊规则得到的输出，为车辆拥堵工况判别输出；If为车辆辨识模型模糊前提或者前件；Then为车辆拥堵判别模糊结论；m为每组车辆拥堵辨识参数的分量；n为xj的模糊分割数。

1.2 T-S模糊神经网络

为了通过实车参数对拥堵辨识T-S模糊神经网络进行训练，建立T-S模糊神经网络，如图1所示。T-S模糊神经网络模型共有5层，各层网络关系如下。

(1)输入层：该层有n个节点直接与输入节点x相连接，将所选取的车辆拥堵辨识参数输入值x＝[x1x2…xn]，传送到下一层，该层不对数据进行处理。

(2)语言模糊化层：该层的每一个节点代表一个语言变量值，如NM，PS等，对上一层输入的车辆拥堵辨识参数进行模糊等级划分。它的作用是计算各输入车辆拥堵辨识参数分量属于各语言变量值模糊集合的隶属度函数即

(3)规则层：每一个节点代表系统的每一条拥堵判别规则，根据式(4)计算出每条规则的隶属度。将各隶属度进行模糊计算，采用的模糊算子为连乘算子：

式中Wi为模糊规则适用度。对于给定的输入车辆参数，只有在输入点附近的语言变量值才有较大的隶属度值，远离输入点的语言变量值的隶属度值很小，或者为零。

(4)去模糊化层：该层的作用是对模糊系统各条规则的归一化计算。

(5)输出层：采用加权平均去模糊化，计算模糊系统的输出值yi：

式中pj为模糊系统参数。

基于标准型T-S模糊神经网络结构(图1)，拥堵辨识的T-S模糊神经网络m为输入量的维数3，n为模糊分割数3。

图1 T-S模糊神经网络结构图

1.3 T-S模糊神经网络学习算法

T-S模糊神经网络是根据网络输出和期望输出的误差来不断修正模糊系统系数和隶属度函数参数，从而使T-S模糊神经网络不断地逼近期望输出，其学习修正算法如下。

(1)误差计算

式中：yd为拥堵辨识网络的期望输出；yc为拥堵辨识网络的实际输出；e为期望输出和实际输出的误差。

T-S模糊神经网络的训练原理就是不断修正模型中的模糊系统参数隶属度函数中心值和宽度，使得误差e逐渐减小，即使得模型预测所得车辆拥堵等级逐渐逼近实际拥堵等级。当误差符合精度要求时，训练结束。

(2)模糊系统的系数修正

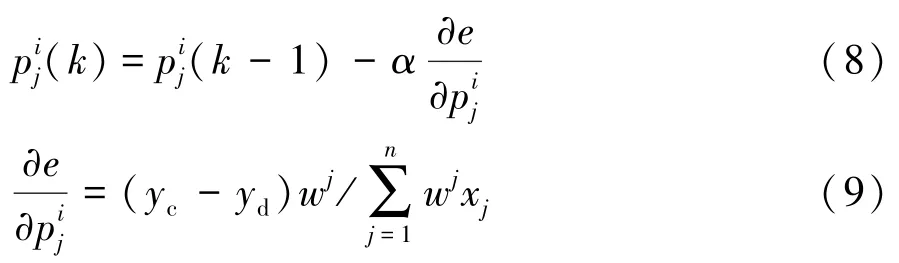
式中：k为迭代次数；α为网络学习率；xj为网络输入参数(即车辆拥堵辨识参数)；wj为隶属度连乘积。

(3)隶属度参数修正

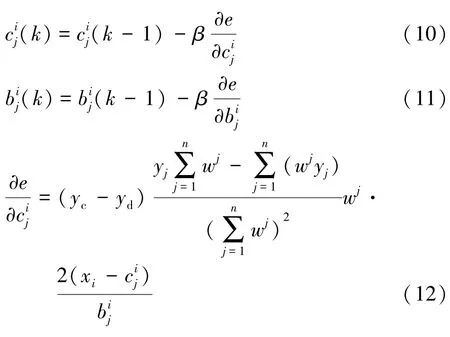
式中β为隶属度函数调整因子。

2 T-S模糊神经网络拥堵辨识模型

2.1 参数选取

车辆行驶特征可由平均速度、最高速度、速度的平方和、速度的标准差、平均加速度、正负加速度平均值等一系列参数描述。车辆在拥堵工况时，车速极低，节气门开度较小且伴随着制动操作，考虑到参数的独立性，根据北京市地方标准《城市交通管理评价指标体系》规定平均速度为交通拥堵工况评价指标。定义平均节气门开度为样本时间内平均每秒节气门开度，即

式中：为平均节气门开度；αi为采样时车辆节气门开度。

平均节气门开度不仅可以反映驾驶员加速意图，而且可以表征一段时间内车辆的行驶加速度特征；样本时间内制动踏板作动次数可以反映驾驶员减速意图。综上所述，选取样本时间内车辆平均车速、样本时间内车辆平均节气门开度和样本时间内制动踏板作动次数为T-S模糊神经网络输入量。

2.2 T-S模糊神经网络拥堵工况辨识

2.2.1 训练样本

为了保证样本的准确性以及多样性，通过实车采集合肥市一环路早晚高峰非常拥堵、一般拥堵、畅行状态车辆参数各40组，分别记样本A、样本B、样本C，每组参数包含3个分量(样本时间内车辆平均车速、样本时间内平均节气门开度、样本时间内制动踏板作动次数)。选取样本A，B，C，各取30组共90组数据构成训练样本，选取剩余数据中12组作为测试样本。为提高运算速度和误差精度，需要对训练样本数据和测试样本共102组数据进行归一化处理，运用极值标准化值公式，即

式中：i＝1，2，3，…，102为样本中任意一组车辆参数某个因子值；xj为数据分量和分别为中的最小值和最大值；xij为标准化后的指标。

2.2.2 T-S模糊神经网络训练与预测

根据训练样本的维数，确定T-S模糊神经网络结构参数。由于输入数据含有3个分量为3维，每个输入分量神经元语言变量为3，输出数据为1维，模糊神经网络的结构为3-9-1，即有9个隶属度函数。利用T-S模糊神经网络学习算法对训练误差不断调整，修正模糊系统参数p0～p3和模糊隶属度函数中心c和b。神经网络训练300次，训练误差如图2所示，不断趋于零。

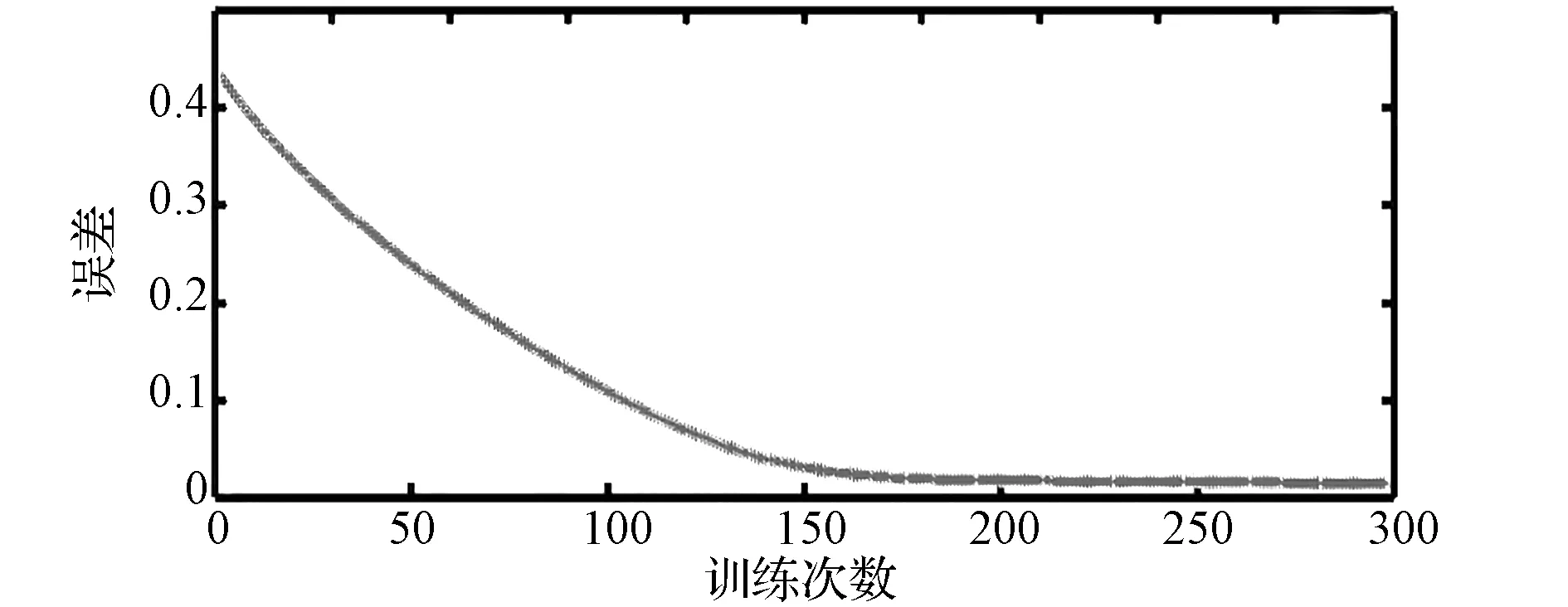
图2 网络训练误差图

由网络训练误差图得知T-S模糊神经网络模型在训练中不断进化。利用测试数据对训练好的网络进行测试，T-S模糊神经网络预测流程如图3所示。

图3 T-S模糊神经网络预测流程图

将车辆行驶工况分为一级(畅行)、二级(一般拥堵)和三级(非常拥堵)，依次取期望目标输出为1，2，3。用测试样本对T-S模糊神经网络进行测试，在网络输出值的基础上按照四舍五入原则确定车辆拥堵评级。

预测结果如图4所示，预测结果与车辆所处工况全部相符，说明T-S模糊神经网络有良好的预测能力，因此本文中建立的T-S模糊神经网络模型在拥堵评价方面有着优异的性能，适用于拥堵工况辨识。

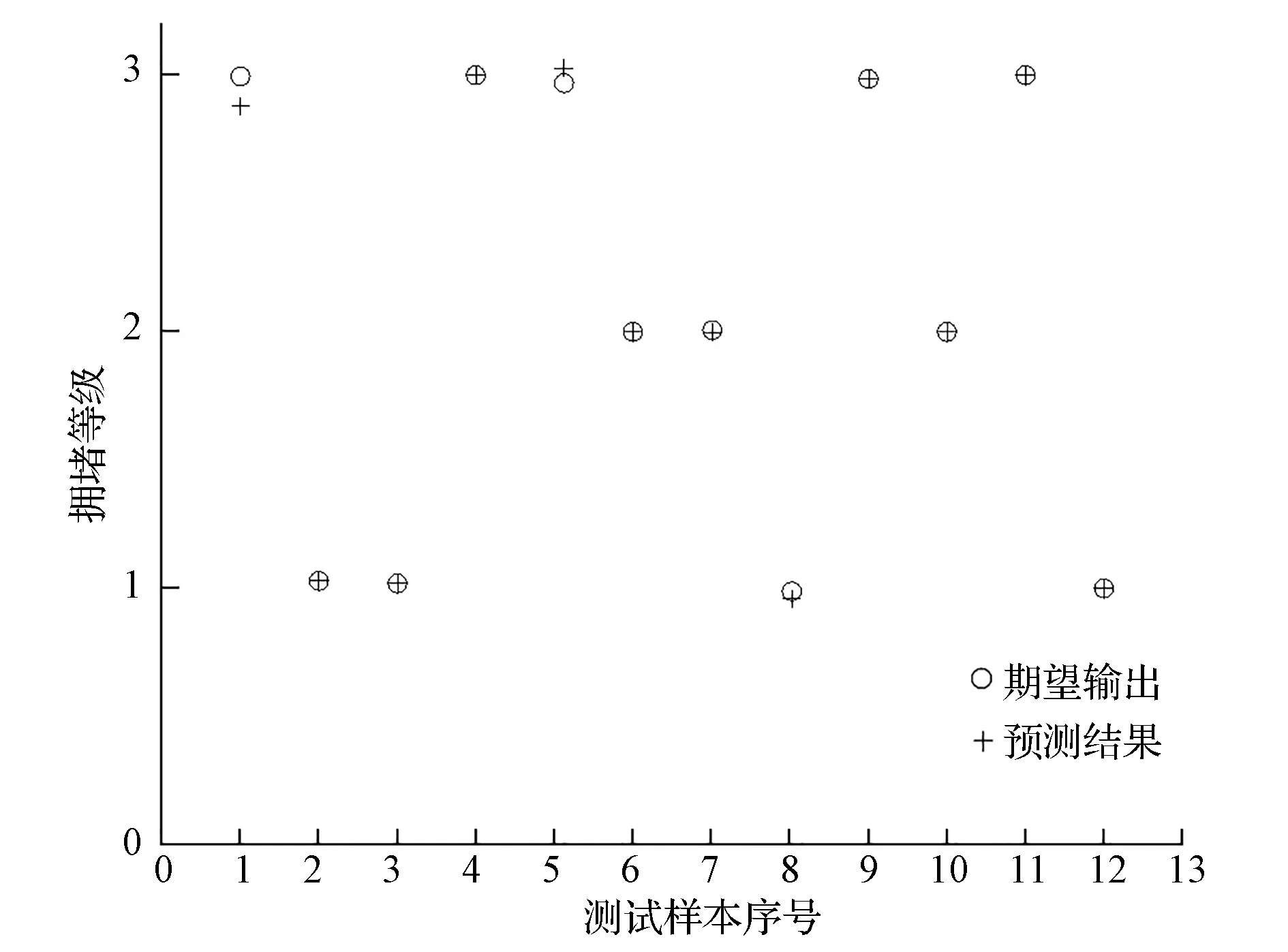
图4 样本预测结果图

2.2.3 拥堵工况辨识

为了提高车辆拥堵工况辨识的准确性，通过辨识车辆5个连续行驶时长为20s的工况片段的行驶状态，依据专家经验，得到车辆行驶拥堵工况。若车辆类似极其拥堵工况片段数n1≥3，则车辆行驶工况为非常拥堵工况；若车辆类似畅行工况片段数n2≥4，则车辆行驶工况为畅行工况；其余为一般拥堵工况。

3 换挡分层修正控制策略

车辆在拥堵工况行驶时，车辆自动变速采用换挡分层修正控制策略，将车辆自动变速分为上层辨识决策层与下层换挡执行层，换挡分层修正流程如图5所示。

上层决策层采集车辆行驶参数，基于T-S模糊神经网络进行拥堵工况辨识，将拥堵工况分为畅行、一般拥堵和非常拥堵3个等级。当车辆处于畅行工况时，车辆自动变速按照基本换挡规律换挡，不进行换挡修正和干预；当车辆处于一般拥堵和非常拥堵工况时，根据拥堵等级制定相应的换挡修正策略，并发送换挡修正控制指令至下层执行层。下层换挡执行层接收上层换挡修正指令，完成换挡修正。

图5 换挡分层修正流程图

4 整车动力学模型

4.1 发动机模型

由于车辆运行的环境复杂，发动机不可能一直维持在稳态转矩特性。大量研究表面，发动机的动态转矩特性与稳态转矩特性存在较大差异。因此，为了保证发动机模型准确性，利用修正系数修正发动机稳态特性，计算方法为

式中：Ted为发动机动态工况输出转矩；Te为发动机稳态工况输出转矩；λ为发动机非稳态工况下的输出转矩下降系数，λ的取值与发动机有关，取值范围为0.07～0.09；ωe为发动机输出曲轴的角速度。

发动机仿真模型如图6所示。

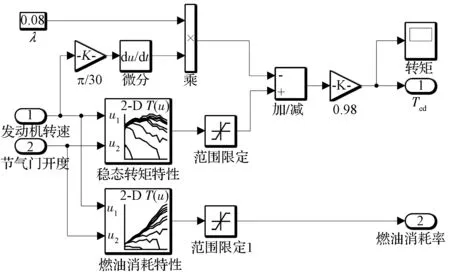
图6 发动机仿真模型

4.2 变速器模型

变速器的主要功能在整车动力系统中承担着承上启下的作用，接受并调节发动机产生的转矩传与转速，然后递给车辆驱动轮，从而使得车辆行驶。将变速器看做一个比例环节，即

式中：Tout为变速器输出转矩；ig为变速器传动比；ηT为传动系统效率。

变速器仿真模型如图7所示。

4.3 车辆动力学模型

图7 变速器仿真模型

由于车辆的行驶过程十分复杂，为了研究方便，对车辆的行驶过程做了以下假设和简化[15]：(1)车辆在良好的道路上作直线运动；(2)理想化车辆为单一自由度，只能纵向行驶；(3)理想化车辆为轴对称且受力均匀。

车辆直线行驶时的总阻力为

式中：Ff为滚动阻力；Fw为空气阻力；Fi为坡度阻力；Fj为加速阻力。

空气阻力可以表示为

式中：CD为空气阻力系数；A为车辆迎风面积；va为车速。

滚动阻力和坡道阻力可以表示为

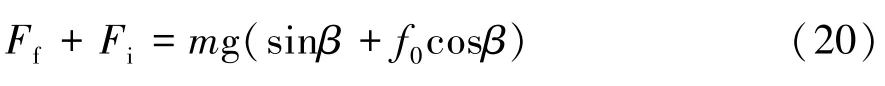
式中：β为坡度角；f0为车辆的滚动阻力系数。

加速度阻力可以表示为

式中：σ为质量换算系数；a为车辆行驶加速度。

车辆行驶动力方程为

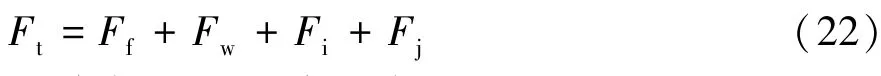
驱动力Ft可以表示为

式中：a为节气门开度；ne为发动机转速；i0为主减速器传动比；R为有效滚动半径。

依据车辆行驶的平衡方程(式(22))，建立车辆纵向动力学模型，如图8所示。

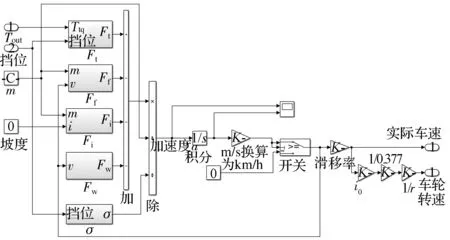
图8 车辆动力学模型

4.4 整车动力学模型

在Matlab/Simulink平台针对目标车型建立整车动力学模型，由发动机仿真模型、变速器仿真模型、车辆动力学仿真模型等共同组成。整车动力学模型如图9所示，整车参数如表1所示。

图9 整车动力学模型图

表1 整车参数

5 仿真与结果分析

利用前文基于Simulink搭建整车模型，分别采用拥堵辨识的“换挡分层修正控制策略”与未采用换挡修正控制的“独立换挡控制策略”进行仿真，仿真工况为在非常拥堵工况与一般拥堵工况。

(1)非常拥堵工况

车辆处于非常拥堵工况，采用独立控制策略的挡位如图10所示。

图10 独立控制挡位图

由图可见：车辆以1挡行驶，此时车辆节气门开度小，车速低；当前方车辆加速时，驾驶员为了跟车，增大节气门开度，当达到基本换挡规律的升挡点时，车辆挡位升为2挡；当前方车辆减速时，驾驶员为了行车安全，利用制动踏板减速，此时车速减小，当达到基本换挡规律的降挡点时，车辆挡位由2挡降为1挡，这种频繁的升降挡一直持续到拥堵结束。

采用拥堵辨识换挡分层修正控制策略的挡位如图11所示。

由图可见：车辆以1挡行驶，此时车辆节气门开度低，车速低；当前方车辆加速时，驾驶员为了跟车，增大节气门开度，当达到基本换挡规律的升挡点时，车辆挡位应升至2挡，但是T-S模糊神经网络识别的拥堵工况为非常拥堵，根据非常拥堵工况的换挡修正策略，需要限制车辆升为2挡，保持1挡行驶，避免频繁换挡，降低了换挡部件的磨损，同时由于在1挡行驶，车速的控制可通过节气门的深浅进行控制，因此减小了制动次数。

图11 分层修正控制挡位图

(2)一般拥堵工况

车辆处于一般拥堵工况时，采用独立换挡控制策略的挡位如图12所示。

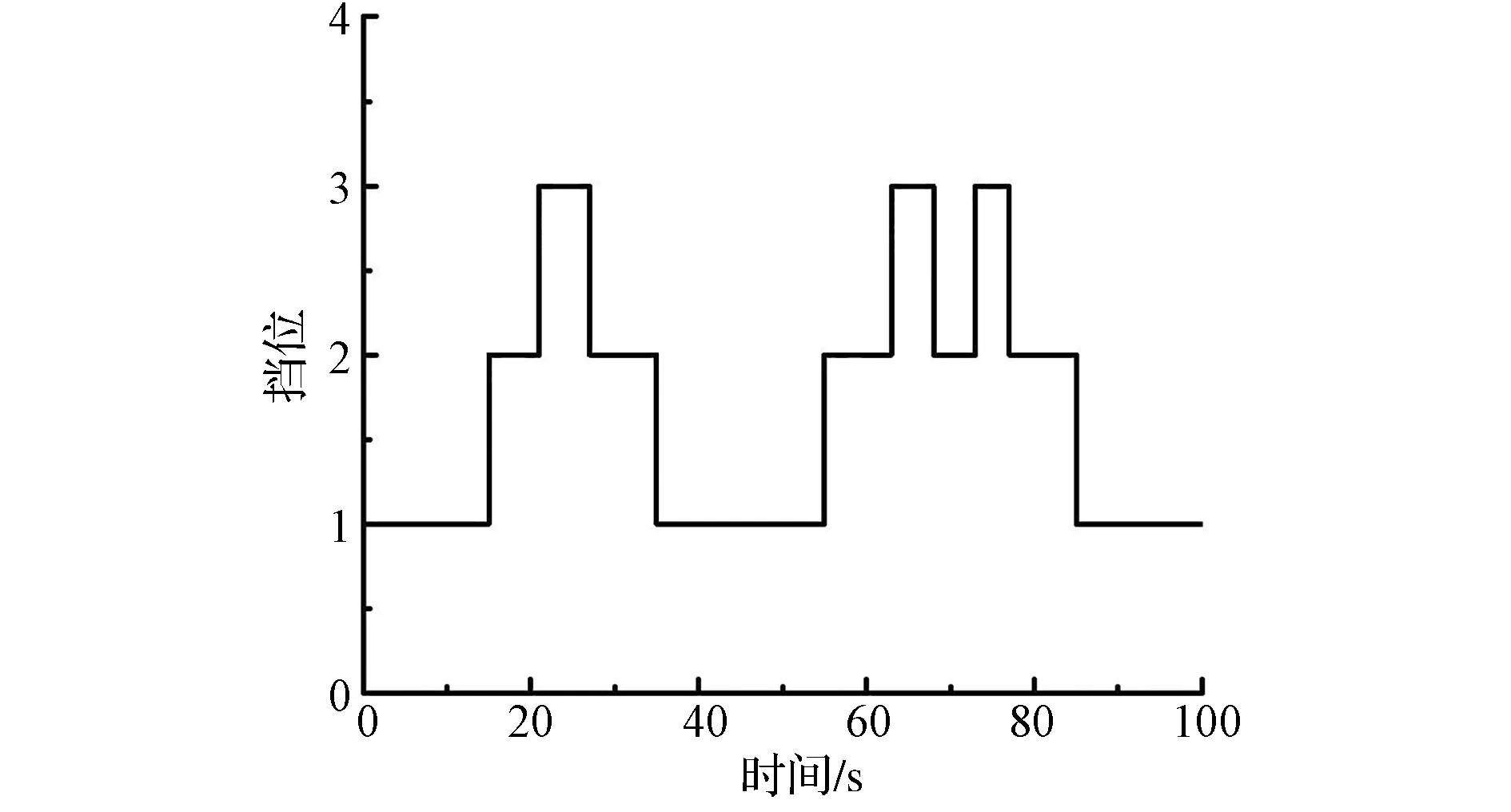
图12 独立控制挡位图

由图可见：车辆1挡行驶，此时车辆节气门开度低，车速低；当前方车辆加速时，驾驶员为了跟车，增大节气门开度，当达到基本换挡规律1挡升挡点时，车辆挡位升为2挡；随着车速的继续增加，当达到基本换挡规律2挡升挡点时，车辆挡位升为3挡；当前方车辆减速时，驾驶员为了行车安全，利用制动踏板减速，此时车速减小，当达到基本换挡规律3挡降挡点时，车辆挡位由3挡降为2挡；随着制动的持续，当达到基本换挡规律2挡降挡点时，挡位再降至1挡，这种频繁的升降挡一直持续到拥堵结束。

采用拥堵辨识换挡分层修正控制策略的挡位如图13所示。

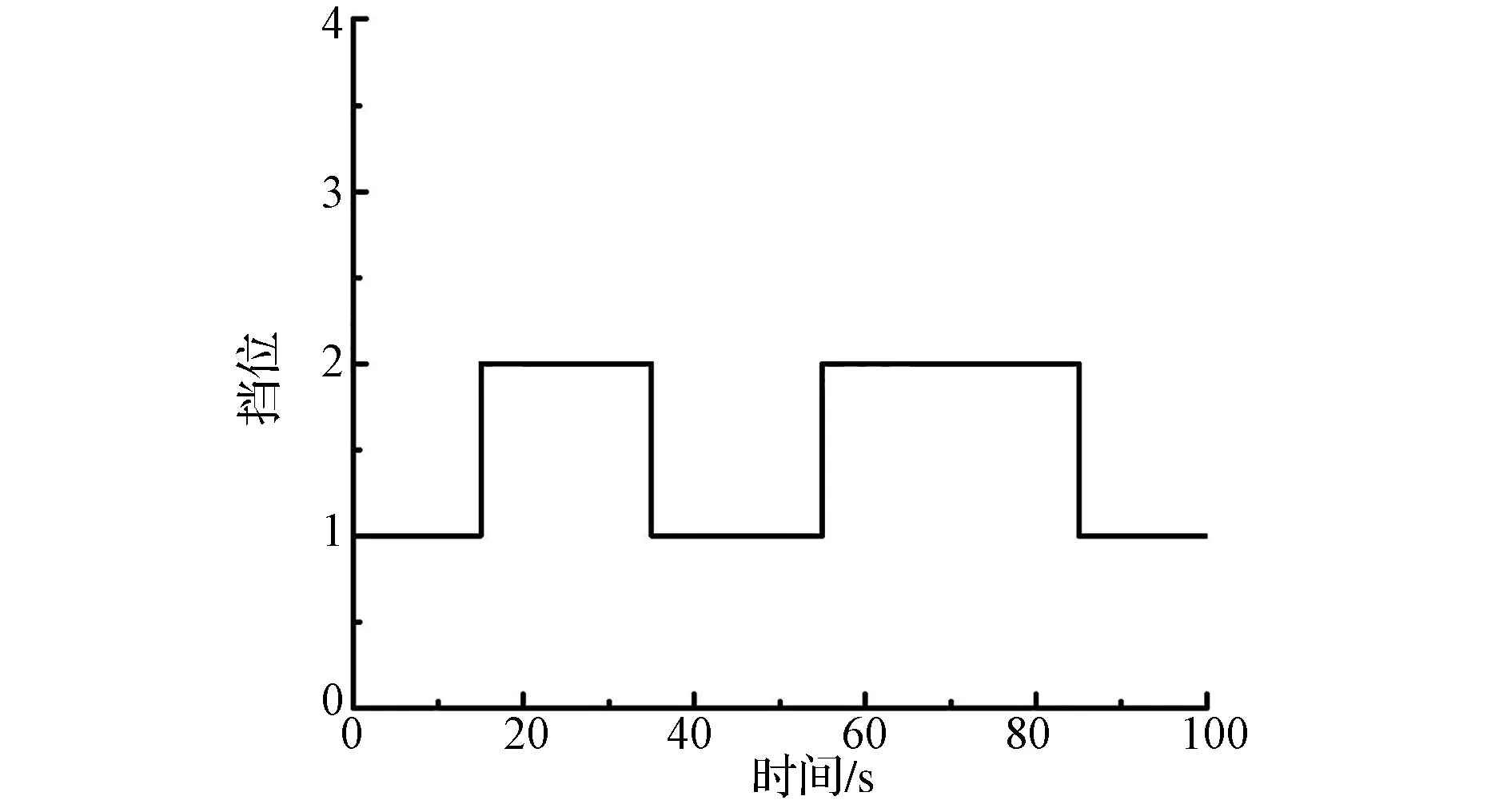
图13 分层修正控制挡位图

由图可见：车辆以1挡行驶，此时车辆节气门开度小，车速低；当前方车辆加速时，驾驶员为了跟车，增大节气门开度，当达到基本换挡规律1挡升挡点时，车辆挡位升至2挡；随着车速的增加，当达到基本换挡规律2挡升挡点时，车辆挡位应升至3挡，但是T-S模糊神经网络识别的拥堵工况为一般拥堵，根据一般拥堵工况的换挡修正策略，需要限制车辆升为3挡，保持2挡行驶；当前方车辆减速时，驾驶员为了行车安全，利用制动踏板减速，此时车速减小，当达到基本换挡规律2挡降挡点时，车辆挡位降至1挡；这样大大减少了换挡次数，降低了换挡部件的磨损，提高了车辆平顺性。

车辆处于拥堵工况，当采用独立换挡控制策略时，车辆由于节气门与速度的频繁变化，产生频繁升降挡现象，加剧了传动系统换挡机构零件的磨损，同时车辆平顺性变差；当采用换挡分层修正控制策略时，通过限制升挡，车辆始终维持在低挡位行驶，频繁升降挡现象消失。

6 实车试验

6.1 拥堵工况辨识与换挡修正系统搭建

搭建的拥堵工况辨识与自动变速换挡修正系统如图14所示。

由图可知，拥堵工况辨识与自动变速换挡修正系统由拥堵工况辨识样本采集模块、T-S模糊神经网络辨识模块、换挡修正模块和电磁阀驱动模块组成。

拥堵工况辨识样本采集模块如图15所示。

拥堵工况辨识样本采集模块采用NI CRIO 9036采集节气门开度(模拟信号)、制动踏板(数字信号)、车速(频率信号)和挡位(数字信号)传感器的输出信号，并进行信号调理，获得拥堵工况辨识样本，并发送至T-S模糊神经网络辨识模块。

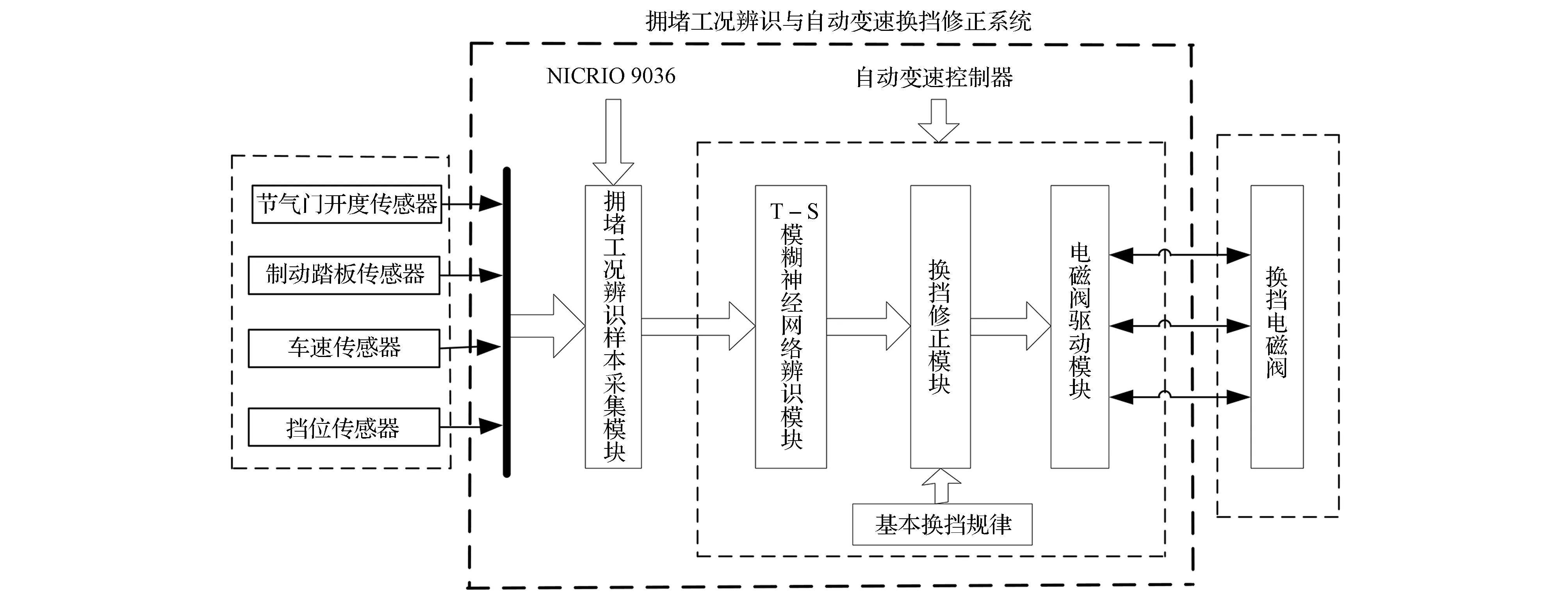
图14 实车试验原理图

图15 拥堵工况辨识样本采集模块

拥堵工况辨识样本采集模块软件部分是基于LABVIEW设计的，软件界面如图16所示，程序框图如图17所示。

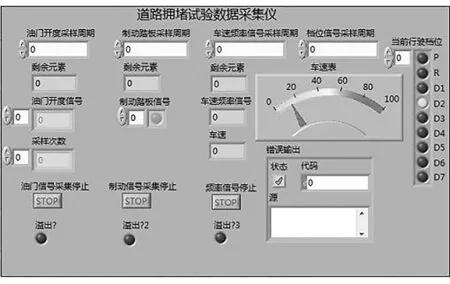
图16 上位机信号采集软件界面

图17 上位机信号采集软件程序框图

T-S模糊神经网络辨识模块对接收的拥堵工况辨识样本进行拥堵工况辨识，并将辨识结果发送至换挡修正模块。

换挡修正模块根据拥堵工况换挡修正策略，对基本换挡控制规律进行修正，并输出修正挡位至电磁阀驱动模块。

电磁阀驱动模块根据修正挡位输出驱动信号至换挡电磁阀，完成换挡修正。

6.2 试验验证

为验证所设计的拥堵工况辨识与自动变速换挡修正系统的有效性，本文中使用试验车辆进行实车道路试验。试验中，驾驶员按照“合肥南一环路-宁国南路-九华山路-马鞍山路-南一环路”的试验行车路线，选取工作日17：30-19：30进行试验，并记录相应的车速信号和挡位信号。由于整体试验数据过大，选出具有代表性的非常拥堵工况和一般拥堵工况试验数据进行分析。

(1)非常拥堵工况

当采用独立换挡控制策略时，采集的试验信号如图18所示。

图18 独立控制时车速与挡位信息图

由图可见，当采用独立换挡控制策略时，车辆低速行驶，驾驶员为了跟车与行车安全，频繁踩踏节气门踏板和制动踏板，导致挡位在1挡和2挡之间变化，频繁升降挡现象一直存在，乘坐舒适性变差。

当采用换挡分层修正控制策略时，采集的试验信号如图19所示。

由图可见，当采用换挡分层修正控制策略时，拥堵工况辨识样本经过自动变速控制器处理，辨识出车辆处于非常拥堵工况，按照制定的换挡修正控制策略，通过限制升挡车辆以1挡行驶，车辆没有出现频繁升降挡现象，车辆的乘坐舒适性得到提升。

(2)一般拥堵工况

当采用独立换挡控制策略时，采集的试验信号如图20所示。

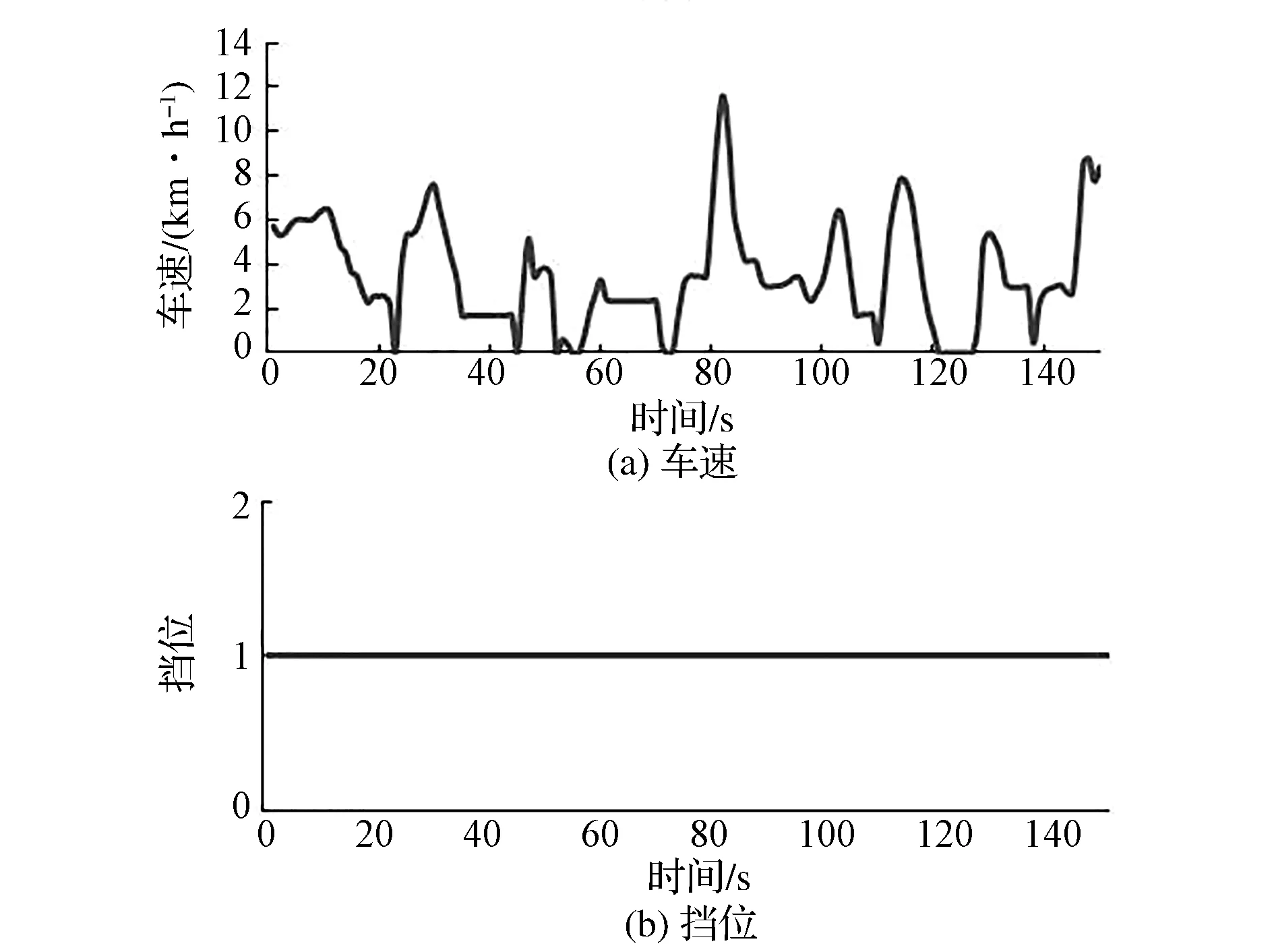
图19 分层修正控制时车速与挡位信息图

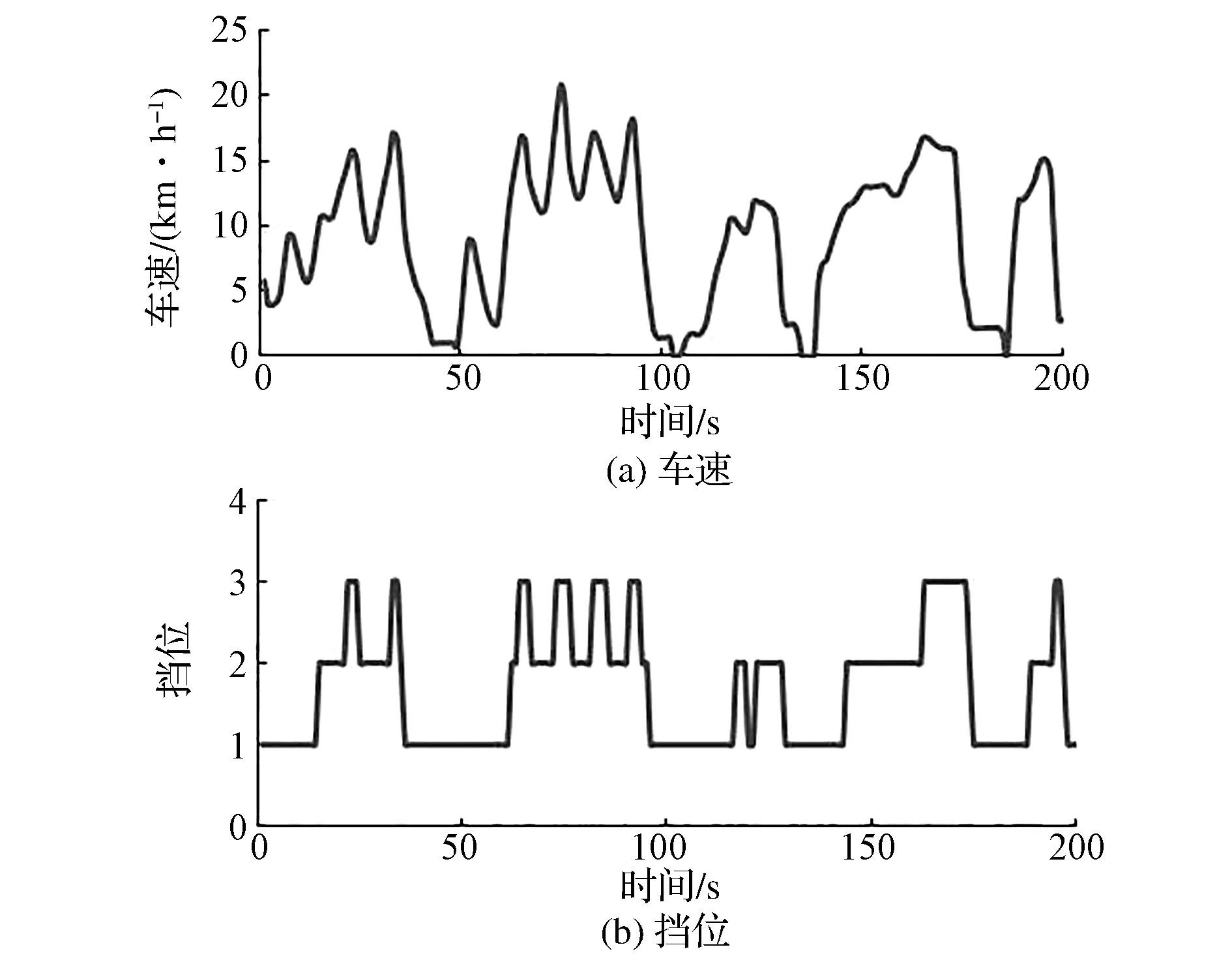
图20 独立控制时车速与挡位信息图

由图可见：当采用独立换挡控制策略时，车辆正常跟车行驶，前方车辆加速时，驾驶员为了跟车，加大节气门开度，当达到基本换挡规律1挡升挡点时，车辆挡位升至2挡；继续加速，当达到基本换挡规律2挡升挡点时，车辆挡位升至3挡；当前方车辆减速时，驾驶员为了行车安全，利用制动踏板减速，此时车速减小，当达到基本换挡规律3挡降挡点时，车辆挡位由3挡降至2挡；继续制动，当达到基本换挡规律2挡降挡点时，车辆挡位再由2挡降至1挡，频繁升降挡现象一直存在，乘坐舒适性变差。

当采用换挡分层修正控制策略时，采集的试验信号如图21所示。

由图可见，当采用换挡分层修正控制策略时，拥堵工况辨识样本经过自动变速控制器处理，辨识出车辆处于一般拥堵工况，按照制定的换挡修正控制策略，通过限制车辆2挡升为3挡，大大减少了换挡次数，降低了换挡部件的磨损。

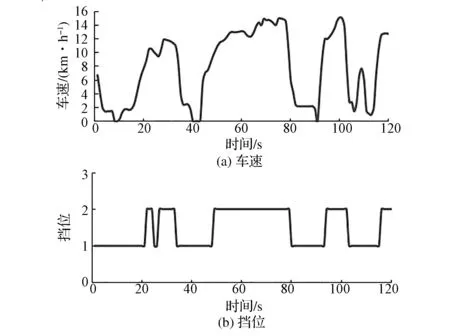
图21 分层修正控制时车速与挡位信息图

由一般拥堵与非常拥堵工况试验结果可知，基于T-S模糊神经网络可准确辨识车辆拥堵工况，基于拥堵工况辨识的换挡分层修正控制策略能够限制升挡，消除换挡循环，提高车辆平顺性与乘坐舒适性。

7 结论

(1)基于T-S模糊神经网络的拥堵工况辨识方法，选取车辆平均车速、平均节气门开度和样本时间内制动踏板作动次数为评价因子，建立T-S模糊神经网络，可准确辨识车辆所处的拥堵工况级别，为换挡修正分层控制策略提供判断依据。

(2)基于拥堵工况辨识的换挡修正分层控制策略，将车辆自动变速分为辨识决策层与换挡执行层，可有效避免频繁换挡，降低换挡部件的磨损。

(3)仿真与实车试验结果表明，当车辆处于拥堵工况时，拥堵工况辨识换挡修正分层控制策略可有效辨识拥堵工况并进行换挡修正，可有效消除频繁升降挡，提高车辆平顺性与乘坐舒适性。

参考文献

[1]史俊武.基于人-车-路系统的自动变速车辆智能换挡策略研究[D].上海：上海交通大学，2011.

[2]李萍.基于城市工况的汽车模糊巡航控制研究与仿真[D].锦州：辽宁工业大学，2014.

[3]朱丹丹.基于模糊综合评判的城际道路拥堵状态识别方法研究[D].长沙：中南大学，2013.

[4]YANGY，CUIZ，WU J，et al.Fuzzy c-means clustering and opposition-based reinforcement learning for traffic congestion identification[J].Journal of Information and Computer Science，2012(9)：2441-2450.

[5]GUI YAN J，LONG HUI G，JIANG FENG W.Traffic congestion identification method of urban expressway[J].Journal of Traffic and Transportation Engineering，2006，3：18.

[6]HAOY，SUNL，XU T，et al.Analysis of traffic congestion on urban expressway and congestion threshold identification[J].Journal of Tongji University(Natural Science)，2008(5)：9.

[7]高艺.基于一次拥堵的城市交通拥堵综合评价方法研究[D].北京：北京交通大学，2011.

[8]PERSAUD B N，HALL F L，HALL L M.Congestion identification aspects of the McMaster incident detection algorithm[J].Transportation Research Record，1990，1287.

[9]张炳力，王伦珍.双离合自动变速器特殊工况下换挡规律的智能在线修正研究[J].汽车工程，2015，37(6)：686-690.

[10]JIANMING H，QIANG M，QI W，et al.Traffic congestion identification based on image processing[J].IET Intelligent Transport Systems，2012，6(2)：153-160.

[11]李战明，王君，康爱红.基于T-S模糊模型RBF网络的自适应学习算法[J].兰州理工大学学报，2004，30(2)：82-85.

[12]朱大奇，史慧.人工神经网络原理及应用[M].北京：科学出版社，2006.

[13]李国勇.神经模糊控制理论及应用[M].北京：电子工业出版社，2009.

[14]张德丰.MATLAB模糊系统设计[M].北京：国防工业出版社，2009.

[15]刘拂晓，赵韩，江昊.纯电动汽车AMT换挡规律及仿真研究[J]. 合肥工业大学学报，2013，36(11)：1281-1284.