最小化CVaR对冲问题的随机分形搜索算法求解

李国成

(皖西学院 金融与数学学院，安徽 六安 237012)

在完全金融市场里，一个未定权益如期权所产生的风险可以通过构造标的资产和债券的投资组合来完全对冲[1]。但实际市场中由于随机波动率、跳跃以及交易的不连续性等因素的存在而使得市场是不完全的，未定权益的风险是不能被完全对冲掉的，而是部分对冲，通常采用平方对冲(Quadratic Hedging)。平方对冲方法虽然方法简单，但是具有显著的不足，即对”超额收益“加以惩罚[2]，这与实际投资者的需求是不一致。Föllmer和Leukert提出分位数对冲[3]，即在给定较小初始成本情形下通过最大化成功对冲概率来实现最优对冲。文献[4]的研究将该方法应用到一般的损失函数如期望损失最小化等。黄金波等研究采用最小化风险价值(Value-at-Risk, VaR)来获得最优对冲策略[5]。

但VaR作为风险的度量方法不具有次可加性和凸性，不是一致性的风险度量[6]。为此，Rockafellar和Uryasev提出一种改进的VaR[7]，即条件风险价值(Conditional Value-at-Risk, CVaR)。CVaR本身所具有的优点使得越来越多的学者和金融机构采用CVaR作为风险度量方式。近年来，CVaR在对冲问题中的应用研究也日益增多，如Topaloglou等构建了带有选择性对冲的CVaR模型用于国际资产配置研究[8]，Li和Xu基于CVaR风险度量建立带有收益上下界约束的动态对冲模型[9]，迟国泰等基于CVaR建立套期比优化模型并与最小方差套期比以及VaR套期比模型进行对比研究[10]，费广平和孙燕红基于CVaR最小建立最优股指期货套期比决策模型[11]，黄金波和李仲飞研究分布不确定下的风险对冲策略及其效用[12]。本文研究在考虑交易费用情形下和在给定初始成本约束条件下采用CVaR来刻画由期权到期时的支付和投资组合价值之间的不对等所产生的损失风险，建立动态随机优化模型，并探寻用随机分形搜索算法来求解该模型。

1 最小化CVaR对冲问题

1.1 问题描述

考虑金融市场上有风险资产(股票)和无风险资产(债券)来构造投资组合，进而形成对冲策略。设t时刻风险资产(股票)价格为St，服从跳-扩散模型，即满足以下方程：

(1)

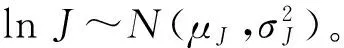
设债券(无风险资产)价格为Bt，满足以下方程：

(2)

假设投资期内具有T个离散决策点，投资者通过构造股票和债券的投资组合形成对冲策略，即投资者在t时刻持有θt的股票和δt的债券构成投资决策φt=(θt,δt)，该投资组合价值为Vt=θtSt+δtBt，其中t=0,1,…,T-1。则可知投资组合在期末价值为：

(3)

(4)

其中，V0为初始成本，H=max{ST-K,0}，K为期权的执行价格。若初始成本给定，则L(V0,Φ)简化为L(Φ)。且采用自融资策略，即∀t=1,2,…,T-1对冲策略Φ满足：

(5)

设Π为满足自融资条件的允许决策集，根据文献[7]可得期权卖出者期末的损失风险的条件风险价值为：

(6)

其中Fα(Φ,ξ)=ξ+(1-α)-1E[(L(Φ)-ξ)+]，这里(·)+定义为(x)+=max{x,0}。文献[7]进一步给出在模拟出离散价格数据yj,j=1,2,…,J的概率分布p(yj)的前提下，Fα(x,ξ)的近似计算为：

(7)

1.2 数学模型

设为交易费率f，则执行一个对冲策略Φ产生交易成本为：

(8)

由此可得到在给定初始成本V0和采用自融资策略的条件下带有交易费用的最小化CVaR的最优对冲策略的优化模型为：

(9)

如上式(9)所描述的最小化CVaR最优对冲模型是一个动态随机优化模型，其目标函数为非线性的且是不光滑的。为此，很多研究者借助于光滑方法来实现近似求解，取得了不错的效果[13，14]。本文探寻文献[15]所提出的随机分形搜索算法来实现最小化CVaR最优对冲模型的求解，进行模拟算例和实证研究，并和GA、PSO两种算法进行对比研究。

2 随机分形搜索算法

文献[15]基于分形的扩散性质提出新的元启发式搜索算法即随机分形搜索算法(Stochastic Fractal Search, SFS)，主要借助扩散和更新过程(包括两次更新)来实现求解全局优化问题。其算法步骤简述如下[15]：

Step 1 初始化算法的基本参数：粒子的数目N和相关参数等，设定迭代终止条件。

Step 2 随机生成每个粒子的初始位置Pi，并赋予相等的初始适应度。

Step 3 根据扩散过程，从式(10)和(11)所描述的两种高斯游走方式中随机选取一种执行，其中随机数ε～U(0,1)，BP为最好个体位置，μBP和μP分别代表相应的均值，标准差σ=|(Pi-BP)×log(g)/g|，其中g为迭代次数。

Step 4 计算每个粒子的概率值Pai=rank(Pi)/N，生成随机数ε，若Pai<ε，则按下式更新每个Pi，即实现首次更新，其中Pr和Pt是从种群中随机抽取的。

(12)

由此构建的启发式搜索算法SFS在“勘探”和“开采”两种能力上获得很好的平衡，具有较好的全局优化能力，对经典测试函数的测试结果表明其具有很好的优化性能[15]。因此，本文探寻用该算法来求解最小化CVaR对冲问题。

3 交叉熵蝙蝠算法求解最小化CVaR对冲问题的算法架构

3.1 个体构成

对冲策略是一个决策序列，每个决策点都有两个控制变量，因而随机分形搜索算法中种群的每个个体代表一个满足自融资条件的可行对冲策略Xi=(xi1,…,xi,T,xi,T+1,…,xi,2T,ξ)，本文考虑不允许卖空情形，因而每个分量都满足非负条件。其中ξ为阈值控制变量，前T个分量为投资者在t=0,1,…,T-1时刻所持有的股票的比重，后T个分量为其持有债券的比重。

3.2 适应度函数的表示

按照前文式(6)和式(9)所描述的最小化CVaR对冲问题的目标函数，随机分形搜索算法在具体求解该问题时用于评价个体优劣的适应度函数可定义如下：

(15)

3.3 约束的处理

本文基于自融资策略研究在非卖空条件下实现对欧式看涨期权的套期保值，约束条件如前文式(5)所描述及决策变量的非负性，考虑到无风险利率时相对稳定性的，因而可采用折现价格可将式(5)简化为：

(16)

其中t=0,1,…,T-2。本文采用拉格朗日乘子法引入惩罚因子Mi将约束优化转化为无约束优化，即在式(16)所表示的适应度函数中加入如下惩罚项：

(17)

其中，惩罚因子Mi为非常大的正数。

4 数值实验和结果分析

4.1 模拟算例

设卖出的欧式看涨期权的期限分别为3，6，9和12月，通过构造标的资产和债券的组合资产来进行套期保值，采用CVaR度量期权风险，以对冲成本与CVaR之和最小化为优化目标来寻求最优动态对冲策略。每周决策1次，一年以52周计；如前所述的跳-扩散参数μ、σ、μJ、σJ和λ分别设为0.01、0.2、0.1、0.2和10，设初始价格S0=100元，敲定价格K=85元，模拟生成100条价格路径进行测试。同时，假设同期的活期存款年利率为r=0.4%。

图1 100条模拟股票价格路径

为了便于对比分析，本文分别用GA、PSO和SFS三种算法求解基于100条模拟股票价格路径数据的自融资条件下带有交易费用的最小化CVaR最优动态对冲模型，初始成本V0=10元，交易费率按0.2%收取，三种算法的求解结果如表1所示。其中，期权风险采用CVaR度量，因初始成本V0固定，故对冲费用仅为执行对冲策略所支付的交易费，总和即为风险和对冲费用之和；这三个指标均为劣指标，即其值越小越好，三种算法求解结果对比胜出者以粗体标识。

表1 模拟算例的动态对冲结果

从表1可以看出对四种欧式看涨期权执行SFS所获得的对冲策略的对冲效果都是最好，其对应的条件风险价值都是最小的，对冲总费用也是最低的，其次是GA，PSO所求得的策略对冲风险能力最差，对冲成本和风险之和也最大。模拟算例结果表明SFS算法求解最小化条件在险价值最优对冲问题是可行的，且取得了不错的对冲效果。

4.2 实证研究

本节借助实证分析研究来进一步验证SFS算法在求解最小CVaR最优动态对冲问题时的可行性和有效性，选用2014年1月2日至2016年6月31日的上证综合指数的日收盘价数据共计642个样本数据，具体变化趋势如图2所示。指数初始价格为S0=1 209.4，无风险利率为r=0.35%。期权期限T为四个不同的到期时间，其敲定价格K也设置为四种不同价格，具体见表2，分别采用GA、PSO和SFS求解，其结果如表2所示。其中胜出者以粗体标识。

图2 2014—2016年上证综合指数的日收盘价数据

T/周K 风险(CVaR) 对冲费用 总和 GAPSOSFSGAPSOSFSGAPSOSFS1311001424.291470.991342.897.0816.401.101431.371487.391343.8912001243.371252.041214.637.0617.241.061250.431269.281215.6913001163.821141.651077.989.1115.991.171172.931157.641079.1514001000.41089.45998.228.0216.160.901008.421105.61999.122615001005.081018.061018.0210.5431.341.381015.621049.401019.401600996.071061.08915.8510.5333.321.291006.601094.40917.131700935.81969.01853.4910.5231.581.16946.331000.59854.651800747.84723.28691.9711.2129.461.53759.05752.74693.51391900820.44885.04794.9415.6951.931.87836.13936.97796.812000666.41748.47654.2916.5045.311.80682.91793.78656.082100667.7681.69585.9214.7649.691.73682.46731.38587.652200546.38574.87533.7714.9047.931.85561.28622.80535.63522300612.15678.72604.8222.3278.422.60634.47757.14607.422400586.92644.93585.5921.9563.882.52608.88708.81588.112500521.59542.00517.3919.8860.892.08541.47602.89519.472600504.83540.11468.2720.0654.732.28524.89594.84470.55

从表2的对冲结果可以看出SFS对冲的效果最好，风险、对冲费用和总和三个指标值都是最小的，其次是GA，PSO的表现最差。同时，表2也再次表明本文SFS算法求解CVaR最优动态对冲问题是可行和有效的，可以使得投资者以较少的对冲成本完成现套期保值，进而较小风险，具有重要的实际意义。

为了进一步研究初始成本对期权风险或对冲总费用的影响，本文以数据集S1(即J=100时的模拟数据)为例，并设定敲定价格K=2000元，利用SFS算法分别求出初始成本从100元以100元等距递增到3000元共计30种不同初始成本对应的风险(CVaR)和总和(风险和对冲费用之和)，并绘制出风险和总和随初始成本变化而变化的趋势图，如图3所示。

从图3可以发现，期权风险即CVaR随着初始成本的增加而减少，并且当初始成本足够大时(大于3000元时)，风险几乎为零；风险和对冲总费用的总和也随着初始成本的增加而减少，并且当初始成本足够大时(大于1800元时)，总和基本保持平稳，这表但对于期权的出售者而言，若从风险(CVaR)和对冲总费用(包括初始成本V0)两方面综合考虑，则并不是初始成本越大越好，而是可以选取恰当的初始成本可以使得总和最小，即所承担的风险和对冲总费用之和最小。

图3 初始成本-风险(CVaR)/总和的变化曲线

5 结论

本文在给定初始成本的条件下考虑带有交易费用和不允许卖空的情形，基于自融资策略，以CVaR来度量期权的风险，最小化CVaR和对冲成本之和为优化目标，建立动态对冲优化模型，该模型目标函数不可微，因而经典的基于梯度的优化算法已不再适用该模型的求解，同时，由于情景数和约束条件个数均较多，线性规划方法求解成本很高，因而本文通过个体构成、适应度函数的表示的实现和自融资约束条件的处理，用随机分形搜索算法来实现该模型的求解，借助模拟算例和实证分析两个测试实验来检验SFS算法求解这个随机优化问题的可行性和有效性，并与GA和PSO两种算法进行对比，结果表明SFS算法所获得的动态对冲策略的实际对冲效果是最好的，不仅是可行的，还取得了很好的实际应用效果。

参考文献：

[1]Merton R C. Option Pricing When Underlying Stock Returns Are Discontinuous[J]. Journal of Financial Economics, 1976(3): 125-144.

[2]Schweizer M. A Guided Tour Through Quadratic Hedging Approaches[C]//Jouini E et al. Option Pricing Interest Rates and Risk Management. Cambridge: Cambridge University Press, 2010: 538-574.

[3]Föllmer H, Leukert P. Quantilehedging[J].Finance and Stochastics, 1999, 3(3): 251-273.

[4]Föllmer H, Leukert P. Efficient Hedging: Cost Versus Shortfall Risk[J]. Finance and Stochastics, 2000, 4(2): 117-146.

[5]黄金波，郑军，丁杰，等.VaR测度下的风险对冲策略研究[J].运筹与管理，2017，26(3)：138-147.

[6]Morgan J P. RiskMetrics Technical Document [M].4thed. New York: Morgan Guaranty Trust Company, 1996.

[7]Rockafellar R T, Uryasev S. Optimization of Conditional Value-At-Risk[J].Journal of Risk, 1999, 29(1):1071-1074.

[8]Topaloglou N, Vladimirou H, Zenios S A. CVaR Models with Selective Hedging for International Asset Allocation[J].Journal of Banking & Finance, 2002, 26(7):1535-1561.

[9]Li J, Xu M. Risk Minimizing Portfolio Optimization and Hedging with Conditional Value-at-risk[J].Review of Futures Markets 2008(16):471-506.

[10]迟国泰，赵光军，杨中原.基于CVaR的期货最优套期保值比率模型及应用[J].系统管理学报，2009，18(1)：27-33.

[11]费广平，孙燕红.最小CVaR股指期货套期保值比率的实证研究[J].统计与决策，2013(8)：156-159.

[12]黄金波，李仲飞.分布不确定下的风险对冲策略及其效用[J].中国管理科学，2017，25(1)：1-10.

[13]Tarnopolskaya T, Zhu Z. CVaR-minimising Hedging by a Smoothing Method[J]. Anziam Journal, 2010, 52(C):237-256.

[14]张清叶，高岩.基于CVaR投资组合优化问题的非光滑优化方法[J].中国管理科学，2017(10)：11-19.

[15]Salimi H. Stochastic Fractal Search: A Powerful Metaheuristic Algorithm[J]. Knowledge-Based Systems, 2015(75):1-18.

Abstract: In this paper, based on the jump diffusion model, we consider the problem of hedging conditional value at risk of contingent claims on a stock under transaction costs and given initial cost. A dynamic stochastic optimization model is established, and Stochastic Fractal Search is used to solve the nonlinear optimization problem to obtain the optimal hedging strategy. The results of numerical simulation and empirical research show that Stochastic Fractal Search is feasible and effective for solving the hedging problem by minimum CVaR.

Keywords: hedging; conditional value at risk; jump diffusion model; stochastic fractal search