初中几何教学中“中点”问题的解题策略及案例

张凤琴

（宁波市鄞州区横溪镇中学）

当我们解决几何问题时，构造辅助线，找到中点、中心、重心的位置，分析线段比例等，都能够帮助我们很好地分析和解决问题。运用好“中点”这一要素，可以帮助我们快速地抓住要点，更快更准地完成答题任务。

一、见“中点”，要分析

（一）考虑中位线

在三角形中解决几何问题时，如果已知一边中点，第一步要考虑找到另一条边的中点，将两点连线，这条线便是该三角形的中位线。中位线的特点是，平行并等于第三条边的一半。

比如下面这道例题：

已知三角形ABC中，点D是线段AB的中点，点E是线段AC的中点，证明

（分析：由题可知点D和点E分别是线段AB和线段AC的中点，所以线段DE是三角形ABC的中位线，所以线段BC的长度等于两倍线段DE的长度。）

解：∵D和E分别是AB和AC的中点

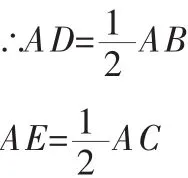
且∠DAE=∠BAC

∴△ABC∽△ADE

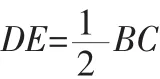
综上

图1

（二）特殊三角形首先考虑中线

当结题时遇到特殊的三角形，如直角三角形、等腰三角形、等边三角形、等腰直角三角形等图形时，首先找到特殊边的中点。例如：找到直角三角形斜边中点，将这个中点与直角的顶点相连，这条线为斜边中线，长度为斜边的一半。

图2

例题：如图2所示，△ABC为直角三角形，D为AB的中点，AC长为3cm，DC长2.5cm，求BC长度。

（分析：首先证明出直角三角形斜边中线为斜边的一半，再利用勾股定理求出BC长度。）

方法一：

图3

解：如图3所示，延长CD，使DE=CD。连接AE，EB

∵D是AB中点，CD是AB上的中线

∴AD=DB

∵CD=DE

∴四边形ACBE是平行四边形

∵∠ACB=90°

∴平行四边形ACBE是矩形

∴AB=CE，AD=BD，CD=DE

∴AD=BD=CD=DE

∴AB=2CD=5cm

∵AC2＋BC2=AB（2勾股定理）

∴BC2=52-32

BC=4cm

答：BC长为4厘米。

方法二：（分析：利用三角形全等定理证明CD=1AB，再通过

2勾股定理算出边长。）

图4

解：如图4，过B点做一条垂直于BC的直线与CD延长线交于E点

∵∠ACB=∠EBC=90°

∴AC∥BE（同旁内角互补，两直线平行）

∴∠CAB=∠ABE

在△ACD和△BDE中

∠CAB=∠ABE

D是AB中点

∴AD=DB

∠ADC=∠EDB

∴△ACD≌△BED（ASA）

∴AC=EB，CD=ED

∴在△ACB和△EBC中

AC=EB

∠ACB=∠EBC

CB=BC

∴△ACB≌△EBC（SAS）

∴∠DCB=∠ABC

∴CD=BD=AD

∵AB=2CD=5cm

∵AC2＋BC2=AB2（勾股定理）

∴BC2=52-32

BC=4cm

答：BC长为4厘米。

特殊的三角形：等腰三角形的三线合一定理

（分析：利用三角形的全等知识，证明出等腰三角形的三线合一定理，从而解决相关问题。）

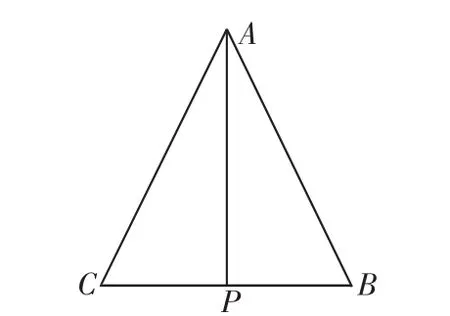
图5

例题：如图5所示，△ACB为等腰三角形，P为CB中点，AB＝5cm，AP＝4cm，求BC的长度。

解：∵P是CB中点

∴CP＝PB

∵△ACB是等腰三角形

∴AC＝AB

∠C＝∠B

AP是△ACP和△APB的公共边

∴△APB≌△ACP

∠CAP＝∠PAB

∴AP⊥CB（三线合一定理）

∠APB＝90°

∴△ACP和△APB是直角三角形

根据勾股定理可知，

PB2＋AP2＝AB2

∵AB＝5cm，AP＝4cm

∴PB＝3

∵P是CB中点

BC＝6cm

答：综上，BC边长为6厘米。

（三）做出以此中点为对称中心的对称图形。

图6

例题：如图6，△ACB为直角三角形，D为AB边上的中点，以D为中心，做△ABC的中心对称图形ABE。连接DE。因为中心对称，所以△ABC≌△ABE。由此可知 AC＝EB，AE＝CB，AD＝DB＝CD＝

综合上述条件可以得出边长关系，以便解决其他问题。

（四）一般的四边形中点问题，可以转化为三角形中线，中位线定理的应用，也就是连接一条对角线并找到它的中点。

二、创新型几何教育教学工作的开展

教师在课堂教学时就要努力引导学生的思维，将那些学习有困难的学生拉入课堂讨论中，提高他们的课堂参与感，从而激发他们学习的热情。课下，也可以针对不同学习程度的学生进行有针对性的指导，在家庭作业方面可以对基础较薄弱的学生进行单独的讲解，并留一些适合他们练习的题目。因材施教的方法让不同程度的学生都能根据自己的理解能力，掌握几何学习的节奏，从而帮助他们理解记忆，以便更好地提高成绩。

在几何教学中要注重几何语言的应用。图形语言、文字语言及符号语言是几何语言的三种存在形式。老师不仅要锻炼学生建立三种几何语言的能力，还要培养其将三种语言相互转化，并且适当运用的能力。因为三种语言的特点不尽相同，所以在几何教学中也都各自发挥着不同的作用。例如图形语言比较直观，其形象生动的特质能帮助学生更好地认识和理解相关问题；文字语言就比较抽象，不是那么容易理解，但是其概括性很强，可以对图形本身和其中蕴含的条件进行准确的描述与解释，并且对几何的定理、公式、定义等内容进行精确的表达，使学生能充分理解题目，加快做题进度，节省时间。符号语言是文字语言的又一次简化，更加抽象，因此符号语言也是三种语言中最难掌握的一种。它对于几何学习的初学者的逻辑推理能力要求相对较高。因此教育工作者在教学过程中，要抓住时机针对学生对这三种语言相互转化方面的意识和能力进行训练和提升。

在几何学习中什么是证明？经过分析推理出一个命题的正确性，这个逻辑推理的过程也就是我们所说的证明。那“推理过程”又是什么呢？解决具体问题时我们又该如何引导学生进行“推理”呢？

正所谓“授之以鱼，不如授之以渔”，教师所能教授的只是理论，只有学生自己拥有清晰的解题思路，掌握解题方法，才能做到举一反三，游刃有余地解决问题。因此教师要讲解寻找证明思路的方法。几何学习中比较常用的解题方法是分析综合法。也就是把所学证明方法进行综合运用来论证命题的一种思维方式。从不同角度出发考虑问题，在解决较难问题时，会收到事半功倍的效果。

几何作为一门严谨的学科。首先在学习态度上就要端正。几何推理证明能力的养成是很漫长、很艰难的过程。不论是老师或是学生都不要操之过急，要有计划性、有针对性地去学习。从简单到复杂，由浅入深，使学生由被动学习变成主动学习。针对一些重难点，例如中点、重心、中位线等，要更加注重教学模式的改革，为学生打好基础。

参考文献：

张顺燕.数学的源与流［M］.北京：高等教育出版社，2004.