结合多尺度时频调制与多线性主成分分析的乐器识别
王 飞,于凤芹
(江南大学 物联网工程学院,江苏 无锡 214100)
0 引言
乐器识别作为音乐信息检索(Music Information Retrieval, MIR)的一部分,可用于对音乐的自动标注、音乐分类、音乐情感识别[1]。
已有乐器识别模型基于四大特征:倒谱特征、时域频域特征、稀疏特征、概率特征。文献[2]使用改进的梅尔倒谱系数(Mel-Frequency Cepstral Coefficient, MFCC)特征结合主成分分析(Principle Component Analysis, PCA)降维进一步提高乐器识别准确率,但MFCC对乐音谐波特征描述不足且对无明显共振峰的打击乐器识别较差。文献[3]从时域、频域对乐器提取特征从而获得稳定的识别,但乐器音色并非只是时域或频域的[4]。此外,特征的组合依赖训练集,不同的训练集拥有不同的最佳特征。文献[5]利用稀疏倒谱编码对单、多声部乐器识别比现有方法更精确;文献[6]首次使用稀疏过滤进行单声部乐器识别,但稀疏特征忽略了时域信息。概率特征是乐器识别的另一研究方向:文献[7]提出一种可在单声道多声部音乐中同时识别乐器类型和估计音阶的概率混合模型;文献[8]对多声部音乐的频谱结构提出不变最大高斯包络(Uniform MAx Gaussian Envelope, UMAGE);文献[9]针对乐器二分类问题利用概率潜在模型(Probabilistic Latent Component Analysis, PLCA)对乐器的声谱进行建模,但它们需先验启奏时间与乐器数量的前提假设。
从听觉角度看,人耳处理声音信号的本质是耳蜗将声信号频率分解转换成听觉表示,随后传入初级听觉系统进行多尺度时频调制[10]。耳蜗输出的听觉表示称为听觉谱图(Auditory Spectrum, AS)[11],听觉谱图包含乐器时频信息。利用多尺度时频调制对听觉谱图进行时间与频率维度的多分辨率滤波分解以获取乐音时频变化信息,这些时频变化信息是乐器音色的表示,利用这些表示可进行乐器识别。由于时频调制特征是冗余的多维数组,若使用PCA对多维数组降维会破坏特征结构,因此本文使用多线性主成分分析(Multilinear Principal Component Analysis, MPCA)对其降维以保留特征内在相关性,降维后的特征被送入支持向量机(Support Vector Machine, SVM)进行识别。本文首先提取萨克斯管、大号、长笛、吉他、钢琴、小提琴等9种乐音的听觉谱图并利用多尺度时频调制获取乐音的时频信息,随后利用MPCA对时频信息降维,最后利用支持向量机进行乐器识别研究。
1 基本原理
1.1 听觉谱图
听觉谱图是耳蜗模型的输出,乐音经过基底膜滤波、侧抑制作用、外毛细胞滤波后生成听觉谱图。它包含乐音的谐波随时间变化信息,相比语谱图更接近人耳对声信号的感知且冗余度更低,这有利于多尺度时频调制获得乐音的时频变化。耳蜗模型由基底膜模型和外毛细胞模型两部分组成[12]。
1)基底膜模型。基底膜模型利用Gammatone带通滤波器组将乐音s(t)分解为多个对应中心频率不同的通道,每个通道包含乐音的谐波成分随时间变化的信息。为提高对乐音中高频的分辨率,本文增加Gammatone带通滤波器组h(t;s)至128个,其中心频率s覆盖8.6个倍频程(62.5~20 kHz),可表示为:
y1(t;s)=s(t)*th(t;s)
(1)
其中:卷积符号下标*t表示对时间t进行卷积,s对应于滤波器组的中心频率。
2)外毛细胞模型。对滤波器组的通道进行差分,模拟侧抑制作用,紧接着使用积分窗来模拟神经元无法对快速变化的信号进行响应。整个过程可表示为:
y2(t;s)=∂sy1(t;s)*tμ(t;τ)
(2)
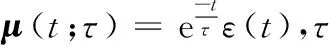
图1为钢琴和小提琴Bb5音符的听觉谱图:横轴表示时间,它含有某一频率随时间波动的信息;纵轴表示带通滤波器组的中心频率,它包含某一时刻频率信息。可以看出钢琴谐波衰减比小提琴更快,小提琴谐波比钢琴更丰富,所以听觉谱图包含了乐器时间与频率信息。
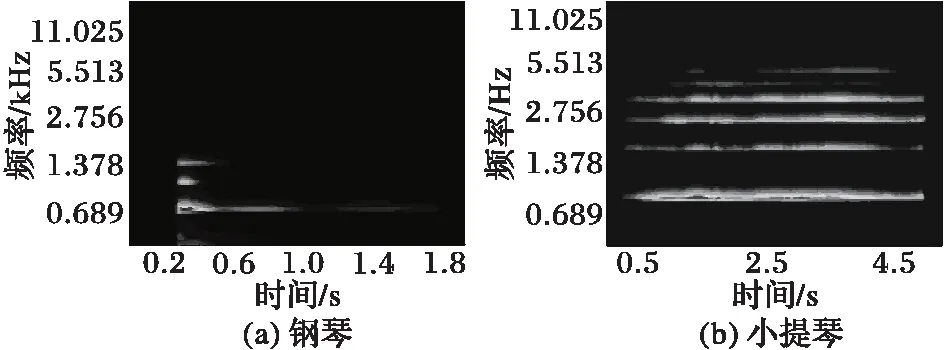
图1 钢琴与小提琴Bb5音符的听觉谱图 Fig. 1 Auditory spectrum of piano Bb5 and violin Bb5
1.2 多尺度时频调制
听觉谱图包含乐音信号谐波随时间变化的信息,对听觉谱图多尺度时频调制可以获取乐音信号的时频特征。所谓时频调制,就是时域调制和频域调制的组合,其中时域调制反映包络沿时间轴的波动,频域调制则描述声谱沿频率的起伏。多尺度是为了对不同分量进行“筛选”并细致观察。
多尺度时频调制为一组沿频率和时间轴抽取调制信息的滤波器组,其输出为四维数组:
r(t,s;Rc;Ωc)=y2(t;s)*t,s(g(t;Rc)·h(s;Ωc))
(3)
其中:g(t)=t3e-4tsin 2πt表示对时间维度上的滤波,h(s) = (1-2(πs)2)e-(πs)2表示对频率维度上的滤波。g(t;Rc)=Rcg(tRc),h(s;Ωc)=Ωch(sΩc)相当于一系列等品质因数带通滤波器。卷积符号下标*t,s表示对变量t与s进行卷积。
从小波角度来看,时间尺度Rc使得g(t)能够在不同尺度下去观测乐音不同频率随时间的变化,频率尺度Ωc使得h(s)在不同尺度下去观测乐音频率成分的变化。因此,调制输出与音色感知是直接相关的。本文中时间尺度Rc选取为±25,±24.5,…,±20.5共计18个,频率尺度选取为2-2,2-1.5,…,23共计11个,t可视为平稳而平均,因此时频调制的输出可用三维数组r(s,Rc,Ωc)表示。
图2分别为小提琴和钢琴Bb5音符的时频调制输出,颜色越亮幅值越高。为便于观察,将时频调制输出分别对s、Rc和Ωc平均后得图2(a)~(c)。由于小提琴比钢琴具有更多明显的谐波成分,小提琴比钢琴在图2(b)与图2(c)中具有更多的谱线。Ωc越大对应信号中频率越高的成分,图2(b)含谐波的变化信息。图2(c)描绘同一时刻不同频率成分的变化情况,Rc值越大对应频率成分变化越剧烈,它表明了小提琴和钢琴频率成分随时间变化的信息。图2(a)则表明多时间频率尺度下乐音的响应,不同的乐音具有不同的响应,因此多尺度时频调制输出可以作为乐音音色表示。
1.3 多线性主成分分析算法
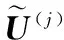
(4)
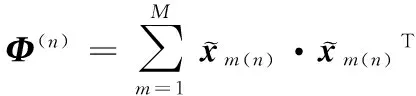
(5)
利用局部最优化的投影矩阵可得维度更小的张量ym:
(6)
投影矩阵将张量xm投射到维度更小的张量ym,在不破坏数据结构的情况下实现了降维。
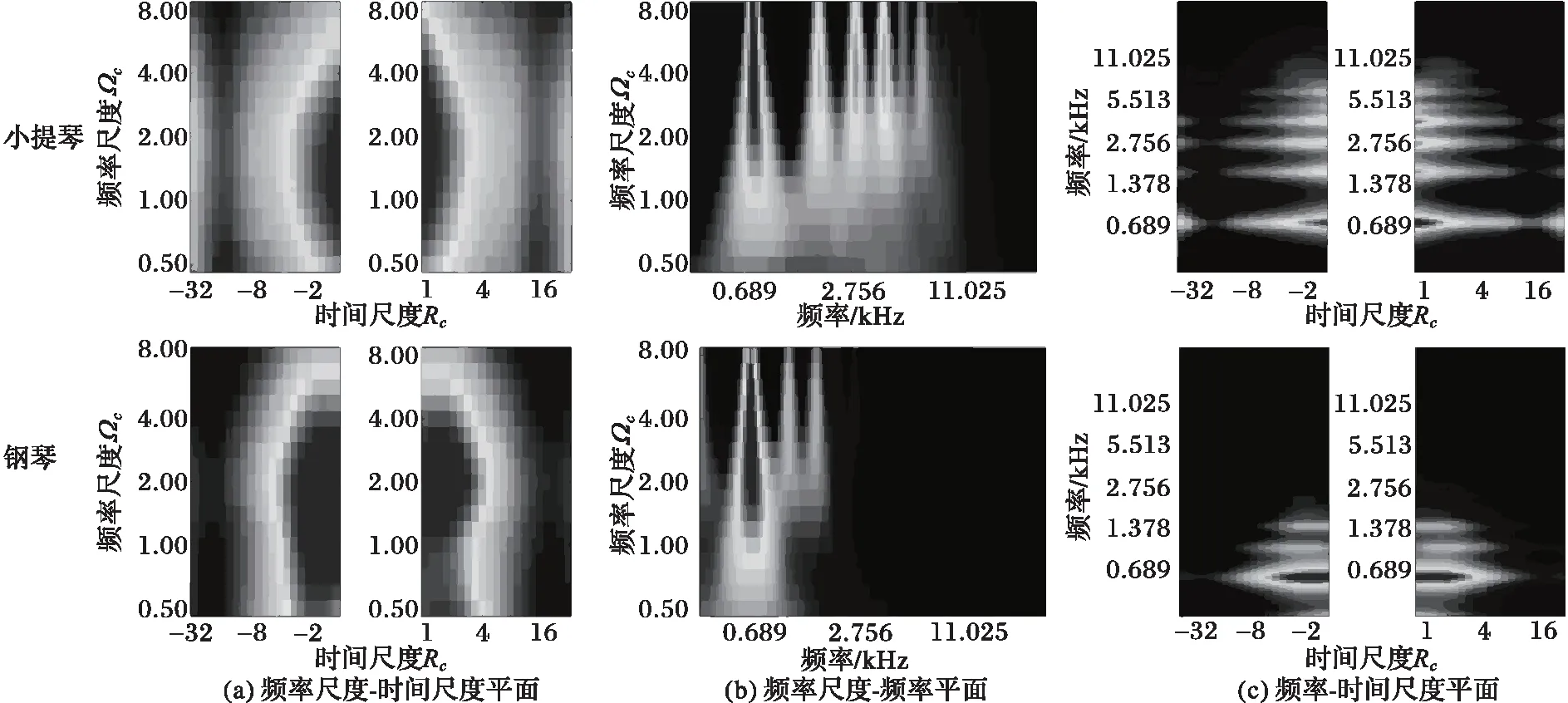
图2 小提琴和钢琴多尺度时频调制输出 Fig. 2 Multiscale time-frequency modulation output of violin and piano
2 实现步骤
本文采用10折交叉验证来确定乐器识别的准确率。基于多尺度时频调制的乐器识别具体步骤如下:
1)将样本库中每类样本随机等分10份,任选9份作为训练集,剩余1份作为测试集。
2)使用耳蜗模型获取听觉谱图。
3)使用多尺度时频调制对听觉谱图分解,获取时频调制特征r(s,Rc,Ωc) 。该特征为128×18×11维的张量。
4)利用MPCA算法对训练集的时频调制输出进行降维并获取张量各模态的投影矩阵,降维并保留98%的方差得到10×3×2维的降维后的张量,将张量展开为60维向量作为SVM的分类器训练输入。
5)重复步骤1)和2)提取测试集中的多尺度时频调制特征,用步骤3)得出的各模态的投影矩阵对测试集特征进行降维,选取同样的60维主成分作为测试集的SVM分类器输入。
6)从样本库中重新选1份作为测试集,其余9份作为训练集,重复步骤2)~4),共计10次,直到训练和测试覆盖整个乐音的样本库,得到10折交叉验证的乐音识别结果。
3 仿真实验与结果分析
本文采用爱荷华大学电子音乐实验中心(University of IOWA Electronic Music Studio)的音响库[15]作为乐器识别的实验样本库,该样本库录制于不同生产厂家与演奏者的单声部演奏。乐音样本包木管乐器(低音管、长笛)、铜管乐器(萨克斯管、大号)、拨弦乐器(吉他)、击弦乐器(钢琴)、拉弦乐器(小提琴、大提琴)、打击乐器(木琴)共9种乐器。每种乐器选取300个样本,每个样本为采样频率44.1 kHz,16 b单声道数字信号。
3.1 本文模型的评价
为验证本文模型的有效性,使用音色描述符特征+SVM、MFCC+SVM、基于K-SVD字典[16]的正交匹配追踪(Orthogonal Matching Pursuit,OMP)特征+SVM、基于高斯混合模型-隐马尔可夫模型(Gaussian Mixture Model-Hidden Markov Model, GMM-HMM)的概率模型在相同数据库中作横向对比实验。在选取音色描述符特征时使用Relief算法选择7个最佳特征:频谱重心、谐波谱延展、谱偏度、谱峭度、启降奏时间、启降奏能量密度、时域重心。在获取稀疏特征前利用K-SVD算法训练最佳字典,并利用该字典对乐音信号进行OMP分解,匹配追踪7次至残差能量小于0.5%后得到7个匹配系数。GMM-HMM模型使用12维MFCC作为GMM输入,该模型共有9种状态,对应于9种乐器的9种发声结构,通过训练集生成9个模型。
表1显示各模型对同族乐器(管类、弦类)的错分率以及对打击乐器的识别准确率,以此衡量各个模型对共振腔相似乐器识别性能以及对打击乐器的识别性能。
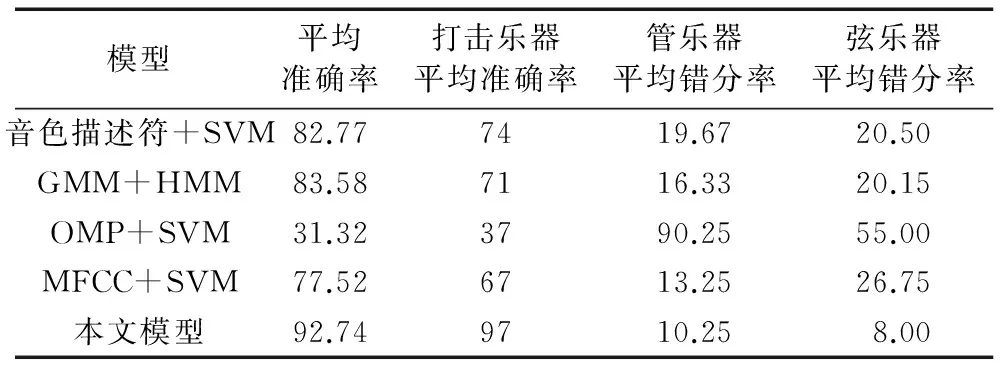
表1 不同模型识别准确率 %Tab. 1 Recognition accuracy of different model %
管乐和弦乐音色差别主要体现在共振体上,它们的音色差异反映了激励源和共振体的不同。MFCC基于激励源-滤波器模型[17]的分析方法容易对管弦乐器错分,尤其弦乐器的平均错分率高达26.75%,吉他、提琴都具有结构相似的共振腔,倒谱特征不利于对其识别。本文模型对打击乐器的识别率比MFCC高30个百分点,这是由于打击乐器频谱平坦,没有明显的共振峰,利用时频特征比倒谱特征更有利于对其识别。GMM-HMM模型以MFCC特征为基础,同样无法避免对打击乐器与结构相似乐器的错分。OMP作为一种贪婪算法,只将乐音信号投射到字典中,却忽略时域信息,而乐器的时域变化对乐器识别起着同样重要的作用。
3.2 MPCA降维的评价
为验证MPCA降维有效性,本文对多尺度时频调制+PCA降维的特征进行纵向对比实验。将时频调制输出展开为向量并同样保留98%方差后利用SVM降维。MPCA方式识别准确率为92.74%,PCA则为86.31%,两种降维方式对9种乐器的识别结果混淆图如图3所示。MPCA降维方式比PCA降维方式的平均提高识别准确率6.43%。
特征降维的本质是将高维数据投影到低维空间,投影方式决定数据可分度,最终影响分类器识别的准确率。实验结果验证了PCA降维破坏原始数据固有的高阶结构和内在相关性,不利于对张量特征的处理,MPCA相比PCA能够将数据投射到更易分的低维空间。
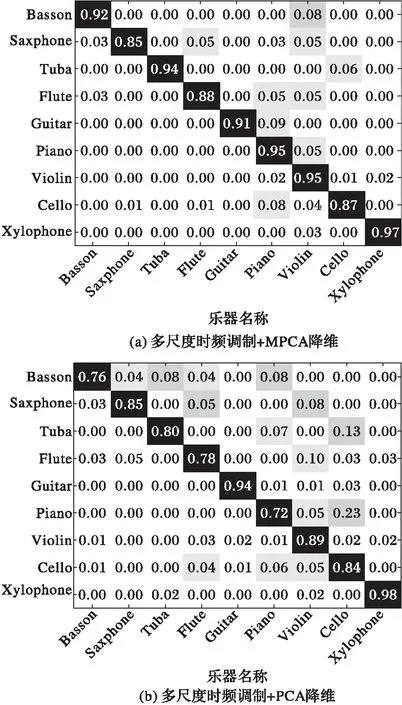
图3 MPCA降维与PCA降维混淆图 Fig. 3 Confusion graph of MPCA and PCA
4 结语
乐器的发音机理各有差异,管弦乐器具有明显共振结构且同类乐器结构相似,打击乐器无明显共振峰。此外,谐波具有重要作用,而倒谱处理忽略了谐波信息,所以倒谱特征并不能反映乐音的听觉特性。音色描述符对频谱或包络进行定量描述,这些特征的选取会随着乐库的改变而改变。稀疏表示将信号投影至字典,并不能表征乐音波形的时域信息。概率特征对乐音的种类与启奏时刻有前提假设。考虑到音色定义为使人在听觉上区分不同乐器的属性,基于人耳听觉特性的特征必然更有利于音色的识别。本文利用多尺度时频调制对乐音进行特征提取从而提取乐音的时频信息,基于多尺度时频调制特征对打击乐器的与结构相似的乐器识别率比音色描述符特征、倒谱特征、稀疏特征、概率特征更高。
本文研究表明基于MFCC的识别模型更适合针对共振腔更加明显的乐器进行识别,比如弦乐器和管乐器,但对结构相似的乐器错分率较高,对于共振不明显的打击乐器识别准确率较低。基于多尺度时频调制的特征描述了乐音频率成分随时间的变化信息,类似于听觉感受,它并不依赖乐器的机理构造,它描述的是乐器频率成分变化的特点,不同的乐器拥有不同频率变化方式,所以对打击乐器与结构相似的乐器识别比其他特征更加准确。对于张量数据的降维处理,传统PCA方式破坏数据内在相关性使得数据可分性变差,MPCA能够将数据投影到易分的低维空间。
本文中乐器的识别的样本是高信噪比且无混响的单声部音符,样本均录制于录音棚的理想环境,在存在噪声以及混响的实际环境进行乐器识别以及对多声部音乐信号进行识别是今后进一步研究的内容。
参考文献(References)
[1] STURM B L. The state of the art ten years after a state of the art: future research in music information retrieval [J]. Journal of New Music Research, 2014, 43(2): 147-172.
[2] BHALKE D G, RAO C B R, BORMANE D S. Automatic musical instrument classification using fractional Fourier transform based-MFCC features and counter propagation neural network [J]. Journal of Intelligent Information Systems, 2016, 46(3): 425-446.
[3] LOUGHRAN R, WALKER J, O’NEILL M, et al. Musical instrument identification using principal component analysis and multi-layered perceptrons [C]// ICALIP 2008: Proceedings of the 2008 International Conference on Audio, Language and Image Processing. Piscataway, NJ: IEEE, 2008: 643-648.
[4] BURRED J J, ROBEL A, SIKORA T. Dynamic spectral envelope modeling for timbre analysis of musical instrument sounds [J]. IEEE Transactions on Audio Speech & Language Processing, 2010, 18(3): 663-674.
[5] YU L F, SU L, YANG Y H. Sparse cepstral codes and power scale for instrument identification [C]// ICASSP 2014: Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ: IEEE, 2014: 7460-7464.
[6] HAN Y, LEE S, NAM J, et al. Sparse feature learning for instrument identification: effects of sampling and pooling methods [J]. Journal of the Acoustical Society of America, 2016, 139(5): 2290-2298.
[7] HU Y, LIU G. Instrument identification and pitch estimation in multi-timbre polyphonic musical signals based on probabilistic mixture model decomposition [J]. Journal of Intelligent Information Systems, 2013, 40(1): 141-158.
[8] WEESE J L. A convolutive model for polyphonic instrument identification and pitch detection using combined classification [J]. Machine Learning, 2013, 15(2): 12-17.
[9] ARORA V, BEHERA L. Instrument identification using PLCA over stretched manifolds [C]// NCC 2014: Proceedings of the 2014 20th National Conference on Communications. Piscataway, NJ: IEEE, 2014: 1-5.
[10] PATIL K, PRESSNITZER D, SHAMMA S, et al. Music in our ears: the biological bases of musical timbre perception [J]. PLOS Computational Biology, 2012, 8(11): e1002759.
[11] BINER L, SCHAFER R. Theory and Applications of Digital Speech Processing [M]. Upper Saddle River, NJ: Prentice Hall Press, 2011: 124-136.
[12] MEDDIS R, LOPEZPOVEDA E, FAY R R, et al. Computational Models of the Auditory System [M]. Berlin: Springer, 2010: 135-149.
[13] ABDI H, WILLIAMS L J. Principal component analysis [J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433-459.
[14] LU H, PLATANIOTIS K N, VENETSANOPOULOS A N. MPCA: multilinear principal component analysis of tensor objects [J]. IEEE Transactions on Neural Networks, 2008, 19(1): 1-18.
[15] University of IOWA Electronic Music Studio. A musical instrument database [DB/OL]. [2017- 03- 08]. http://theremin.music.uiowa.edu/MISflute.html.
[16] JIANG Z, LIN Z, DAVIS L S. Label consistent K-SVD: learning a discriminative dictionary for recognition [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(11): 2651-2664.
[17] 韩纪庆,张磊,郑铁然.语音信号处理[M].北京:清华大学出版社,2004:76-85.(HAN J Q, ZHANG L, ZHENG T R. Voice Signal Processing [M]. Beijing: Tsinghua University Press, 2004: 76-85.)
WANGFei, born in 1991, M. S. candidate. His research interests include audio signal processing, deep learning.
YUFengqing, born in 1962, Ph. D., professor. Her research interests include audio signal processing, time-frequency analysis of non-stationary signals.

