基于提升静态小波变换与联合结构组稀疏表示的多聚焦图像融合
邹佳彬,孙 伟
(中国矿业大学 信息与控制工程学院,江苏 徐州 221008)
0 引言
光学传感器通常无法获取同一场景内不同景深的多个目标都清晰的图像,常用的解决方法是借助多个传感器一次成像或单个传感器多次成像得到聚焦在不同区域的多幅图像[1]。多幅图像之间往往存在着大量的冗余信息,不利于图像的分析与处理,因此,多聚焦图像融合方法得到了广泛的研究,它将不同景深的多幅图像进行融合,降低图像间信息的冗余度,得到便于后续处理的清晰图像。目前,应用于多聚焦图像融合的算法很多。基于多尺度分析的图像融合技术,模拟了人类视觉系统由“粗”及“细”感知物体的方式,可以得到较好的融合结果,所以基于多尺度分析的图像融合技术一直成为图像融合领域的研究热点。图像经多尺度变换分解后,能够针对多方向、多尺度层采取不同融合策略,突出重要的细节特征信息,获得更好的融合效果。小波变换作为一种图像多尺度分解的工具,因具有良好的时域和频域局部特性以及多分辨率特性,而在图像融合领域中得到了广泛应用[2]。随着小波变换相关理论的不断成熟,传统小波变换的缺陷如平移变性和较少的方向选择性等随之展现出来。于是Sweldens等[3]致力于研究具有更高性能的多尺度变换工具,提出了第二代提升小波变换,主要是关于张量积小波的提升方式。然而,传统提升小波变换仍具有部分缺点如不具有平移不变性,在融合图像时容易产生伪吉布斯现象[4],使融合图像失真严重。因此本文采用文献[5]提出的提升静态小波变换(Lifting Stationary Wavelet Transform, LSWT)作为多尺度变换工具,克服了传统小波变换的平移变性等缺陷,得到具有平移不变性的多尺度变换图像。
基于多尺度变换的图像融合算法中,融合规则的选择和设计决定了融合图像质量,因为图像经多尺度变换可分解为低频部分和高频部分,而图像的高频部分由于分解层数的不同而存在着不同的尺度,针对高低频子带各自的物理特征,分别设计高频子带和低频子带的融合规则。通常情况下,低频子带包含了源图像的主要能量,可以看成是源图像的近似信息,系数的选择大多采用直接平均法,该方法虽然简单,但在一定程度上降低了图像的对比度,以及未考虑到人眼的视觉特征,从而使源图像中的部分有用信息丢失;高频子带包含图像的边缘、轮廓等大多数细节信息,通常系数的选择方案直接作用于高频子带系数,没有考虑到局部区域里像素间的相关性,纹理细节得不到较好的保留。
近些年来,由于稀疏表示模型可以高效地提取源图像的潜在信息,基于稀疏表示的图像融合方法得到了十分广泛的研究及应用。文献[6]将基于稀疏表示的融合方法直接应用于灰度图像,并研究了过完备字典对图像融合质量的影响;文献[7]将稀疏模型与多尺度变换相结合,较好地解决了稀疏表示模型对图像高频子带系数不能完好逼近的问题;文献[8]提出了结合非下采样轮廓波变换(Non-Subsampled Contourlet Transform, NSCT)与稀疏表示的多聚焦图像融合方法,一定程度上克服了传统稀疏表示方法容易造成图像边缘、纹理等细节趋于平滑的缺陷。随着稀疏表示的深入研究,联合稀疏表示(Joint Sparse Representation, JSR)模型被Baron等[9]提出,文献[9]展现了三种联合稀疏模型(Joint Sparsity Model, JSM)来描述信号之间的相关性,分别为JSM1、JSM2与JSM3。模型指出: 所有信号之间具有相关性,即具有相同的公共稀疏部分与各信号独有的稀疏部分。肖新耀等[10]提出一种基于àtrous小波和联合稀疏表示的遥感图像融合方法;Li等[11]提出了联合稀疏表示的多聚焦图像融合方法;宗静静等[12]提出了联合稀疏表示的医学图像融合及同步去噪算法。上述基于联合稀疏表示模型的融合算法充分地利用图像间的相关性,所得融合图像的亮度、对比度较高,图像纹理细节相对清晰,源图像清晰部分特征得到较好的保留,但融合图像中仍存在一定的块状效应影响。
通常稀疏表示模型是将原始图像先分块,然后将图像块按列向量形式排列成矩阵,利用过完备字典进行稀疏求解;然而当基于块的稀疏表示模型中采用图像块作为基本单元时,每个图像块在字典学习与稀疏编码的过程中相互独立,忽略了相似块间的联系,往往得到的稀疏系数不够准确,同时字典训练中计算复杂度较高。针对这种情况,Zhang等[13]指出根据图像本身具有的非局部相似性,即相似图像块的像素值与结构大致相同,采用相似性结构组为基本单元,对结构组进行稀疏表示可以得到较好的处理结果。研究表明结构组稀疏表示比传统的基于图像块的稀疏表示模型计算速度快,块状效应减少,同时图像重构以及降噪方面效果更加显著。近年来,图像的非局部相似性在压缩感知以及图像融合方面得到了广泛的应用。李祥灿[14]利用结构组稀疏表示研究了自然图像超分辨率重建算法;张晓等[15]提出基于结构组稀疏表示的遥感图像融合算法,将表征图像结构相似性的结构组概念应用到稀疏表示的图像融合算法中,将结构组作为字典与稀疏求解的基本单位,在结构组内采用奇异值分解方法学习组稀疏系数,采用通用分量替换融合框架进行图像融合,取得了较好的融合效果。
综上所述,利用多尺度变换在图像融合中的优势,本文选择提升静态小波变换(LSWT)作为多尺度变换工具,针对LSWT分解得到的高低频子带的各自特征选择不同的融合方案。融合图像低频子带系数时,由于低频子带稀疏性较差,传统基于图像块的稀疏表示模型在图像融合中容易产生块效应影响,字典建立复杂度高,因此,根据图像本身具有的非局部相似性,选择结构组作为字典和稀疏求解基本单位;同时考虑到联合稀疏表示模型能够充分利用低频子带图像之间的关联性并可用较少的系数精确表示图像特征,本文用结构组代替联合稀疏表示中的图像块作为字典和稀疏求解基本单位,得到联合结构组稀疏表示模型来指导融合,提高计算速度,增强降噪效果,降低块效应影响,使清晰部分得到更好的保留。LSWT分解得到的高频子带稀疏性较好,并且能够体现图像不同方向、不同角度的纹理等细节特征,因此低频子带融合规则不适用于高频子带。高频子带图像可看成是由许多的像素点构成,仅凭单个像素点不能清楚地表示出图像纹理等细节,需要区域内的像素点共同体现,又考虑到拉普拉斯能量和在融合高频系数时表现出的高效性,能包含大部分的细节信息,因此,采用方向区域拉普拉斯能量和与匹配度相结合的自适应融合算法指导融合。本文算法流程如图1所示。
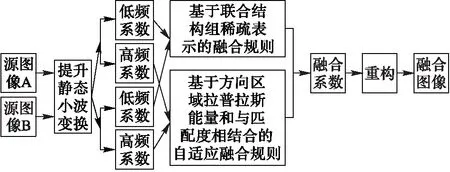
图1 本文算法流程 Fig. 1 Flow chart of the proposed algorithm
1 提升静态小波变换
为克服传统小波变换以及第二代提升小波变换存在的不足,本文采用LSWT作为多尺度变换工具。通过在传统提升小波变换的基础上取消奇偶分裂环节并在相应滤波器系数间插入一定个数的零来实现滤波器的延拓,便能得到具有平移不变性的提升静态小波变换[4]。其分解与重构过程如图2所示。
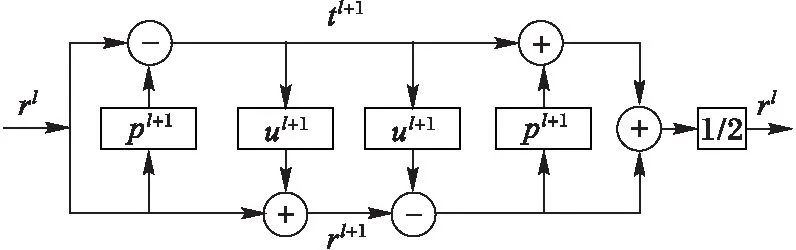
图2 提升静态小波分解与重构图 Fig. 2 LSWT decomposition and recomposition diagram
图2中:rl+1与tl+1分别为输入信号rl经LSWT第l+1层分解得到的低频与高频子带系数;pl+1与ul+1为LSWT的预测与更新滤波器系数,表示如下:
(1)
(2)
其中:pi(i=0,1,…,I-1)与uj(j=0,1,…,J-1)分别为原提升小波变换的预测与更新滤波器系数;I、J分别为原预测算子p和更新算子u的系数个数。
2 联合结构组稀疏表示
2.1 结构组的构建
稀疏表示以压缩传感理论为基础。稀疏表示的基本模型是用字典中少量原子的线性组合来描述信号,即大部分原子的系数绝对值都为零,只有少数原子的系数非零,图像信息越稀疏,稀疏表示就越准确[10]。传统基于图像块的稀疏表示模型通常对不同的图像块分别进行稀疏表示,例如传统图像编码中采用的分块离散余弦变换,然而字典训练与稀疏优化求解的过程比较复杂,计算量大以及耗时长。近年来,图像的结构稀疏性或组稀疏性得到了广泛的应用。
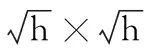
为了提高图像处理的运行效率,通常需要对图像的每一个结构组进行最佳稀疏表示,得到自适应于每一个结构组Vyk的最佳稀疏表示字典Dyk。
2.2 联合稀疏表示
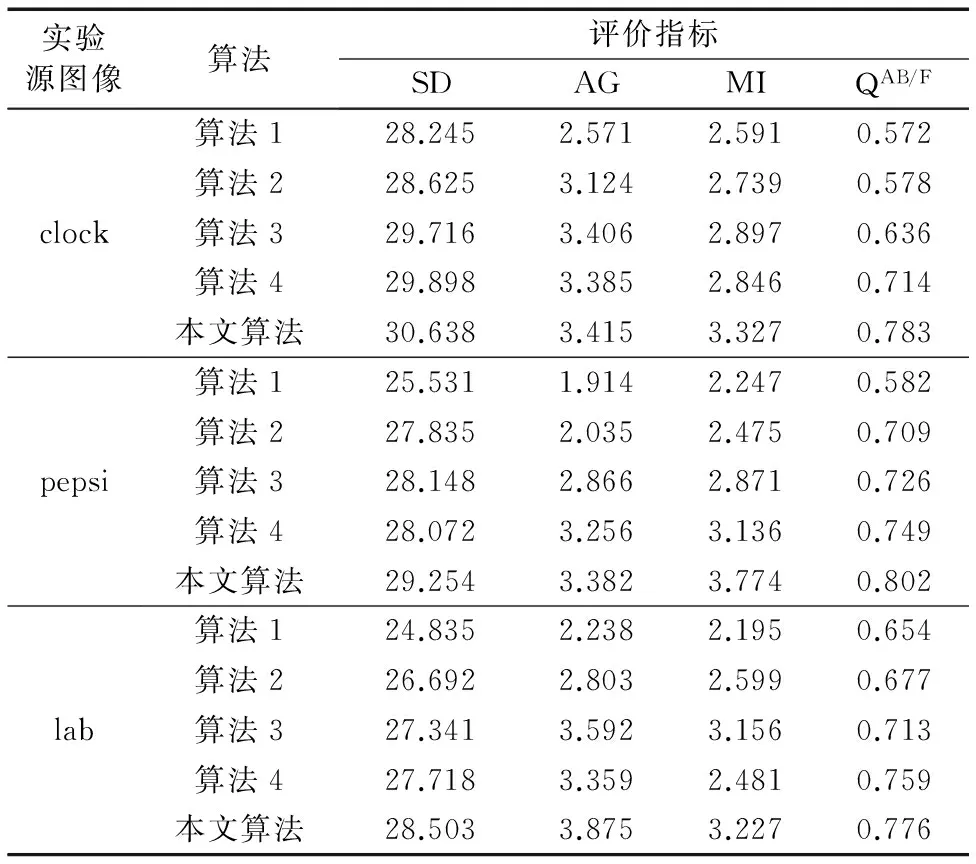
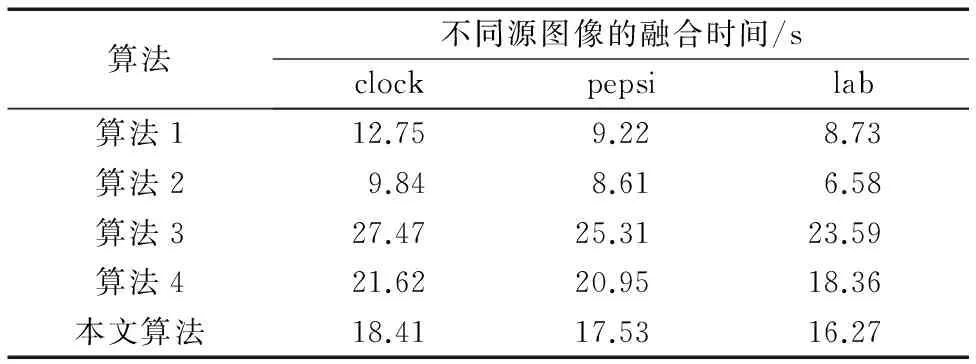
分布式压缩感知(Distributed Compressed Sensing, DCS)由Baron等[9]于2009年提出,联合稀疏表示模型来源于分布式压缩感知理论,是其核心内容。Baron等[9]提出了3种不同的联合稀疏表示模型,在联合稀疏表示模型JSM1中,Z={z1,z2,…,zF}表示F信号所组成的信号集合,其中zi∈Rn,假设给定的过完备字典为D∈Rn×m(n zi=Dac+Dai+ni;i=1,2,…,n (3) 其中:ac∈Rm与ai∈Rm分别为所有信号的公共稀疏系数和各自的独立稀疏系数,Dac和Dai分别表示所有信号的公共信息部分和各自的独立信息部分,ni表示信号噪声。 信号整体的联合稀疏表示(JSR)如式(4)所示: Z=DJSRA+n (4) 结合稀疏表示理论,稀疏系数A可以通过求解下面的优化问题得到,即: (5) 优化问题式(5)是个无确定解析式的困难问题(Non-determined Polynomial hard, NP-hard)[16],无法直接求解,很多逼近算法能够有效地逼近最优解。考虑到正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法的快速特点,文献[17]提出了正则的OMP——正则化正交匹配追踪(Regularized Orthogonal Matching Pursuit, ROMP)稀疏分解算法,ROMP稀疏分解算法属于贪婪系列,可较好地克服基追踪(Basis Pursuit, BP)的高复杂度与OMP的低精度问题。 假设X={x1,x2} 表示2幅图像所组成的信号集合,x1,2∈RM×N,结构组联合稀疏表示框架表示如下: 3)联合结构组矩阵Vxk中信号整体的联合稀疏如下所示: Vxk=DxkJSRAxk+nxk (6) 结合稀疏表示理论,稀疏系数Axk可以通过求解下面的优化问题得到,即: (7) 4)采用ROMP稀疏分解算法求解上述优化问题,可得每个联合结构组矩阵Vxk的稀疏系数Axk。 LSWT得到的低频子帯是图像的近似描述,包含图像的主要能量,但低频子带稀疏性较差。针对低频子带稀疏性较差这一缺点,考虑到联合稀疏表示模型能够充分利用低频子带图像之间的关联性以及结构组可以有效地表征图像本身具有的非局部相似性,本文选择联合结构组稀疏表示模型来指导低频子带系数融合。低频系数融合方法总体框架如下: 1)图像LSWT分解。将两幅源图像进行LSWT分解(本文采用2层分解),得到低频子带系数I1与I2。 (8) 5)重构。根据VFxk=DxkaFxk重构得到融合图像第k个结构组矩阵VFxk,利用式(9)将每一个结构组放回到重建图像的对应位置,并将全部结构组进行取均值处理,最终得到低频子带融合图像I,其中./表示两个向量之间对应元素进行除法的算子。 (9) 源图像经LSWT分解后的高频子带中,高频系数表示图像细节的变化情况,直接地反映图像的边缘与纹理等细节信息分布情况。高频系数值越大,代表着边缘与纹理特征更加明显,需要被更好地保留。考虑到人类视觉系统特性,人眼对单个像素的灰度取值并不敏感,图像清晰与否是由区域内像素共同体现[18],因此,本文采用了基于区域特征的融合规则。已知拉普拉斯能量和(Sum Modified-Laplacian, SML)能较好地反映图像的边缘化程度,可恰当地描述图像的灰度变化信息,进而反映空间细节,增强图像可分辨性,相对于图像的空间频率、方差、以及图像的区域能量等,SML 在融合图像时处理高频子带系数表现出明显的优越性[19],同时考虑到高频系数呈现明显的方向特性,因此将方向区域拉普拉斯能量和作为区域特征用于图像融合中。 如果用fd,l(x,y)表示源图像位于(x,y)处d(d为LSWT分解得到3个方向)方向,l(l=1,2,…,L)尺度高频子带细节系数,则待融合图像高频子带各元素的拉普拉斯算子MLd,l以及方向区域拉普拉斯算子能量和(DRSMLd,l)表示如下: MLd,l(x,y)=|2fd,l(x,y)-fd,l(x-step,y)- fd,l(x+step,y)|+|2fd,l(x,y)-fd,l(x,y-step)- fd,l(x,y+step)| (10) (11) 两幅图像A与B的高频子带中对应元素的相关方向区域拉普拉斯能量和为: (12) 其中:step表示系数间的可变距离,本文取step=1;Wd为窗口函数;a×b为窗口大小(例如3×3、5×5或7×7)。经LSWT分解后的各高频子带系数的分布呈现出明显的方向特征,分别表现为水平、垂直和对角方向,如果选用统一的窗口函数,则突显不出区域的方向特性。据此可以对高频子带选取各自相关性较强的方向区域,而不使用统一区域模板,增强区域方向相关性[20]。考虑到高频子带系数变化比较剧烈,窗函数在处理邻域像素时应能够突出中心像素的作用,因而本文选取中心数值较大、周围数值较小的窗函数。综上所述,本文方向区域窗口模板Wd(a,b)如图3所示,利用不同方向区域窗口模板生成各个高频子带的方向区域拉普拉斯能量和。 图3 方向区域窗口模板 Fig. 3 Window template of directional region 计算两幅图像A,B中高频子带系数的区域匹配度为: (13) Td,lA,B反映了两幅图像位置(x,y)处d方向,l尺度高频子带区域能量的近似程度。当A、B比较接近时,Td,lA,B趋向于1;而当A、B差别很大时,Td,lA,B趋向0。本文加权融合规如下: fd,lZ(x,y)=ωA(x,y)fd,lA(x,y)+ωB(x,y)fd,lB(x,y) (14) ωB(x,y)=1-ωA(x,y);ωA(x,y)= (15) 考虑到式中Td,lA,B为与T有关的阈值,定义自适应阈值T如下: T=0.5*(max(Td,lA,B)+min(Td,lA,B)) (16) 当Td,lA,B≥T,表明两幅图像A、B差别较小,相关程度高,因此根据方向区域拉普拉斯能量和大小确定自适应因子进行图像加权融合;当Td,lA,B 本文选取多聚焦图像clock、pepsi、lab作为实验对象。图4(a)与图4(b)分别是已配准的左聚焦clock图像与右聚焦clock图像,已配准的左聚焦pepsi图像与右聚焦pepsi图像,图4(c)为存在配准误差的左聚焦lab图像与右聚焦lab图像(学生头部存在配准误差)。实验中采用LSWT对图像进行分解与重构,分解层数为2,区域模板大小为3×3,实验源图像如图4所示。所有实验都是在Matlab R2008a平台上进行,硬件条件为英特尔双核CPU、频率3 GHz、内存2 GB。 图4 实验选用的多聚焦源图像 Fig. 4 Multi-focus source images for experiment 为验证本文改进算法的有效性,本文与其他4种算法进行实验对比。算法1和算法2采用基于小波变换与提升静态小波变换作为多尺度变换工具,低频系数加权平均、高频系数模值取大的融合算法,算法3采用文献[7]提出的基于多尺度变换和稀疏表示的图像融合方案;算法4采用文献[10]提出的基于联合稀疏表示的图像融合方案,算法5采用本文所提出的融合方案,比较5种算法以此来验证本文融合算法的优越性。图5(a)~(e)为5种算法融合clock、pepsi、lab多聚焦源图像的融合图像;图6(a)~(e)为图5(a)~(e)融合图像的局部细节放大图;为更好地比较5种融合方法的融合效果,本文给出图5中融合图像与图4相应右聚焦源图像之间的残差结果,图7(a)~(e)为图5中clock、pepsi、lab的融合图像与图4(a)~(e)右聚焦源图像的相应残差图。 图5 采用不同融合算法得到的融合图像 Fig. 5 Fusion image obtained by different fusion algorithms 图6 图5的细节图 Fig. 6 Details of Fig.5 图7 图4右聚焦源图像与图5的相应残差图 Fig. 7 Difference images of Fig.5 and the right multi-focus source image of Fig.4 通过客观评价指标,可以定量地比较不同融合图像的质量。本文选取4个客观评价指标分别为:标准差(Standard Deviation, SD)、平均梯度(Average Gradient, AG)、互信息量(Mutual Information, MI)、边缘信息保持度(QAB/F)。标准差表征了图像像素分布程度,决定图像对比度的高低;平均梯度指图像的边界或影线两侧附近灰度的明显差异程度,可用来表示图像清晰度;互信息用于衡量融合图像包含源图像信息量的大小;边缘信息保持度表征源图像中的边缘细节信息注入到融合图像的转移量。一般情况下,4个客观评价指标越大,表示融合图像质量越高,图像越清晰。表1为图5中clock、pepsi、lab融合图像相应的客观评价指标。 表1 clock、pepsi、lab的图像客观评价指标Tab. 1 Image objective evaluation index of clock,pepsi,lab 从图5(a)、(b)融合图像以及图6(a)、(b)的细节图像中可以看出,图5(a)clock的大闹钟边缘与pepsi的上方英文字母边缘处出现波纹与虚假信息,存在伪影现象,图像清晰度较差,针对存在配准误差的lab多聚焦图像,图5(a)lab的实验人员头部出现更为严重的伪影现象。图5(b)clock的大闹钟边缘、pepsi的上方英文字母边缘以及lab的学生头部边缘处则此类现象得到缓解,边缘较为清晰。其主要原因是采用传统小波变换对图像进行分解和重构时需要进行采样操作,使得传统的小波变换不具有平移不变性,导致了融合图像失真,边缘存在伪影现象,使融合图像的视觉效果较差。特别是对存在配准误差的lab多聚焦图像进行融合时,由于源图像之间存在一定位移,没有移不变功能的方法得到融合图像在边缘附近的伪吉布斯现象更为明显。而LSWT对图像进行分解与重构时因取消了奇偶分裂环节没有对图像进行上下采样操作,具有平移不变性,因此能较好地克服伪吉布斯现象并提高融合图像质量。根据残差图对比结果,能更直观地看出上述2种方法的差异,图7(b)clock、pepsi、lab图像相比7(a)中图像残差较少,说明基于LSWT的融合算法在融合性能方面优于基于传统小波变换的融合算法。为了更客观地评价两种融合算法在多聚焦图像融合中的性能,采用4个客观评价指标进行定量比较,对比结果如表1所示,从中可以看出提升静态小波变换方法可以消除由于传统小波变换不具有平移不变性所产生的伪吉布斯现象,边缘特征显著提高,融合效果相对更好。 从图5(b)~(e)以及局部细节图6(b)~(e)的对比中可以看出,图5(b)融合图像相比图5(c)~(e)的视觉效果较差,这是因为方法2中低频系数取平均规则所获得的融合图像并不能有效提取源图像信息并注入到融合图像中,以及高频系数模值取大规则直接作用于高频子带系数,没有考虑到局部区域里像素间的方向性与相关性,融合图像的纹理细节得不到较好的保留。图5(c)clock的大闹钟与pepsi的上方英文字母边缘比较模糊,存在一定的块状效应,图5(c)lab的学生头部也存在此类现象,这是因为方法3采用基于稀疏表示的融合方法平滑了图像的细节引起的。图5(d)融合图像在对比度方面相对于5(c)融合图像相差不大,但虚影相对减少,纹理细节更清晰,主要是因为方法4中联合稀疏表示模型充分利用图像之间相关性,使得源图像清晰特征得到了较好的保留。本文方法所得融合结果图5(e)边缘、纹理等细节更为清晰,对比度更高,图像视觉效果最好,主要是因为本文采用结构组代替图像块作为联合稀疏表示模型中的基本单元,消除了图像的块状效应影响,增强了图像的自相似性,因而可以得到视觉效果更好的融合图像。根据图7中的残差结果进一步比较4种方法的融合性能,从中可以直观地看到,方法2所得残差图的残差像素最多,融合效果最差,方法3与方法4所得残差图效果有所提高,但仍存在一定的残差像素,不能将源图像清晰像素较好地转移到融合图像中,本文算法所得残差图的残差像素在清晰区域几乎为0,表明本文方法最为有效地融合了源图像清晰像素,所得融合图像效果最好。根据表1中4个客观评价指标对融合图像进行定量分析比较,本文算法评价指标最优,特别是互信息(MI)和边缘信息保持度(QAB/F)指标,从客观的角度验证了本文算法得到的融合图像在对比度、清晰度以及边缘细节信息的保留等方面优于其他几种算法。因此综合来看,本文算法所得融合图像性能最优越,最接近标准图像。 表2为5种图像融合算法处理clock、pepsi、lab源图像的运行时间对比。从表2中可以看出:本文算法相对于算法3与算法4,所用时间较少,因为本文算法采用结构组代替传统稀疏表示中的图像块作为字典和稀疏求解基本单位,显著降低字典学习的计算复杂度,同时优化了稀疏求解过程,因而运行时间较少;但相比算法1与算法2,运行时间较高,因为算法1和2均采用低频系数加权平均、高频系数模值取大的融合规则,对于低频子带细节系数,平均法虽然简单,但在一定程度上降低了图像的对比度,使源图像中的部分有用信息丢失;对于高频子带细节系数,没有考虑区域特征,直接作用于高频子带细节系数,融合图像质量下降。综合上述实验分析,本文算法在保证融合图像质量的情况下,运行时间相对较少。 表2 各种融合算法的运行时间对比Tab. 2 Running time comparison of a variety of fusion algorithm 本文针对多聚焦图像融合提出了基于LSWT与联合结构组稀疏表示的多聚焦图像融合算法。采用的提升静态小波变换克服了传统的小波变换由于不具有平移不变性所导致的在图像融合时边缘处产生的“伪吉布斯”现象,在一定程度上抑制了图像的失真现象。在提升静态小波变换基础上,本文提出的融合规则为:低频系数采用基于联合结构组稀疏表示的融合算法,高频系数采用方向区域拉普拉斯能量和与匹配度相结合的自适应融合算法。实验结果表明本文算法运行时间相对较少,并可以充分提取源图像清晰部分信息并注入到融合图像中,图像边缘、轮廓细节得到较好的保留,融合图像效果更佳。下一步研究工作可以在本文方法的基础上对彩色图像进行多聚焦融合理论分析,实现彩色图像的实时融合。 参考文献(References) [1] 杨勇,万伟国,黄淑英,等.稀疏表示和非下采样shearlet变换相结合的多聚焦图像融合[J].小型微型计算机系统,2017,38(2):386-392.(YANG Y, WAN W G, HUANG S Y,et al. Spare representation and non-subsampled shearlet transform for multi-focus image fusion[J]. Journal of Chinese Computer Systems, 2017, 38(2): 386-392.) [2] 周挺,胡斌.基于小波变换的自适应多聚焦图像融合算法[J].传感技术学报,2010,23(9):1272-1276.(ZHOU T, HU B. Adaptive algorithm of multi-focused image fusion based on wavelet transform[J]. Chinese Journal of Sensors and Actuators, 2010, 23(9): 1272-1276.) [3] SWELDENS W. The lifting scheme: a construction of second generation wavelets [J]. SIAM Journal on Mathematical Analysis, 1998, 29(2): 511-546. [4] 易正俊,李华锋,宋瑞晶.改进提升小波变换的空间频率比图像融合[J].光电工程,2009,36(7):65-70.(YI Z J, LI H F, SONG R J. Spatial frequency ratio image fusion method based on improved lifting wavelet transform [J].Opto-Electronic Engineering, 2009, 36(7): 65-70.) [5] LEE C S, LEE C K, YOO K Y. New lifting based structure for undecimated wavelet transform [J]. Electronics Letters, 2000, 36(22): 1894-1895. [6] ANG B, LI S. Pixel-level image fusion with simultaneous orthogonal matching pursuit [J]. Information Fusion, 2012,13(1): 10-19. [7] LIU Y, LIU S, WANG Z. A general framework for image fusion based on multi-scale transform and sparse representation [J]. Information Fusion, 2015, 24(1): 147-164. [8] 欧阳宁,郑雪英,袁华.基于NSCT和稀疏表示的多聚焦图像融合[J].计算机工程与设计,2017,38(1):177-182. (OUYANG N, ZHENG X Y, YUAN H. Multi-focus image fusion based on NSCT and sparse representation [J]. Computer Engineering and Design, 2017, 38(1): 177-182.) [9] BARON D, DUARTE M F, WAKIN M B, et al. Distributed compressive sensing [C]// ICASSP 2009: Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ: IEEE, 2009: 2886-2889. [10] 肖新耀,许宁,尤红建.一种基于àtrous小波和联合稀疏表示的遥感图像融合方法[J].遥感技术与应用,2015,30(5):1021-1026.(XIAO X Y, XU N, YOU H J. A method on remote sensing image fusion based on àtrous wavelet transform and joint sparse representation [J]. Remote Sensing Technology and Application, 2015,30(5): 1021-1026.) [11] LI X, LI X, ZHAO H, et al. Fusing images using joint sparse representation [J]. ICIC Express Letters, 2014, 8(12): 1377-1379. [12] 宗静静,邱天爽,郭冬梅.联合稀疏表示的医学图像融合PHNT及同步去噪[J].中国生物医学工程学报,2016,35(2):133-140.(ZONG J J, QIU T S, GUO D M. Simultaneous medical image fusion and de-noising with joint sparse representation [J]. Chinese Journal of Biomedical Engineering, 2016, 35(2): 133-140.) [13] ZHANG J, ZHOU D, GAO W. Group-based sparse representation for image restoration [J]. IEEE Transactions on Image Processing, 2014, 23(8): 3336-3351. [14] 李祥灿.基于组稀疏表示的自然图像超分辨率算法研究[D].南京:南京理工大学,2014:28-35.(LI X C. Natural image super-resolution method research based on group sparse representation[D]. Nanjing: Nanjing University of Science and Technology, 2014:28-35.) [15] 张晓,薛月菊,涂淑琴,等.基于结构组稀疏表示的遥感图像融合[J].中国图象图形学报,2016,21(8):1106-1118. (ZHANG X, XUE Y J, TU S Q, et al. Remote sensing image fusion based on structural group sparse representation [J]. Journal of Image and Graphics, 2016, 21(8): 1106-1118.) [16] NATARAJAN B K. Sparse approximate solutions to linear systems [J]. SIAM Journal on Computing, 1995, 24(2): 227-234. [17] DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit [J]. IEEE Transactions on Information Theory, 2012, 58(2): 1094-1121. [18] 刘贵喜,杨万海.基于小波分解的图像融合算法及性能评价[J].自动化学报,2002,28(6):927-934.(LIU G X, YANG W H. A wavelet-decomposition-based image fusion scheme and its performance evaluation [J]. Acta Automatica Sinica, 2002, 28(6): 927-934.) [19] 董红霞,易正俊,叶晓斌.提升静态小波特征对比度多聚焦图像融合算法[J].计算机应用研究,2012,29(2):56-61.(DONG H X, YI Z J, YE X B. Multi-focus image fusion scheme based on features contrast of lifting stationary wavelet [J]. Application Research of Computers, 2012, 29(2): 56-61.) [20] 朱辉,江卓斌,胡斌杰.一种改进的基于方向区域能量的多聚焦图像融合算法[J].传感器与微系统,2011,30(9):131-138.(ZHU H, JIANG Z B, HU B J. An improved algorithm of multi-focused image fusion based on directional region-energy [J]. Transducer and Microsystem Technologies, 2011, 30(9): 131-138.) This work is partially supported by the Primary Research & Development Plan of Shandong Province (2015GSF120009). ZOUJiabin, born in 1992, M. S. candidate. His research interests include image processing, pattern recognition. SUNWei, born in 1963, Ph. D., professor. His research interests include monitoring, optimization and advanced control of process and system, computer vision, machine learning.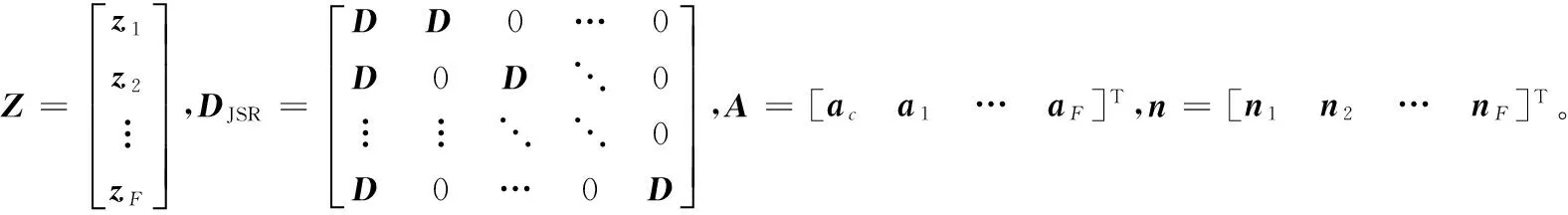
2.3 联合结构组稀疏表示框架
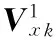
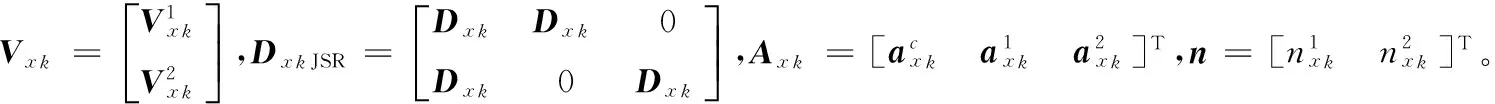
3 基于LSWT的多聚焦图像融合框架
3.1 低频子带系数融合算法
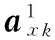
3.2 高频子带系数融合算法
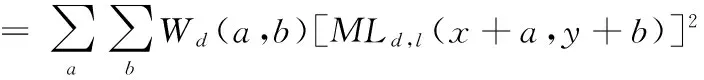
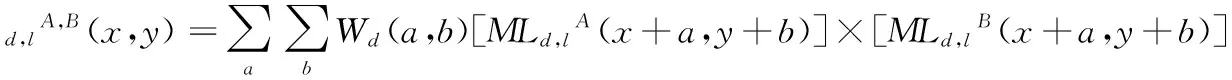
4 实验结果分析




5 结语

