抑制孤立簇的软件模块化优化算法
牟立峰,王方媛
(上海大学 悉尼工商学院,上海 201899)
0 引言
在软件产品设计和开发过程中,广泛应用模块化方法来提高软件产品架构的质量。但随着软件产品的不断进化,软件产品趋向大型化和复杂化,仅依靠专家经验无法应对复杂的模块化方案设计问题。因此,如何运用智能算法自动生成大型复杂软件系统的高质量模块划分备选方案对软件产品的设计过程中的关键决策有着重要意义,与其相关的研究工作也成为学术界关注的热点[1]。
软件模块化目的是得到模块化较好的聚类目标,模块化优化问题主要包括设计模块化质量的量化指标[2-7]和更强寻优能力的算法[6-15]。
在量化指标方面,研究工作主要从软件产品的属性上着手量化软件架构质量,其中最重要的两个属性是内聚和耦合。内聚指的是在同一个子系统中模块之间的联系,耦合指的是不同的子系统中模块的联系[2]。很多学者基于内聚和耦合的关系提出了衡量软件模块划分方案优劣的指标。Stevens等[3]在1974年首先提出用高内聚和低耦合指标来衡量软件模块化的质量,并提出了一个内聚和耦合的七分制的衡量方法,为之后软件质量指标提供了方法和思路。针对面向对象的软件产品,学术界也提出了其他指标,包括:属性隐藏因素指标(Attribute Hidden Factor, AHF)和方法隐藏因素指标(Method Hidden Factor, MHF),这些指标能更好地测量封装的程度[4]。之后Tucker等[5]提出了指标EVM(EValuation Metric),该指标之前应用于时间序列分析,并且具有优秀的鲁棒性。随后研究工作的深入,学者发现:一味地追求高内聚和低耦合并不可取;高质量的软件架构普遍拥有内聚和耦合相对平衡的模块化特性[2]。基于该思路,Mancoridis等[6]提出了软件模块化质量(Modularization Quality, MQ)的评价指标,并被广泛采用。然而采用MQ作为进化算法的适应函数存在一个重要缺点:很容易造成孤立簇(Isolated cluster),即一个子系统只包含一个模块的现象[7]。针对这个问题,本文提出了一个新的改进型软件模块化衡量指标(Improved Modularization Quality, IMQ),以该指标作为进化算法的适应函数可以有效抑制孤立簇现象。
在算法方面,软件模块化本质上是一个聚类问题,解决该问题的算法可分为两类:一类需要事先根据先验知识确定模块数目(通常也称为聚类数目),例如K-means算法[8]和k-mediods算法[9]。这类算法操作简单且效率较高,但其缺点是要在优化之前就确定模块数目,即:模块数目不是决策变量。另一类算法将模块数目也作为决策变量,比如:Bandyopadhyay等[10]提出的遗传算法(Genetic Algorithm, GA)以随机的方式从染色体中找出有效质心来动态决定模块数目;Omran等[11]提出的K-means和粒子群相结合的算法;Maqbool等[12]为软件架构重组设计的层次聚类方法。为了使算法具有更好的实用性,本文重点关注第二类算法。
传统聚类问题多以距离为量化的基础,软件模块化问题以特定的软件工程量化指标为模块化依据,使得该问题难以求解,因此进化算法和启发式算法已经成为解决软件模块化问题的主流方法。第一次运用遗传算法来解决软件模块化问题是Mancoridis等[6]。随后,Harman等[13]将模块的颗粒度融入适应度函数的测量中,并基于此设计了针对软件模块化问题的启发式算法。值得重点说的是由Mitchell等[14]在2008年设计的融合模拟退火机制的多点爬山算法,对比实验结果证明:该多点爬山算法能找到高质量的模块化方案。基于其研究工作的重要意义不仅在高效算法的设计,而且在于Mancoridis和Mitchell开发了一个基于搜索的软件模块化工具(Bunch),该工具集成了多种进化算法和启发式方法,该领域其他研究工作广泛采用Bunch工具中的算法作为BenchMark进行对比实验[6]。同时,为了兼顾多个目标(如:最大化MQ指标的同时、最小化的孤立簇个数),很多研究人员运用多目标优化算法来解决软件模块化问题。如:Mkaouer等[15]所采用的NSGA-Ⅲ算法,以及Praditwong等[7]提出的多目标方法。虽然多目标进化算法在搜索Pareto解方面有一定优势,但是也正是因为Pareto最优,使得多目标算法往往要消耗很多的资源和时间搜索高质量的解。随着问题规模的增加,搜索空间的迅速膨胀,低效率限制了该类方法的应用。本研究不是从多目标优化算法入手,而是将研究重点放在设计本身具备提高MQ和抑制孤立簇的指标,并设计符合问题特点的高效进化算法来验证其寻优能力和鲁棒性。本文工作主要有以下几点:
1)提出一个新的软件模块化度量指标IMQ,该指标不仅能够平衡内聚和耦合的关系,而且能够有效降低孤立簇个数;
2)建立以最大化IMQ为目标的软件模块化问题的数学模型。
3)设计符合问题特点的改进遗传算法(Improved Genetic Algorithm, IGA)求解提出的数学模型,该算法的重要特点是运用了基于边收缩方法的启发式策略生成种子解,提高了算法的寻优能力和鲁棒性。
4)将IGA与基于GNE(Group Number Encoding)遗传算法[7]和融合模拟退火机制的改进爬山(Improved Hill Climbing, IHC)算法——多点爬山算法[14]进行对比实验,用t检验和Cohen’s d index规模值[2]的方式来检验算法对比的结果。结果显示IGA相对于该两种算法具有更好的寻优能力和鲁棒性。
1 问题描述
一个软件系统中软件构件之间的关系可以使用模块依赖图(Module Dependency Graph, MDG)[2,7,14]抽象描述。MDG中的每个节点代表了每个软件构件,边代表两构件之间的相互关联程度。软件模块化是基于软件构件的关联程度对软件系统进行自动划分并得到模块化较好的聚类目标的过程。不同的模块化优化模型中的目标就是以构件之间的关联度为依据构造的,比如:内聚、耦合或者两者之间的特定关系。其中,内聚指的是一个模块内软件构件之间的相互联系;耦合衡量的是不同模块之间软件构件的相互联系。本章将提出一个新的软件模块化的量化指标和软件模块化问题的数学规划模型。
1.1 IMQ指标
早期的研究工作采用高内聚和低耦合来判断软件设计质量的标准[2,6-7,14-15]。高内聚意味着子系统中模块之间的联系越大越好;低耦合意味着不同子系统之间的联系越少越好。然而,一味地追求高内聚和低耦合这两个目标,最后会得到一个“完美方案”,即一个子系统包含了所有模块。显然这与实际要求不符,因此,近年来,学者们提出在内聚和耦合之间作出合理的平衡。Mancoridis等[6]提出的限制过度耦合且不会完全消除耦合的模块化质量指标MQ,能平衡高内聚和低耦合这两个目标;但是MQ指标忽略了系统中孤立簇的存在,明显增加了系统的维护成本,并不是良好的软件模块划分方案。针对该问题,Pradiwong等[7]在2011年提出的软件模块化的多目标算法MCA中,将最小化孤立簇的个数作为其中的一个目标。区别于其研究工作,为了避免多目标优化寻找Pareto最优的低效率,本文提出了一个新的软件模块化指标,运用该指标作为进化算法的适应函数,可以在实现内聚和耦合平衡的同时,有效抑制孤立簇现象的发生。
一个模块依赖图G可以简单记为(V,E)二元组,并用|V|表示顶点的个数,用|E|表示边数。当一个模块依赖图G=(V,E)被划分成k个子图,IMQ的计算公式如下:
(1)
CFi代表第i(1≤i≤k)个子图的聚簇因子,M是孤立簇的个数。其中聚簇因子CFi的计算公式如下:
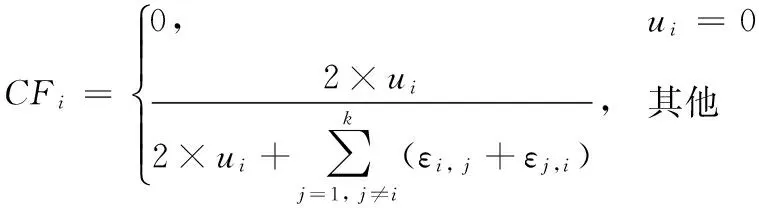
(2)
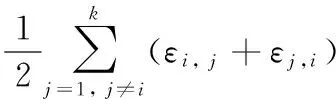
1.2 数学规划模型
以IMQ为基础,为了建立数学规划模型,引入数学符号如表1所示。

表1 模型中数学符号的定义Tab. 1 Definition of symbols in the model
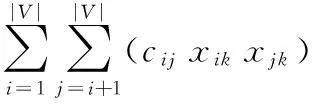
基于以上数学符号,软件模块化问题的数学规划模型可表示为:
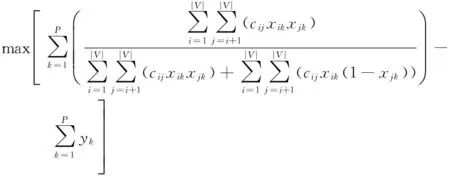
(3)
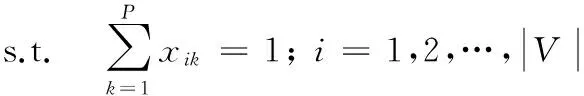
(4)
(5)
(6)
xik∈{0,1};i=1,2,…,|V|,k=1,2,…,M
(7)
yk∈{0,1};k=1,2,…,M
(8)
P∈{1,2,…,|V|}
(9)
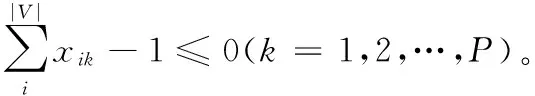
通过分析模型(3)~ (9),可知由于如下因素综合导致无法无法多项式时间内求解该类模型:
1)决策变量xik和yk为二进制决策变量;
2)目标函数(3)分子和分母中均包含决策变量,并且含有决策变量的二次项;
3)P作为整数决策变量出现在模型中导致模型更难求解;
4)该问题可以规约为图论中已经被证明为NP-hard问题[16]的最小切问题。
因此,本文重点设计一种在可接受时间内搜索高质量模块化方案的改进遗传算法。
2 改进的遗传算法
为克服传统算法局部搜索能力较差、极易陷入局部最优的缺点,本文设计改进遗传算法IGA来求解软件模块化问题。IGA的适应度函数采用IMQ指标。IGA的改进主要体现在两个方面:一个是用启发式策略生成初始种群;另一个是采用基于相似度的竞争和选择机制。
2.1 个体编码
本文采用分组编码(Group Number Encoding, GNE)方式,即:染色体中的位置表示软件构件的编号,每个位置上的整数值表示对应的模块编号,相同整数代表对应位置上的软件构件被划分在同一模块中。如x=[1,1,1,1,2,2,2,3,3]代表着一个软件模块化方案,该方案将9个软件构件划分到3个模块中,构件1,2,3和4被划分到模块1中;构件5,6和7被划分到模块2中;构件8和9被划分到模块3中。
2.2 生成初始种群的启发式算法
启发式算法以IMQ值最大化为目标,算法的思想如下:最初,所有顶点都未经融合,将所有顶点当作一个独立的子图;然后,每次迭代选择收缩边权最大的边,并融合该边两端的顶点被当作一个新的子图,此时所有未经融合的顶点同样被当作是一个子图,每一步都更新模块划分方案,直到最后所有顶点融合在一起。在这个收缩边和顶点融合过程中,计算每一次迭代后IMQ的值,取IMQ最大的状态图作为备选模块划分方案。迭代过程中,如果存在多个权重最大的边,以轮盘赌的方式选取其中一个继续迭代过程。此随机选择方式能够保证初始种群的多样性。
以图1直观解释启发式算法。每个顶点旁的矩形中的数字表示该顶点的内聚值,最初每个顶点的内聚值均为0。图标题中的P代表每个过程中的模块数,M代表每个过程中的孤立簇的个数。每个图中虚线中的两个点表示下一步中要融合的点。例如图1(a)阶段,顶点4和顶点5融合在一起形成了一个新的子图,该子图的内聚为顶点之间的边权与两个原顶点的内聚之和。将剩下的所有未经融合的顶点看作另一个子图,所以该状态的模块数是2,孤立簇个数为0。此时,由于存在两个最大权重的边,即:顶点1和顶点3之间的边,顶点7和顶点8之间的边,边权都为8,则以轮盘赌的方式选取一个,本示例选取了顶点1和顶点3作为下一步融合的两个点。
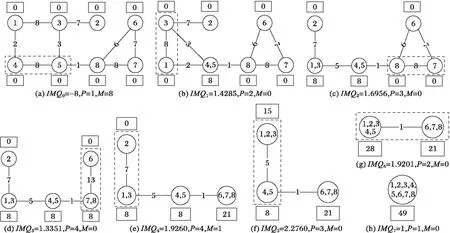
图1 启发式算法示例 Fig. 1 Examples of heuristic algorithm
通过记录了迭代过程中每个状态的IMQ的值,在图2中绘出IMQ的变动情况。从图2中可以看出,在合并顶点的过程中IMQ的值是在不断变动的,其中IMQ5的值最大,为2.276 0。IMQ5对应于图1(f)所示的状态,就是启发式算法找到的软件模块化的方案,即:(1,2,3),(4,5)和(6,7,8)。
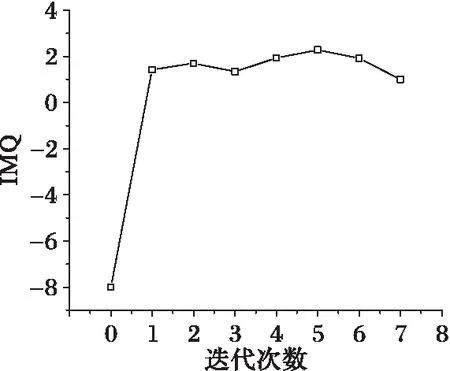
图2 IMQ迭代变动情况 Fig. 2 IMQ change with iterations
该启发式算法为IGA的初始化种群策略的重要组成部分:即将该启发式算法得到的近似最优解作为种子植入到初始种群中,再用遗传算法进一步提高解的质量。传统遗传算法在实际应用过程中经常会陷入局部最优解,这些现象的产生主要是因为进化过程中个别较优个体过早地在种群中大量繁殖,种群多样性大大降低。为避免该现象,IGA的初始种群中一部分的个体由启发式算法生成,另一部分个体随机生成,以保证初始种群的多样性,具体组成比例由实验来确定。
2.3 改进的竞争机制
本文针对传统遗传算法的早熟和多样性差的特点[17],在两点交叉算子的基础上提出了一种基于相似度的竞争和选择机制。在进行交叉操作的时候,两个父代之间的相似度越大,越不易于新的基因型的产生[18];所以该机制就在进行交叉操作之前,先检验两个父代之间的相似度。相似度等于基因串对应位置的基因相同的个数除以基因串的长度。以整数编码为例,设两个父代个体X,Y为:
(10)
其中:xi∈Z,yi∈Z,i=1,2,…,m。
则两个个体之间的相似度p(X,Y)为:
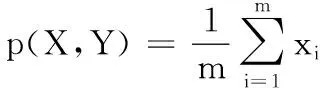
(11)
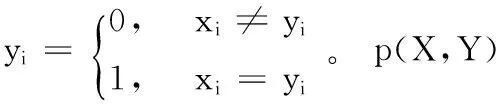
根据IGA的算法流程,其主要步骤如下:
1)运用启发式策略生成一半初始种群(为了提供高质量的初始解),另外一半用随机的方法生成(为了保证初始解的多样性)。
2)计算种群中每一个个体的适应值。
3)按照一定的规则选择进行下一代的个体,该规则与个体的适应值相关。本文运用轮盘赌的选择方法。
4)根据本文提出的相似度的计算规则,计算父代的相似度p。如果p<0.8,则进行交叉操作,否则返回3)。
5)按照一定的变异概率Pm进行个体变异。
6)判断现在的状态是否满足停止条件,如果满足就进入下一步,否则返回3)。
7)输出相关信息,包括最优解和运行的时间等信息。
3 实验数据与方法
本文实验主要解决以下三个问题:1)IMQ指标能否有效减少孤立簇的数目;2)对比IHC算法和基于GNE遗传算法(简称GNE算法),IGA是否能找到质量更高的解;3)对比IGA、IHC和GNE算法的求解的鲁棒性。
3.1 数据来源
实验主要分为两部分:第一部分是基于真实数据的实验,第二部分是基于仿真数据的实验。在第一部分中,本文所用实例来源于Mancoridis和Mitchell开发的软件模块化工具Bunch软件,且被许多学者采用,如Kumari等[2]、Praditwong等[7]。MDG的顶点数从27~148,边数从75~1 745。16个实例的具体信息如表2所示。
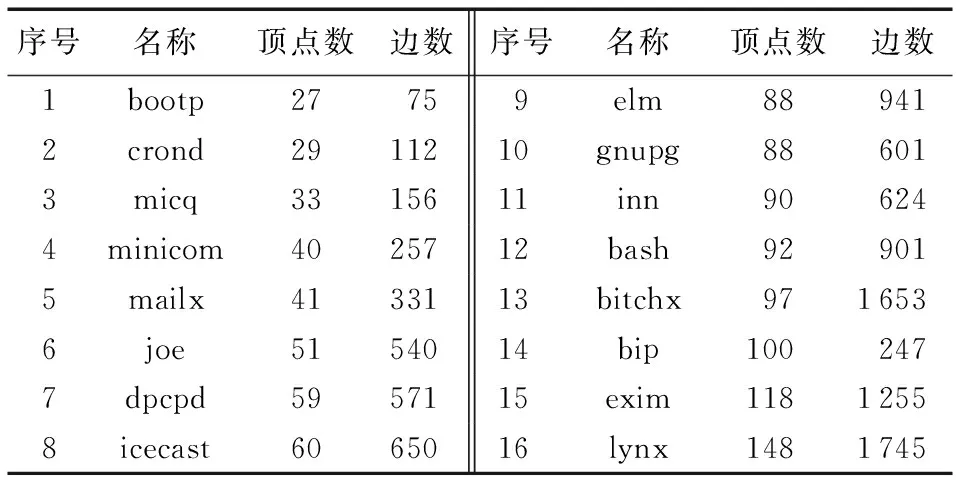
表2 实验数据来源Tab. 2 Data source used in the experiment
3.2 实验内容
每组实验中,将IGA分别与GNE算法和IHC算法的解的质量作对比。为了有效跳出局部最优解,IHC算法集成了模拟退火机制。该算法已集成在著名的Bunch软件中,是同类研究的重要对比算法[14]。
Bunch中IHC算法设置了一个阈值η(0%≤η≤100%) 来计算在每次爬山算法迭代过程中需要考虑的相邻节点的最小值[7]。若相邻节点的个数少于200,则η取75%;若大于200,则将需要考虑的相邻节点的个数设定为200。这样的设定无疑会增加算法的运行时间,但同时也会增加找到更好的解的概率。IHC采用模拟退火机制避免陷入局部最优解,即算法以一定的概率P(A)接受质量稍差的解,公式如下:
(12)
其中k表示迭代的次数。由于本文提出了对软件模块化质量的改进方案,当使用IMQ指标时,将IHC的MQ指标替换为IMQ指标即可。连续性降低的比率α被设置为0.9,初始的温度T(0)=100。此外初始爬山点的个数设置为10个。以上IHC参数设置的合理性,请参考文献[14]。
首先,为了保证初始种群的多样性, IGA的初始种群中一部分的个体由启发式算法生成,具体多少比例的初始种群是由实验来确定的。本文一共设置了三组实验。由启发式算法和随机方式生成初始种群的比例分别为(1/4,3/4),(1/2,1/2),(3/4,1/4)。基于真实数据,分别记录下以IMQ为软件模块化指标的IGA重复30次实验的平均值。
对比实验中,分别用GNE算法、IGA和IHC对每个实例进行模块化划分。由于进化算法的机制中存在随机因素,每次运行算法得到的结果往往不同,仅一次运行结果并不能说明问题。所以在实验中,给定一个实例,每个算法运行30次,记录每次搜索到的解。为了公平比较,实验程序确保三种算法运行足够长时间,并且运行相同时间。该时间由反复实验确定,为60 s。为了对比IMQ指标抑制孤立簇的效果,针对真实数据,本文分别用IMQ指标和MQ指标进行实验,记录下三个算法每次进行模块化划分后的孤立簇的数目,并用IMQ指标做仿真实验对比三个算法在处理大规模问题时的性能。
运行实验的平台配置为:3.2 GHz Intel Core i5- 3470 CPU (4×256 KB L2 缓存和6M L3 缓存),DDR3 8 GB内存。遗传算法的其他参数的设定是通过反复实验确定的,具体参数取值:种群规模=100,交叉概率Pc=0.8, 变异概率Pm=0.2。
3.3 分析方法
为验证新的软件模块化指标IMQ抑制孤立簇的效果,针对每个实例,分别用MQ指标和IMQ指标作为三个算法的优化目标重复实验30次,对比得到的最优解的孤立簇数目的平均值。
为检验IGA的寻优能力,实验对比30次实验所取最优解的平均值和标准差。由于实验主要检验IGA的性能,本文分别比较IGA和GNE算法,IGA和IHC的实验结果。所有结果均用独立样本双尾t检验进行统计分析,置信水平为95%。检验是用T分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著[19-20]。由于已知数据的均值和标准差,本文用的是统计分析常用的参数化t检验,而不是非参数t检验。当t检验的p值小于0.05的时候,说明两个样本的均值在95%置信水平内存在显著的差异。此外,本文还计算了效应值Cohen’s d index,以便于解释结果的显著性。Cohen’s d index常用在T检验中表示两个均值之间标准化差异的效应值[2]。据经验,效应值为0.20左右表示显著性较小; 0.50左右表示显著性中等,0.80左右表示显著性较大。
4 结果及分析
4.1 基于真实数据的实验
首先,本文通过实验来确定由启发式算法组成初始种群的比例。分别进行了三组对照实验,由启发式算法和随机方式生成初始种群的比例分别为(1/4,3/4),(1/2,1/2),(3/4,1/4)。最后由IGA运行30次得到的IMQ的平均值如表3所示。从结果可以看出,当初始种群组成比例为(1/2,1/2)时,IGA得到的IMQ值在16个真实案例里面有9个是最高的,优势明显。当初始种群的组成比例为(1/4,3/4)时,启发式算法组成的初始种群的比例偏低,其优势显示不出;当初始种群的组成比例为(3/4,1/4)时,启发式算法组成的初始种群的比例偏高,初始种群结构单一,多样性无法保证,IGA容易陷入局部最优解。实验结果证明,由启发式算法和随机方式生成初始种群的比例分别为(1/2,1/2)时,IGA搜索最优解的效果最好。之后的对比实验中IGA初始种群都是一半由启发式算法生成,而另一半由随机方法生成。
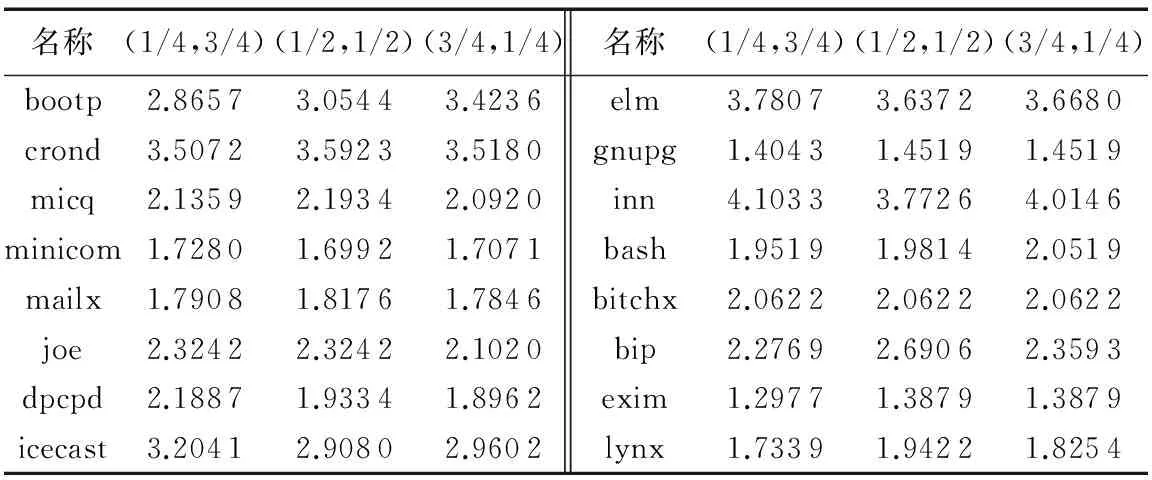
表3 初始种群不同组成比例下IGA得到的IMQ值Tab. 3 IMQ value obtained by IGA under different composition of initial population
三个算法分别用两个指标得到的最优解的孤立簇数目的平均值如表4所示。由表4可以看出,IMQ指标在降低孤立簇数目上效果显著:在以IMQ为目标函数的实验中,GNE算法和IGA针对每个实例的30次实验所得到的孤立簇数目的平均值均为零,均小于以MQ为目标函数的结果值;且在IHC算法得到的结果中,IMQ指标的孤立簇的平均数目比MQ指标的少。由此,本文剩下的实验部分采用能有效减少孤立簇数目的IMQ指标作为算法的寻优目标。另外,在以MQ为目标函数的实验中,IGA降低孤立簇的效果最显著,孤立簇的平均个数最少,GNE最差。三种算法的性能对比还需通过进一步的实验验证。

表4 两个软件模块化指标的孤立簇数目对比Tab. 4 Comparison of the number of isolated clusters by two software modularization qualities
除此之外,实验得到了三个算法针对表2中每个实例搜索到的最优解IMQ值的平均值及标准差以及T检验的p值和效应值,本文对三个算法进行两两比较,比较结果如表5所示。
从表5中可得如下结论:
1)从每个实例的均值比较来看,IGA找到的最好解的质量均优于GNE算法和IHC算法,并且所有实例里面的p值都远远小于0.05,说明在95%的置信水平下,IGA在相同的时间内取得解的质量要明显优于GNE算法和IHC算法。相比之下,IHC算法重复运行30次得到的IMQ的平均值最低,说明IHC算法在搜索过程中容易落入局部最优解,具有短视的缺点。
2)对于每个实例的标准差,IGA在所有实例中的标准差都比IHC算法的标准差要小。在与GNE算法的比较实验中,IGA在16个实例中有13个实例的标准差比GNE算法的小,除了“inn”“bip”“exim”。也正说明了IGA的鲁棒性比较高,每次运行结果可行度较高。
3)在所有的16个实例的实验中,效应值的绝对值都大于0.8,说明两种算法得到结果的均值差距足够大,进一步说明了IGA的优势很显著。
4.2 基于仿真数据的实验
虽然是基于实际数据,但以上对比实验中的问题规模偏小,且不便验证MDG密度的增加对结果的影响,为了对比三个算法在处理大规模问题时的性能,本文设计了基于仿真数据的实验,实验结果如表6所示。通过观察数据,可得到以下结论:
1)在这30个算例中,IGA总能够找到比GNE算法和IHC算法更高的IMQ值,说明IGA能有效跳出局部最优解,在求解质量方面优于GNE算法和IHC算法。所有算例里面的p值都远远小于0.05,证明了在95%的置信水平下IGA得到的解的质量显著优于GNE算法和IHC算法。
2)尽管引入了模拟退火机制,IHC算法的解的质量甚至不如GNE算法,原因是对于大规模问题,模拟退火机制也很难克服爬山算法的短视缺点;特别是在顶点数增加,图的密度增加的时候,IHC算法就可能得到较差的解。例如在|V|=300,|E|=33 637的案例9中,由于IMQ指标加入了对孤立簇的惩罚,IHC算法单次搜索到了负值,30次重复实验所得IMQ值的均值是0.9,说明该算法不稳定。
3)大多数情况下,IGA所得结果的标准差相对较小,说明IGA有较强的鲁棒性和稳定性,即:每次算法运行结果不会相差很大。
4)在所有的仿真数据的实验中,效应值的绝对值都大于0.8,说明了IGA的优势显著。
5)给定顶点数目,MDG密度的增加对IGA的鲁棒性影响不大,密度越高,IGA得到结果的标准差越小,但对IHC算法的鲁棒性影响较大。虽然MDG密度的增加对GNE算法的鲁棒性影响也不是很大,但是这是GNE算法过早收敛、陷入局部最优的结果。从IGA和GNE算法的对比结果中可以看出,IGA处理稀疏MDG的性能较优,得到IMQ的值比GNE算法得到的IMQ值高很多。相比之下,IGA处理稠密MDG的性能较弱,虽然得到的解的质量最高,但是与GNE算法得到的IMQ值越来越接近。现实中的软件系统大多是稀疏,Mitchell等[14]的研究提出软件系统的平均密度为17%,由此可见,IGA具有较强的实用性。
实验结果表明:相对于GNE算法和IHC算法,IGA能找到质量更高的解,且有更好的鲁棒性。
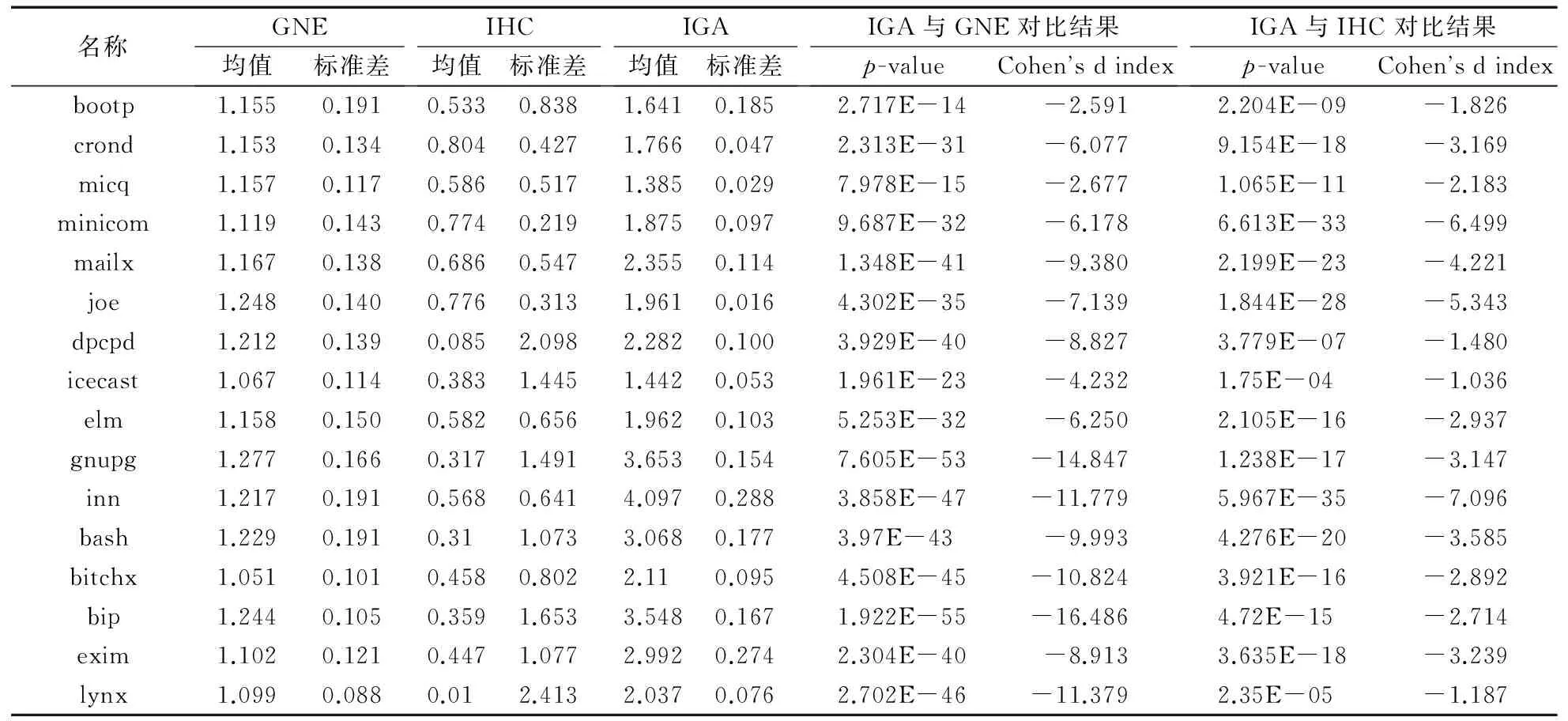
表5 GNE、IHC和IGA真实数据结果Tab. 5 Results of GNE, IHC and IGA on real data
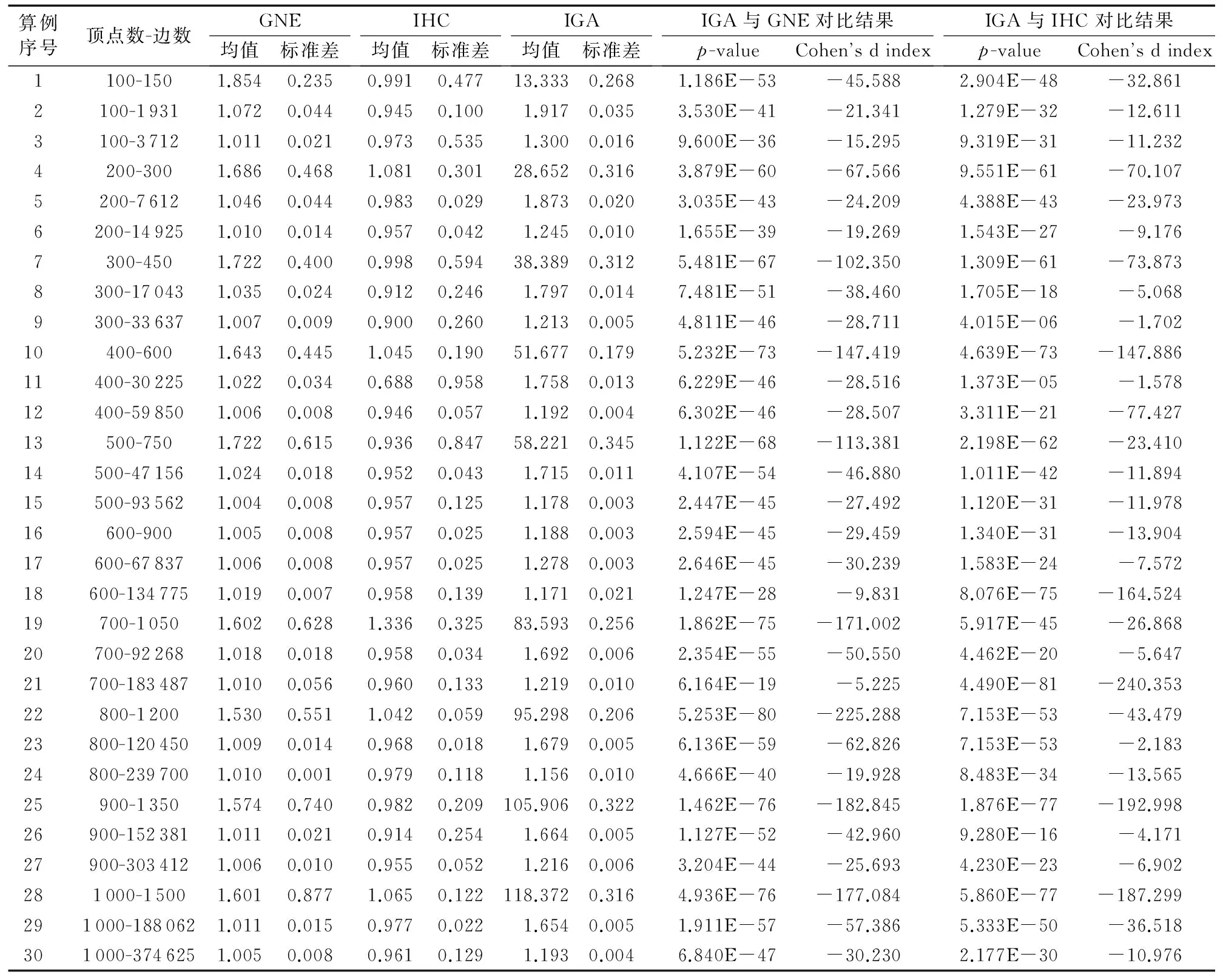
表6 GNE, IHC和IGA仿真数据结果Tab. 6 Results of GNE, IHC and IGA on simulated data
5 结语
本文运用基于搜索的方法来解决软件模块化问题,与传统的同类研究不同,本研究设计了相应机制抑制解中的孤立簇现象。研究工作提出一个新的软件模块化指标IMQ,并为抑制孤立簇的模块化优化问题建立了数学模型。最重要的是设计了IGA用于寻找得到更高质量的解,并通过两类对比实验,证明了IMQ指标能够有效减少孤立簇的数目,且IGA相比IHC算法和GNE算法具有更强的寻优能力和更好的鲁棒性。
后续研究工作计划将从如下几个方面展开:
1)运用改进的启发式初始种群生成策略、高级的交叉方式和变异方式改进其他进化算法,比如:粒子群、文化基因算法等,并与IGA比较,分析各自优缺点,进一步完善改进方案。
2)考虑多目标优化算法来平衡内聚和耦合两个指标,怎样将自适应算法与多目标优化算法相结合解决同类问题。
3)运用启发式初始种群生成策略和基于相似度的竞争和选择机制改进传统多目标优化算法,比如SPEA-Ⅱ算法、NSGA-Ⅲ算法等。
参考文献(References)
[1] HARMAN M. The current state and future of search based software engineering [C]// FOSE ’07: Proceedings of the 2007 Future of Software Engineering. Washington, DC: IEEE Computer Society, 2007: 342-357.
[2] KUMARI A C, SRINIVAS K. Hyper-heuristic approach for multi-objective software module clustering [J]. Journal of Systems and Software, 2016, 117: 384-401.
[3] STEVENS W P, MYERS G J, CONSTANTINE L L. Structured design [J]. IBM Systems Journal, 1974, 13(2): 115-139.
[4] HARRISON R, COUNSELL S J, NITHI R V, et al. An evaluation of the MOOD set of object-oriented software metrics [J]. IEEE Transactions on Software Engineering, 1998, 24(6): 491-496.
[5] TUCKER A, SWIFT S, LIU X, et al. Variable grouping in multivariate time series via correlation [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2001, 31(2): 235-245.
[6] MANCORIDIS S, MITCHELL B S, CHEN Y, et al. Bunch: a clustering tool for the recovery and maintenance of software system structures [C]// ICSM ’99: Proceedings of the 1999 IEEE International Conference on Software Maintenance. Washington, DC: IEEE Computer Society, 1999: 50-59.
[7] PRADITWONG K, HARMAN M, YAO X, et al. Software module clustering as a multi-objective search problem [J]. IEEE Transactions on Software Engineering, 2011, 37(2): 264-282.
[8] MacQUEEN J. Some methods for classification and analysis of multivariate observations [C]// Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley: University of California Press, 1967: 281-297.
[9] HADI A S. Finding groups in data: an introduction to chster analysis [J]. Technometrics, 1992, 34(1): 111-112.
[10] BANDYOPADHYAY S, MAULIK U. Genetic clustering for automatic evolution of clusters and application to image classification [J]. Pattern Recognition, 2002, 35(6): 1197-1208.
[11] OMRAN M G H, SALMAN A, ENGELBRECHT A P. Dynamic clustering using particle swarm optimization with application in image segmentation [J]. Pattern Analysis & Applications, 2006, 8(4): 332.
[12] MAQBOOL O, BABRI H. Hierarchical clustering for software architecture recovery [J]. IEEE Transactions on Software Engineering, 2007, 33(11): 759-780.
[13] HARMAN M, HIERONS R M, PROCTOR M. A new representation and crossover operator for search-based optimization of software modularization [C]// GECCO ’02: Proceedings of the Genetic and Evolutionary Computation Conference. San Francisco, CA: Morgan Kaufmann Publishers, 2002: 1351-1358.
[14] MITCHELL B S, MANCORIDIS S. On the evaluation of the Bunch search-based software modularization algorithm [J]. Soft Computing, 2008, 12(1): 77-93.
[15] MKAOUER W, KESSENTINI M, SHAOUT A, et al. Many-objective software remodularization using NSGA-Ⅲ [J]. ACM Transactions on Software Engineering & Methodology, 2015, 24(3): Article No. 17.
[16] AKBALIK A, HADJ-ALOUANE A B, SAUER N, et al. NP-hard and polynomial cases for the single-item lot sizing problem with batch ordering under capacity reservation contract [J]. European Journal of Operational Research, 2017, 257(2): 483-493.
[17] 杨劼,高红,刘涛,等.基于改进遗传算法的泊位岸桥协调调度优化[J].计算机应用,2016,36(11):3136-3140. (YANG J, GAO H, LIU T, et al. Integrated berth and quay-crane scheduling based on improved genetic algorithm [J]. Journal of Computer Applications, 2016, 36(11): 3136-3140.)
[18] 范青武,王普,高学金.一种基于有向交叉的遗传算法[J].控制与决策,2009,24(4):542-546. (FAN Q W, WANG P, GAO X J, et al. Improved genetic algorithm based on oriented crossover [J]. Control and Decision, 2009, 24(4): 542-546.)
[19] ARCURI A. A practical guide for using statistical tests to assess randomized algorithms in software engineering [C]// ICSE ’11: Proceedings of the 33rd International Conference on Software Engineering. New York: ACM, 2011: 1-10.
[20] PRADITWONG K. Solving software module clustering problem by evolutionary algorithms [C]// JCSSE 2011: Proceedings of the Eighth International Joint Conference on Computer Science and Software Engineering. Piscataway, NJ: IEEE, 2011: 154-159.
This work is partially supported by the National Natural Science Foundation of China (71302051).
MULifeng, born in 1978, Ph. D., lecturer. His research interests include search-based software engineering, evolutionary algorithm design.
WANGFangyuan, born in 1994, M. S. candidate. Her research interests include search-based software engineering, evolutionary algorithm design.

