结合概率矩阵分解的混合型推荐算法

杨丰瑞，郑云俊，张 昌

(1.重庆邮电大学 通信新技术应用研究中心，重庆 400065; 2.重庆重邮信科(集团)股份有限公司，重庆 401121)

0 引言

在信息化时代，我们很难在短时间内从大量的数据中选择有用的信息，而传统的推荐算法已经不能满足用户对有效信息的需求。在这种复杂的数据背景下，基于个性化的推荐算法成为一个热点的研究主题[1]。

如今推荐系统一直是帮助用户在短时间内获取有效信息的最有用的工具之一。越来越多的电子商务和视频网站如亚马逊[2]、Twitter[3]和YouTube[4]制定了各自的推荐系统，以促进销售和提高用户体验。亚马逊的CF(Collaborative Filtering)算法比传统的CF算法，大大节约了资源。Twitter帮助用户找到合适关注的账号，提升用户参与度，吸引更多新用户来到Twitter平台。YouTube使用用户的观看历史、搜索记录以及用户统计信息为用户推荐视频。

本文的主要工作为：提出了结合特征传递和概率矩阵因式分解(feature Transfer and Probability Matrix Factorization, TPMF)的社交网络推荐算法,其主要思想是融合个人潜在特征、社会潜在特征和推荐项目间的关联特征属性，将三者结合在统一的推荐框架中，将实验数据应用到所提出的推荐算法中，分析了推荐的各方面性能以及实验参数对推荐性能的影响。

1 相关工作

推荐系统通过分析用户购买和评级的历史记录来进行预测和推荐。协同过滤[5-6]是个性化推荐中最成功的技术之一，使用用户的大量评分记录来预测目标用户将会选择哪些项目已被广泛研究[7-9]，但算法存在稀疏性问题、评级数据不平衡和冷启动问题，很难向新用户或者评价项目少的用户提供推荐服务。矩阵分解技术[10]是解决数据稀疏和不平衡问题广泛使用的方法之一，如基于联合概率矩阵分解(Union Probability Matrix Factorization, UPMF)的推荐算法[11]、郭磊等[12]提出了StrengthMF和InfluenceMF，利用信任关系和兴趣偏好通过共享的特征空间建模。矩阵分解技术通常从稀疏用户评分矩阵中学习用户和项目的潜在特征，根据用户和项目潜在特征预测非购买项目的评级。虽然这种方法已经取得了显著成果，由于新用户缺乏辅助信息或用户很少被评级，仍遭受冷启动问题。许多社交网站如Facebook和Twitter[13]已经成为满足人们的好友交互与沟通的平台，可以从社交网络中的所有的朋友列表中提取直接信任网络[14]，这是一个解决冷启动问题的可用辅助数据，提高推荐质量。

以上的推荐算法取得了不错的推荐效果，但没有考虑推荐项目之间的关联关系。本文提出的算法融合社交网络、评级记录中的信任信息和推荐项目之间的关联信息，以学习项目潜在特征向量，用户个人潜在特征向量和社会潜在特征向量；特征传递用于从受信任的人获得社会影响力，自适应权重用于决策个人潜在特征和社交潜在特征对用户的影响程度。基于以上内容，本文提出了一种新型的混合型推荐算法。

2 TPMF算法流程

本章就用户项目评分矩阵、用户社交潜在特征矩阵和推荐项目之间的关联关系矩阵进行描述和细化，将这三个矩阵融合在统一的推荐框架下，实现推荐系统的性能更优化。

2.1 用户项目评分矩阵分解

在推荐算法中，用户项目评分矩阵R=[rij]m×n表示将m个用户对n个项目的评分关系用矩阵R表示。rij表示用户i对项目j的评分，通常rij的取值范围被限定在区间[Rmin,Rmax]中。在本文中，为了不失一般性，通过使用映射函数f(x)=(x-Rmin)/(Rmax-Rmin)将所有的用户对项目的评分值映射到区间[0,1]内。评分值rij越高，表示用户i对项目j的满意度越高，如用户i尚未对项目j进行评分，则相应的rij=0。通过矩阵分解可以将用户项目评分矩阵R∈Rm×n分解为两个矩阵U∈Rm×l和V∈Rn×l，其中l维行向量Ui和Vj代表了用户i的潜在特征向量和项目j的潜在特征向量，将用户项目评分矩阵R的条件概率定义为：

(1)

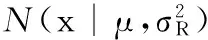
(2)

(3)

根据贝叶斯推理，潜在变量用户U和项目V的后验概率为：

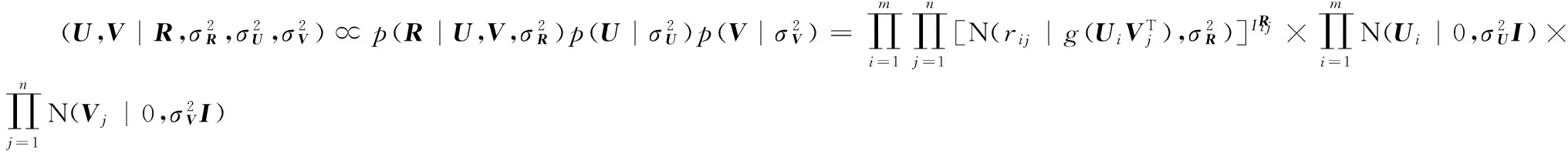
(4)

相应的模型如图1所示，它是概率矩阵分解(Probability Matrix Factorization, PMF)的模型。根据方程式(4)可以从用户项目评分矩阵中学习用户和项目的潜在特征向量。

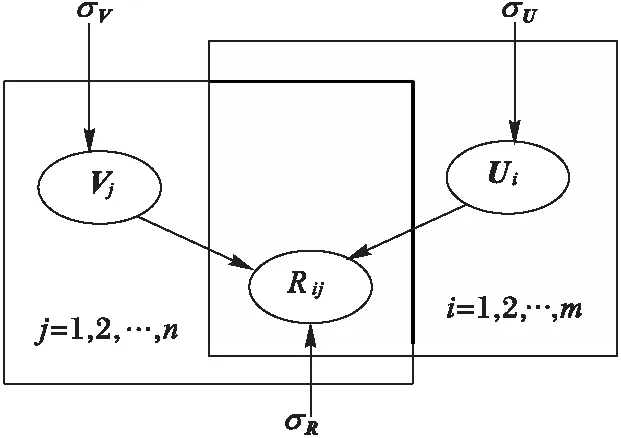
图1 概率矩阵分解的图形模型 Fig. 1 Graphic model of probability matrix factorization

2.2 用户社交潜在特征

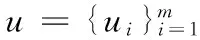
对于每个用户，向量Ui代表个人潜在特征，通过由矩阵Z∈Rm×l的行向量的l维向量Zi表示社交信任网络中的社交潜在特征。

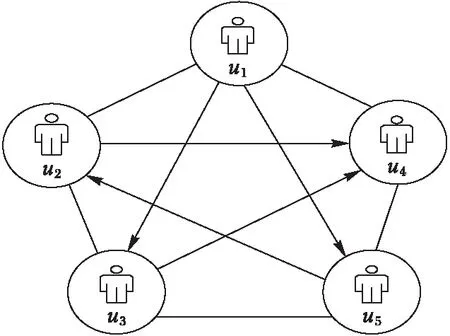
图2 社交信任网络模型 Fig. 2 Social trust network model

由于特征转移，用户i的行为受到其社交网络信任用户的影响，因此，用户i的社会潜在特征依赖于社交信任网络中用户的个人潜在特征。社交潜在特征矩阵Z可以通过个人潜在特征U和信任矩阵S来进行推导，这就是此算法中“特征传递”的基本原理。对于社交潜在特征矩阵，服从均值为0的高斯先验分布可以防止过拟合：

(5)

由贝叶斯公式得，个人潜在特征U、社交潜在特征Z和信任矩阵S的后验概率为：

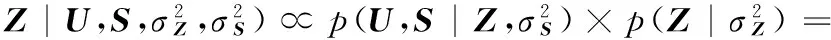
(6)

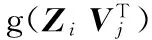
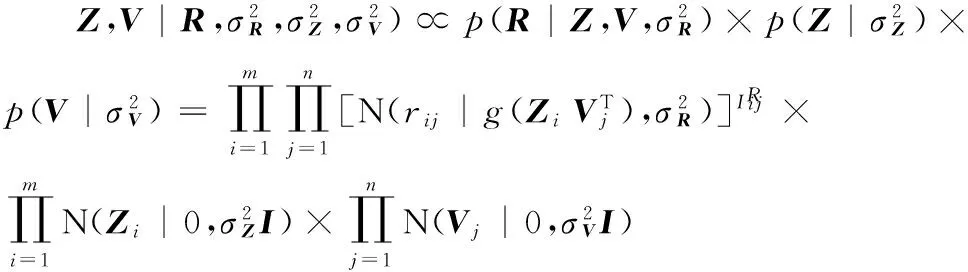
(7)

上述模型中，缺乏项目之间的关联关系矩阵，在优化的PMF算法基础上对算法进行改进，提出了结合特征转移和矩阵分解的推荐算法(TPMF)，融合推荐项目之间的关联关系进行推荐。

2.3 推荐项目关联关系矩阵

推荐项目间的关联关系用矩阵C表示。当推荐一本书籍给用户时，它会介绍此书籍的作者及其类型等。书籍分为是小说、记叙文还是自传等各种元素，这类描述项目特征的词可以认为是此项目的关键字。因此，对于给用户推荐的每个项目Vn={W1,W2,…,Wk}，Wi表示项目Vn的第i个特征。Wi=1表示项目Vn具有第i个特征，Wi=0表示不具有该特征，各个项目的集合可以组成一个内容特征矩阵。

根据各个推荐项目之间的内容特征矩阵，可以计算推荐项目之间的关联度，推荐项目Vi与Vj之间的关联关系权重可以表示为：

(8)

WVi,k=1表示推荐项目Vi有第k个特性，否则WVi,k=0。CViVj表示推荐项目Vi和Vj之间的特征关联关系，其值的大小决定了这两个项目关联的程度。C={CViVj}是一个(n×n)维的项目特征矩阵，CViVj≠0表示两个推荐项目之间有关联关系，否则CViVj=0，CViVj∈[0,1]表示了推荐项目间的关联关系权重的大小。

推荐项目Vi和Vj的特征关联关系可以从矩阵C中得到，特征关联关系矩阵C的后验概率分布可以表示为：

(9)

2.4 TPMF

根据用户个人潜在特征和社交潜在特征，可以为目标用户获得两个不同的评分预测。个人潜在特征和社交潜在特征将给用户推荐项目带来影响，为了自适应用户的个人潜在特征和社交潜在特征，设计了一个自适应权重α∈Rm×l，αi表示用户的个人潜在特征的影响，(1-αi)表示社交潜在特征对用户推荐项目带来的影响，假设α服从均值为1/2的高斯先验分布，则：

(10)

为综合U、Z、V、C、α，在社交网络中作出更好的推荐，所使用的概率模型如图3所示。

图3 TPMF概率模型 Fig. 3 TPMF probability model

通过贝叶斯推理得，U,Z,V,C,α的联合后验概率可以表示为：

(11)

U,Z,V,α的对数联合后验概率表示为：

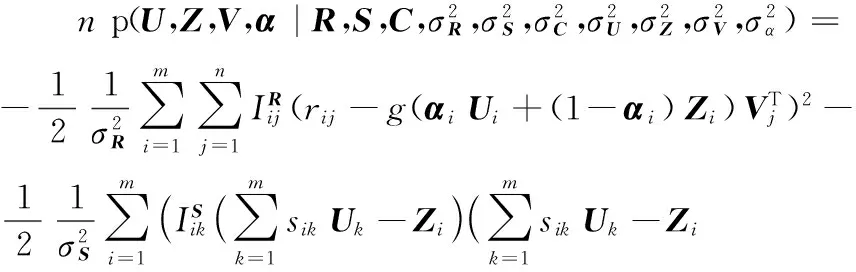
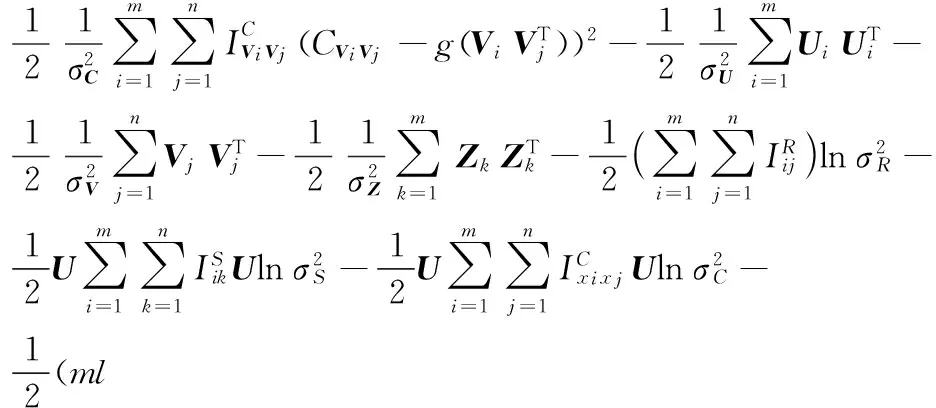
(12)

此处举例说明：某工厂有4条流水线生产同一产品，生产量分别占得比例为15%、20%、30%、35%，这4条流水线的次品率依次为0.05、0.04、0.03、0.02，现从出厂的产品中任取一件，求抽到次品的概率。

假设B={抽到次品}，Ai={抽到i条流水线的产品}，i=1,2,3,4,于是由全概率公式有：

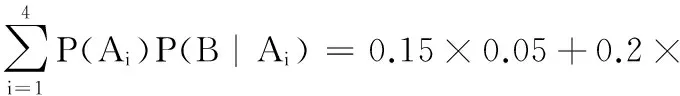
0.04+0.3×0.03+0.35×0.02=0.032 5

式(12)的原理亦是如此，此处取对数的目的是维持系统方差的恒定，提升推荐准确度。

ω是常数，最大化对数后验相当于最小化以下二次正则化项的平方误差之和函数：

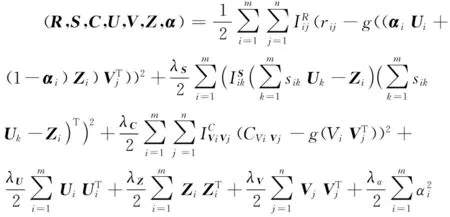
(13)

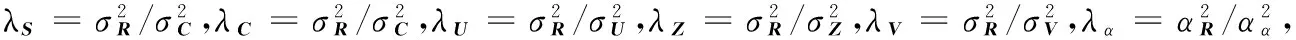
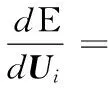
(14)

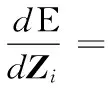
(15)

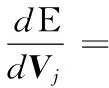
(16)

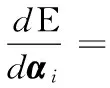
(17)

其中g′(x)=ex/(1+ex)2。

求函数f(x,y)=x2+xy+y的极值，此处的思想就是梯度下降。分别求x,y的梯度有：

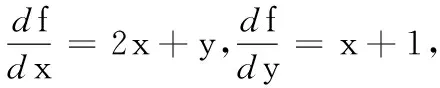
3 实验结果与分析

将本文提出的算法在实验数据集上与已存在的算法进行推荐性能的比较，以及不同的实验参数对实验结果的影响。

3.1 实验数据集

本文选取的实验数据集来自于Epinions网站和Ciao网站，数据集不仅包含用户评分记录，用户信任记录，还包含推荐项目间的关联关系信息。它是很受欢迎的产品评论网站，用户可以为已推荐的项目撰写评论和作出评分记录。这数据集中的每条评分记录包含[用户ID，项目ID，评分]，信任记录[用户ID1，用户ID2]，项目关联关系[项目ID1，项目ID2，关联度]。项目的所有评分记录在[1,5]，项目的关联度在[0,1]。Epinions数据集包含22 166个用户和296 277个项目，用户的评论信息有922 267条，Ciao数据集中包含7 375个用户，106 797个项目和284 086条用户评论信息。用户项目评分记录[25,2567,4.5]表示的是用户25对项目2567的评分是4.5，信任记录[23,35]表示用户23信任用户35，项目关联关系[256,672,0.7]表示的是项目256与项目672之间的关联度为0.7。

3.2 实验评估指标

为了评估算法的推荐性能，采用平均绝对误差(Mean Asolute Error, MAE)和均方根误差(Root Mean Square Error, RMSE)作为评估指标。

MAE是表示算法提出的预测值和真实值之间的平均绝对误差，不会出现正负抵消的情况，能更好地反映预测值误差的实际情况。RMSE是表示预测值与真实值偏差的平方与观测次数n比值的平方根，均方根误差对一组测量中的特大或特小误差反映非常敏感，能够很好地反映预测的精密度和数据集的离散程度。MAE和RMSE的定义如下：

(18)

(19)

其中:n表示的是预测的评分项目的个数，rij表示的是该算法计算出用户Ui对项目Vj预测值，xij表示的是用户Ui对项目Vj的真实的评分值。MAE值和RMSE值越小，说明提出算法的性能更好，算法的预测值更接近于实际值。

3.3 实验仿真结果对比

在此实验中，比较了UBCF[15]、TidalTrust[16]、PMF[17]、SoRec[18]和TPMF算法在Epinions和Ciao两数据集上面的推荐结果。其中的主要参数设置如下：λU=λZ=λV=0.01,λα=0.01,λS=0.1,λC=10,各算法的最大迭代次数为100。随机选择实验数据集的10%作为测试集，90%作为训练集，潜在的特征向量维度选取的是学术界实验常用的5维和10维的情况下的实验。实验结果如表1所示。

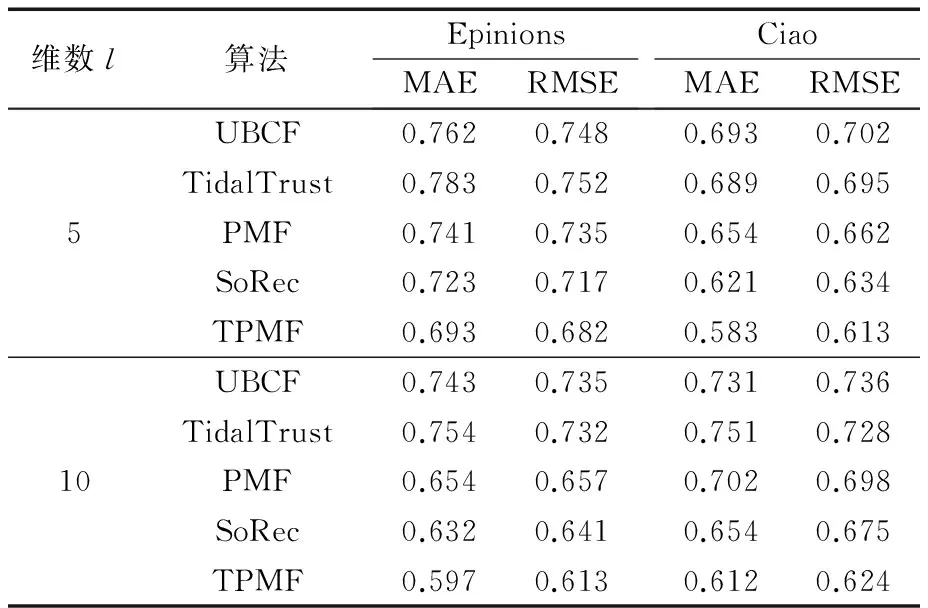
表1 实验结果对比Tab. 1 Comparison of experimental results

从表1中可以得到当维度为5维和10维时，本文所提出的算法在平均绝对误差和均方根误差上优于其他的4种推荐算法。以上5种算法分为两类，其中UBCF和TidalTrust属于非矩阵分解方法，PMF、SoRec和TPMF属于矩阵分解方法。可以得到，基于矩阵分解的推荐算法的推荐性能要优于基于非矩阵分解的推荐算法。其中基于矩阵分解方法的算法中，PMF算法仅仅是以用户项目评分矩阵作为推荐的主要依据，而SoRec算法是基于用户社交信任信息和用户项目评分记录来进行推荐，其推荐性能要优于PMF算法。本文提出的TPMF算法不仅联合用户社交信任信息、用户项目评分矩阵，增加了大数据环境下用户在社交网络中的特征传递和项目间的关联关系权重，推荐性能有较大程度的提升。其中MAE降低了4.1%～20.8%，RMSE降低了3.3%～18.5%。

在社交网络中，冷启动问题是指推荐系统中因为缺乏足够的历史数据而难以得到可靠结果。实验中使用学术界常用的定义，将评分项目数小于10的用户称为冷启动用户。随机从Epinions和Ciao数据集中选择10%的数据作为测试数据，90%作为实验训练集。在两个数据集中对用户冷启动的推荐结果如表2所示。

从表2中可得基于矩阵分解的推荐算法在解决冷启动问题上优于基于非矩阵分解的推荐算法。本文提出的TPMF算法融合了社交网络信任信息，并利用自适应权重α权衡个人特征和社交特征对用户推荐项目的影响，在解决冷启动问题上优于基于矩阵分解的推荐算法。MAE评估指标降低了1.6%～14.7%，RMSE指标降低了1.2%～9.7%。

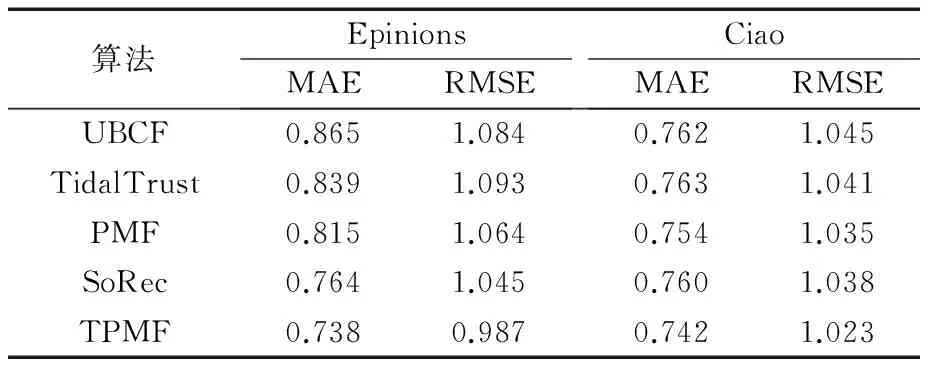
表2 不同算法中用户冷启动的实验对比结果Tab. 2 Comparison of experimental results of cold start for different algorithms

3.4 实验参数的影响

在本文提出的TPMF算法中，参数对推荐系统的性能有重要的作用和影响。参数λS控制着社交网络中用户之间的特征传递，λS的值越大，表示社交网络中用户之间的特征传递更容易，则用户的购买行为更容易受到影响。参数αi越大，表示用户的购买行为受个人潜在特征Ui的影响越大，则(1-αi)越小，用户的购买行为受社交潜在特征Zi影响越小。

图4显示了λS在MAE和RMSE这两个方面对两个数据集的影响。可以清晰地看出，MAE和RMSE随着参数λS的变化而发生着变化，当λS从0增加到0.1时，Epinions数据集的MAE先减小，达到一定阈值后又增加，RMSE也是先减小后增加。Ciao数据集也呈现出类似的变化，测试结果趋于稳定，证实了提出算法的鲁棒性很好。

4 结语

本文提出了一种新型的混合型推荐算法——TPMF算法，该算法以概率矩阵分解为框架，混合了社交信任关系、个人潜在特征、社交潜在特征、用户项目评分矩阵和推荐项目之间的关联关系，自适应权重α平衡个人潜在特征和社交潜在特征的影响。实验结果表明TPMF算法优于现有的基于矩阵分解的推荐算法，减少了冷启动问题对推荐系统的影响，提高了推荐的准确度。在当前大数据环境下，如何确认社交信任信息、个人潜在特征、社交潜在特征、用户项目评分矩阵以及推荐项目之间的关联关系在推荐系统中所占的权重值，得到更优的推荐结果，将是下一步的研究方向。

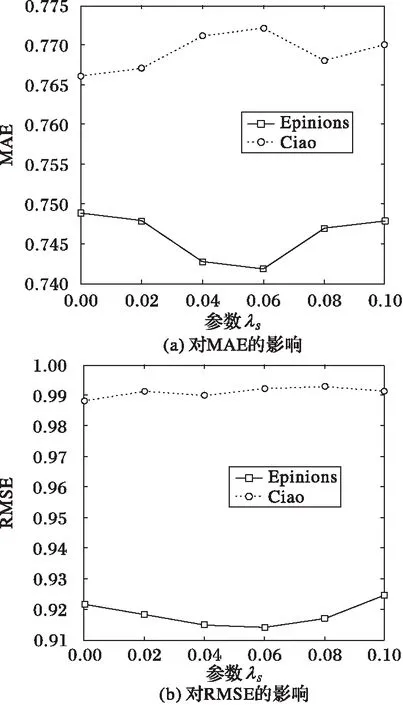
图4 参数λS对MAE和RMSE的影响 Fig. 4 Impact of parameterλS on MAE and RMSE

参考文献(References)

[1] DURAO F, DOLOG P. Improving tag-based recommendation with the collaborative value of wiki pages for knowledge sharing [J]. Journal of Ambient Intelligence Humanized Computing, 2014, 5(1): 21-38.

[2] LINDEN G, SMITH B, YORK J. Amazon.com recommendation: item-to-item collaborative filtering [J]. IEEE Internet Computing, 2003, 7(1): 76-80.

[3] ELMONGUI H G, MANSOUR R, MORSY H, et al. TRUPI: Twitter recommendation based on user’ personal interests [C]// International Conference on Intelligent Text Processing and Computational Linguistics, LNCS 9042. Berlin: Springer, 2015: 272-284.

[4] DAVIDSON J, LIEBALD B, LIU J, et al. The YouTube video recommendation system [C]// Proceeding of the 4th ACM Conference on Recommender Systems. New York: ACM, 2010: 293-296.

[5] SHI Y, LARSON M, HANJALIC A. Collaborative filtering beyond the user-item matrix: a survey of the state of the art and future challenges [J]. ACM Computing Surveys, 2014, 47(1): Article No. 3.

[6] 张付志,刘赛，李忠华，等.融合用户评论和环境信息的协同过滤推荐算法[J].小型微型计算机系统,2014, 35(2):228-232.(ZHANG F Z, LIU S, LI Z H, et al. Collaborative filtering recommendation algorithm incorporating user’s reviews and contextual information [J]. Journal of Chinese Computer Systems,2014, 35(2): 228-232.)

[7] WANG B, HUANG J, OU L, et al. A collaborative filtering algorithm fusing user-based, item-based and social networks [C]// Proceedings of the 2015 IEEE International Conference on Big Data. Washington, DC: IEEE Computer Society, 2015: 2337-2343.

[8] JABAKJI A, DAG H. Improving item-based recommendation accuracy with user’s preferences on Apache Mahout [C]// Proceedings of the 2016 IEEE Internetional Conference on Big Data. Piscataway, NJ: IEEE, 2017:1742-1749.

[9] LI S. Collaborative filtering recommendation algorithm based on cloud model clustering of multi-indicators item evaluation [C]// Proceedings of the 2011 International Conference on Business Computing and Global Informatization. Washington, DC: IEEE Computer Society, 2011: 645-648.

[10] KOREN Y, BELL R, VOLINSKY C. Matrix factorization techniques for recommender systems [J]. Computer, 2009, 42(8): 30-37.

[11] 涂丹丹，舒承椿，余海燕.基于联合概率矩阵分解的上下文广告推荐算法[J]. 软件学报，2013,24(3)：454-464.(TU D D, SHU C C, YU H Y. Using unified probabilistic matrix factorization for contextual advertisement recommendation [J]. Journal of Software, 2013, 24(3): 454-464.)

[12] 郭磊,马军,陈竹敏,等.一种结合推荐对象间关联关系的社会化推荐算法[J]. 计算机学报, 2014, 37(1): 219-228.(GUO L, MA J, CHEN Z M, et al. Incorporating item relations for social recommendation [J]. Chinese Journal of Computers, 2014, 37(1): 219-228.)

[13] YANG J, MCAULEY J, LESKOVEC J. Community detection in networks with node attributes [C]// Proceedings of the 2013 IEEE 13th International Conference on Data Mining. Washington, DC: IEEE Computer Society, 2013: 1151-1156.

[14] TANG J, GAO H, HU X, et al. Exploiting homophily effect for trust prediction [C]// Proceedings of the 6th ACM International Conference on Web Search and Data Mining. New York: ACM, 2013: 53-62.

[15] 孟祥武,刘树栋,张玉洁,等.社会化推荐系统研究[J].软件学报, 2015,26(6):1356-1372.(MENG X W, LIU S D, ZHANG Y J, et al. Research on social recommender systems [J]. Journal of Software, 2015, 26(6): 1356-1372.)

[16] YAHYAOUI H, AL-MUTAIRI A. A feature-based trust sequence classification algorithm [J]. Information Science, 2016, 328(C): 455-484.

[17] FANG H, BAO Y, ZHANG J. Leveraging decomposed trust in probabilistic matrix factorization for effective recommendation [C]// Proceedings of the 28th AAAI Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press, 2014: 30-36.

[18] MA H, YANG H, LYU M R, et al. Social recommendation using probailistic matrix factorization [C]// Proceedings of the 17th ACM Conference on Information and Knowledge Management. New York: ACM, 2008: 931-940.

YANGFengrui, born in 1963, Ph. D., professor. His research interests include mobile communication, big data.

ZHENGYunjun, born in 1992, M. S. candidate. His research interests include data mining, recommendation system.

ZHANGChang, born in 1993, M. S. candidate. His research interests include data mining, recommendation system.