基于多层次混合相似度的协同过滤推荐算法

袁正午，陈 然

(重庆邮电大学 计算机科学与技术学院，重庆 400065)

0 引言

随着移动互联网、物联网、云计算等技术的快速发展，全球数据量呈爆炸式增长，大数据时代已经到来。“信息过载”[1]是目前人们所面临的主要问题，所谓的“信息过载”就是社会信息数据量超过了个人或系统所能接受、处理或有效利用的范围，并导致故障的状况。在电商、音乐视频、新闻等领域频发这种问题。

个性化推荐引擎是信息过滤的一种手段，在解决信息过载问题中具有重要的应用与研究价值。个性化推荐系统中最常使用的推荐技术是基于协同过滤的推荐技术，而对于传统协同过滤算法来说，可以分为基于用户的协同过滤算法和基于项目的协同过滤算法[2]，但传统的协同过滤算法也存在一些问题。首先其算法自身就存在数据稀疏性[3]问题，当用户数和项目数急剧增长时，评分矩阵变得极其稀疏，在这种情况下其邻居用户的推荐质量是非常差的；其次算法的相似性度量过于简单，例如余弦相似度、皮尔逊(Pearson)相似性度[4]，这些度量指标都只能描述数据某一方面的相似程度，并不能全面地概括数据之间的相似程度。对此，许多学者提出了自己的解决方案。为了解决数据稀疏情况下推荐精度低的问题，黄创光等[5]提出了一种不确定近邻的协同过滤推荐算法，根据推荐系统应用的实际情况，动态地选择推荐的度量方法来对预测结果进行平衡的推荐。文献[6]在计算用户评分相似度时融合用户人口统计特征产生总体相似度，并引入信任机制，将总体相似度和信任度相结合的混合值作为推荐权重，为用户进行推荐。文献[7]提出了使用奇异值分解(Singular Value Decomposition, SVD)的方法，来对稀疏的用户-物品矩阵进行降维，并挖掘降维后的矩阵与原始矩阵之间的关系，有效解决矩阵信息密度过低的问题。任看看等[8]将Jaccard相似性系数与用户在共同评价项目上的评分差异度相融合，从而获取更加精确的用户相似度矩阵。Al-Shamri等[9]提出了基于模糊权重[10]的相似性的策略，该方法将单一的评分数值模糊化，从一定程度上消除了推荐结果的不准确性。胡伟健等[11]提出了适应用户兴趣变化的改进型协同过滤算法，根据时间转移兴趣变化的特点,改进了相似度的度量方法。贾冬艳等[12]提出了基于双重邻居选取策略的协同过滤推荐算法，以双重指标来确定用户的邻居集合，这种策略提高了邻居集合的准确性，使得推荐更加可靠。王明佳等[13]对项目的特征进行分析，引入项目特征矩阵， 然后结合余弦相似性和基于用户对项目属性偏好相似性综合计算用户的相似性。Polatidis等[14]提出了用户的多分层模型，以一种全新的度量方法来确定用户之间的相似度，提高了用户推荐精度。张南等[15]考虑了用户评分差值、用户全局评分偏好和用户共同评分物品数等三个因素提出了基于改进型启发式相似度模型的协同过滤推荐方法。这些方法在一定程度上提高了推荐的精度，同时也减少了矩阵稀疏性对推荐算法的影响，但没有全面地挖掘用户潜在的相似度，度量方法也存在过于单一和片面的情况。

本文算法主要从改进相似性度量的方法出发，充分挖掘用户之间的潜在的相似度。该方法首先将用户评分模糊化求出用户模糊偏好并结合传统的用户相似度来度量用户相似程度，以此来克服传统协同过滤算法相似度度量的各种缺点；其次不以用户评分相似度作为衡量用户之间相似的唯一标准，而是在此基础上加入了用户兴趣相似度及用户特征相似度，当用户评分较少(数据较为稀疏时)甚至用户公共评分项为空时，该方法通过用户兴趣相似度和用户特征相似度也能一定程度度量用户的相似程度，从而杜绝了用户之间零相似度情况的发生；最后根据用户评分数量来动态地融合用户兴趣相似度和用户特征相似度，使得算法更加灵活多变。总体来说，该算法有效地缓解了数据稀疏性问题和单一度量方法的影响。

1 传统协同过滤算法

传统协同过滤算法首先计算用户或项目之间的相似度，然后选择与目标用户或项目相似度最大的一组用户或项目作为其最近邻居，最后根据这些邻居产生推荐结果。

用户评分数据Rmn用矩阵表示，m表示参与评分的m个用户，n表示评分矩阵中的n个项目，其中Ri,c代表用户i对项目c的评分，用户未评分的项目Ri,c记为0。

计算相似度作为协同过滤算法最核心的部分，传统的主要有3种：余弦相似度、修正的余弦相似度和皮尔逊相似度。

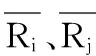
1)余弦相似度。

余弦相似性是一种向量夹角的表示方法，将评分矩阵的每一行看成用户的一个评分向量。

(1)

2)修正的余弦相似度。

修正的余弦相似度，在每个维度减去均值进行修正操作，得到了用户的修正余弦相似性。

(2)

3)皮尔逊相似度。

皮尔逊相似度，主要用于度量两个用户i和j之间的线性相关程度。

(3)

计算完用户之间的相似度，推荐系统会根据目标用户与其他用户之间的相似度按大小排序，选取前L个用户作为目标用户的最近邻居集合。对于用户的最近邻的集合产生预测评分的过程由式(4)给出：

(4)

Pi,c表示用户i对项目c的推荐评分，sim(i,j)表示用户之间的某种相似度，L表示用户以某种相似度选出的用户邻近集合，j表示用户邻近集合中的任意元素。

2 本文相似性度量方法

2.1 改进后的用户评分相似性

在推荐系统中Ri,c表示用户i对项目c的评分，Ri,c的大小体现了用户i对项目c的偏好程度，Ri,c的值越大说明用户i对项目c的偏好程度越大。在现实生活中，大多评价系统要求用户采用数值的形式对项目进行评价，但其不能精确表达用户偏好程度。例如，某电影网站采用5分制评价标准，1分代表最差，5分代表最好，某用户评分为4分，就不能很快地得出用户对该影片的偏好程度，只能从评分出发，大致预测该用户可能很大程度会喜欢该影片，但偏好程度具体为多少就不得而知。在这种情况下，本文将单一的数值丰富化，采用模糊逻辑的方法来表达用户偏好程度。

定义1 设U是一个论域，如果给定了一个映射：μA:U→[0,1],x→μA(x)∈[0,1]，则确定了一个模糊集A，其映射μA称为模糊集A的隶属函数，μA称为x对模糊集A的隶属度。

对评分模糊化，采用图1的定义方法。

μgood(x)=(x-1)/4； 1≤x≤5

(5)

μbad(x)=(5-x)/4； 1≤x≤5

(6)

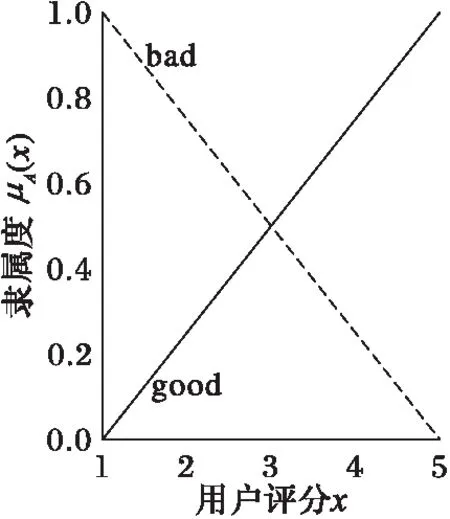
图1 评分三角模糊集隶属函数 Fig. 1 Membership function for score triangular fuzzy set

例如，某用户对一项目的评分为4分，则他对该项目的模糊偏好程度为(0.75,0.25),前者表示用户对该项目的喜爱程度，后者表示用户对该项目不喜好的程度。其模糊偏好程度的计算如下：

μgood=(4-1)/4=0.75

μbad=(5-4)/4=0.25

根据式(5)、(6)，可以得到每个用户的模糊偏好程度；而对于任意的两个用户，他们之间的差异程度往往与每个人的对同一项目的偏好程度息息相关。两用户对同一项目的偏好程度差距越大，即他们之间的评分差异也越大。至此，本文用Ps(i,j)来衡量两个用户i、j对公共项目的平均偏好相似度，可以由式(7)、(8)、(9)得出：

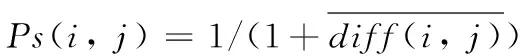
(7)

(8)

(9)

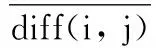
在计算用户评分相似性sima(i,j)的时候，同时结合用户评分的修正余弦相似度和用户评分的Jarccad相似度以此来体现每个用户对项目量纲的平衡和用户之间共同评分项目所占的比例。

sima(i,j)=sim(i,j)adcos×Ps(i,j)×Jaccard(i,j)

(10)

Jaccard(i,j)=|Ii∩Ij|/|Ii∪Ij|

(11)

其中:Ii表示用户i的评分项目集合，Ii∩Ij表示用户i、j共同评论的项目集合，Ii∪Ij表示用户i、j所评论项目集合。

2.2 用户兴趣相似性

在传统的协同过滤推荐算法中，通常没有将用户兴趣相似度考虑在内，但是在现实生活中，用户的兴趣相似度往往对整个推荐系统有着比较重要的作用。例如某个用户他喜欢的影片类型为动作、喜剧，现在有一部电影，它类别可以归为动作、冒险和喜剧等，那么该用户对影片感兴趣的程度很大。这样，可以认为如果两用户i、j的兴趣相似度非常大，j向i进行项目推荐，那么i对推荐的项目感兴趣的程度也很大。基于此推论，定义用户对每类项目的兴趣权重，以此组成用户的兴趣向量。

(12)

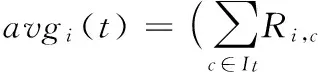
(13)

在式(12)、(13)中，interesti,t表示用户i对类别t的项目的兴趣度，avgi(t)表示用户i对类别t的平均评分，T表示类别集合，Nt表示用户i评论类别为t的项目数量，N表示用户i的所有评分项目数量，α表示兴趣权重，It表示用户i评论类别为t的项目的集合，Ri,c表示用户i对项目c的评分。

例如某用户根据上面的公式可以得到对各类别影片的感兴趣程度，对感兴趣程度进行归一化处理，得到Action、Adventure、Crime、Sci-Fi等兴趣权重分别为24%、15%、12%、15%…，由此，可以看出该用户比较钟情于动作片。至此，可以得出每个用户兴趣向量，而对任意的两个用户i、j来说，其用户的兴趣相似度simb(i,j)可以用式(14)表示：

(14)

其中，interesti,t表示用户i对类别t的项目的兴趣度，T表示类别集合。

2.3 用户特征相似性

人的兴趣爱好很大程度上取决于人的特征属性，其中这些属性包括年龄、性别、 职业、生活的区域位置等。具有不同特征属性的人，其兴趣爱好往往天差地别，例如一个家住城市职业是程序员的年轻男孩与一个家住农村职业是农民的老婆婆，他们之间的兴趣爱好肯定有很大的差别，男孩可能比较热衷于动漫、运动、科技等，但老婆婆可能比较喜欢古典、乡村、健康养生等。因此，本文算法利用这些用户的特征属性，充分挖掘用户之间的隐式相似度。由于年龄、性别、职业、所在区域邮编4个基本特征属性属于比较典型的特征，所以本文采用以上4个特征属性来计算用户的特征相似性。

首先，将用户的特征属性转化成特征向量R(age,sex,work,place)，对于特征属性取值可分为离散的和连续的，对此，作如下定义：用户的年龄取值是连续的整数，所以把用户年龄划分成五个典型的年龄阶段，分别为：1对应0 ～ 18 岁、2对应19 ～ 35 岁、 3对应36 ～ 45岁、 4对应46 ～ 60岁、5对应60岁以上；用户的性别取值是离散的，用m和f对应，m表示用户为男， f表示用户为女；用户的职业取值是离散的，其中取值表示为：occu= {occu1，occu2，…，occun}，其中occun代表具体某个职业；对于所在区域的编码，由于位数多且规律性较强，所以选择编码的前3位数字作为用户的所在的区域。例如某个用户的属性为1|24|M|technician|85711，则该用户所对应特征向量为(2,m,technician,857)。

其次，计算每两个用户之间的相异度。

设用户i、j的特征向量分别为Ri(agei,sexi,worki,placei)，Rj(agej,sexj,workj,placej)。

表1 年龄相异度Tab. 1 Age disparity

(15)

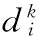
最后，得到用户i、j的特征相似度为：

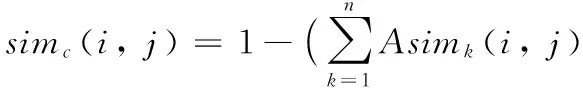
(16)

2.4 用户混合相似性

本文将得到的用户兴趣相似度和用户特征相似度进行动态的融合得到用户类型相似度，其融合因子跟随用户的评分数量变化而变化。当用户的评分数量少于给定阈值d1时，用户兴趣相似度与用户特征相似度的融合因子随用户评论数量的减少而减小。这种情况可以理解为当用户评分数量较少时，用户的兴趣相似度不是很明显，就可以从特征相似度来分别用户，此时降低融合因子即适当减少用户兴趣相似度的权重，同时增加用户的特征相似度的权重来区别用户；当用户评论的数量大于d1同时小于给定阈值d2时,其融合因子稳定在一个特定的值；当用户评论的数量大于d2时；用户此时评论数量较多，只以用户的评分相似度为主来进行推荐。这种策略使得用户之间的相似度呈一种不平衡的分布，随着用户评分数量的增长，用户的邻居集合不固定，确保算法更加灵活。

(17)

其中:count表示用户的评分数量，β为固定的融合因子。

最后将三者融合，得到用户混合相似度：

sim(i,j)=λsima(i,j)+(1-λ)simt(i,j)

(18)

其中:sim(i,j)表示用户i、j的相似度，sima(i,j)表示用户i、j的评分相似度，simt(i,j)表示用户i、j的类型相似度，λ表示平衡因子。

2.5 算法描述

改进后的基于用户的协同过滤推荐算法的具体步骤如下。

输入：用户-项目评分矩阵、项目信息、用户信息、目标用户i、目标项目c;

输出：目标用户i对未评分目标项目c的预测评分。

步骤1 根据用户-项目评分矩阵和式(10)，计算用户的之间的评分相似度sima(i,j)；

步骤2 根据用户-项目评分矩阵、项目信息和式(14)计算用户之间的兴趣相似性，得到用户兴趣相似性simb(i,j)；

步骤3 根据用户特征信息和式(16)计算用户之间的特征相似性，得到用户特征相似性simc(i,j)；

步骤4 根据式(17)，根据用户评论数量动态地融合用户兴趣相似性和用户特征相似性，得到用户类型相似度simt(i,j)；

步骤5 根据式(18)，将用户评分相似度和用户类型相似度进行融合，得到混合的相似性sim(i,j)；

步骤6 通过用户混合相似性大小得到用户i的邻居集L；

步骤7 根据式(4)计算用户i对目标项目c的预测评分Pi,c。

3 实验结果及分析

3.1 实验数据

本文的实验数据采用由明尼苏达州大学在GroupLens研究项目中收集的MovieLens公用数据集，GroupLens站点提供了不同大小的数据集，本文采用ml-100k数据集，该数据集包含943个用户对1 628部电影的100 000个评分，且评分范围为1～5，其数据集的稀疏性为1～100 000/(943×1 682) = 0.936 953，该文件主要存储在u.data中。其中，本文还涉及到两个很重要的文件u.item和u.user：u.item文件描述了这1 683部电影的相关属性，包含电影id、电影名、电影上映时间、电影链接和最重要的电影类别；u.user文件描述了用户的特征属性，包括年龄、性别、 职业、生活的区域邮编等。首先进行数据集的划分，随机地将原有数据分为80%的u.base和20%的u.test，其中u.base用于数据的训练，u.test用于数据的测试。本文算法为多层次混合协同过滤(User Score and Interest and Characteristic Cooperative Filtering, USICCF)推荐算法。

3.2 评价标准

在推荐系统中，有很多不同的评价方式来预测推荐是否成功，本文采用平均绝对偏差(Mean Absolute Error, MAE)作为推荐准确度评价标准。MAE通过计算目标用户的预测评分与实际评分之间的偏差度量预测的准确性，因而MAE指标的值越小，推荐质量越高。假设推荐系统预测项目评分集合为{pre1，pre2，…，pren}，项目实际评分集合为{real1，real2，…，realn}，MAE计算公式如下：

)/n

(19)

3.3 实验结果

实验在基于Scala的IDEA仿真环境下，采用十折交叉验证的方式进行。主要采用MAE评价指标来证明本文所提算法的有效性，首先通过实验确定其未知参数，其次对比分析本文算法和其他几种算法的评价指标。本文取d1=15、d2=150进行下面的实验确定未知参数的取值。

实验一 未知参数的确定。

1)兴趣权重α的确定。

用户兴趣权重主要用于调整用户类别平均分占比和类别数量占比的权重，实验通过改变兴趣权重α和邻居集合数K的取值来观测MAE的变化，其中α的值以0.1为步长从0变化到1，邻居集合数量K以10为步长从10变化到60，USICCF的平均绝对误差MAE如图2所示。

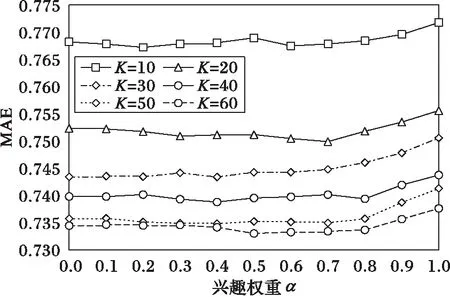
图2 兴趣权重α的确定 Fig. 2 Determination of interest weight α

从图2可以看出，随着邻居数量的增加，当兴趣权重处于0.6左右时，其MAE值最小，至此，本文选取α=0.6。

2)动态融合因子β的确定。

用户类型相似度的动态融合因子主要用于调整用户兴趣相似度和用户特征相似度的权重，确定β的值后，可以根据用户的评论数量动态的确定融合因子。实验通过改变融合因子β和邻居集合数K的取值来观测MAE的变化，其中β的值以0.1为步长从0变化到1，邻居集合数量K以10为步长从10变化到60，USICCF的平均绝对误差MAE如图3所示。

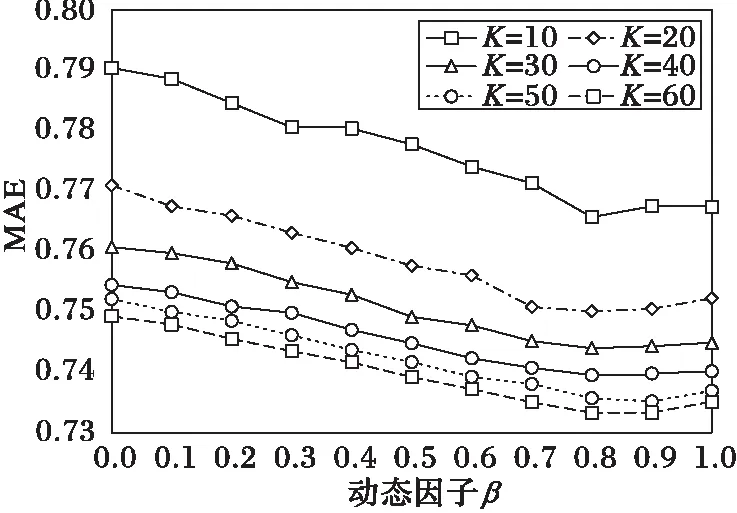
图3 动态融合因子β的确定 Fig. 3 Determination of dynamic fusion factor β

从图3可以看出，当动态融合因子小于0.9左右时，其MAE随融合因子的增加而减少，当动态融合因子大于0.9左右时，其MAE随融合因子的增加而增加，并且可以得出随用户的邻居数逐渐增加，MAE呈下降趋势。至此，本文选取β=0.9。

3)USICCF平衡因子λ的确定。

用户混合相似度平衡因子λ主要调整用户评分相似度和用户类型相似度的权重。实验通过改变融合平衡因子λ和邻居集合数K的值来观测MAE的变化，其中λ的值以0.1为步长从0变化到1，邻居集合数量K以10为步长从10变化到60，混合算法的平均绝对误差MAE如图4所示。

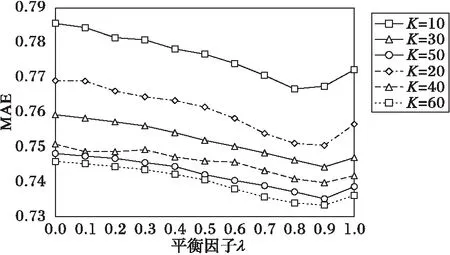
图4 USICCF融合因子λ的确定 Fig. 4 Determination of fusion factor λ of USICCF

从图4可以看出，随着邻居集合数K的增加，相似度平衡因子λ在0.9附近时，MAE的值趋于最小，且前期MAE随平衡因子增加呈递减的趋势，后期随融合因子增加呈递增的趋势。因此本文取λ=0.9进行下面的实验，来对比改进的多层次混合推荐算法与几种协同过滤算法的优劣。

实验二 比较USICCF与几种协同过滤算法的优劣。

本文将改进后的混合推荐算法与几种协同过滤算法进行对比，通过改变邻居集合数K值来比较MAE的变化，邻居集合数量K以10为步长从10变化到100，其平均绝对误差MAE变化结果如图5所示。对比算法如下：

1)CSCF(Cosine-based Similarity Cooperative Filtering)为采用余弦相关系数计算相似性的用户协同过滤算法；

2)ACSCF(Adjusted Cosine-based Similarity Cooperative Filtering)为采用修正余弦相关系数计算相似性的用户协同过滤算法；

3)文献[8]提出的修正的 Jaccard相似性系数的协同过滤(Modified K-pow Jaccard similarity Cooperative Filtering, MKJCF)算法；

4)NUSCF(Native User Score Cooperative Filtering)为只以用户的评分相似性作为唯一评判用户相似度的标准的协同过滤算法。

从图5的实验结果可以看出，随着邻居集合数目的增加，图中5种算法的MAE呈下降趋势，并且随着邻居数目的增加MAE的下降趋势越来越平缓。其中，对于传统协同过滤算法，在前期CSCF算法比ACSCF算法的MAE值要小，但随着邻居数的增加，ACSCF算法MAE值要略小于CSCF算法。MKJCF算法和NUSCF算法，它们的MAE都要小于传统的协同过滤算法，且小于的程度随邻居数量的增加呈递减趋势。随着邻居数目的增加，本文提供的多层次混合推荐算法USICCF的MAE都要小于其他几种算法；尤其在K较小时，其MAE要明显低于其他几种算法：较ACSCF算法来说，在MAE上减少了大约5%；相对于CSCF，在MAE上性能大约提升3%；对于改进后的MKJCF算法，USICCF也存在优势，随着邻居集合数的增加MAE也平均下降了 1%左右；较NUSCF算法来说，USICCF算法也存在略微的优势，随着邻居集合数量的增加，USICCF算法的MAE值都要低于NUSCF算法。最后，本文算法随着邻居数目的增加在MAE上还有逐渐下降的趋势。

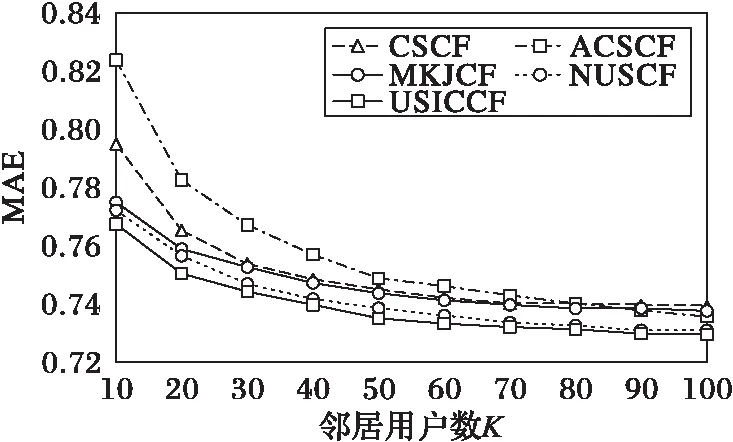
图5 USICCF与几种协同过滤算法的MAE Fig. 5 MAE comparison of USICCF and several cooperative filtering algorithms

4 结语

针对传统协同过滤中的数据稀疏性问题，本文改进得到一种多层次混合相似度的协同过滤推荐算法，该方法在一定程度上减少数据稀疏带来的负面影响，实验结果表明与传统算法相比，尤其在邻居数量较少的情况下，其推荐精度有明显优势，并且比其他几种改进的协同过滤算法的表现也要好。本文方法虽然缓解了算法稀疏性，但算法本身还存在冷启动和拓展性问题，因此需重点研究解决冷启动问题和算法并行化以提高算法的时效。

参考文献(References)

[1] 王娜,任婷.移动社交网站中的信息过载与个性化推荐机制研究[J]. 情报杂志,2015,34(8):190-194.(WANG N, REN T. Information overload and personalized recommendations mechanism in the mobile social networking sites [J]. Journal of Intelligence, 2015,34(8):190-194.)

[2] SAWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms [C]// WWW ’01: Proceedings of the 10th International Conference on World Wide Web. New York: ACM, 2001:285-295.

[3] 孙小华.协同过滤系统的稀疏性与冷启动问题研究[D].杭州:浙江大学,2005.(SUN X H. Research on sparseness and cold start of collaborative filtering system [D]. Hangzhou: Zhejiang University, 2005.)

[4] 冷亚军,陆青,梁昌勇.协同过滤推荐技术综述[J].模式识别与人工智能,2014,27(8):720-734.(LENG Y J, LU Q, LIANG C Y. Survey of recommendation based on collaborative filtering [J]. Pattern Recognition and Artificial Intelligence, 2014, 27(8): 720-734.)

[5] 黄创光,印鉴,汪静，等.不确定近邻的协同过滤推荐算法[J].计算机学报, 2010,33(8):1369-1377.(HUANG C G, YIN J, WANG J, et al. Uncertain neighbors’ collaborative filtering recommendation algorithm [J]. Chinese Journal of Computers, 2010, 33(8): 1369-1377.)

[6] 时念云,葛晓伟,马力.基于用户人口统计特征与信任机制的协同推荐[J]. 计算机工程, 2016,42(6):180-184.(SHI N Y, GE X W, MA L. Collaborative recommendation based on user demographics and trust mechanism [J]. Computer Engineering, 2016, 42(6): 180-184.)

[7] YU K, XU X, ESTER M, et al. Feature weighting and instance selection for collaborative filtering: an information-theoretic approach [J]. Knowledge and Information Systems, 2003, 5(2): 201-224.

[8] 任看看,钱雪忠.协同过滤算法中的用户相似性度量方法研究[J].计算机工程,2015,41(8):18-22.(REN K K, QIAN X Z. Research on user similarity measure method in collaborative filtering algorithm [J]. Computer Engineering, 2015, 41(8): 18-22.)

[9] AL-SHAMRI M Y H, AL-ASHWAL N H. Fuzzy-weighted similarity measures for memory-based collaborative recommender systems [J]. Journal of Intelligent Learning Systems and Applications, 2014, 6(1): 1-10.

[10] 陈雪,黄智力,罗键.基于相对相似度关系的三角模糊数型不确定多属性决策法[J].控制与决策,2016,31(12):2232-2240.(CHEN X, HUANG Z L, LUO J. Approach for triangular fuzzy number-based uncertain multi-attribute decision making based on relative similarity degree relation [J]. Control and Decision, 2016, 31(12): 2232-2240.)

[11] 胡伟健,滕飞,李灵芳.适应用户兴趣变化的改进型协同过滤算法[J]. 计算机应用,2016,36(8):2087-2091.(HU W J, TENG F, LI L F. Improved adaptive collaborative filtering algorithm to change of user interest [J]. Journal of Computer Applications, 2016, 36(8): 2087-2091.)

[12] 贾冬艳,张付志.基于双重邻居选取策略的协同过滤推荐算法[J].计算机研究与发展,2013,50(5):1076-1084.(JIA D Y, ZHANG F Z. A collaborative filtering recommendation algorithm based on double neighbor choosing strategy [J]. Journal of Computer Research and Development, 2013, 50(5): 1076-1084.)

[13] 王明佳,韩景倜.基于用户对项目属性偏好的协同过滤算法[J].计算机工程与应用,2017,53(6):106-110.(WANG M J, HAN J T. Collaborative filtering algorithm based on item attribute preference [J]. Computer Engineering and Applications, 2017, 53(6): 106-110.)

[14] POLATIDIS N, GEORGIADIS C K. A multi-level collaborative filtering method that improves recommendations [J]. Expert Systems with Applications, 2016,48: 100-110.

[15] 张南,林晓勇,史晟辉.基于改进型启发式相似度模型的协同过滤推荐方法[J].计算机应用,2016,36(8):2246-2251.(ZHANG N, LIN X Y, SHI S H. Collaborative filtering recommendation method based on improved heuristic similarity model [J]. Journal of Computer Applications, 2016, 36(8): 2246-2251.)

This work is partially supported by the National Natural Science Foundation of China (61471077), the Program for Changjiang Scholars and Innovative Research Teams in Universities (IRT1299).

YUANZhengwu, born in 1968, Ph. D., professor. His research interests include technology of remote sensing, big data, cloud computing.

CHENRan, born in 1992,M.S. candidate. His research interests include data mining, recommendation algorithm.