基于死区补偿的氧调器平稳切换自抗扰控制
董方酉,孙青林,张晓雷,蒋玉新,孙明玮,陈增强
南开大学 计算机与控制工程学院,天津 300350
供氧系统是歼击机中保证飞行员生命安全的必备设施。其中的氧气调节器(以下简称氧调器)根据飞行员呼吸调节进氧量。随着航空航天技术的发展,新形势对航空供氧装备的要求日趋提高。相比于吸气阻力大,响应速度慢的传统机械式氧调器[1],电子式氧调器系统现在逐渐被广泛应用[2-3]。电子式氧调器的主要控制目的是维持氧气面罩内压强在航空供氧设备国家军用标准1013-90呼吸阻力容许界限[4](以下简称阻力界限)内。由于在歼击机飞行过程中,飞行员的呼吸状态具有很大的随机性和时变性。同时氧调器系统内部执行机构呈非线性特性,尤其驱动阀门具有死区特性,这使氧调器的控制难度很大。因此建立一套符合实际的氧调器系统模型并选择精确的控制策略对于电子氧调器的发展应用具有重要意义。
在国外,法国Air-Liquide公司已将其研制的电控式供氧抗荷调节系统装备在美国F-35战斗机的飞行员防护系统中,具有快速准确的性能。在国内,许多研究仍停留在气动式氧调器的改进和分析中。电子式氧调器的研究相对比较少。孙灿飞[5]和俞笑[2]等采用步进电机作为执行机构,分别采用模糊控制算法来控制氧调器以及对氧调器的单片机硬件设计方案进行了介绍。但步进电机具有体积重量大、能源利用率低和难以实现较高转速等缺点,因此不适用于高标准军用氧调器。李子轩等[3]以直流音圈电机作为氧调器驱动阀,并采用了专家PID控制。Jiang等[6]设计了一套以比例电磁阀为执行机构的电子式氧调器,不可避免地带来了精度低,反应速度慢的缺点。目前,旨在提高氧调器性能的研究和产品也有许多[7-8]。但以上研究中吸气阀门处均无压紧力,容易漏气,大大降低了其应用范围和控制性能。且都没有考虑控制对象含有较大死区的情况。对于死区补偿,文献[9]提出一种模糊PID控制和自适应死区逆补偿串联的死区补偿方法,文献[10]提出了一种基于鲁棒自适应逆的死区补偿方法。但以上所针对的死区问题中,死区相对于模型实际量程较小。针对氧调器中较大死区解决办法的研究则比较少。
氧调器系统阀门执行机构的选择依赖于执行机构的特性。音圈电机具有结构简单、体积小、高速、高加速、响应快等特性,比电磁阀更为精准,对于瞬息万变的歼击机飞行情况,响应更快,适用于氧调器系统。控制策略的选择则依赖于系统的要求。在歼击机飞行中,外界气压、温度的变化、歼击机的飞行状态、以及不同飞行员在不同状态下不同的呼吸频率和强度等因素均影响系统的控制性能。自抗扰控制(ADRC)器是一种针对不确定系统的控制器[11],它可将氧调器系统中的未建模部分、外界的环境变化和飞行员呼吸状态的改变等干扰因素均视为扰动进行观测并补偿。因此适用于氧调器系统的控制。
鉴于现有研究的不足和以上选择分析,为解决阀门漏气问题和实现快速响应、精密控制、强抗扰能力并满足阻力界限的氧调器系统。首先,设计了一套基于音圈电机驱动阀的氧调器系统。在阀门处采用了压紧弹簧,确保在面罩不需进气时音圈电机阀门紧紧关闭,减轻气体泄漏。其次,针对模型强非线性、大死区的特性,设计了基于死区补偿的平稳切换自抗扰控制策略。然后,对自抗扰控制算法通过限幅和死区补偿的改进来解决死区问题的方法进行了详细分析。最后,与仅将死区看作扰动的一般ADRC策略进行比较。通过大量的仿真与对比结果,验证了基于死区补偿的平稳切换ADRC控制策略的高效性、鲁棒性和抗扰性。
1 氧调器系统描述
1.1 工作原理
基于采用压紧弹簧的音圈电机驱动阀的氧调器系统结构示意如图1所示。压差传感器采集腔内气体与大气压的压强差,并转化为电信号传入控制系统,控制系统计算出控制信号,输出至管状线圈,通电线圈在磁场中产生作用力,驱动线圈支撑与铁块做垂直运动,当作用力大于压紧弹簧的密封力时,铁块竖直提起,富氧空气通过。其特点在于:在铁块上方引入压紧弹簧,固定于图中所示位置,用以压紧阀门。当驱动阀门无输入信号或由于扰动输入小信号时,由于压紧弹簧时刻处于压缩状态,压紧力使阀门不会轻易打开。吸气时,面罩内压强低于外界压强,音圈电机驱动阀门打开,从而吸入气体;呼气时,面罩内压强高于外界压强,面罩腔呼气阀门打开,从而呼出气体。将面罩内压强差作为控制对象,使其在各个呼吸频率下满足阻力界限如表1所示。
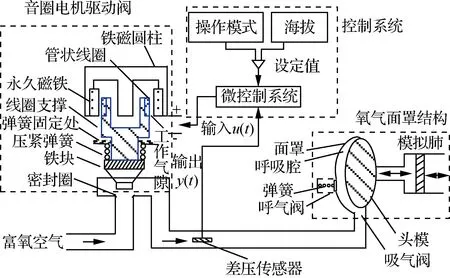
图1 氧调器系统结构示意图Fig.1 Schematic diagram of oxygen regulator system

表1 理想呼吸阻力界限Table 1 Ideal respiratory resistance boundaries
1.2 基于音圈电机驱动阀的氧调器系统模型
在模型建立时进行理想性假设:假设气体为理想气体;模型中各静态参数为常值;面罩内压强与肺部压强均匀分布;气体回路中的温度保持不变。
1.2.1 带压紧弹簧的音圈电机驱动阀模型
音圈电机是一种特殊形式的直接驱动电机。其工作原理是,通电线圈(导体)在磁场内会产生力,力的大小与施加在线圈上的电流成比例[12]。文献[13]详细介绍了音圈电机的磁学原理、电子学原理以及机械系统原理;文献[12]对音圈电机进行了简化建模。
通常在研究中,氧调器所用驱动阀门的执行机构均具有一定的死区,但死区较小,可近似忽略。但一般军用氧调器阀门皆具有压紧策略。因而本文采用具有压紧阀门作用的弹簧安装在铁块与线圈支撑中间,与音圈电机安培力形成对抗力,从而使阀门不会由于扰动而轻易打开。因而,驱动阀模型可表示为
(1)
式中:x为阀门位移;kt为用于压紧阀门弹簧的弹性系数;Fs为实际情况中阀门运动中受到的摩擦力和弹簧预压紧力的和;ktx+Fs即除音圈电机本身外的非线性因素,也是死区的主要来源。式(1)的其他参数说明见文献[12]。由于在实际运行中,电感L很小,可以忽略其影响。这样,消去中间变量可得阀门位移与控制电压u之间的关系为
(2)
流过阀门的流量与阀门位移的关系为[14]
(3)
式中:K为阀门的超临界常量,可以通过式(4)计算得到;μ为流量系数;π=3.14;d为阀门直径;x(t)为阀门位移;P0为阀门入口处的气体压强;T为随时间变化的阀门入口处的气体温度。
(4)
式中:k0为气体绝热指数;R0为气体常数;g为重力加速度。
另外,为了研究阀门特性,在实际设备中,将输入电压以0.5 V为步长从0 V递增至12 V,采用位移传感器采集阀门位移数据并记录下来。作得输入电压与阀门位移的关系如图2所示。从图中看出,输入电压与阀门位移呈非线性关系,具有死区特性。s代表实验测得的死区大小,由数据估得为6 V。由图知,在控制量小于6 V时,由于弹簧的预压紧作用,阀门无法打开。相比于阀门的实际使用范围(6~8 V),死区(0~6 V)非常大,增加了控制难度。如何有效跳出死区同时又不引起震荡是控制策略着重解决的问题。
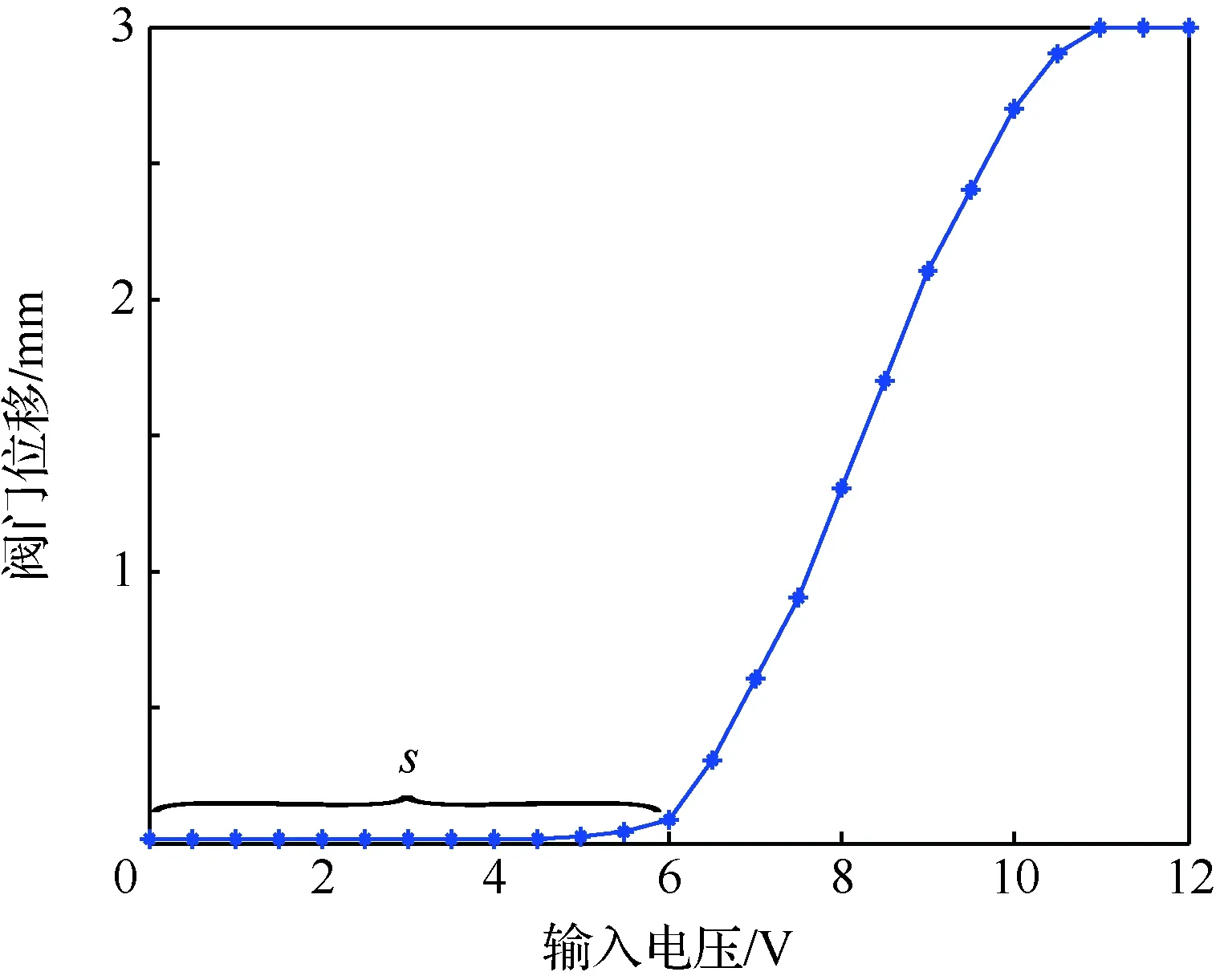
图2 输入电压与阀门位移的关系Fig.2 Relationship between displacement of valve and input voltage
1.2.2 呼吸模型
人体呼吸具有一定规律[15]。飞行员在不同飞行环境下的肺通气量情况在文献[16]中有所介绍,其呼吸呈正弦规律变化,呼吸频率各情况下不同,具有时变特性,采用的数学模型为
(5)
式中:Gr(t)为呼吸质量流量,单位为kg/s;Vi为潮气量,即每次呼吸的肺通气量,单位为L/cycle;n为呼吸频率,单位为cycles/min。
1.2.3 呼气阀模型
当面罩内气体压强大于外界压强时,呼气阀弹簧压缩,呼气阀门打开,气体流出。其数学模型为
(6)
(7)
式中:Ge为质量流量;Bn为亚临界流量常量;Bs为超临界流量常量;de为呼气阀直径;Ke为弹簧刚度;Le0为弹簧预压缩量;Le(t)为阀门开度;P(t)为呼吸腔内压强;Pa为基准压腔压强;吸气时,Ge(t)=0, 呼气阀门闭合。
1.2.4 呼吸腔模型
腔内气体实为氧气,这里假设为理想气体,因此满足理想气体状态方程:
P(t)V(t)=M(t)R0T
(8)
那么,呼吸腔内的压力动态方程为
(9)
(10)
式中:G(t)、Gr(t)和Ge(P(t),t)分别为音圈电机驱动阀的质量流量、呼吸质量流量和呼气阀质量流量;V(t)和M(t)分别为呼吸腔内气体体积和质量。因此,被控对象的输出为
y(t)=P(t)-Pa
(11)
1.2.5 系统动态方程
联合式(2)~式(11)可得到基于音圈电机驱动阀的氧调器系统模型。若令

(12)
2 控制策略
2.1 自抗扰控制原理
20世纪90年代,韩京清教授提出了自抗扰控制理论。自抗扰控制器的典型结构包括3部分:扩张状态观测器(ESO)、跟踪微分器(TD)和非线性状态误差反馈(NSEF)[17]。它继承了PID不依赖于被控对象数学模型的优点,将未建模误差和系统外界扰动,通过扩张状态观测器观测出来,进行补偿,使其变为串联积分型,从而实现主动抑制扰动。针对某些建模不完全,受外扰影响严重的系统控制取得了良好效果。但其参数众多不便整定,克利夫兰大学的高志强教授提出了线性自抗扰控制(LADRC)理论[18],用带宽概念简化了参数的调整。其原理如图3所示。近年来, ADRC以其良好的控制效果, 在多个领域得到了推广应用[19-22]。
一般二阶被控对象可写为
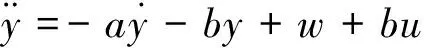
(13)
式中:y为系统输出;u为系统输入;w为系统外部扰动;a、b为系统参数。式(13)最终可写为
(14)
式中:b0为b的估计值;f相当于系统的总扰动。因此可得系统状态方程为
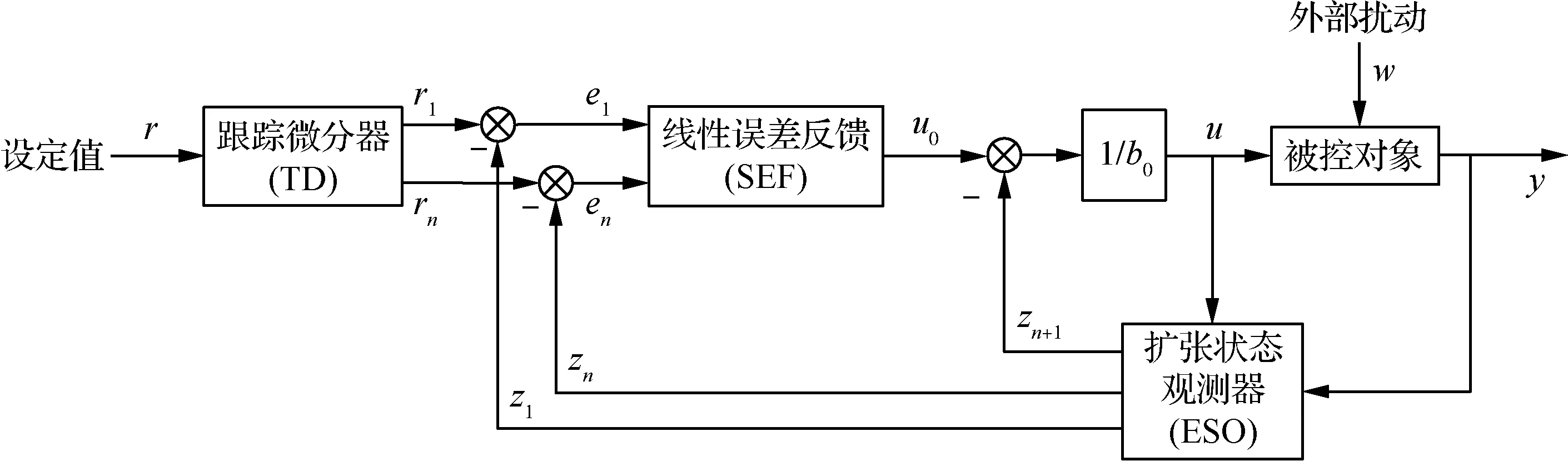
图3 自抗扰控制原理图Fig.3 Schematic diagram of ADRC
(15)
其扩张状态空间形式为
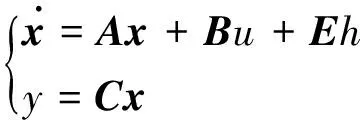
(16)
式中:
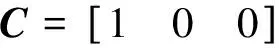
系统的总扰动f可以通过线性扩张状态观测器(LESO)观测出来,如式(17)所示:
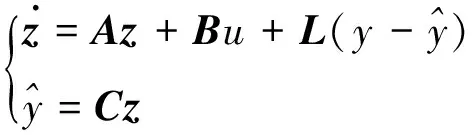
(17)
从而根据线性观测器的理论可得
(18)
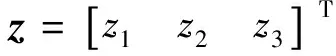
u0=kp(r-z1)-kdz2
(19)
u=(u0-z3)/b0
(20)
式中:kp、kd为控制器参数;r为设定值。至此,可得到自抗扰算法的控制量u。
2.2 针对模型特性的控制优化
本文所述的氧调器系统具有大死区、非线性、时变、易受扰动影响等特点。针对以上特性,采用基于死区补偿的平稳切换ADRC策略如图4所示。在采用自抗扰算法之外,采用开环闭环结合的控制方式,即图4中的分段。但是,在开环闭环的切换处容易引起震荡。代表切换点的分界值也需要经过大量仿真试凑得出一个最佳值e0。为保证控制量平稳切换,采取两个限幅环节,其中第1个限幅为Min1到Max1,第2个限幅为Min2到Max2。同时通过1.2.1节中实验测得的阀门输入输出数据分析预估死区大小,计算出相应控制量大小q加入到控制量中以补偿死区。下面分别介绍了本文采取的针对模型非线性的改进控制方法。
1)死区预估补偿
由于音圈电机驱动阀处压紧弹簧的作用,控制量在一定范围内时阀门无法打开,形成死区。不变性原理[23]指出:实际的控制系统都会受到外部扰动的影响。如果这种扰动能够被测量出来,就有可能利用它来产生控制作用,以消除其对输出的影响。此处可将死区作为可以测得的扰动来处理。因此采用测试阀门输入输出关系的实验来预估出死区的大小s,从而得出可以跳出死区的控制量q。可通过死区补偿来快速跳出死区进入线性区。
2)不同阶段平稳切换
由于吸气时需要调节阀门开度保证适度进气,呼气时则需要迅速关闭阀门保证不再进气。
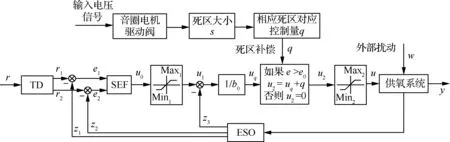
图4 基于死区补偿的平稳切换自抗扰控制策略图Fig.4 Schematic diagram of smooth-switching ADRC strategy based on dead zone compensation
因此,在吸气阶段采用闭环控制。在呼气阶段,直接将控制量设置为常值(此策略中为0),此常值保证阀门关闭,即采用开环控制。但由于控制量频繁切换极易引起系统震荡、失稳和控制量超出所需范围或超出硬件量程。而限幅不仅代表着实际物理设备的能力限制,也体现了控制系统一些特定的考虑因素[24]。因此本文采用双限幅,即分别在两个不同部位引入饱和模块,以达到控制量平稳切换的效果。
1)由于加入死区补偿后影响了ADRC控制量的范围,造成ADRC控制量未在理想阈值内,且其阈值并不固定。这直接影响了控制性能,因而对ADRC控制量的限幅十分必要。因此,在ADRC计算之后,死区补偿之前进行ADRC控制量的限幅。引入饱和限幅函数sat(·),限制上下幅,分别如式(21)和式(22)所示:
(21)
式中:Max1为ADRC计算出的控制量所允许的最大值;u0(t)为ADRC计算出的控制量。
(22)
式中:Min1为ADRC计算的控制量所允许的最小值。通过式(21)和式(22)同时限制上下幅。限幅函数sat(·)的定义为

(23)
2)由于控制信号为电压信号,根据执行机构的应用特性,为了避免系统输出饱和,限幅方式选取:
(24)
式中:u2(t)为系统限幅之前的控制量(u2≥Min2,Min2=0),Max2为系统允许的最大控制量,其取值与硬件系统所能允许的最大电压对应。
2.3 控制器设计
式(12)给出的系统状态方程可分离为
(25)
同时可表示为
(26)
式中:f1(u)为含有控制量u的表达式;f2(·)为其他部分表达式。由文献[25]可知,n阶系统的自抗扰控制器可有多种选择。这里,式(25)可以改写为
(27)
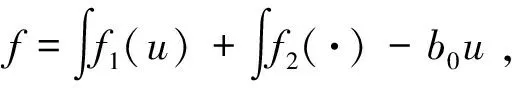
3 仿真分析
本节将把死区当作扰动的一般ADRC控制方法与本文提出的基于模型非线性改进的ADRC控制方法进行对比分析,仿真对比验证了所提出控制策略的高效性。 之后的综合对比则分别说明了死区补偿和双限幅的必要性。
3.1 仿真条件
本实验通过MATLAB仿真来实现。仿真步长设置为固定步长0.001 s;仿真时间为12 s;呼吸频率依次设置为20、30、45次每分钟。模型参数如表2所示。
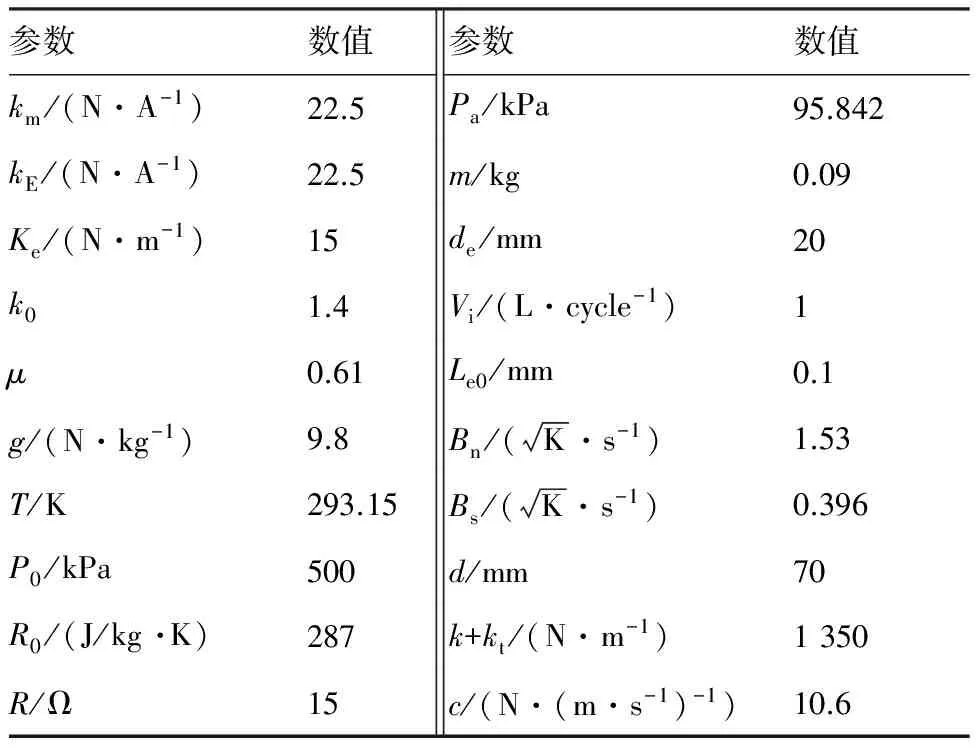
表2 氧调器系统参数Table 2 Parameters of oxygen regulator system
1)e0的选取
e=0-P(t)为面罩压差和跟踪目标0之间的误差信号。误差信号是否大于0表示面罩内压强差是否小于0,可以直观判断出系统处于吸气还是呼气状态。而开闭环分界值e0的取值则因不同控制策略而不同,需由反复调试和试凑得出。按照最终控制策略,e0取为-0.016 kPa。
2)q的选取
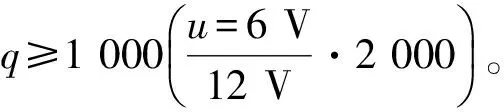
3)Max1、Min1、Max2和Min2的选取
Max1、Min1是第1个限幅环节的上下幅,表示对ADRC控制量的直接限制。从大量仿真数据分析得出,最终有效控制量为1 200~1 400。而由于加入了大约1 000的前馈补偿量,因此,此限制取为200~400(无单位)。Max2、Min2是第2个限幅环节的上下幅,表示对最终控制量的限制,由执行机构允许值而定。占空比应保证在0到1之间,因此上下幅分别取值为2 000和0。
文中应注意:图中的面罩压力指面罩内压强与基准压腔内压强的压强差。
3.2 ADRC控制
ADRC具有主动抑制扰动的特点,首先采用将死区当作扰动的一般ADRC策略。控制器参数为:w0=360,b0=11.8,kp=8 820,kd=165。当呼吸频率为30次/min时,结果如图5所示,初始吸气阶段面罩压强存在较大负向尖峰值,控制量存在超调。存在超调的原因是,当呼气结束开始吸气时,由于死区的存在并且死区较大,此时的控制量需要增长到一定值才能将吸气阀门打开,因此在阀门未打开这段时间内,面罩内处于漏气状态,压强值极具下降,随着控制量增大到足够打开阀门时,才逐渐开始吸气,气压回升。因此,从面罩内压强显示来看,就呈现出一个负向尖峰值。往往参数w0越大,ESO对扰动的估计能力越强。此情况下,尽管w0已经调至很大,死区却仍然无法通过ESO估计出来并抵消。因此,仅仅依靠参数调节无法解决超调的问题。
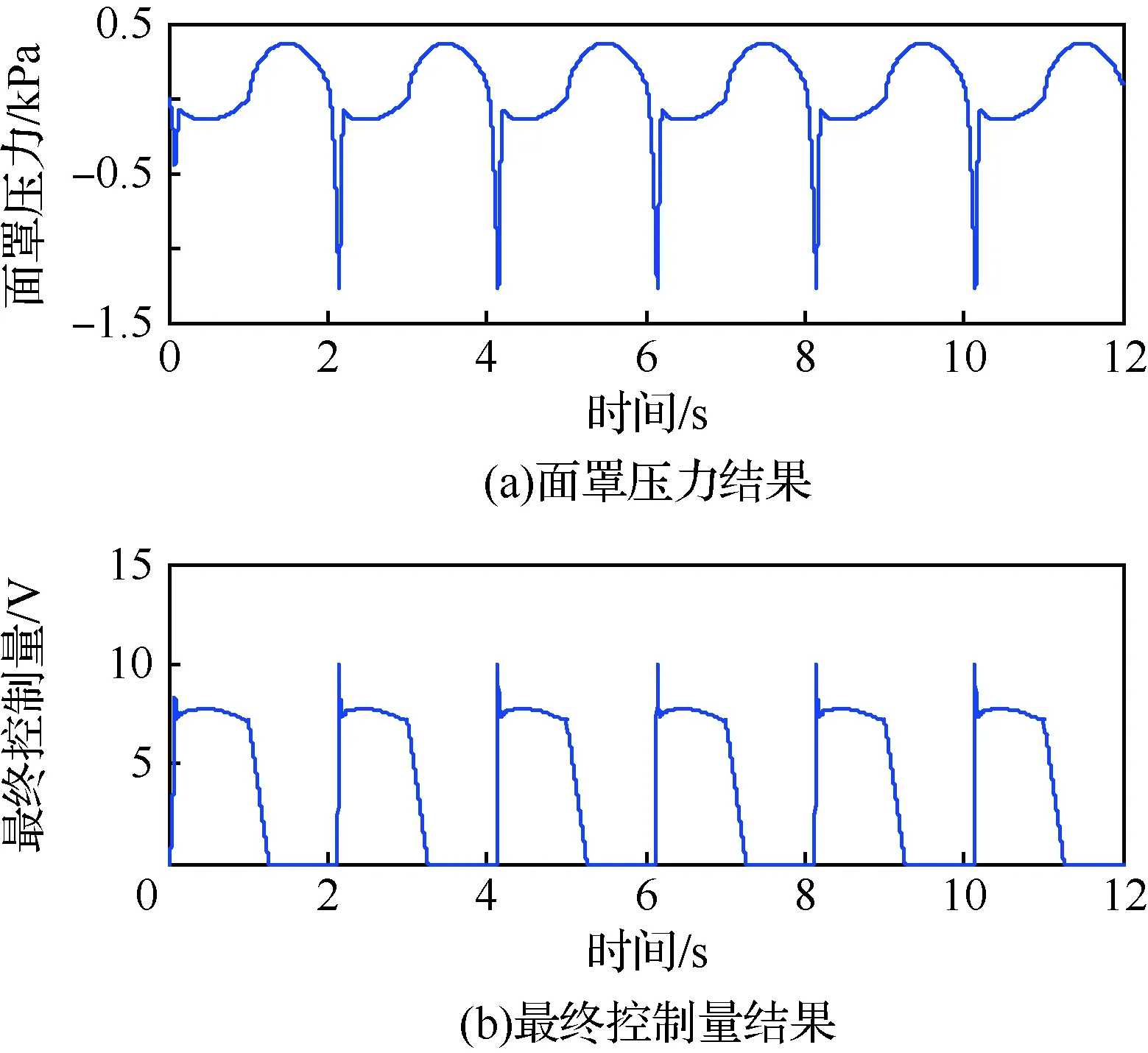
图5 呼吸频率为30次/min时的ADRC结果Fig.5 Results of ADRC with 30 times/min respiratory rate
3.3 针对模型非线性的改进ADRC控制
针对本模型中的非线性环节,采用死区补偿模块和两个饱和模块,即本文提出的基于死区补偿的平稳切换ADRC控制策略(原理已在第2节中描述),控制参数为:w0=360,b0=11.8,kp=8 820,kd=165,e0=-0.016,q=1 000。呼吸频率为20、30、45次/min时的结果分别如图6所示。可知,吸气阻力限制在0.15 kPa,呼气阻力限制在0.27 kPa。经仿真验证,本策略及参数是既能保证控制量在合理范围内又能保证其在切换时不引起震荡的最佳方案。由图可看出,采用双层限幅方法后,既去除了超调和震荡,达到了平稳切换的目的,解决了严重的死区问题。同时能保证面罩内压强在各个频率时均在阻力界限之内。
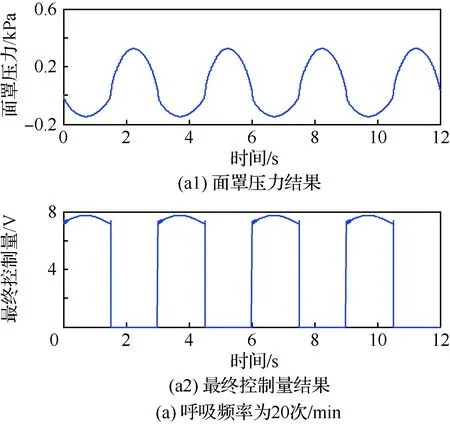
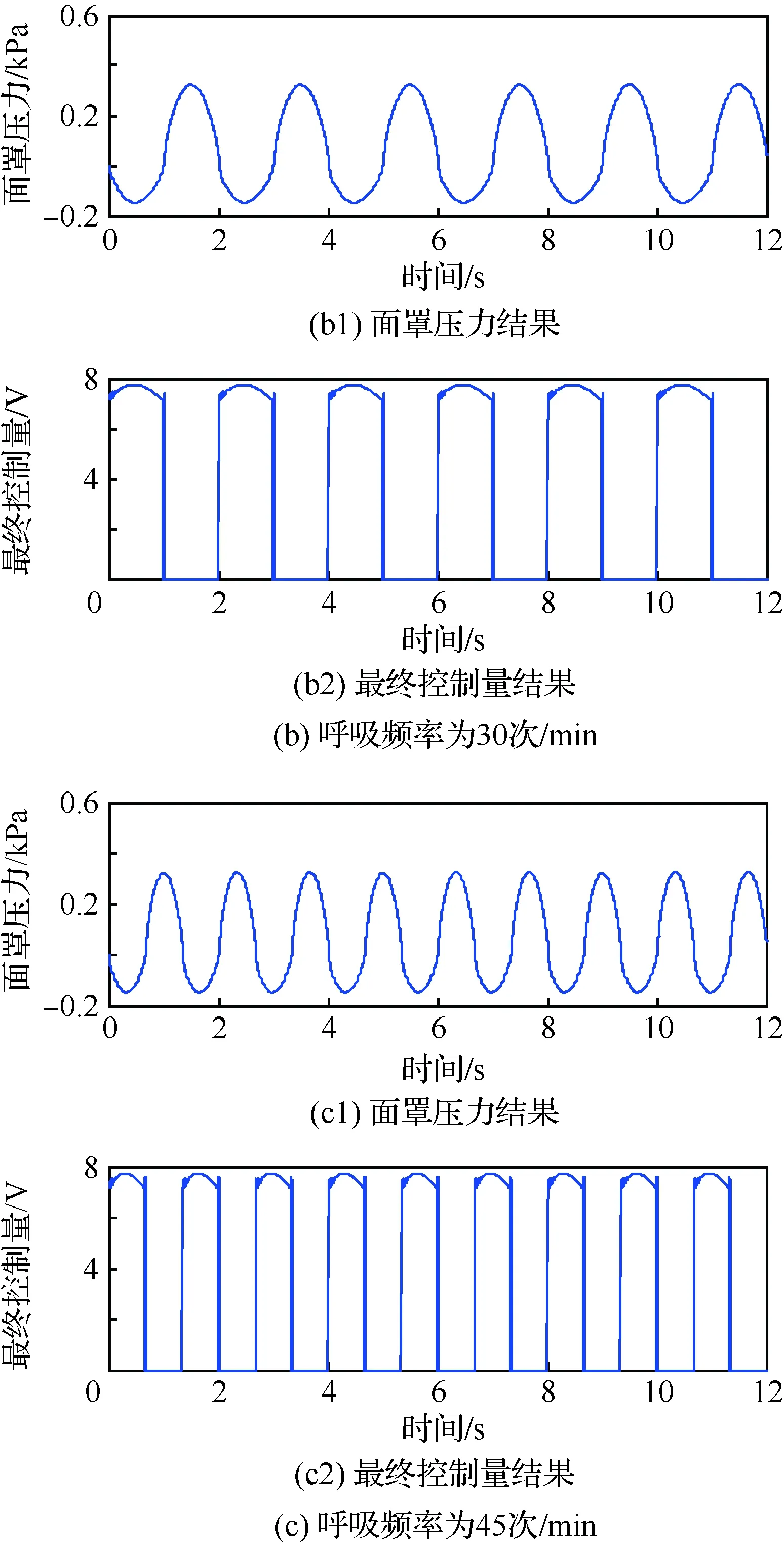
图6 不同呼吸频率时的改进的ADRC结果Fig.6 Results of improved ADRC with different respiratory rate
3.4 鲁棒性与抗扰性验证
为验证系统的鲁棒性,将模型中死区大小s进行 10%左右的改变,即分别为s-1,s,s+1,且控制器参数保持不变时,在呼吸频率为45次/min的面罩压强变化如图7所示。由图可知,在死区变为s-1,s+1时,虽然分别略微震荡和超调,但面罩内压力仍能保证在阻力界限内。证明了在一定死区变化范围内,该控制策略及同一套控制参数具有鲁棒性。
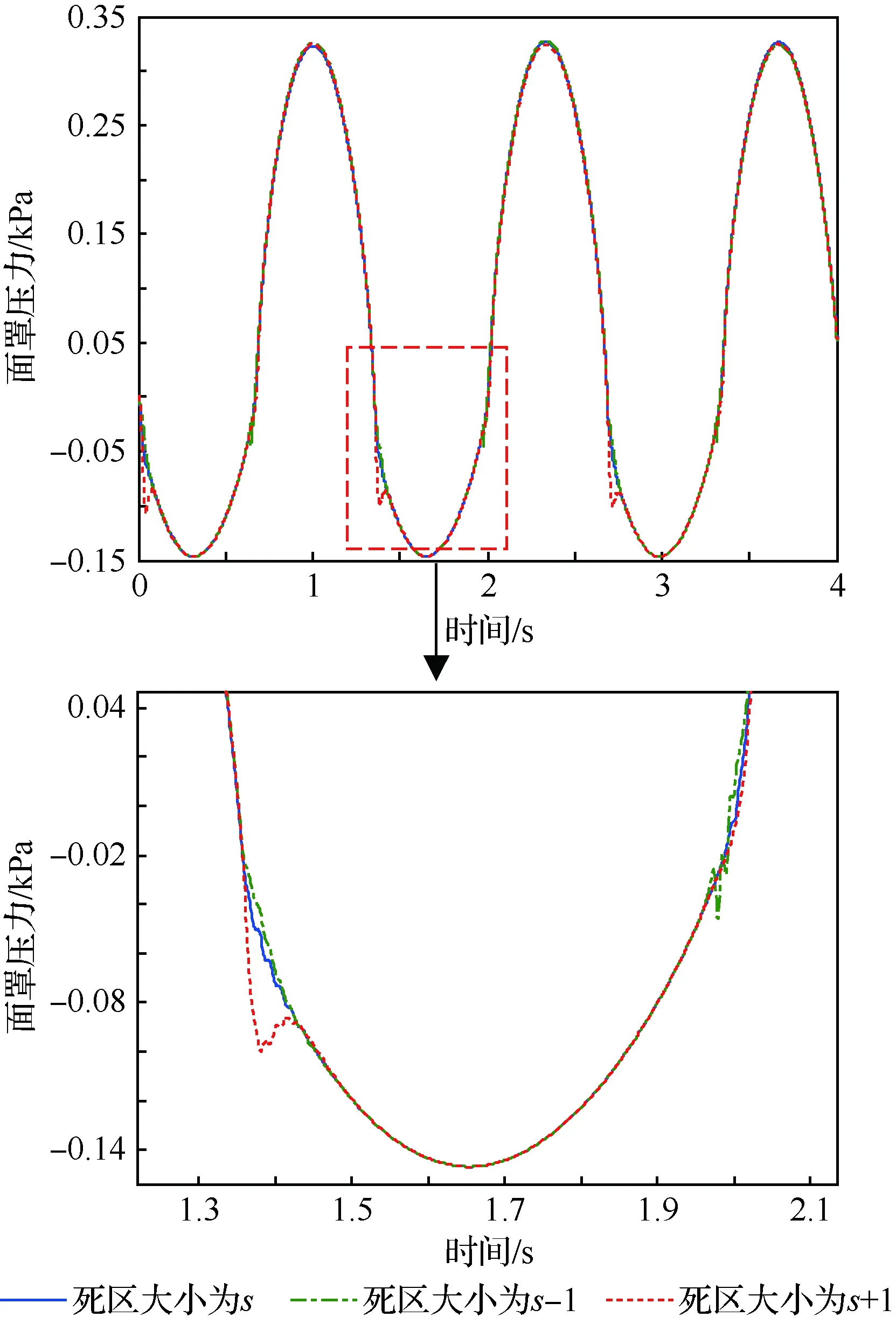
图7 不同死区的改进的ADRC结果Fig.7 Results of improved ADRC for different dead zones
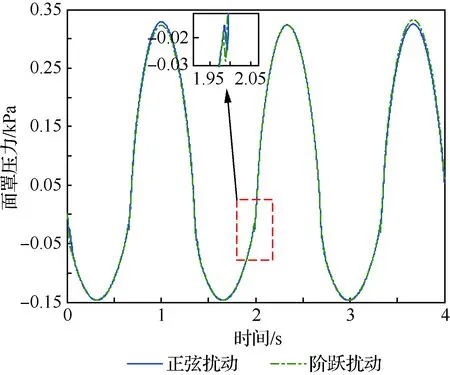
图8 不同扰动的结果Fig.8 Results of different disturbance
为验证系统的抗扰性,分别输入幅值为1的正弦信号模拟人体加深呼吸,以及幅值为1 的阶跃信号模拟人体咳嗽。呼吸频率为45次/min时面罩内压强变化如图8所示。由图可知,在扰动作用下,虽然略微震荡,但仍保证在阻力界限内。证明了控制系统的抗扰能力。控制系统的抗扰性和鲁棒性得益于自抗扰良好的抗干扰能力和本文所采用的改进方法。
3.5 仿真对比
为了说明针对模型改进的死区补偿与双限幅的必要性。这里,采用相同的ADRC控制参数,将ADRC控制(ADRC)、仅补偿死区却单限幅的ADRC控制(死区补偿ADRC)以及本文所采用死区补偿和双限幅的ADRC控制(改进的ADRC)在呼吸频率为45次/min时作综合对比如图9所示。前两者均存在超调。这是死区所造成的现象。震荡则是静态死区补偿和控制切换所造成。而本文提出的基于死区补偿的平稳切换ADRC控制则解决了这两个问题,实现了无超调和平稳切换。3种控制方法对比总结如表3所示。
本文提出的控制策略对死区问题的解决和提高含有死区非线性特性的氧调器的控制性能具有重要意义。而且该策略采用相同的控制参数在不同的呼吸频率下均能达标,且具有鲁棒性和抗扰性。这对氧调器的批量生产与广泛应用具有一定价值。
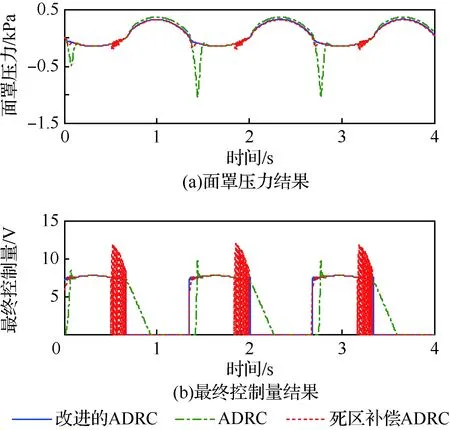
图9 3种方法对比结果Fig.9 Comparison results of three methods

表3 3种方法对比Table 3 Comparison of three methods
4 结 论
1) 基于现实情况,在氧调器系统中采用压紧弹簧以改善漏气状况。建立了基于音圈电机驱动阀的氧调器系统模型。并运用自抗扰控制算法进行控制。
2) 针对模型死区特性,提出了一种解决含有较大死区问题的方法:首先,通过实验测得实际机构中主要的死区大小,采取静态死区补偿量予以补偿;然后,采用双层限幅以避免超调和震荡。最后,其他未建模部分和未考虑到的死区因素利用自抗扰算法主动抑制扰动的特点来解决。
3) 分别对ADRC、死区补偿ADRC和改进的ADRC进行仿真对比,说明了死区补偿和双限幅的必要性和有效性。采用基于死区补偿的平稳切换ADRC控制方法优于其他方法,呼吸阻力更低。
4) 提出了一整套氧调器系统的模型和控制方法,并将面罩内压强控制在阻力界限内。模型更接近真实情况,控制方法更精确。同一套控制参数可在各呼吸频率下满足要求,具有鲁棒性和抗扰性。
参 考 文 献
[1] 肖华军. 航空供氧装备生理研究回顾与展望[J]. 航空学报, 2001, 22(5): 441-443.
XIAO H J. Review and expectation on the physiological research about the aviation oxygen equipment[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(5): 441-443 (in Chinese).
[2] 俞笑, 孙兵, 林贵平,等. ATmega128单片机在电子式氧气调节器上的应用[J]. 网络新媒体技术, 2009, 30(12): 50-56.
YU X, SUN B, LIN G P, et al. ATmega128 singlechip using on aircraft electronic oxygen regulator[J]. Microcomputer Applications, 2009, 30(12): 50-56 (in Chinese).
[3] 李子轩, 林贵平, 曾宇, 等. 基于LabVIEW的电子式氧调器PID控制系统的设计[J]. 计算机测量与控制, 2016, 24(3): 80-83.
LI Z X, LIN G P, ZENG Y, et al. Control system designed for electronic oxygen regulator based on LabVIEW[J]. Computer Measurement and Control, 2016, 24(3): 80-83 (in Chinese).
[4] 中国航空综合技术研究所. 航空供养装备呼吸阻力容许界限: GJB 1013-90[S]. 北京:中国航空综合技术研究所, 1990.
China Aero Polytechnology Establishment. Acceptable levels for breathing resistance of aircraft oxygen equipment: GJB 1013-90[S]. Beijing: China Aero Polytechnology Establishment, 1990 (in Chinese).
[5] 孙灿飞, 蔡元友, 龙海军. 电子式氧气调节器中步进电机模糊控制技术研究[J]. 测控技术, 2013, 32(4): 78-81.
SUN C F, CAI Y Y, LONG H J. Research on stepping motor fuzzy control technology application in the aircraft electronic oxygen regulator[J]. Measurement and Control Technology, 2013, 32(4): 78-81 (in Chinese).
[6] JIANG Y X, SUN Q L, ZHANG X L, et al. Pressure regulation for oxygen mask based on active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2017, PP(99): 1-9.
[7] ZENG Y, DU C H, ZHOU Y, et al. Design of electronic aviation oxygen regulator structure[J]. Applied Mechanics & Materials, 2013, 421(1): 150-156.
[8] JIANG Y X, SUN Q L, CHEN Z Q, et al. Modeling and simulation of an electronic oxygen regulator based on generalized predictive control algorithm[C]∥34th China Control Conference(CCC). Piscataway, NJ: IEEE Press, 2015: 4067-4072.
[9] 李妍, 毛志忠, 王福利, 等. 电弧炉电极调节系统的自适应死区补偿控制[J]. 控制与决策, 2010, 25(10): 1474-1478.
LI Y, MAO Z Z, WANG F L, et al. Adaptive deadzone compensation control of electrode regulating system of electric arc furnace[J]. Control and Decision, 2010, 25(10): 1474-1478 (in Chinese).
[10] WANG Z H, YANG B, CHENG L, et al. Robust adaptive dead-zone compensation of DC servo system[J]. IEE Proceedings Control Theory and Applications, 2006, 153(6): 709-713.
[11] 陈增强, 程赟, 孙明玮, 等. 线性自抗扰控制理论及工程应用的若干进展[J]. 信息与控制, 2017, 46(3): 257-266.
CHEN Z Q, CHENG Y, SUN M W, et al. Surveys on theory and engineering applications for linear active disturbance rejection control[J]. Information and Control, 2017, 46(3): 257-266 (in Chinese).
[12] 兴连国, 周惠兴, 侯书林, 等. 音圈电机研究及应用综述[J]. 微电机, 2011, 44(8): 82-87.
XING L G, ZHOU H X, HOU S L, et al. Research and application of voice coil motor[J]. Micromotors, 2011, 44(8): 82-87 (in Chinese).
[13] 张大卫, 冯晓梅. 音圈电机的技术原理[J]. 中北大学学报(自然科学版), 2006, 27(3): 224-228.
ZHANG D W, FENG X M. The technical principle of voice-coil actuator[J]. Journal of North University of China (Natural Science Edition), 2006, 27(3): 224-228 (in Chinese).
[14] WHITE F M. Fluid mechanics[M]. 7th ed. New York: McGraw-Hill, 2011: 154-163.
[15] BEAUMONT M, LEJEUNE D, ISABEY D, et al. Positive pressure generation by pneumatic and electronic O2 regulators: a bench experimental evaluation[J]. Aviation Space and Environmental Medicine, 1999, 70(8): 812-816.
[16] 中国航空综合技术研究所. 飞行员飞行中肺通气参数: GJB 305-87[S]. 北京: 中国航空综合技术研究所, 1987.
China Aero Polytechnology Establishment. Pilot’s parameters of pulmonary ventilation during flight: GJB 305-87[S]. Beijing: China Aero Polytechnology Establishment, 1987 (in Chinese).
[17] HAN J Q. From PID to active disturbance rejection control[J]. Industrial Electronics IEEE Transactions, 2009, 56(3): 900-906.
[18] GAO Z Q, Scaling and bandwidth-parameterization based controller tuning[C]∥American Control Conference. Piscataway, NJ: IEEE Press, 2003, 4989-4996.
[19] 吴超, 王浩文, 张玉文, 等. 基于LADRC的无人直升机轨迹跟踪[J]. 航空学报, 2015, 36(2): 473-483.
WU C, WANG H W, ZHANG Y W, et al. LADRC-based trajectory tracking for unmanned helicopter[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 473-483 (in Chinese).
[20] 李自行, 李高风. 移动质心再入飞行器建模及自抗扰滚动控制[J]. 航空学报, 2012, 33(11): 2121-2129.
LI Z X, LI G F. Moving centroid reentry vehicle modeling and active disturbance rejection roll control[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2121-2129 (in Chinese).
[21] ZHENG Q, GAO L Q, GAO Z. On validation of extend ed state observer through analysis and experimentation[J]. Journal of Dynamic Systems Measurement and Control, 2012, 134(2): 024505-1-11.
[22] XIA Y Q, PU F, LI S F, et al. Lateral path tracking control of autonomous land vehicle based on ADRC and differential flatness[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3091-3099.
[23] 刘善慧, 梅雪松, 李健, 等. 多色套准系统前馈自抗扰控制器设计[J]. 机械工程学报, 2015, 51(5): 143-150.
LIU S H, MEI X S, LI J, et al. Design feed-forward active disturbance rejection control controller for multi-color register system[J]. Journal of Mechanical Engineering, 2015, 51(5): 143-150 (in Chinese).
[24] 薛安成, 耿继瑜, 刘瑞煌,等. 限幅环节对DFIG故障中输出特性的影响研究[J]. 电力自动化设备, 2017,37(10): 29-32.
XUE A C, GENG J Y, LIU R H, et al. Impact of limiter on output characteristics of DFIG during fault[J]. Electric Power Automation Equipment, 2017,37(10): 29-32 (in Chinese).
[25] 张超, 朱纪洪, 高亚奎. 自抗扰控制器的阶次与参数的选取[J]. 控制理论与应用, 2014, 31(11): 1480-1485.
ZHANG C, ZHU J H, GAO Y K. Order and parameter selections for active disturbance rejection controller[J]. Control Theory and Applications, 2014, 31(11): 1480-1485 (in Chinese).

