空炸点声学测量系统设计及关键技术研究
李大伟,刘云海,万博,周磊,王婷
(中国白城兵器试验中心吉林白城137001)
各类远程压制、防空反导、精确制导等武器弹药试验鉴定中,空炸点或开舱点测量是检验武器弹药性能的一项重要特征参数,传统试验中主要应用光学[1-2]设备进行直接测量,但在一些弹道偏差大、目标特性弱、落弹区地形复杂等情况下,传统测试设备存在着一定局限性。
鉴于弹药战斗部空炸或开舱时会产生特有的声信号,这为利用声探测技术进行参数测量提供了可能。迄今为止,美国、俄罗斯、英国、以色列和日本等国均装备有成熟的被动声探测系统,如以色列菲尔公司的AEWS声探测预警系统、瑞典的Helisearch直升机声测系统[3]。在国内外,声探测技术广泛应用于直升机探测、智能雷弹,近年来应用于单兵声测系统[4]及反狙击手系统[5-7]等领域。
1 系统总体方案设计
常规靶场中,声测作为一种新兴测试技术,具有独特优势。首先,战斗部空炸或开舱时会产生一种特有的声波,无需在弹药上加装光、电等合作装置,借助这种特有声波可进行声测设备的触发数据记录,便于系统无人值守、抵近测量。其次,声学传感器体积小、重量轻、造价低、技术相对成熟,便于构建声学阵列实现矢量测量。另外,声测设备运输便捷、布站简易、场地适应性强,数据处理快速,具备准实时结果显示能力,便于现场数据分析和方案适时调整,提高试验效率。
1.1 系统架构及结构组成
本系统总体上由3个分站(即检靶仪)和一个中心站(即数传仪)组成,如图1所示。

图1 空炸点声学测量系统总体架构
其中,检靶仪的结构组成如图2所示。检靶仪作为声信号采集处理终端,完成声信号的采集、滤波,并通过无线通信将相关数据发送给数传仪,数据经数传仪调制解调传输至上位机(电脑)进行后期处理。上位机根据解调的数据格式,按照程序设定完成声信号的数据处理、时差计算,最终实现单一分站定向,多站实现联合定位。

图2 检靶仪结构组成
1.2 系统处理流程设计
声信号被采集后,经分站转存,通过无线通信发送给中心站进行数据处理、计算。空炸点声学测量系统的整个处理工作流程分为3部分:分站FPGA信号采集流程、分站单片机控制及无线通信流程、中心站数据接收处理流程,分别如图3、图4、图5所示。
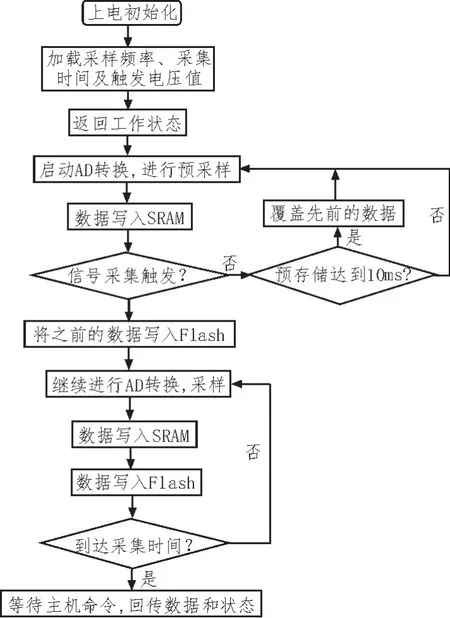
图3 分站FPGA信号采集流程

图4 分站单片机控制及无线通信流程

图5 中心站数据接收处理流程
2 声学传感器性能分析
声学传感器作为声探测系统的“耳朵”,是整个测量系统中最为关键的器件之一,其技术指标和性能优劣直接影响着声信号的采集质量,因此传感器的选取十分重要,既要求其技术指标满足测试需要,又要求一致性要好、可靠性高。同时,考虑靶场所处位置在草原环境中,季节性噪声明显,直接影响传感器误触发率,故结合市面常见的3类传感器进行了噪声特性分析。
传感器的噪声主要有两个来源,即本身的固有噪声和外界引起的噪声。固有噪声主要是由膜片的热扰动或有源电路部分电噪声引起的,其大小用等效噪声级表示[8]。传感器的等效噪声级表示为:

式中,Ln为传感器的A计权等效噪声级,单位为分贝(dBA);Un为A计权网络传感器的固有噪声电压;M为传感器灵敏度;Pr为参考压强,一般取Pr=2×10-5Pa。
参照3种传感器的技术指标,见表1。本底噪声值最大的为CHZ-213自由场型传感器,其本底噪声Ln为16 dBA,传感器灵敏度M为50 mV/Pa,计算得到噪底电压为Un=6.309 57×10-6V。
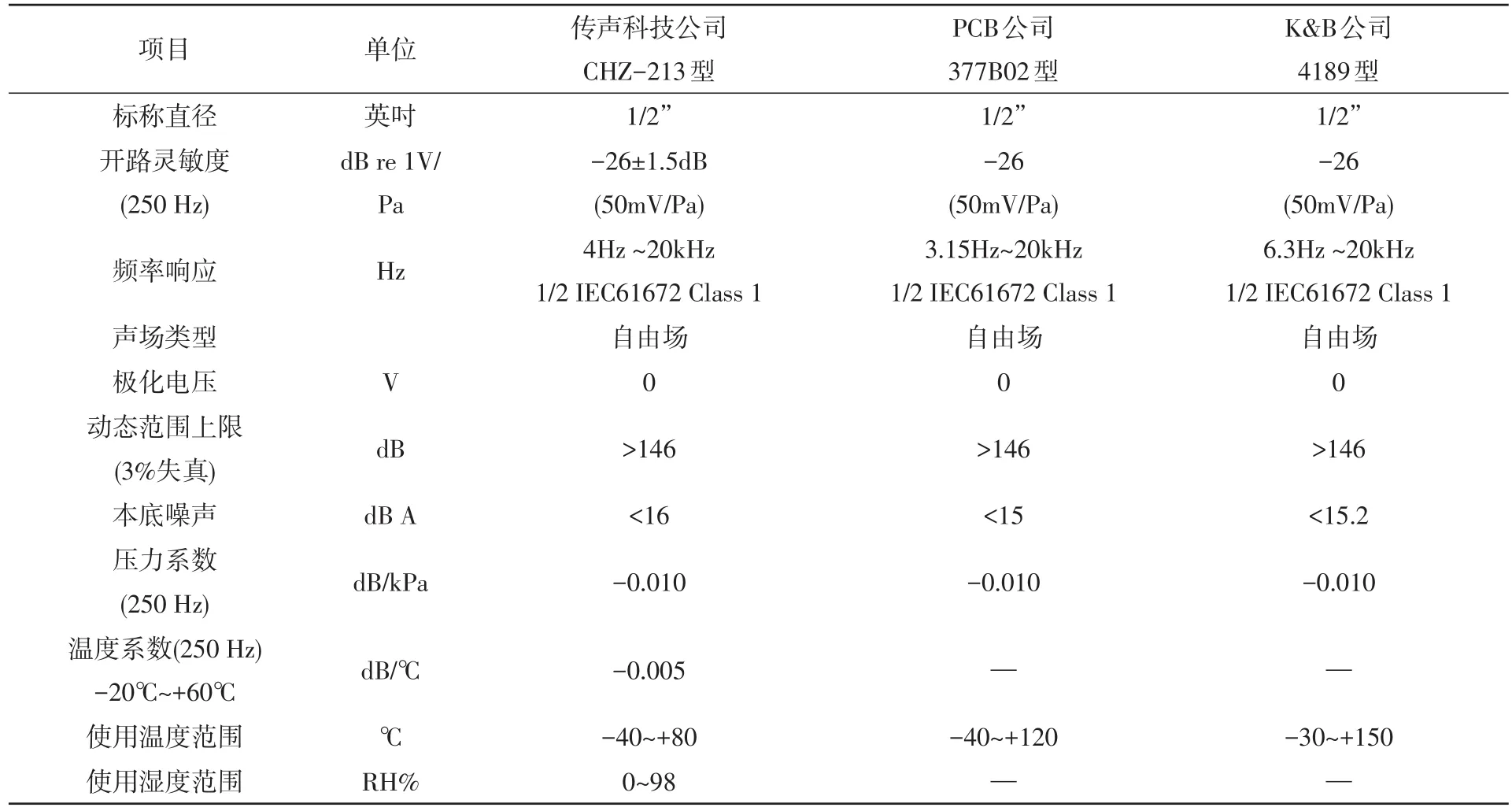
表1 3种传感器技术指标
按照声压级计算公式,见式(2),可计算得到当外部声压达到50 dB时,CHZ-213自由场型传感器测得的理论声压为p=1.58×10-3Pa,其中参考声压p0=20 μ Pa。

此时,传感器的输出电压为:U=M×p=0.05×1.58×10-3=7.9×10-5V,已超过其固有噪底电压Un,可正常触发传感器。通常情况下,草原背景环境噪声在30~40 dB,受季节因素(如季风、虫鸣)影响显现规律性。
现有某型子母弹战斗部开舱时爆炸能量相当于1.5 kgTNT当量,将爆炸过程分冲击波和声波两阶段累加计算,近似得到声波传播10 km后,到达传感器的声压Lp约为115 dB,远高于草原背景噪声;且声波频率特性位于人耳识别区间,声信号可被检测采集,故上述3种传感器均满足指标要求,可综合考虑器件成本、采购周期、后期维护、一致性筛选等因素合理优选。
3 系统关键技术
理论上,利用上述声学传感器通过一定的阵列设计,构成特定数学求解模型,将采集的声信号经过信号处理后,根据提取的时差带入求解模型解算,就可实现单站定向,三站联合定位。虽然被动声定位技术在原理上看似简单,但在工程实际应用中受到诸多因素的影响和制约。
在声学测量系统中,如何提高测量精度是研究的重点和难点,而影响测量精度的主要因素包括传感器阵型、信号处理方法、时延估计算法等。
3.1 传感器阵型优化
传感器阵型主要分为两大类,一是以单基阵为研究对象,研究如何改变一定数量传感器间的几何排布来提高定向性能;另一类是以复合阵为研究对象,每个复合阵由若干单基阵构成,通过研究复合阵的不同阵型排列,提高整体的定位精度。
典型几种单基阵阵型包括[9-11]:直线阵、圆阵、四方阵、平面五元十字阵等,如图6所示。

图6 几种典型单基阵阵型
通过阵型特性分析,直线阵无法完成空中目标的三维定位,至多只能确定其中的二维参量。圆阵具有良好的测距性能,但其测距、侧向的方差仅与时延估计、声速以及基阵的阵径有关,而与目标方位无关,抑制了时延估计方差对测距和侧向精度的影响。四方阵由于阵型限制,不能进行远距离定位,阵列冗余度较小。平面五元十字阵是五元阵的经典阵型,在方位角估计方面,克服了四方阵测向时受目标方位角影响的缺点,但俯仰角估计存在误差较大的问题。
为了提高俯仰角测量精度,本文在保留平面五元十字阵测量方位角优势的基础上,增加了Z轴方向的测试分量,有效提升了对空中目标的定向能力。立体五元十字阵阵型如图7所示。
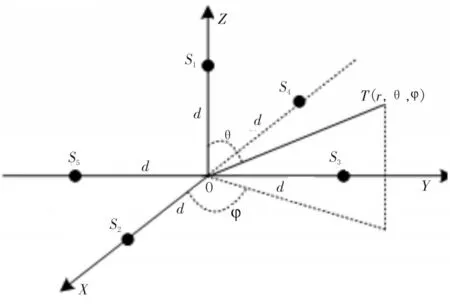
图7 立体五元十字阵阵型
立体五元十字阵可满足对空中目标方位和俯仰的有效测量,构建此单基阵的基础上,可借鉴光学空间几何交汇方法[12]实现三基阵的联合定位,文中不再赘述。
3.2 信号处理方法
鉴于靶场试验环境复杂,传感器采集的信号中可能掺杂多种非目标信号,例如:风声、虫鸣声、油机的轰鸣声等,这些噪声在一定程度上直接影响目标声源的定位精度。保证定位精度就需要剔除这些与爆炸波不一致的内嵌噪声,首要完成的就是数据的预处理。
通常数据预处理是一种为优化系统性能而采取的措施,本系统采用了一种新颖的数据预处理方法—全相位数据预处理方法[13]。该方法将输入数据长度为(2N-1)的数据向量x=[x(n+N-1),…,x(n),…,x(n-N+1)]T转化为长度为N的数据向量x1=[x1(0),x1(1),…,x1(N-1)]T。其中,向量x1可以看成用卷积窗对向量x进行数据加权后,将左边各数据向右平移N个延时单元,再与位置重叠的另一个数据相加而得到。
与传统数据预处理方法相比,采用全相位数据预处理摒除了以某些特定任务或目标为需求的情景设定,数据经过全相位预处理后,保留了丰富的相位信息,使得此后再进行传统频谱分析、滤波等操作就变成了全相位频谱分析、全相位滤波,系统性能得到进一步优化。
数据经过预处理后,若想取得良好的滤波效果,还需明确干扰源的特性,包括频率、幅值等信息,这里需要考虑两种情况。第一种情况:若干扰源的频段与目标信号的频率互不叠加且相差较大,可设计一个带阻数字滤波器,截止干扰源频段的两个边界点。第二种情况:若干扰源频段与目标信号的频率有叠加,这样利用频域差异不能将目标声信号提取出来,只能从幅值及动态特性入手。
经实测分析,弹丸爆炸所产生的声信号是突发的、短暂的;而通常干扰源产生的信号在一定时间内是呈现周期性的,频率和幅值变化不大。因此,可以设计一个递推平均滤波器进行处理。需要注意的是,滤波处理必然对系统时间戳产生一定位移,可以利用补偿方法使时间与波形相对应,以抵消由此带来的系统误差。
3.3 时延估计算法
时差定位法是目前在对声源定位中应用最为广泛的一种方法。在利用时差定位法进行定位时,首先需要确定同一目标声源到达不同传感器之间的时间差。然后,结合传感器阵列模型通过一定的几何算法,利用已测得的时间差实现定位。因此,能否获得精确的时间差将直接影响定位的准确性。
互相关函数法既适合连续信号的时延估计,也适用于突发性信号的时延估计[14],有着广泛的应用;其原理是先对两个独立传感器接收到的两个离散信号进行滤波,然后求得两者的互相关函数,相关函数的峰值所对应的时间即为时延估计值。目前,许多学者在原有广义相关法的基础上进行了改进,提出了广义相位时延估计、基于小波变换的广义相关时延估计算法和LMS时延估计算法等[15]。
考虑到计算任意两个传感器接收信号的互相关函数时,需用到权函数,此类方法往往要知道信号和噪声的先验知识,这在工程应用中较难获得;同时,此种算法假设条件中信号是平稳的,限制了其应用范围。于是,有人提出用自适应滤波器来代替广义相关法的预想滤波器,设计了自适应时延估计算法,此方法对于噪声类型为高斯噪声具有一定借鉴意义;但是在非高斯噪声环境下,适应性较差。
因此,文中借鉴了文献[16]的思想,引入了“相关熵”的概念,其作为随机变量间局部相似性的度量,是一种能够反映其分散系数信息的统计量,被证明可作为自适应时延估计算法的代价函数来进行时延估计。应用广义相关熵函数法可通过构造基本的相关熵函数,利用搜索相关熵函数的极大值来估计时延值。此算法在非高斯噪声环境下不仅估计精度和抗造性能优异,并且算法执行难易程度与经典互相关算法相同[16],有较强的适应性。
4 结束语
本文以被动声定位技术应用于常规武器弹药试验空炸点或开舱点测试问题为切入点,设计了一种空炸点声学测量系统,在弹道偏差大、目标特性弱、落弹区地形复杂等特殊条件下,提供了一套声学解决方案。在对系统总体方案设计的基础上,明确了系统总体架构和结构组成,细化了分站和中心站关键处理流程。通过性能分析和实例计算,验证了声学传感器完成爆炸信号检测采集的可行性;并重点分析了影响空炸点测量精度的3项关键技术,为最终实现系统功能、保证测量精度提供了理论基础和技术支撑。
参考文献:
[1]李翰山,雷志勇.多幕光学法测量弹丸炸点坐标及误差分析[J].光学学报,2012,32(2):129-135.
[2]董涛,倪晋平.能识别弹丸飞行方向的弹丸空间炸点三维坐标测试方法[J].光学技术,2011,37(4):406-411.
[3]冯杰,杨博,李兆利.空气声探测在军事中的应用[J].电声技术,2012,36(6):32-36.
[4]许志勇,赵兆,沈曙明.单兵反狙击声频探测与定位技术概述[J].电声技术,2015,39(2):38-40.
[5]陆伟.法国陆军接收车载狙击手定位系统[J].国外坦克,2012(2):4-4.
[6]张小华.狙击手声学定位系统试验样机研制[D].哈尔滨:哈尔滨工程大学,2014.
[7]杨俊梅,方厚林,成龙,等.反狙击系统传感器阵列的设计[J].声学技术,2014,33(4):381-384.
[8]蒋东东,狄长安.八点线式声学立靶弹着点检测系统研究[J].电子测量技术,2010,33(4):19-21.
[9]周成胜,王新喆,孙胜红,等.传声器直线阵列在声源定位问题中的误差分析[J].电声技术,2016,40(4):26-28.
[10]陆丽.基于声传感器阵列的目标方位估计方法[D].镇江:江苏科技大学,2016.
[11]马少春,刘庆华,黄灵鹭.基于相关峰插值的五元十字阵被动声定位算法[J].探测与控制学报,2014,36(5):94-98.
[12]李翰山,雷志勇.基于摄像法测量弹丸的空间炸点位置[J].光学精密工程,2012,20(2):329-336.
[13]黄翔东,王兆华.全相位数字谱分析方法[M].北京:科学出版社,2017.
[14]金中薇,姜明顺,隋青美,等.基于广义互相关时延估计算法的声发射定位技术[J].传感技术学报,2013,26(11):1513-1518.
[15]孙洋,徐慨,杨海亮.基于广义互相关时延估计算法的性能分析[J].计算机与数字工程,2013,41(1):33-34.
[16]佟祉谏.Alpha稳定分布噪声环境下基于相关熵的时延估计算法研究[D].大连:大连理工大学,2010.

