中深孔崩矿阶段嗣后充填法采场结构参数优化

兰明，刘志祥，李夕兵，刘强

中深孔崩矿阶段嗣后充填法采场结构参数优化

兰明，刘志祥，李夕兵，刘强

(中南大学 资源与安全工程学院，湖南 长沙，410083)

为获得合理采场结构参数，实现山东莱州望儿山金矿中深孔阶段崩矿嗣后充填法的安全高效开采，采用弹性薄板理论，分析不同跨度下顶板应力与厚度的关系，确定合理的开采参数范围；结合矿山实际开采条件，通过中心复合试验设计，采用数值模拟计算得到不同结构参数下的力学响应；基于二阶响应面法建立最大拉应力、最大压应力和竖向最大位移的回归模型；将回归模型作为目标函数，采用遗传算法进行多目标优化，获得Pareto最优解集。研究结果表明：根据工程实际需要，矿房跨度为26.0 m、矿柱跨度为28.0 m及顶板厚度为6.7 m为开采最佳结构参数。

采场结构参数；数值分析；响应面法；遗传算法；多目标优化

望儿山矿区位于山东省莱州市东部金城镇境内，作为焦家金矿三大矿区之一，随着开采深度不断增加，其开采技术条件越来越差，矿区浅部所采用的上向进路充填采矿法逐渐难以维持现有生产能力。为解决生产效率低、开采成本高等问题，矿区提出采用中深孔崩矿阶段嗣后充填采矿法，而确定合理的采场结构参数是实现矿山深部安全高效开采首先需要解决的技术难题[1]。在采场结构参数的研究上，国内外研究者进行了大量研究。刘钦等[2]运用数值模拟结合神经网络及混沌优化等手段，获得了三山岛金矿合理的采场结构参数；李洁慧等[3]采用层次分析结合模糊数学的评价方法，对采场结构参数进行了优选；陶干强等[4]通过有限元软件分析了不同结构参数下的力学响应；BAI等[5]提出了分段回采法采场设计的网络流算法，验证了其合理性并成功应用于工程实际；罗周全等[6]基于弹性理论、数值分析及多目标决策方法对采场参数进行了综合优化；周科平等[7]建立了不同采场参数与安全系数之间的神经网络模型，借助遗传算法对采场结构进行了优化。由此可见，数值模拟手段、非线性优化及多目标决策是研究采场结构参数的几种主要手段。然而，当前方法仍然存在着一些不足之处，如：李洁慧等[3]仅对数值模拟结果进行简单分析，只靠力学响应结果进行优化，BAI等[5]通过神经网络虽然建立了不同结构参数与安全系数之间的映射关系，但仅以安全系数作为目标函数进行单目标优化等。响应面回归模型在结构可靠度分析[8]中运用广泛，在矿业[9]、冶金[10]、食品[11]及生物[12]等工艺参数优化设计中也取得了显著效果，是实现多因素多水平、多目标优化分析的一种有效方法；遗传算法在对非线性功能函数参数寻优[13−15]方面具有强大的优势。为此，本文作者根据望儿山矿区开采实际，通过中心复合试验设计手段，采用数值模拟分析不同结构参数下采场的力学响应，建立不同结构参数与力学响应之间的响应面模型；结合遗传算法进行响应面功能函数的多目标参数优化，综合确定采场结构参数，以便为矿山安全高效开采提供指导。

1 工程概况

望儿山矿区V号矿体赋存于+85.0~−650.0 m范围内，大体走向为5°~15°，自北向西倾斜；−470.0 m中段以上矿体平均厚度为6.7 m，矿体倾角为45°左右，处于开采完毕及残采阶段；−510.0 m中段将成为开采主要地段，其矿体规整，矿体平均厚度为12.5 m，倾角达55°。根据矿山的开采技术条件及现状，−510.0 m中段及其以下矿体变厚，为大规模开采创造了条件。借鉴中厚矿体中深孔爆破开采相关经验，望儿山矿区设计将分段凿岩阶段嗣后充填法作为试验采场的采矿方法，试验采场布置见图1。

从图1可知：采场沿矿体走向布置，分矿房及间柱。矿房采用分段凿岩阶段嗣后充填法回采，采场高度为中段高度(40.0 m)，宽度为矿体厚度(12.5 m)，两侧矿房分3个分段进行中深孔爆破回采。由于该矿−470.0 m中段未铺设人工假底，上部为120.0 m高充填体，采场需留设一定厚度的顶柱，脉内靠近下盘布置中深孔爆破凿岩巷道，以切割天井作为首次爆破自由面及补偿空间，由上自下分层进行中深孔爆破，底部布置无底柱堑沟出矿结构，采用铲运机出矿。待两侧矿房回采完毕，对空区进行嗣后全尾砂胶结充填，然后回采矿柱采场。

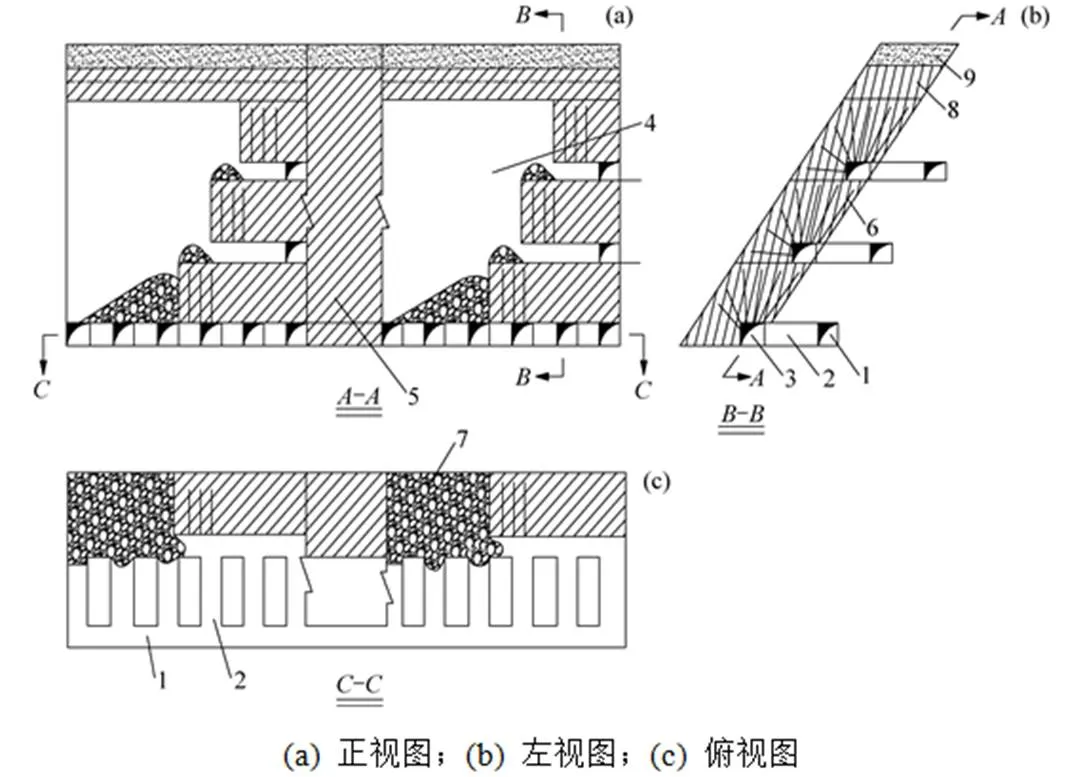
1—脉外运输巷道；2—出矿巷道；3—分段凿岩巷道；4—矿房；5—矿柱；6—中深孔；7—矿石堆；8—顶板；9—上覆充填体。

2 顶板弹性力学分析

针对试验采场的实际布置情况，采场宽度为矿体厚度，采场结构优化问题归结为对顶板留设厚度及采场跨度进行合理取值。研究表明，顶板是影响阶段空场嗣后充填采场的稳定性的1个重要因素，因此，可以通过顶板的受力状态，从理论上获得顶板厚度及跨度的合理取值。

根据弹性小薄板理论，当垂直于板中面的直线在板变形后仍垂直于中面、垂直于中面上的正应力远小于其他应力分量、板中面不受垂直载荷作用发生拉伸变形时，可将空区顶板视为四边固支的弹性板模型。基于上述假设，顶板受到上覆矿岩及充填体的均布载荷的作用，顶板厚度为，跨度为，宽度为，弹性模量为，泊松比为。通过Rayleigh-Ritz法可获得顶板的挠曲函数为

式中：==1，3，5，…。进一步推导可得

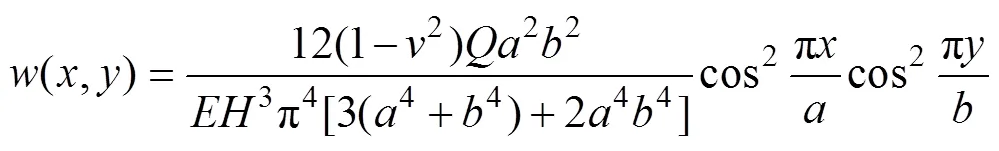
根据弹性力学理论及式(2)，可获得顶板内部应力状态为

式中：1为任意常数，和分别为和方向上的正应力；为剪应力。由(3)式得3个最大应力1，2和3为

据TRESCA屈服准则，顶板内产生剪切屈服的条件为

将式(4)代入式(5)得最大剪应力max为

顶板稳定状态的判断依据为：

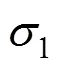
跨度/m：1—35.0；2—30.0；3—25.0。

跨度/m：1—35.0；2—30.0；3—25.0。

3 数值模拟试验

3.1 岩体力学参数及初始地应力场

通过对望儿山矿区−470.0~−510.0 m中段岩体工程地质调查、上下盘围岩取样测试及充填体强度试验，经工程强度折减后获得数值模拟所需的岩体力学参数，见表1。

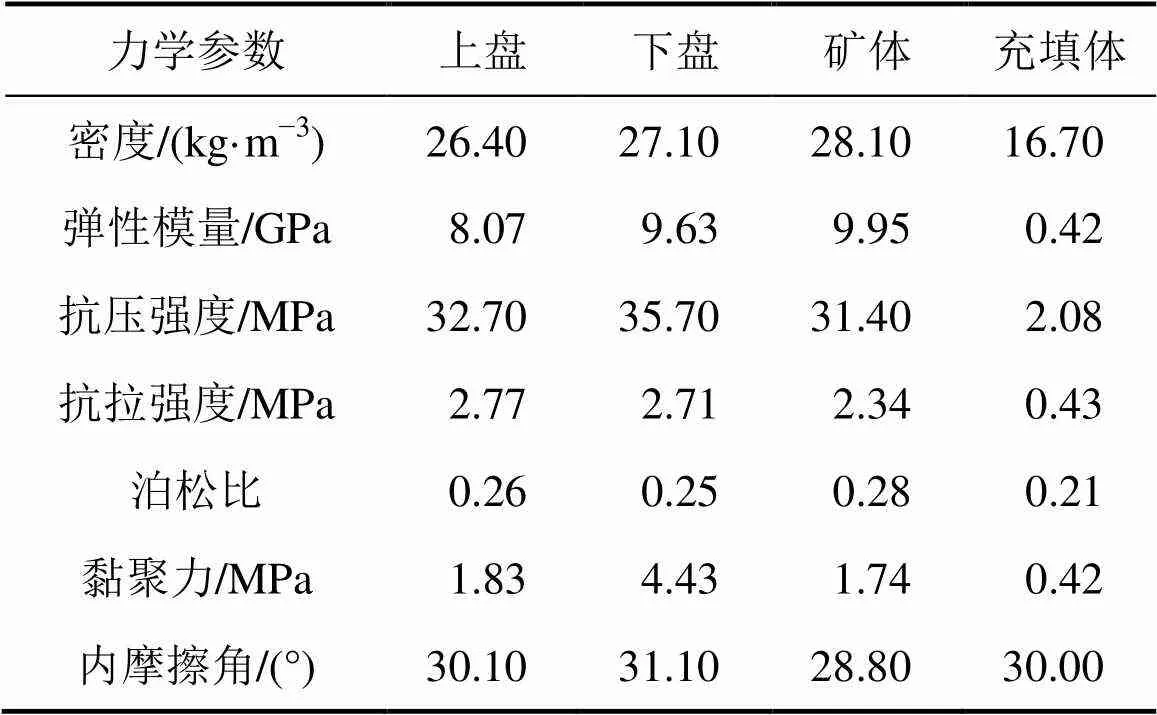
表1 岩体力学参数

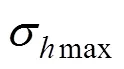
式中：为竖直方向的深度。

3.2 模型构建及计算结果

为研究不同参数对采场稳定性影响，对模型进行适当简化。假设矿体平均厚度为12.5 m，矿体倾角为55°，上覆充填体高度为120.0 m，根据圣维南原理，将开挖范围3~5倍作为模型边界，模型长×宽×高为 200.0 m×160.0 m×200.0 m，见图4。取矿房及矿柱跨度分别为25.0，30.0和35.0 m，控顶厚度分别为5.0，7.0和9.0 m，根据中心复合试验设计原理，共设计15个试验点进行数值模拟分析，各采场参数、水平及数值计算结果见表2。

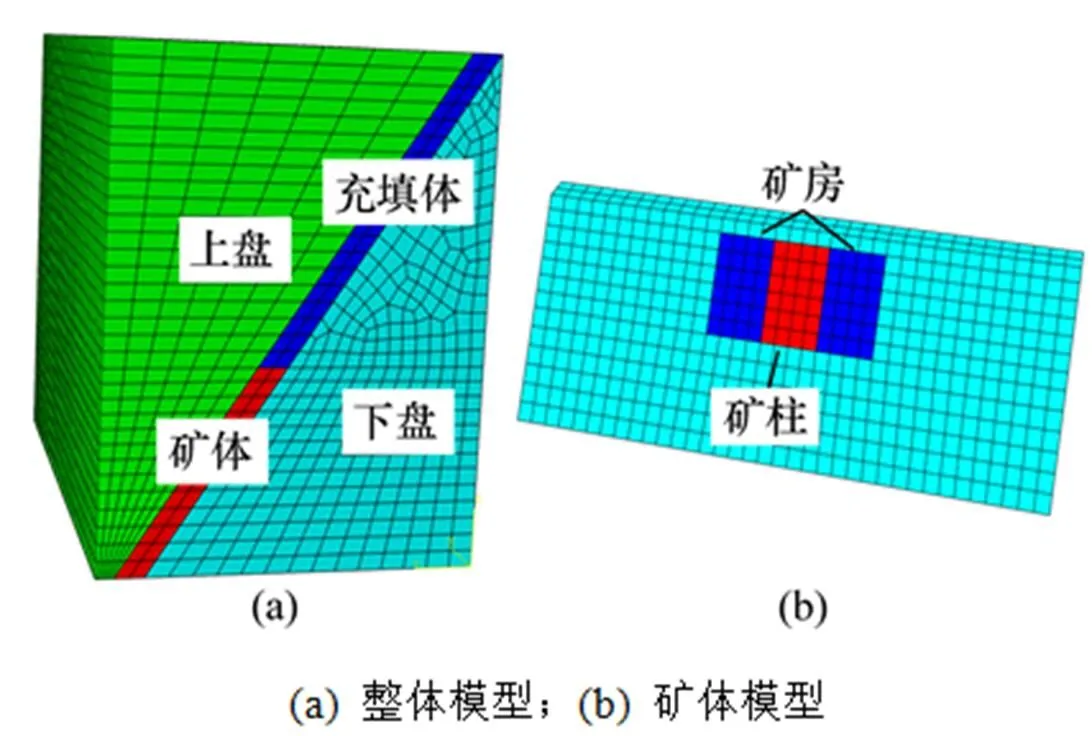
图4 有限元分析模型图

表2 各方案力学响应指标比较结果

结果表明：采场开挖后均出现拉应力，主要集中于顶板靠近上盘附近；所有方案中，最大拉应力为2.184 MPa，未超过矿体的抗拉强度2.34 MPa；采场最大主应力为15.03~16.40 MPa，表现为压应力；最大竖向位移范围为1.861~3.628 cm。由此可见：上述方案采场应力及位移均在合理范围内，采场未发生破坏。

4 采场结构参数多目标优化

4.1 响应面模型建立

根据表2中各方案采场参数值及力学响应结果，建立矿房跨度1、矿柱跨度2及顶板厚度3与采场最大拉应力1、最大压应力2及最大竖向位移3之间的响应面模型。考虑到一阶线性响应面模型拟合精度通常较低，结合采用二阶非线性响应面模型建立采场参数与各力学响应之间的映射关系，模型的基本表达式为

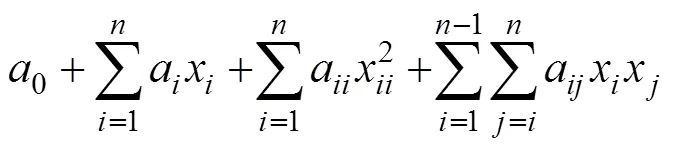
对3个响应面模型进行拟合，剔除不显著影响项，得到响应面模型如下：

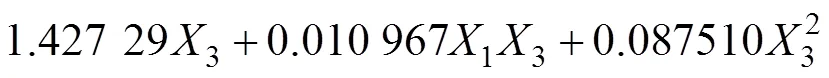
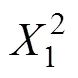
回归模型1中，不含有参数1(矿房跨度)的影响项，说明矿房跨度对最大拉应力的影响不显著，而矿柱跨度及顶板厚度及两者之间的交互作用对最大拉应力有显著影响。图5所示为矿柱跨度与顶板厚度交互作用对最大拉应力影响的响应曲面。

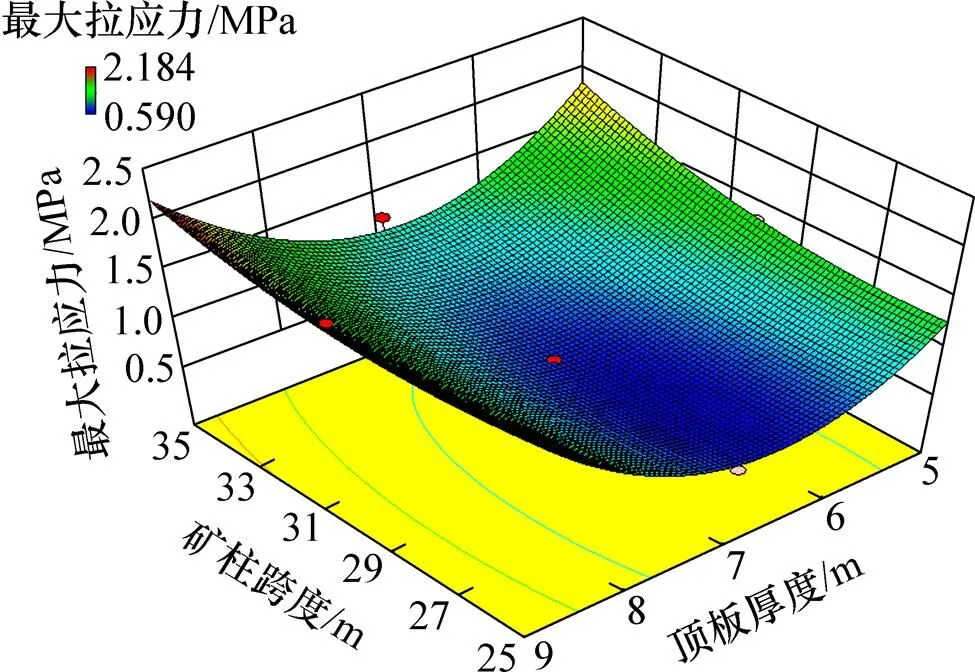
图5 矿柱跨度与顶板厚度对最大拉应力响应曲面

从上述回归模型可知：采场应力、竖向位移受到不同参数及其交互作用的影响，对单一模型进行优化意义不大。因此，必须综合考虑各结构参数与不同响应之间的关系进行多目标综合优化。

4.2 Pareto遗传算法多目标参数优化

研究认为[17−18]，在工程实际多目标优化问题中，几乎不存在1个使所有目标达到最优的最优解。传统的一些多目标优化方法如加权组合法、目标规划法等都需进行求导处理，且易陷入局部最优。遗传算法的随机性及隐含并行性使其具有强大的全局搜索能力，结合Pareto最优的遗传算法能够得到Pareto最优解集，可选出满足设计需要的解。

求解Pareto最优解集的核心思想，是对于以下多目标优化问题：

有变量1∈，2∈(为变量约束集)，对所有目标函数均有f(1)≤f(2)(=1，2，…，)，并至少存在1个目标函数使得f(1)＜f(2)，则变量1支配2，记为1＞2。中不存在变量和使得＞，那么，为中的非支配变量，这样的变量就是多目标优化问题中的Pareto最优解。Pareto最优解往往不只1个最优解，而是以集合的形式出现，因此，多目标优化的关键在于找出尽可能多的最优解。

基于以上原则，运用Matlab软件，采用遗传算法对式(10)~(12)进行Pareto解的寻优，经过138次迭代，获得采场参数多目标优化问题的Pareto最优解集。图6所示为目标优化问题的Pareto前沿，其Pareto解值及所对应的参数见表3。

按照工程实际需要，顶板留设厚度适当减小，可以减少矿石损失，而中深孔阶段嗣后充填采场跨度适当增加，有利于提高生产效率。因此，将表3中最优解1(即矿房采场跨度为26.0 m，矿柱采场跨度为 28.0 m，顶板留设厚度为6.7 m)作为结构参数的优化结果，其采场应力及位移均在极限开采尺寸的可控范围内，可以满足工程设计需要。

图6 目标优化问题的Pareto前沿点

表3 遗传算法多目标寻优结果

5 结论

1) 由弹性小薄板理论分析了采场顶板受力状态与矿房、矿柱跨度及顶板厚度之间的关系，确定了采场安全开采的合理参数范围，即顶板留设厚度不小于5.0 m，采场跨度不超过35.0 m。

2) 通过中心复合试验手段，采用数值模拟获得不同采场参数下最大拉应力、最大压应力及最大竖向位移。建立了不同参数与各力学响应之间的二阶响应面模型，剔除了非显著性交叉项的影响，得到各模型拟合系数2分别为0.992 3，0.976 9和0.893 9，表明模型拟合度较高，可用于参数寻优。

3) 将基于Pareto最优解集的遗传算法应用于响应面模型的多目标优化问题中，获得采场结构参数的17个非劣解。根据工程实际需要及相关原则，将矿房采场跨度26.0 m、矿柱采场跨度28.0 m及顶板留设厚度6.7 m作为开采的最优结构参数。

[1] 汪伟, 罗周全, 秦亚光, 等. 无底柱深孔后退式崩矿法采场结构参数优化[J]. 东北大学学报(自然科学版), 2016, 37(4): 578−582. WANG Wei, LUO Zhouquan, QIN Yaguang, et al. Stope parameters optimization of non-pillar longhole retreat caving[J]. Journal of Northeastern University(Natural Science), 2016, 37(4): 578−582.

[2] 刘钦, 刘志祥, 刘爱华, 等. 金矿采场结构参数混沌优化[J]. 采矿与安全工程学报, 2010, 27(4): 548−552.LIU Qin, LIU Zhixiang, LIU Aihua, et al. Chaotic optimization of structural parameters in gold mining field[J]. Journal of Mining & Safety Engineering, 2010, 27(4): 548−552.

[3] 李洁慧, 王新民, 张钦礼, 等. 采场结构参数的层次分析和模糊数学综合评价[J]. 化工矿物与加工, 2009, 38(9): 23−27. LI Jiehui, WANG Xinmin, ZHANG Qinli, et al. Stope structural parameters optimization based on AHP and fuzzy mathematics[J]. Industrial Minerals and Processing, 2009, 38(9): 23−27.

[4] 陶干强, 孙冰, 宋丽霞, 等. 充填法采场结构参数优化设计[J]. 采矿与安全工程学报, 2009, 26(4): 460−464.TAO Ganqiang, SUN Bing, SONG Lixia, et al. Optimal design of stope structural parameters using back-filling method[J]. Journal of Mining & Safety Engineering, 2009, 26(4): 460−464.

[5] BAI X, MARCOTTE D, SIMON R. Underground stope optimization with network flow method[J]. Computers & Geosciencs, 2013, 52(1): 361−371.

[6] 罗周全, 汪伟, 谢承煜, 等. 倾斜中厚矿体采场宽度优化[J]. 中南大学学报(自然科学版), 2015, 46(10): 3865−3871. LUO Zhouquan, WANG Wei, XIE Chengyu, et al. Optimization of stope width of inclined medium thick ore body[J]. Journal of Central South University (Science and Technology), 2015, 46(10): 3865−3871.

[7] 周科平, 王星星, 高峰. 基于强度折减与ANN-GA模型的采场结构参数优化[J]. 中南大学学报(自然科学版), 2013, 44(7): 2848−2854. ZHOU Keping, WANG Xingxing, GAO Feng. Stope structural parameters optimization based on strength reduction and ANN-GA model[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2848−2854.

[8] 李静萍, 程勇刚, 李典庆, 等. 基于多重响应面法的空间变异土坡系统可靠度分析[J]. 岩土力学, 2016, 37(1): 147−155.LI Jingping, CHENG Yonggang, LI Dianqing, et al. System reliability analysis of spatially variable soil slope using the multiple response surfaces method[J]. Rock and Soil Mechanics, 2016, 37(1): 147−155.

[9] 赵国彦, 马举, 彭康, 等. 基于响应面法的高寒矿山充填配比优化[J]. 北京科技大学学报, 2013, 35(5): 559−565.ZHAO Guoyan, MA Ju, PENG Kang, et al. Mix ratio optimization of alpine mine backfill based on the response surface method[J]. Journal of University of Science and Technology Beijing, 2013, 35(5): 559−565.

[10] LI Zhiqqiang, LI Jing, ZHANG Libo, et al. Response surface optimization of process parameters for removal of F and Cl from zinc oxide fume by microwave roasting[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(3): 973−980.

[11] LAZO-VÉLEZ M A, AVILÉS-GONZÁLEZ J M, SERNA-SALDIVAR S O, et al. Optimization of wheat sprouting for production of selenium enriched kernels using response surface methodology and desirability function[J]. LWT-Food Science and Technology, 2016, 65(1): 1080−1086.

[12] BUKZEM A L, SIGNINI R, SANTOS D M, et al. Optimization of carboxymethyl chitosan synthesis using response surface methodology and desirability function[J]. International Journal of Biological Macromolecules, 2016, 85: 615−624.

[13] RUISECO J R, WILLIAMS J, KUMRAL M. Optimizing ore–waste dig-limits as part of operational mine planning through genetic algorithms[J]. Natural Resources Research, 2016, 25(4): 1−13.

[14] FUZEAU J, VASUDEVAN M, MADURAIMUTHU V. Optimization of welding process parameters for reduced activation ferritic-martensitic (RAFM) steel[J]. Transactions of the Indian Institute of Metals, 2016, 69(8): 1−7.

[15] LIN H Y, LIN C J, HUANG M L. Optimization of printed circuit board component placement using an efficient hybrid genetic algorithm[J]. Applied Intelligence, 2016, 45(3): 1−16.

[16] THIRUGNANASAMBANDHAM K, SIVAKUMAR V, PRAKASH M J. Optimization of electrocoagulation process to treat biologically pretreated bagasse effluent[J]. Journal of the Serbian Chemical Society, 2014, 79(5): 613−626.

[17] 程文渊, 崔德刚. 基于Pareto遗传算法的复合材料机翼优化设计[J]. 北京航空航天大学学报, 2007, 33(2): 145−148. CHENG Wenyuan, CUI Degang. Optimization for composite wing based on Pareto genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(2): 145−148.

[18] 张永, 吴晓蓓, 徐志良, 等. 基于Pareto多目标遗传算法的模糊系统设计[J]. 南京理工大学学报, 2007, 31(4): 430−434. ZHANG Yong, WU Xiaobei, XU Zhiliang, et al. Design of fuzzy systems based on pareto multi-objective genetic algorithm[J]. Journal of Nanjing University of Science and Technology, 2007, 31(4): 430−434.

(编辑 陈灿华)

Stope parameters optimization of level afterwards back-filling approach with medium-deep hole caving

LAN Ming, LIU Zhixiang, LI Xibing, LIU Qiang

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

In order to obtain the rational stope structure parameters and realize safe and efficient mining of level afterwards back-filling approach with medium-deep hole caving in Wangershan Gold mine. The changing relationship between stress and thickness of roof under different spans was analyzed by using the thin elastic theory, the rational range of excavating was determined. Combined with the actual mining condition, through the central composite test design, mechanical responses under different structural parameters were obtained by numerical simulation. Based on the second order response surface method, the regression models of the maximum tensile stress, the maximum compressive stress and the maximum vertical displacement were established and regarded as objective functions, the Pareto optimal solution set was obtained by genetic algorithm multi-objective optimization. The results show that according to engineering needs, the optimal parameters are as follows: the chamber span is 26.0 m, the pillar span is 28.0 m, and the roof thickness is 6.7 m.

stope structure parameters; numerical analysis; response surface method; genetic algorithm; multi-objective optimization

TD853

A

1672−7207(2018)04−0933−07

10.11817/j.issn.1672−7207.2018.04.022

2017−07−08；

2017−09−22

国家自然科学基金重点资助项目(41630642)；国家自然科学基金资助项目(51674288)；湖南省研究生科研创新项目(CX2016B052)(Project(41630642) supported by the Key Program of the National Natural Science Foundation of China; Project(51674288) supported by the National Natural Science Foundation of China; Project(CX2016B052) supported by the Graduated Student Research Innovation Fund of Hunan Province)

刘志祥，教授，博士生导师，从事金属矿山开采及灾害防控技术研究；E-mail：CSU_LM@163.com