考虑市场力风险约束的最优AGC控制模型
赵万宗,韦 化,韦昌福,鲍海波
(1. 广西大学 广西电力系统最优化与节能技术重点实验室,广西 南宁 530004;2. 广西电网电力调度控制中心,广西 南宁 530023)
0 引言
自动发电控制AGC(Automatic Generation Control)是实现电力系统供需平衡的重要技术手段。随着新一轮电力市场改革的重启[1],将竞争机制引入AGC辅助服务成为发展趋势,由此带来的市场力风险[2]必将影响AGC辅助服务市场正常运行。
现有满足控制性能标准(CPS)[3]的AGC控制策略中,通常关注机组的安全约束,未涉及市场力风险的问题。文献[4-12]研究了CPS下的AGC控制问题,构建满足CPS的AGC控制模型,但未考虑市场力的影响。为了维护市场秩序,降低电网企业购买AGC辅助服务的价格风险,保障用电的可靠性和经济性,文献[13-14]研究了降低市场力的策略及其抑制措施,提出了如引入电力需求弹性、采取长期合约方式、设置价格上限等技术手段,可在一定程度上降低市场力的影响。现有AGC优化控制研究成果难以同时兼顾市场力风险、安全约束和CPS考核指标三者,使得发电商容易滞留容量,抬高AGC调节成本,降低系统运行经济性,存在安全隐患。
因此,本文引入了金融领域广泛采用的风险价值(VaR)方法[15],构建了满足CPS下计及市场力风险的最优AGC控制的混合整数非线性规划MINLP(Mixed Integer NonLinear Programming)模型。模型中综合考虑了CPS考核指标、市场力风险、电力系统安全性与经济性等方面的安全约束条件,并以广西电网运行数据作为测试算例,验证了所提模型的有效性。
1 AGC辅助服务的市场力风险分析
1.1 AGC辅助服务市场框架
AGC辅助服务是电力市场正常运营的一项重要保障,具有公共服务性质,目前国内外主要有库联营(集中竞价)、双边交易型和混合模式等交易模式。迄今为止,AGC辅助服务尚未形成一个统一成熟的市场框架,鉴于AGC辅助服务具有强制性的公共服务性质,需要一个核心管制执行机构(如电网调度中心),来保障辅助服务的正常获取和调度,不失一般性,本文选取集中竞价的市场交易框架。
AGC辅助服务市场由物理环境和市场环境两部分组成,如图1所示。AGC辅助服务提供者按照市场规则向交易中心(或调度机构)提交容量报价和电量报价,由交易中心(或调度机构)根据一定的优化策略,确定向谁购买,以及购买的容量价格。市场参与者除了可以调整报价策略外,没有其他自主选择的权力。

图1 AGC辅助服务市场基本结构Fig.1 Basic structure of AGC ancillary service market
由于市场交易中心所确定的AGC机组是未来一段时间内预期投入的机组,其是否会在实时调度中被选择,则由实时调度控制策略来确定,即AGC辅助服务市场由日前市场和实时市场两部分构成,如图2所示。日前市场选中的机组,无论其是否参与实际调节,均可获得相应的容量备用补偿,在本文的优化目标中将此部分忽略。实际参与调节的AGC机组及其调节量的多少,则根据日前市场所选定的机组报价,通过实时控制策略来确定是否下令调节,其结果将影响AGC辅助服务的电量成本。
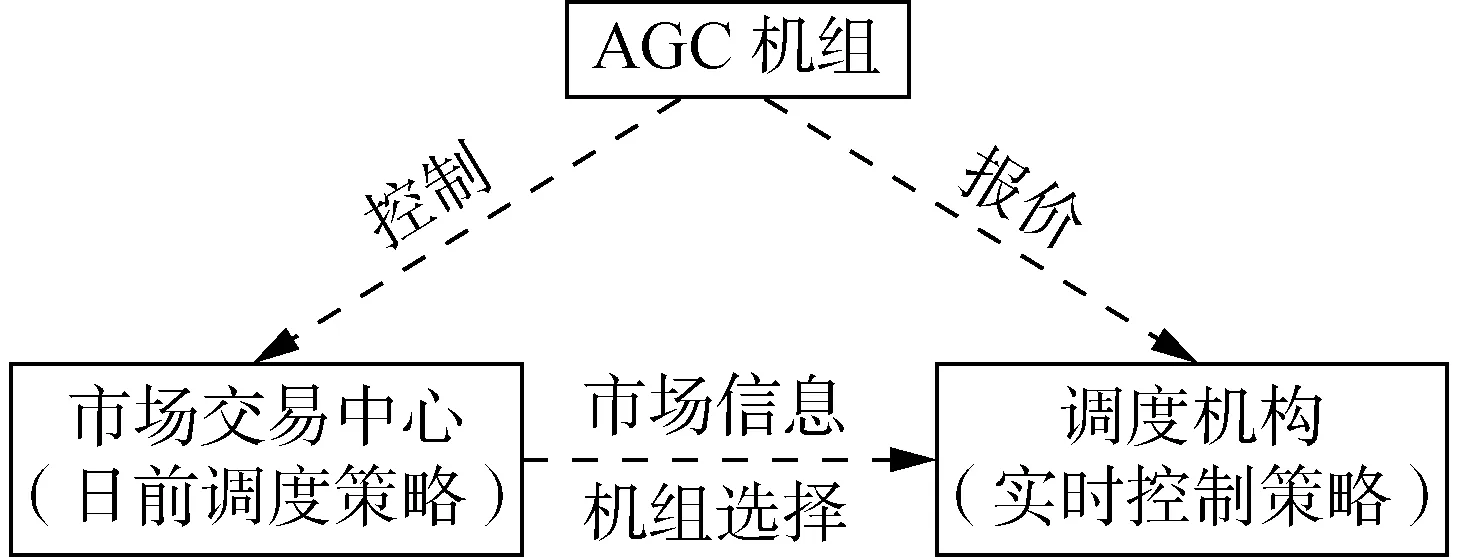
图2 AGC控制基本环节Fig.2 Basic sectors of AGC
1.2 AGC市场力风险建模
传统衡量市场力的指标主要有HHI(Herfindahl-Hirschman Index)、Lerner Index、PCMI(Price Cost Margin Index)等,这些指标一般仅用于事后分析,作为市场力检测的粗略扫描工具[16],难以在实时的优化控制策略中予以考虑。VaR方法对市场风险的表示简洁直观,且适用于事前风险计算,可有效克服传统风险评估事后分析的不足,已成为金融领域风险测量的主流方法。
电网企业愿意承担的市场力风险,可用VaR进行描述,具体表达公式如下:
P(ΔX≤ZVaR)=α
(1)
其中,ΔX为观察期内的损失或风险;ZVaR为给定置信水平α下的最大损失或最大风险上限。
正常负荷波动下,假设辅助服务市场价格服从正态分布,即x~N(μ,σ2),如图3所示,μ为期望成本,σ为标准差,可将其转换为标准正态分布:

(2)
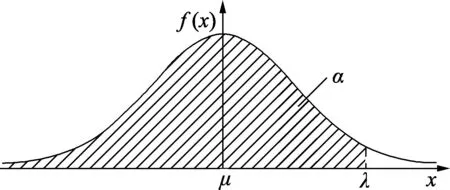
图3 市场价格概率分布示意图Fig.3 Schematic diagram of probability distribution of market prices
采用参数分布法根据历史价格分布,模拟市场交易价格和辅助服务的购买成本,得到电网公司购买成本的分布,进而算出ZVaR值。ZVaR值源于历史价格分布的统计学原理,可实时动态滚动调整,为各方所接受,不具强制性,与政府主导的具有行政强制性的价格上限具有本质差别,且ZVaR值可作为市场参与者进行市场定价或竞价的参考。
在置信水平α下,定义电网公司可接受的风险价格为λ,由式(1)可得:
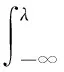
(3)
根据式(3)计算出置信水平α下的风险价格λ,显然,置信水平越高,λ越大,表明对系统价格风险的厌恶程度越低,可承受的价格成本也越大。但在实际应用中,针对采用分布参数方法计算λ值时,可能存在“厚尾”缺陷问题,可通过对比历史风险值,适当调整置信水平,使得风险值趋于合理接受范围。
在AGC考核周期T内,假设备用需求为D,则辅助服务期望成本为μD,置信水平α下的最大风险成本CVaR为:
CVaR=λD
(4)
因此,由负荷波动或新能源随机性波动所导致的辅助服务风险应在可控范围内,则置信水平α下,电网企业愿意承担的经济风险应满足以下约束条件:
(5)

2 考虑市场力风险的AGC优化模型
2.1 满足CPS的AGC优化模型
以省级电网控制区为研究对象,与之相连的外部区域可视为一虚拟控制区,通过虚拟联络线相连。AGC控制策略的输入量主要有系统交易信息(中标AGC机组及其报价、系统出力计划、联络线计划等)、联络线功率偏差Δptie和系统频率偏差Δf、系统负荷预测PL等,如图4所示。由于10min的超短期负荷预测值PL已经相当精确,Δf可根据负荷预测和系统初始出力值按照负荷频率关系进行换算得到。图中,P0为系统预期出力,P为系统实际出力,ΔP为系统预期总调节量。
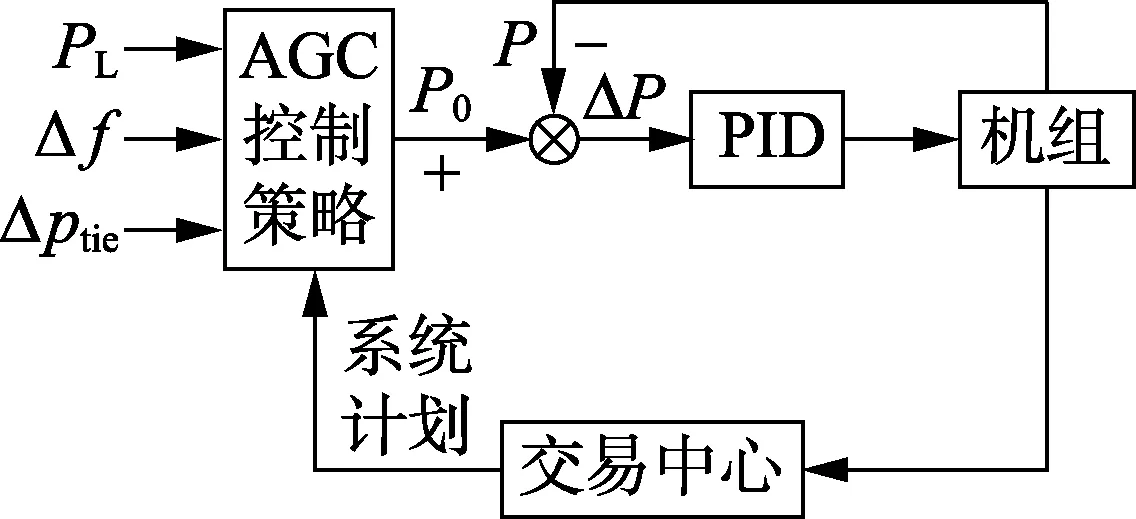
图4 AGC控制过程简图Fig.4 Description of AGC control process
根据AGC控制过程,基于频率与联络线功率偏差控制TBC(Tie-line frequency Bias Control)模式,以电网企业向AGC机组支付的辅助服务费最小为目标,建立模型如下。
(1) 经济性目标函数。
(6)
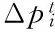
(2) 系统功率平衡约束。
(7)
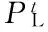
(3) 风险约束。
在考核时段T内,电网企业支付的AGC辅助服务费用应控制在一定的风险水平以下,则:
(8)
其中,CVaR表示一定置信水平α下,电网企业愿意承担的最高风险成本。置信水平越高,表明电网企业对市场风险的厌恶程度越低,控制越稳健,控制成本越高;反之,置信水平越低,愿意承担的价格水平越低,控制成本也越低。
(4) CPS1指标约束。
(9)
(10)

(5) CPS2指标约束。
(11)
其中,L10为规定的ACE控制极限值。
(6) AGC调节容量约束。
(12)
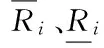
(7) AGC机组有功出力约束。
(13)

(8) 联络线功率约束。
(14)

(9) 最小加减速时间约束。
(15)
(16)

2.2 模型的线性化处理

(1) 机组指令状态变量的等效表达。
(17)

仅通过式(17)只能确保同一台机组在同一时段保持一种可行出力状态,为了避免同一时段既有增出力又有减出力的不合理下令状态,还需要增加如下辅助约束:
(18)
(19)
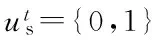
(2) AGC机组调节容量约束。
机组i的新增出力可表示为:
(20)

寓言的标题本来就要求短而精,如果照着原语的标题直接翻译,译语的标题就变得繁琐,不仅违背寓言标题的本身要求还会不符合译语的表达习惯。读过《伊索寓言》英文版,都知道当中的寓言标题大都是简洁的名词或者名词性短语。所以,译者将原语的信息大多删去,只留译代表核心内容和思想的“疑”。
将式(20)代入式(12),可将其转化为:
(21)
(3) 最小加减速时间约束。
非线性约束式(15)可等效为线性约束式(22)—(24):
(22)
t=Gi+1,…,T-UT,i+1
(23)
t=T-UT,i+2,…,T
(24)

同理,非线性约束式(16)可等效为线性约束式(25)—(27):
(25)
t=Li+1,…,T-DT,i+1
(26)
(27)

3 计算结果与讨论
以广西电网某日运行数据作为测试算例,在GAMS平台上调用CPLEX优化工具包进行计算。假设该测试系统投入的AGC机组由日前市场竞价确定,系统中各电厂具体参数如表1所示。CPS指标每10min考核一次,采样间隔为5s,全天144个考核点,L10=120,B=145,联络线功率偏差限值为±100MW, 计算收敛精度为10-6。

表1 AGC电厂参数Table 1 Parameters of AGC plants
为了对比电网企业愿意承担的市场风险对AGC控制的影响,需要选择较高的置信水平[18],这与电力系统要求较高安全运行水平相一致。因此,本文考虑以下2种测试模式。
a. 95%置信水平:市场风险置信水平α为95%情况下,求以AGC机组调节费用最小为目标的最优AGC下令及CPS指标值。
b. 99%置信水平:市场风险置信水平α为99%情况下,求以AGC机组调节费用最小为目标的最优AGC下令及CPS指标值。
表2为2种测试模式下,全天AGC机组下令和CPS1考核情况比较。

表2 全天机组下令及CPS1考核情况比较Table 2 Comparison results for orders and CPS1
图5和图6分别为2种测试模式下全天CPS1和CPS2趋势图。置信水平越高,系统对价格风险的厌恶程度越低,计算结果表明,99%置信水平下的全天AGC机组下令次数比95%置信水平下增加了3.9%,CPS1指标超过200%的考核点增加了37.5%,且无论风险置信水平的高低,均能确保CPS指标合格率100%,满足AGC机组安全约束和电网运行风险水平。置信水平越高,越有利于系统频率的恢复,但付出的调控成本更高。

图5 CPS1趋势图Fig.5 Trends of CPS1

图6 CPS2趋势图Fig.6 Trends of CPS2
以某10min考核时段为例,分析2种测试模式对区域控制偏差ACE、联络线功率等各项参数指标的影响。
(1) ACE。
图7为ACE趋势图;图8为每分钟ACE和频率偏差均值的积,当ACE×ΔF<0时表明控制策略对系统频率恢复有利,反之不利。由于置信水平越高,系统允许承受的价格水平也越高,即对风险厌恶程度越低,对于控制区而言,可以调度的AGC机组数量也就越多,趋向于通过增加内部AGC机组的下令来实现区域供需平衡,且尽可能减少联络线功率的吸收,从而最大限度地实现对外部系统的功率支援。计算结果表明,99%置信水平下的区域控制偏差比95%置信水平下的小,表明置信水平越高,控制效果越好。同时,99%置信水平下ACE×ΔF<0的考核点比95%置信水平下的多,表明置信水平越高,越有利于系统频率的恢复。

图7 ACE趋势图Fig.7 Trends of ACE

图8 ACE×ΔF趋势图Fig.8 Trends of ACE×ΔF
(2) 联络线功率偏差。
图9为联络线功率偏差趋势图。联络线功率偏差大于0,表明系统对外部系统支援,或者从外部系统少吸收功率,反之则从外部系统多吸收功率。计算结果表明,99%置信水平下,联络线功率偏差在大部分情况下均大于0,对系统的支援力度更大,更有利于系统频率的稳定。

图9 联络线功率偏差趋势图Fig.9 Trends of tie-line’s power deviation
(3) 机组下令。
图10为AGC下令值。结果显示:99%置信水平下的机组下令次数比95%置信水平下的多,且下令功率总量也更大,表明置信水平越高,控制成本越大。
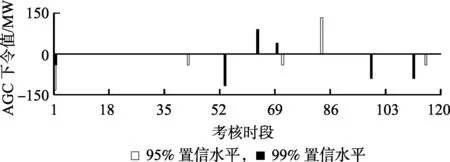
图10 AGC下令值Fig.10 Values of AGC order
根据以上分析,在保障CPS考核指标合格的前提下,置信水平越高,控制区的AGC机组下令次数更多,同时下令值也越大,控制成本越高,但置信水平越高,越有利于系统频率稳定。电力系统实际运行时,电网企业可综合考虑机组的市场报价、调节性能等因素选择恰当的置信水平。
4 结论
本文引入度量市场风险的VaR方法,构建了考虑市场力风险约束的最优AGC控制模型,解决了传统AGC优化模型难以考虑市场力风险的问题。通过理论和仿真分析,得到以下结论。
a. 置信水平越高,AGC机组的下令次数越多,下令值越大,控制成本也越高,但控制效果会更好,更有利于系统频率的恢复。反之,置信水平越低,AGC机组的下令次数及下令值相应减少,控制成本降低,但控制效果变差,不利于系统频率质量的改善。
b. 在满足CPS考核指标前提下,可通过适当调节置信水平来实现对互联系统的支援力度。置信水平越高,对外支援的力度越大,越有利于系统安全运行,但付出的调节成本越高。
c. 在电网实际运行中,为控制系统调节成本,满足CPS指标考核的要求,电网企业可以综合考虑机组市场报价、调节性能等因素,适当调节风险置信水平,实现风险与成本的均衡。
参考文献:
[1] 中共中央,国务院. 关于进一步深化电力体制改革的若干意见(中发〔2015〕9)[Z]. 2015.
[2] BJORGANR,LIU C C,LAWARREE J. Financial risk management in a competitive electricity market[J]. IEEE Transactions on Power Systems,1999,14(4):1285-1291.
[3] JALEELI N,VANSLYCK L S. NERC’s new control performance standards[J]. IEEE Transactions on Power Systems,1999,14(3):1092-1099.
[4] 赵万宗,李滨,韦化,等. 互联电网CPS标准下计及一次调频的最优AGC控制模型[J]. 中国电机工程学报,2016,36(10):2656-2664.
ZHAO Wanzong,LI Bin,WEI Hua,et al. The optimal AGC control strategy considering the primary frequency regulation under the control performance standard for the interconnected power grid[J]. Proceedings of the CSEE,2016,36(10):2656-2664.
[5] 李卫东,常烨骙,陈兆庆,等. 区域控制偏差的动态内涵[J]. 电力系统自动化,2016,40(24):146-150,163.
LI Weidong,CHANG Yekui,CHEN Zhaoqing,et al. Dynamic contents of area control error[J]. Automation of Electric Power Systems,2016,40(24):146-150,163.
[6] 翁毅选,邓长虹,黄文涛,等. 基于统计理论的含风电互联电网CPS研究[J]. 电力自动化设备,2013,33(12):79-84.
WENG Yixuan,DENG Changhong,HUANG Wentao,et al. Research of CPS based on statistical theory for interconnected power grid with wind power[J]. Electric Power Automation Equipment,2013,33(12):79-84.
[7] 巴宇,刘娆,李卫东. CPS及其考核在北美与国内的应用比较[J]. 电力系统自动化,2012,36(15):63-72.
BA Yu,LIU Rao,LI Weidong. Comparison of CPS and its assessment between North America and China[J]. Automation of Electric Power Systems,2012,36(15):63-72.
[8] YU Tao,ZHOU Bin,CHAN K W. Stochastic optimal relaxed automatic generation control in non-Markov environment based on multi-step Q(λ) learning[J].IEEE Transactions on Power Systems,2011,26(3):1272-1282.
[9] 杨方,孙元章,程林. 计及稳定断面安全的AGC协调控制[J]. 电力自动化设备,2010,30(8):13-18.
YANG Fang,SUN Yuanzhang,CHENG Lin. Coordinated automatic generation control with voltage security constraints for interconnected power grids[J]. Electric Power Automation Equipment,2010,30(8):13-18.
[10] 刘奇,刘斌,余涛. 基于CPS统计特性的自适应自动发电控制策略[J]. 电力自动化设备,2010,30(12):74-78.
LIU Qi,LIU Bin,YU Tao. Adaptive AGC strategy based on statistical property of CPS[J]. Electric Power Automation Equipment,2010,30(12):74-78.
[11] 李滨,韦化,农蔚涛,等. 基于现代内点理论的互联电网控制性能评价标准下的AGC控制策略[J]. 中国电机工程学报,2008,28(25):56-61.
LI Bin,WEI Hua,NONG Weitao,et al. AGC control strategy under control performance standard for interconnected power grid based on optimization theory[J]. Proceedings of the CSEE,2008,28(25):56-61.
[12] 余涛,张水平. 在策略SARSA算法在互联电网CPS最优控制中的应用[J]. 电力系统保护与控制,2013,41(1):211-216.
YU Tao,ZHANG Shuiping. Optimal CPS control for interconnected power systems based on SARSA on-policy learning algorithm[J].Power System Protection and Control,2013,41(1):211-216.
[13] 付蓉,王蓓蓓,李扬,等. 输电网络约束下发电商的市场力行为分析[J]. 电力自动化设备,2008,28(5):6-11.
FU Rong,WANG Beibei,LI Yang,et al. Analysis of market power behavior of electricity suppliers under network constraints[J]. Electric Power Automation Equipment,2008,28(5):6-11.
[14] 李晓刚,李玉平. 统一出清电价下发电厂商的持留容量行为及相关抑制措施[J]. 电力自动化设备,2004,24(7):85-88.
LI Xiaogang,LI Yuping. Withholding generation capacity and mitigation mechanism of market power under uniform clearing pricing method[J]. Electric Power Automation Equipment,2004,24(7):85-88.
[15] SMITHSONC,MINTON L. Value at risk[J]. Risk,1996,9(1):25-27.
[16] 杨力俊,郭联哲,谭忠富. 几种发电商市场力评估指标的对比分析[J]. 电网技术,2005,29(2):28-33.
YANG Lijun,GUO Lianzhe,TAN Zhongfu. Comparison and analysis of several market power assessment indices for power generation company[J]. Power System Technology,2005,29(2):28-33.
[17] OSTROWSKI J,ANJOS M F,VANNELLI A. Tight mixed integer linear programming formulations for the unit commitment problem[J]. IEEE Transactions on Power Systems,2012,27(1):39-46.
[18] 盛骤,谢式千,潘承毅. 概率论与数理统计[M]. 4版. 北京:高等教育出版社,2008:161-171.

