某飞机机头改装过渡段强度及振动特性分析

鲜章林， 李思潭

（中国飞行试验研究院改装部，西安 710089)

0 引言

为了对航空设备的最终性能进行评估，需要对设备进行飞行试验。在试飞评估中，必须将被试航空设备装载到飞机的特定位置以满足被试设备的实验要求，除了在飞机外挂吊舱加载被试设备外，最典型的加载方式是对载机进行改装，将设备布置到飞机理论外形之内，以避免外挂物对载机气动外形的影响，从而导致飞行性能的降低，以此保证被试设备的特殊测试要求。

本文以某飞机机头加载被试设备为研究对象，利用三维设计软件CATIA对该机机头过渡段进行几何建模，运用有限元素法建立结构的有限元模型，并进行典型工况的静强度分析，获得结构的应力分布及变形结果，并对各零部件进行强度校核以验证改装过渡段强度满足设计要求；采用Lanczos模态分析法[1]获得结构的模态频率和形状，并结合空速管Karman涡街[2]分离频率和发动机转动频率对机头过渡段进行振动特性分析。

1 有限元建模

1.1 结构简介

整个机头过渡段分为前过渡段和后过渡段，两过渡段通过对接框进行连接。后过渡段利用原机结构在截断面处设计对接框，并在相应连接区域进行加强；前过渡段根据原机气动外形重新设计，其总体结构与原机过渡段类似。纵向构件包括上下腹板和短梁，横向构件包括对接框和半框等，两侧设计维护口盖，上下腹板梁盒式结构中的梁、腹板位置与原机腹板梁结构对应；前过渡段前段为机头罩，在机头罩后方加装空速管。改装机加件材料采用7050-T7451，改装型材材料采用LY12-CZ，光学玻璃材料为CVDZnS，雷达罩材料为F.B-2-25，

图1 过渡段总体框架结构

图2 空速管结构

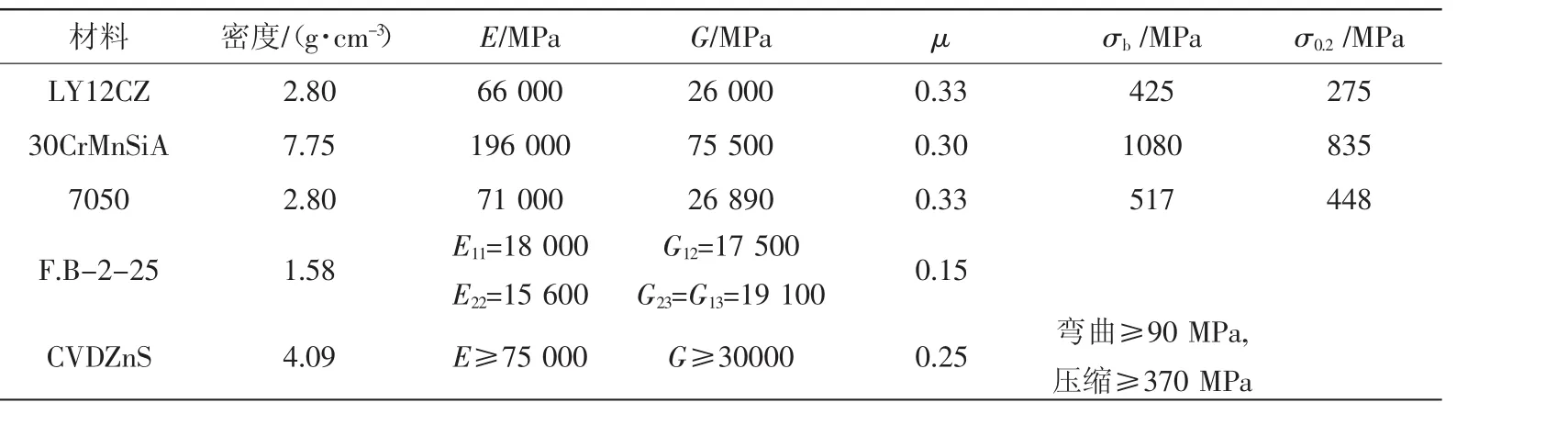
表1 主要材料力学参数

过渡段总体框架结构如图1所示，空速管结构如图2所示，主要材料的力学性能如表1所示。

1.2 有限元建模

依据过渡段CATIA数模，分析整个结构的传力路径，根据各结构件的传力特性和圣维南原理将各个结构件进行力学简化：将蒙皮、框腹板、口盖腹板、梁腹板、转接支架等简化为二维壳单元（CQUAD4，CTRIA3）；将加强筋、梁缘条、型材简化为一维梁单元（CBAR）；将空速管及其连接结构简化为三维体单元（CTETRA，CHEXA，CPENTA）；将舱内加装设备简化为集中质量单元（CONM2）；将螺栓类连接件简化为刚性单元（RBE2）单元；铆钉连接通过连接结构节点耦合进行模拟。整个有限元模型单元数据统计如表2所示，有限元模型如图3～图4所示。

表2 有限元模型单元统计

图3 过渡段结构有限元模型

图4 空速管及其连接结构有限元模型

1.3 约束及载荷

将机头过渡段与机身连接处进行固支，根据该飞机的飞行包线选取严重工况进行静强度校核，并进行整个机头过渡段的模态分析。对于空速管的模态分析，将空速管与机头过渡段连接处进行固支。

由于加装设备通过集中质量进行模拟，因此过渡段的载荷主要为惯性载荷和气动载荷。惯性载荷以过载的形式进行施加，气动载荷利用CFD软件计算得到相应工况的压力分布，并用Inverse-distance插值方法将气动压力插值到结构网格上。根据该飞机的飞行包线确定严重工况如下：马赫数1.06，飞行迎角6.00°，法向过载10.50。

2 强度计算结果与分析

2.1 变形分析

为了保证结构刚度足够以满足飞行安全，以及试飞过程中设备的测量精度，本文计算了在上述极限载荷下的变形结果，图5给出了过渡段整体变形云图，图6给出了过渡段内部结构变形云图。可见整个过渡段结构变形连续合理，最大位移发生在空速管顶部为14.50 mm，内部仪器安装支架变形小于1.00 mm，变形结果不会影响飞行安全和被试设备试验精度。

图5 过渡段整体变形云图

图6 过渡段内部结构变形云图

2.2 强度分析

高速大过载工况下，结构强度对飞行安全至关重要，根据有限元分析结果可知，过渡段在对接框处产生较大应力从而导致其安全系数最小，这是因为前后过渡段在对接框处通过18套M10螺栓连接，传力路线在对接框处发生改变。图7给了该极限工况下的对接框的等效应力云图，从图中可以看到最大等效应力为289.00 MPa，安全系数为1.79。

图7 对接框等效应力云图

图8 空速管等效应力云图

前置杆外伸长度约2000 mm，在较大过载时，该双支点外伸悬臂梁将在根部产生较大的应力，图8给出了该极限工况下前置杆等效应力云图，从图中可以看到最大等效应力为52.40 MPa，安全系数为9.87。

由以上分析结果可知，该机头过渡段结构设计合理，传力路线明确，各结构件、连接件强度满足相关要求。

3 动力学特性分析

飞机飞行过程中结构失效的主要原因，除了由于在静载作用下导致结构应力超过其极限应力，还有很大一部分是在动载荷作用下由于结构固有动力学特性不合理而产生局部共振，从而使振动发散最终导致结构破坏。不同于疲劳破坏的发生需要经历一定的载荷循环次数，并且具有典型的疲劳裂纹扩展过程，由共振导致的结构破坏往往是由于在某一次飞行架次中达到一定的条件时产生快速而极具破坏性的损伤，导致结构迅速破坏或解体，因此改装结构的动力学特性分析就显得极为重要。

3.1 固有频率计算

结构刚度和质量分布将严重影响结构的固有频率计算结果，为保证结构刚度和质量模拟的准确性，选取实际结构截面作为梁单元截面，并通过单元偏置实现所定义的梁截面同实际结构截面位置的重合；通过在非结构部件重心处的集中质量单元来对非结构部件进行模拟，以实现质量分布的等效，最终进行有限元模型总质量统计和与实际结构的对比，以此保证固有频率计算的准确性。

表3给出了由Lanczos方法计算得到的过渡段和空速管前五阶固有频率分布，从表中可以看出整个过渡段的前两阶模态形状主要以空速管变形体现，图9、图10给了整个过渡段前两阶模态形状。

3.2 空速管Karman涡街频率计算

飞机在定常飞行过程中，来流绕过空速管时会在空速管两侧周期性地脱落出旋转方向相反、排列规则的双列线涡，进而形成Karman涡街[3]。Karman涡街的频率作为一种外来激励频率将对飞机结构产生影响，为此有必要考量该涡街频率对结构共振的影响。

根据Karman涡街频率的计算公式：

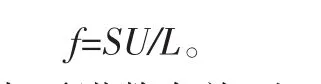
表3 过渡段和空速管前五阶固有频率分布 Hz

图9 过渡段一阶模态形状

图10 过渡段二阶模态形状

式中：S为无量纲参数，与雷诺数有关，由于该飞机的全包线范围内的典型状态的雷诺数分布在500≤Re≤10 000之内，S取0.2；L为圆柱的直径（本文取55 mm）；U为垂直于圆柱轴线的气流速度。

按照该公式根据载机飞行包线即可计算各个高度下的最小Karman涡街频率，表4给出了5 km高度以下的最小Karman涡街频率。

表4 Karman涡街频率表

3.3 发动机固有旋转频率计算

该飞机配装的发动机的低压转子100%转速为n=11156 r/min（185.93 r/s），高压转子100%转速为n=11 373 r/min（189.55r/s），常用状态下发动机旋转频率如表5所示。

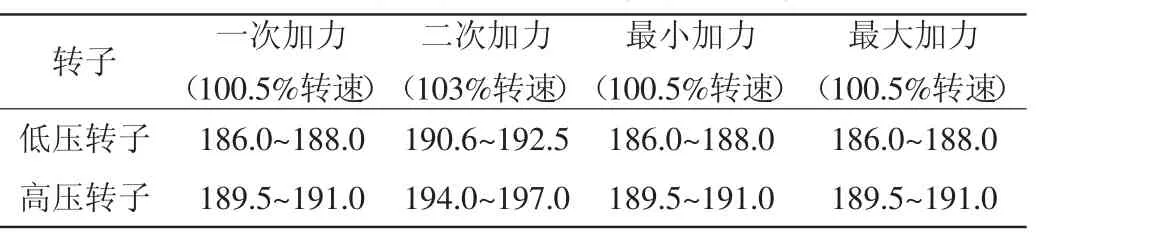
表5 常用状态下发动机旋转频率 Hz

3.4 过渡段动力学特性分析

以空速管Karman涡街频率和发动机旋转频率作为结构的激振频率，综合4.1～4.3节计算结果可以得到以下结论：1）空速管Karman涡街频率随着飞行高度增加而增加，其最小频率为26.61 Hz，高于过渡段和空速管的前两阶频率，因此结构不会与空速管Karman涡街频率发生耦合。2）发动机高压、低压转子在各典型工作状态下的旋转频率均远离结构的主要固有频率，因此结构不

会与发动机旋转频率发生耦合。

4 结语

本文针对某飞机设计了机头过渡段结构，利用有限元法对某飞机机头过渡段进行建模，并计算极限工况下结构的变形和应力分布，进行了静强度校核；利用Lanczos方法计算过渡段和空速管的固有频率，在计算空速管涡街分离频率和发动机旋转频率的基础上对过渡段的共振特性进行了分析。

通过计算分析得到了机头过渡段的强度校核结果及振动特性，计算结果表明，该对接框式机头过渡段可以满足结构强度、刚度要求，结构的共振特性良好，此结构形式可以为后续飞机改装提供参考。

［参考文献］

[1] 吴立昕.求解大型稀疏对称矩阵广义特征值问题的Lanczos方法及通用程序[J].振动与冲击,1987(3):19-27.

[2] 武作兵,凌国灿.Karman涡街流场的定性分析研究[J].空气动力学学报,1994,12(3):355-362.

[3] 何子华.某飞机机身加装外挂后静力试验初步方案设计[D].西安:西北工业大学,2007.

[4] 刘亚奇,胡锦旋,刘星北,等.翼下发动机吊架及其与机翼连接结构研究[J].民用飞机设计与研究,2009(增刊1):74-76.

[5] 刘文莉.结构试验载荷设计自动化方法研究[D].西安:西北工业大学,2001.

[6] 李书,王波,胡继忠.基于Lanczos方法的结构动力学灵敏度分析[J].应用数学和力学,2003,24(1):83-88.

[7] 郭建.飞机复合材料整流罩结构静强度分析[J].科学与财富,2015(19):369.

[8] 白金泽,孙秦,郭英男.应用ANSYS进行复杂结构应力分析[J].机械科学与技术,2003,22(3):441-443.

[9] 田智亮,孙秦.复合材料加筋筒段压载荷承载能力优化[J].航空工程进展,2014(3):377-382.

[10]沈真,杨胜春.飞机结构用复合材料的力学性能要求[J].材料工程,2007(增刊1):248-252.

[11] 纪学,孙秦,高扬.大型薄壁壳体结构动力学响应特性的数值模拟[J].机械强度,2011,33(5):782-785.

[12] 中国航空研究院.复合材料结构稳定性分析指南[M].北京:航空工业出版社,2002.

[13]军用飞机复合材料强度验证要求:HB7491-1997[S].

[14]辜蕾钢.铝合金厚板预拉伸及淬透性研究[D].重庆:重庆大学,2004.

[15]楼瑞祥.大飞机用铝合金的现状与发展趋势[C]//大型飞机关键技术高层论坛暨中国航空学会2007年学术年会论文集.2007.