基于PEST的HSPF模型径流模拟优化

杨 博，陈 莹，2，3†，陈兴伟，2，3，刘梅冰，2，3，高 路，2，3

(1.福建师范大学地理科学学院，350007，福州；2.湿润亚热带山地生态国家重点实验室培育基地，350007，福州；3.福建省陆地灾害监测评估工程技术研究中心，350007，福州)

地表径流是造成土壤侵蚀的主要原因之一[1]。近年来，由于气候变化和人类活动的影响，流域水循环和水资源问题趋于复杂化。水文模型是对自然界中复杂水文现象的近似模拟[2]，可以实现流域径流定量化研究，是水文科学研究的一种手段和方法。HSPF模型是半分布式水文模型的优秀代表，在水文过程模拟、气候与土地利用变化的水文响应研究等方面得到了广泛应用[3]。参数率定是水文模拟中不可避免的重要环节[4]。目前HSPF模型主要通过GA (Genetic Algorithm)[5]、SCE(Shuffled Complex Evolution Algorithm)[6]、GLUE(Generalized Likelihood Uncertainty Estimation)[7]以及人工率定等方法，且主要基于单目标函数实现参数的率定。PEST(Parameter Estimation)自动率定程序是由Doherty博士基于GML(Gauss-Marquardt-Levenberg)算法开发的，其具有逆海森方法和最速下降法的优点，可以通过较少的模型运行次数，得到最优的参数结果[8]。此外，与其他自动率定方法相比，PEST对建模者编程能力的要求较低，不需要通过编写代码即可实现水文模型和优化算法间的耦合，且基于WINDOWS平台运行的特性让操作简单易行，已在地下水模型中广泛应用[9-10]。目前，基于PEST实现HSPF模型多目标函数率定的相关研究较少[11]，且在率定中多侧重于洪水流量，对枯水的关注不足；因此，本研究以山美水库流域为例，将PEST应用于HSPF模型中，开展单目标与多目标率定的对比研究，并根据丰水期和枯水期对多目标率定的目标函数进行优化，分析其对径流模拟的影响，为流域水文模型的参数率定提供参考。

1 研究区概况

山美水库流域位于福建省晋江流域的东北部(E 118°3′～180°30′，N 25°9′～25°32′)，海拔在60～1 360 m之间，流域面积1 023 km2，占晋江流域总面积的18.2%。流域属于亚热带季风气候，年均温约为20.9，年降水量约为1 600 mm，干湿季分明，降水空间分布上自西北向东南逐渐减少。在土地利用方面，研究区主要以林地为主(64.4%)，其次为园地(14.3%)、耕地(12.1%)、建设用地(5.1%)、水域(2.2%)、未利用地(1.1%)和草地(0.8%)。

2 研究方法

2.1 数据来源

HSPF模型的构建需要涉及气象、水文、DEM和土地利用等数据。笔者使用的气象数据包括2001—2010年永春、德化2个气象站日最高气温、最低气温、相对湿度和风速数据，以及15个雨量站日降雨量数据；水文数据包括2001—2010年山美水库日入库、出库流量和龙门滩月调水数据；DEM数据分辨率为30 m×30 m，从“中国科学院国际科学数据服务平台”获得；土地利用数据来自山美水库2006年TM遥感影像的解译，共划分水域、草地、未利用地、建设用地、耕地、园地和林地7种类型。

2.2 HSPF模型简介

HSPF是由美国国家环境保护局于1981年开发的，采用Fortran语言编写的半分布式综合流域模型。模型由透水地段水文水质模拟模块(PERLND)、不透水地段水文水质模拟模块(IMPLND)以及地表水体模拟模块(RCHRES)3部分组成[12]。

2.3 PEST简介与模型率定

PEST自动率定是模型文件输入、输出与用户交互的过程，通过时间序列处理程序TSPROC提取HSPF模型的输入与输出文件，使用非线性评价方法GML进行迭代运算，得到参数之后代入HSPF模型进行模拟，直至满足迭代终止条件，获得最优参数结果[13]。

PEST的目标函数主要涉及了不同时间尺度的径流总量、各种流量组分(基流、洪峰)和不同频率流量保证率的模拟效果[14]，笔者选择日流量偏差、月流量偏差和1%、5%、10%、25%、50%、75%、90%、95%超流量天数偏差作为目标函数，公式如下：

(1)

(2)

(3)

式中：f1(θ)、f2(θ)、f3(θ)分别为日流量、月流量、超流量天数偏差的目标函数；Qi和Q′i为日流量的实测值和模拟值；Ei和E′i为日流量实测值和模拟值中超过某一流量值的时间，d；n为模拟时间，d；Ny为模拟月数，Ny=12；n为每月的时间，d；Ec为模拟的超流量天数类型数量；θ为率定参数集；w为目标函数权重。

针对率定中对枯水流量考虑的不足，本研究对日流量偏差f1(θ)这一目标函数进行改进，将时间序列划分为丰水期(4—6月)和枯水期(11月—翌年3月)，f4(θ)和f5(θ)分别计算丰水期和枯水期的日流量偏差，公式如下：

(4)

(5)

式中：na为丰水期模拟时间，d；nb为枯水期模拟时间，d。

笔者选择日流量偏差，即将f1(θ)作为单目标率定的目标函数；F1(θ)和F2(θ)作为2个多目标率定的目标函数，具体公式如下：

F1(θ)=f1(θ)+f2(θ)+f3(θ)；

(6)

F2(θ)=f2(θ)+f3(θ)+f4(θ)+f5(θ)。

(7)

多目标函数设置不同的权重会直接影响率定结果，应保证各目标函数的偏差在同一个数量级内，本研究将权重设置为各目标函数初始偏差的倒数[15]。为下文方便，本文将基于F1(θ)和F2(θ)多目标函数的分析结果分别称为多目标和多目标(丰枯)的率定结果。

笔者将2001—2005年作为模型的率定期，2006—2010年为验证期，并选取纳什效率系数NSE、决定系数R2、均方根误差RMSE和比例偏差PBIAS对模型日、月径流的模拟结果进行评估。其中NSE和R2表示径流模拟的拟合程度，RMSE和PBIAS均反映模拟值与实测值的偏差。一般认为，若0.50.75为优秀，R2与NSE相同，PBIAS<10%为优秀，10%≤PBIAS<15%为良好，若PBIAS为负值则相反[16]。

3 结果与分析

3.1 参数敏感性分析与参数率定

参考相关研究确定研究区相关模型参数的率定范围[17]，采用Morris筛选法[18]对参数进行敏感性分析，并选取NSE作为评价指标，筛选出9个敏感参数(表1)。

3.2 模拟结果比较

3.2.1 基于单目标函数与多目标函数参数率定的模拟结果比较 从日径流模拟结果(表2)来看，在率定期，就R2而言，单目标和多目标率定的结果相差不大；就NSE、RMSE和PBIAS而言，基于多目标率定的结果更优。单目标率定的NSE为0.70，2个多目标率定的NSE均达到0.79，表明2个多目标率定的结果对日径流过程的拟合程度更优。单目标率定的RMSE为32.85 m3/s，2个多目标率定分别为27.56和27.42 m3/s，单目标率定的PBIAS为-28.4%，2个多目标率定分别为-6.92%和-6.65%，显然，多目标率定可以有效降低日径流模拟值与实测值的偏差。此外，验证期结论与率定期相同，多目标率定的日径流模拟结果更优。

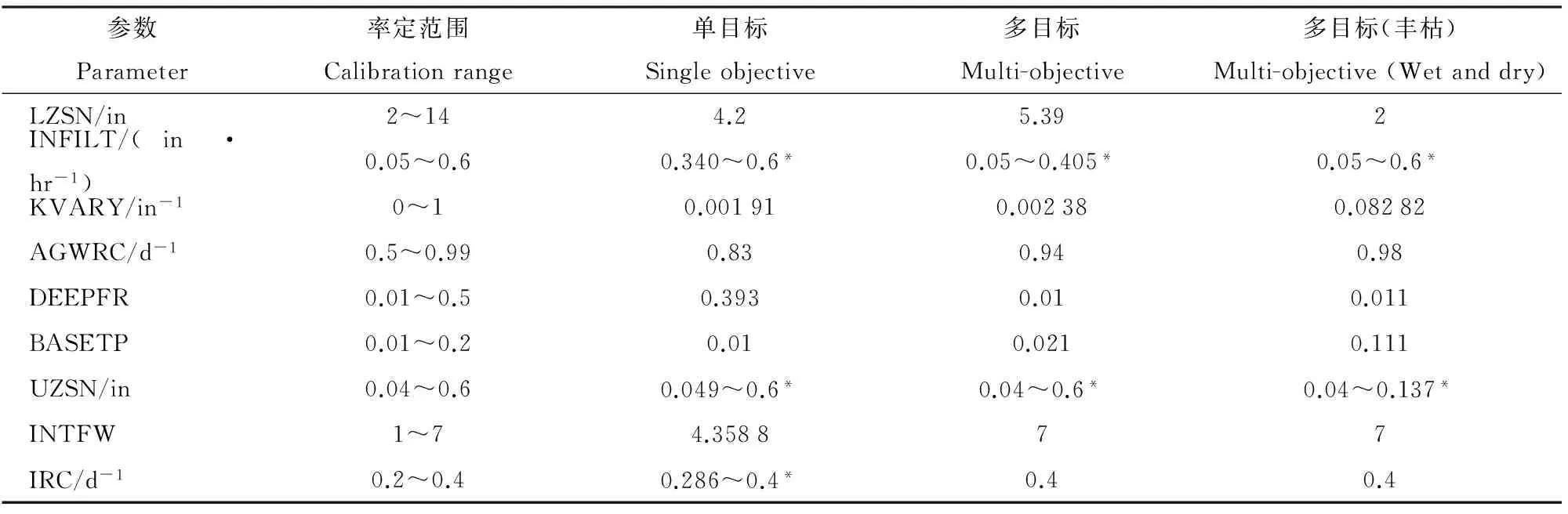
表1 单目标与多目标函数的参数率定结果Tab.1 Estimated parameter values by calibration based on single objective or multi-objective functions

注：参数使用英制单位。LZSN为额定的下土壤层蓄积；INFILT为土壤渗透率；KVARY为地下水退水系数影响因子；AGWRC为地下水退水系数；DEEPFR为深层地下水入渗系数；BASETP为基流蒸散发系数；UZSN为额定的上土壤层蓄积；INTFW为壤中流入渗系数；IRC为壤中流退水系数。*随土地利用类型变化取值不同。Notes: Parameters use imperial units. LZSN is lower zone nominal storage. INFILT is soil infiltration capacity index. KVARY is a parameter of affecting the behavior of groundwater recession flow. AGWRC is groundwater recession coefficient. DEEPFR is fraction of groundwater inflow lost to deep groundwater. BASETP is fraction of potential ET that can be satisfied from base flow. UZSN is upper zone nominal storage. INTFW is interflow inflow parameter. IRC is interflow recession parameter.*indicates that value varies with the change of land use type.

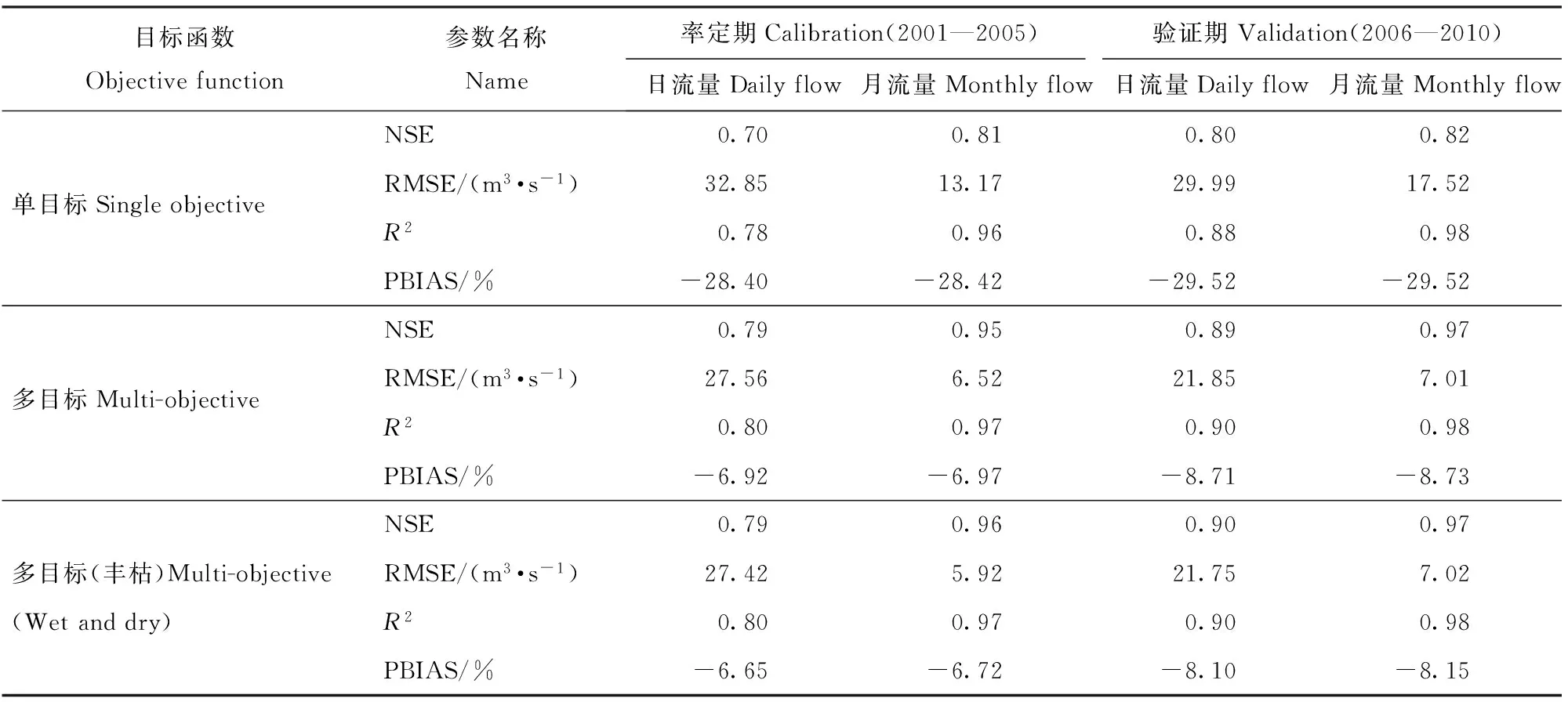
表2 单目标与多目标率定的日、月径流过程拟合优度结果Tab.2 Goodness-of-fit of single objective and multi-objective calibration for daily and monthly flows

注：NSE为纳什效率系数；RMSE为均方根误差；PBIAS为比例偏差。Notes: NSE is Nash-Sutcliffe efficiency coefficient. RMSE is root mean square error. PBIAS is percent bias.

从月径流模拟结果来看(表2)，NSE、RMSE、R2和PBIAS等4个评价指标的结果与日径流的结论一致，相比单目标率定，2个多目标率定的NSE和R2数值提高，RMSE和PBIAS数值降低，说明2个多目标率定的月径流拟合程度更优，模拟值与实测值的偏差更小。从月径流过程(图1)也可见，相对于多目标率定而言，单目标率定的月径流对实测值存在更大程度的低估，对径流总量和变化趋势的模拟较差。此外，基于多目标与多目标(丰枯)率定的月径流模拟结果存在差异，并且差异主要出现在枯水期。

从流量历时曲线(图2)来看，较单目标率定而言，2个多目标率定的FDC曲线整体拟合程度更优，且在低流量部分模拟结果提高的更为显著。为进一步比较各目标函数率定的模拟结果，以Q10、Q50和Q90等流量特征值为代表，统计模拟值与实测值的PBIAS(表3)。单目标率定的Q10、Q50和Q90的PBIAS在率定期分别为-21.40 %、-25.25%和-54.51%，验证期分别为-30.81%、-23.21%和-43.39%，与实测值相差较大；而多目标率定由于考虑了不同频率的超流量天数偏差，其Q10、Q50和Q90的PBIAS均显著降低，更接近实测值，但Q90仍存在较大的偏差。此外，2个多目标率定的模拟结果也存在较大差异。较多目标率定而言，虽然多目标(丰枯)率定的Q10偏差有所提高，但是Q90的偏差却显著降低，率定期和验证期的PBIAS结果分别从-45.39%和-32.86%提高到-27.03%和-13.20%。显然，多目标(丰枯)率定更能捕捉到低流量的流量特征，可以显著减小枯水流量模拟值与实测值的偏差。

图1 单目标与多目标率定的月流量模拟结果Fig.1 Observed and simulated monthly flows of single objective and multi-objective calibration

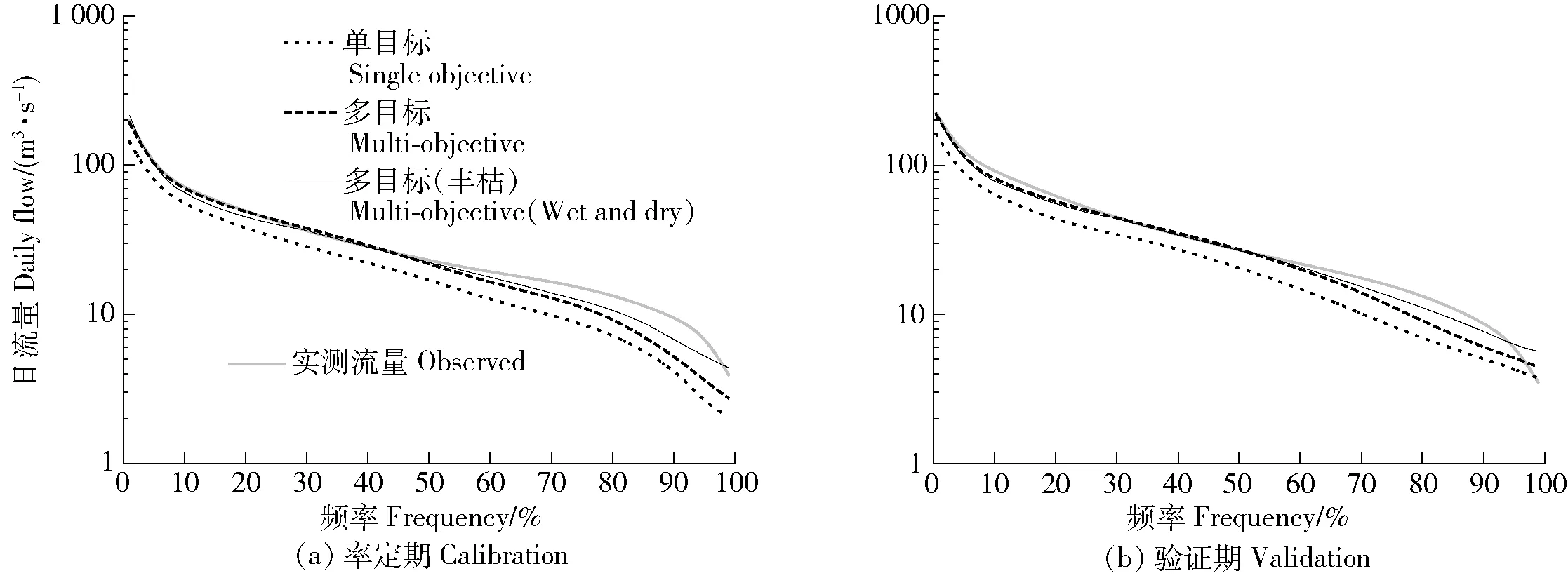
图2 单目标与多目标率定期(a)与验证期(b)日流量曲线模拟结果Fig.2 Flow duration curves of single and multi-objective calibration in (a) calibration and (b) validation period

3.2.2 基于2个多目标函数参数率定的模拟结果比较 针对多目标与多目标(丰枯)率定流量特征值的差异，进一步采用区分丰、枯水期的方式，分析比较2个多目标函数的率定结果。

从丰水期的日、月径流模拟结果(表4)来看，相比多目标(丰枯)率定，多目标率定的RMSE和PBIAS取得了更好的模拟效果，但是两者在数值上差别较小。同时，从丰水期的月径流过程(图1)也可以看出，多目标与多目标(丰枯)率定的月径流过程差别不显著。

从枯水期日径流的模拟结果(表4)来看，在率定期，相比多目标率定，多目标(丰枯)率定的NSE和R2分别从-0.04提高到0.25、从0.37提高到0.47，说明多目标(丰枯)率定的日径流拟合效果更优；就RMSE和PBIAS而言，相比多目标率定，多目标(丰枯)率定RMSE从9.54降低到8.06 m3/s，PBIAS从-33.57%提高到-24.52%，日径流模拟值与实测值的偏差降低。验证期的结论与率定期相同，相比多目标率定，多目标(丰枯)率定的NSE和R2提高，而RMSE和PBIAS降低。以率定期的枯水期日径流过程为例(图3)，多目标率定明显低估了枯水流量，对枯水期径流的模拟较差；而多目标(丰枯)率定可以捕捉到枯水的流量特征，缩小了模拟值与实测值的差距。月径流NSE、RMSE、R2、PBIAS的结果(表4)与日径流相同，即划分了丰水期和枯水期之后，HSPF模型月径流拟合程度和流量偏差均得到优化。从枯水期的月径流过程(图1)也可以看出，相比于多目标率定，多目标(丰枯)率定对于枯水期月径流也有一个更好的把握，拟合效果更优。

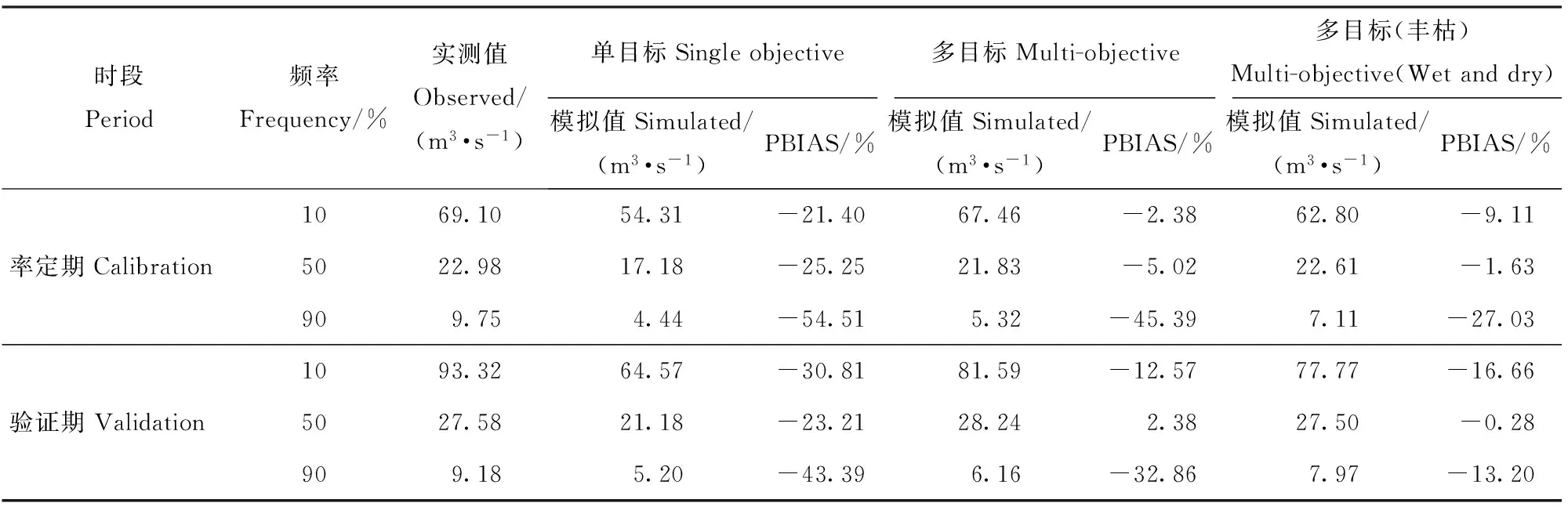
表3 单目标与多目标率定的日流量不同频率的PBIAS结果Tab.3 PBIAS of daily flow using single objective and multi-objective calibration at different frequencies

表4 2种多目标率定的丰水期与枯水期日、月径流过程拟合优度结果Tab.4 Goodness-of-fit of two multi-objective calibration approaches for daily and monthly flows during wet and dry seasons

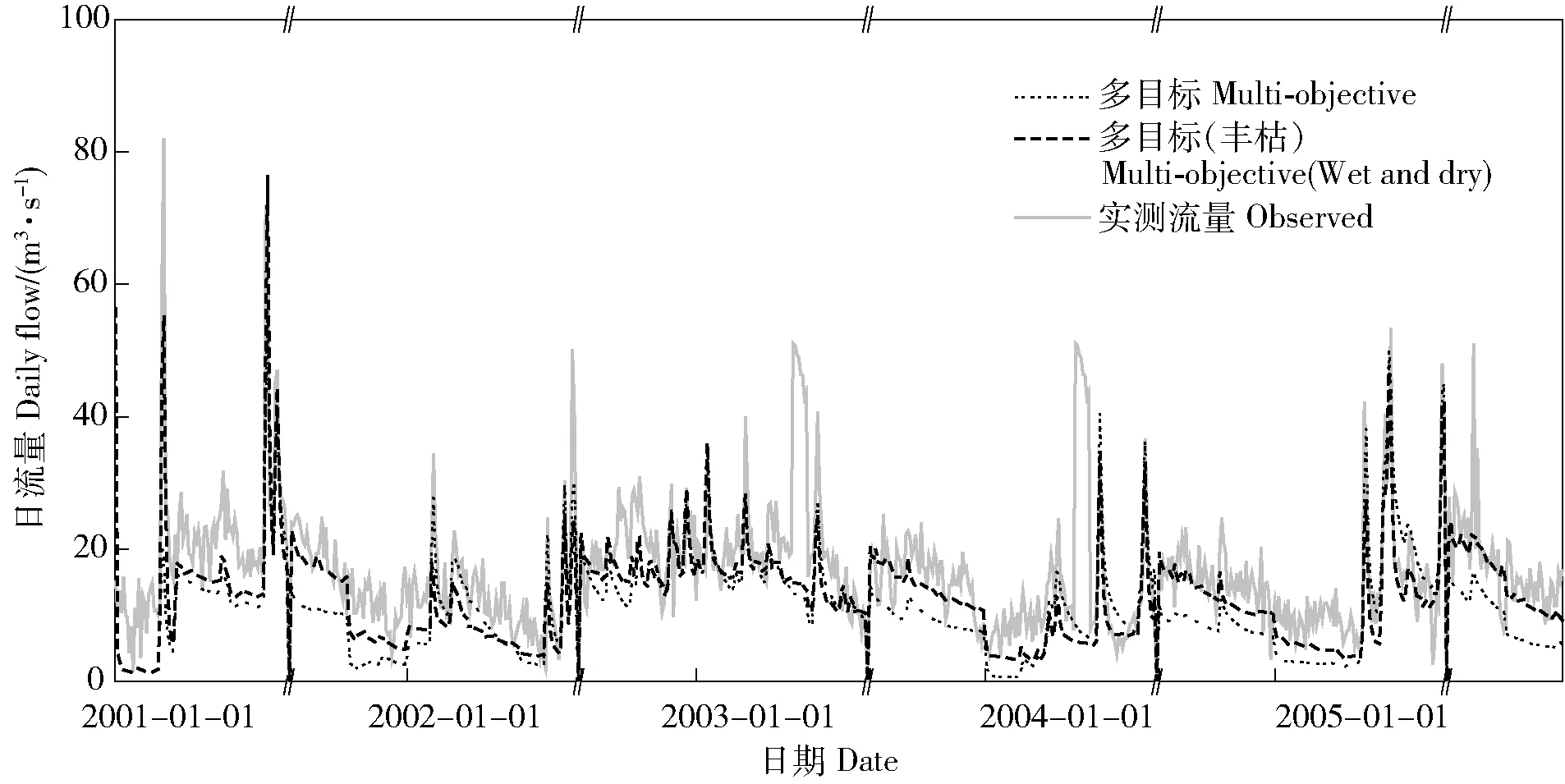
图3 2种多目标率定的2001—2005年枯水期日径流模拟结果Fig.3 Simulated daily flows of two multi-objective calibration approaches during dry season from 2001 to 2005

4 结论

1)在水文模型自动率定中，目标函数对模拟结果具有很大影响。相比仅采用日流量偏差的单目标率定，使用日流量、月流量和超流量天数偏差作为目标函数的多目标率定在日、月径流变化趋势、径流总量和不同频率的流量保证率偏差等方面均具有更好的模拟效果；因此，多目标率定综合了不同目标函数的特点，对不同的流量特征均具有较好的模拟效果。

2)以日流量、月流量和超流量天数偏差作为目标函数的多目标率定，虽然整体模拟效果已经较好，但是对枯水的模拟较差，率定期和验证期的PBIAS分别达到了-33.57%和-22.72%。而将日流量偏差划分丰、枯水期之后，枯水期日流量偏差作为1个单独的目标函数独立出来，并通过权重将4个目标函数设置在同一个数量级内，进而弥补了传统多目标率定忽视枯水流量的不足，显著提高了枯水期日、月径流的模拟效果。

同时，水文模型的参数率定是一个复杂的过程，今后仍需要对目标函数选择及权重设置深入研究，以提高模型的模拟精度及准确性。

[1] 程卓, YU B, 符素华. 黄土高原小区径流过程预测模型评价[J]. 中国水土保持科学, 2016, 14(6): 10.

CHENG Zhuo,YU B, FU Suhua. An assessment of runoff process-based models for plots in China Loess Plateau [J]. Science of Soil and Water Conservation, 2016, 14(6): 10.

[2] 金鑫, 郝振纯, 张金良. 水文模型研究进展及发展方向[J]. 水土保持研究, 2006, 13(4): 197.

JIN Xin, HAO Zhenchun, ZHANG Jinliang, Research evolution and development direction of hydrological models [J]. Research of Soil and Water Conservation, 2006, 13(4): 197.

[3] 李兆富, 刘红玉, 李燕. HSPF水文水质模型应用研究综述[J]. 环境科学, 2012, 33(7): 2217.

LI Zhaofu, LIU Hongyu, LI Yan.Review on HSPF model for simulation of hydrology and water quality processes [J]. Environmental Science, 2012, 33(7): 2217.

[4] 王中根, 夏军, 刘昌明, 等. 分布式水文模型的参数率定及敏感性分析探讨[J]. 自然资源学报, 2007, 22(4): 649.

WANG Zhonggen, XIA Jun, LIU Changming, et al. Comments on sensitivity analysis, calibration of distributed hydrological model [J]. Journal of Natural Resources,2007, 22(4): 649.

[5] CHO J H, LEE J H. Watershed model calibration framework developed using an influence coefficient algorithm and a genetic algorithm and analysis of pollutant discharge characteristics and load reduction in a TMDL planning area [J]. Journal of Environmental Management, 2015, 163(11): 2.

[6] SEONG C, HER Y, BENHAM B L. Automatic calibration tool for hydrologic simulation program-FORTRAN using a shuffled complex evolution algorithm [J]. Water, 2015, 7(2): 503.

[7] XIE Hua, LIAN Yanqing. Uncertainty-based evaluation and comparison of SWAT and HSPF applications to the Illinois River basin [J]. Journal of Hydrology, 2013, 481(2): 119.

[8] BAHREMAND A, DE SMEDT F. Distributed hydrological modeling and sensitivity analysis in Torysa Watershed, Slovakia [J]. Water Resources Management, 2008, 22(3): 393.

[9] MEYER S C, Lin Y F, ROADCAP G S. A hybrid framework for improving recharge and discharge estimation for a three-dimensional groundwater flow model [J]. Ground Water, 2012, 50(3): 457.

[10] KIM S M, BENHAM B L, BRANNAN K M, et al. Comparison of hydrologic calibration of HSPF using automatic and manual methods [J]. Water Resources Research, 2007, 43(1): W01402.

[11] EFSTRATIADIS A, KOUTSOYIANNIS D. One decade of multi-objective calibration approaches in hydrological modelling: A review [J]. Hydrological Sciences Journal-Journal des Sciences Hydrologiques, 2010, 55(1): 58.

[12] 韩莉, 刘素芳, 黄民生, 等. 基于HSPF模型的流域水文水质模拟研究进展[J]. 华东师范大学学报(自然科学版), 2015, 2015(2): 40.

HAN Li, LIU Sufang, HUANG Minsheng, et al. Review of simulation research in hydrology and water quality based on HSPF model [J]. Journal of East China Normal University (Natural Science), 2015, 2015(2): 40.

[13] DOHERTY J. PEST: model-independent parameter estimation, user manual part I: PEST, SENSAN and global optimizers [R]. Brisbane, Queensland. Australia: Watermark Numeric Computing, 2016: 108.

[14] 高伟, 周丰, 董延军, 等. 基于PEST的HSPF水文模型多目标自动校准研究[J]. 自然资源学报, 2014, 29(5): 859.

GAO Wei, ZHOU Feng, DONG Yanjun, et al. PEST-based multi-objective automatic calibration of hydrologic parameters for HSPF model [J]. Journal of Natural Resources, 2014, 29(5): 859.

[15] DOHERTY J, JOHNSTON J M. Methodologies for calibration and predictive analysis of a watershed model[J]. Journal of the American Water Resources Association, 2003, 39(2): 255.

[16] PARAJULI P B, NELSON N O, FREES L D, et al. Comparison of AnnAGNPS and SWAT model simulation results in USDA-CEAP agricultural watersheds in south-central Kansas [J]. Hydrological Processes, 2009, 23(5): 756.

[17] BALOCH M A, AMES D P, TANIK A. Hydrologic impacts of climate and land-use change on Namnam Stream in Koycegiz Watershed, Turkey [J]. International Journal of Environmental Science and Technology, 2015, 12(5): 1487.

[18] 高颖会, 沙晓军, 徐向阳, 等. 基于Morris的SWMM模型参数敏感性分析[J]. 水资源与水工程学报, 2016, 27(3): 89.

GAO Yinghui, SHA Xiaojun, XU Xiangyang, et al. Sensitivity analysis of SWMM model parameters based on Morris method [J]. Journal of Water Resources & Water Engineering, 2016, 27(3): 89.