蒙特卡罗法评定圆度测量不确定度
吴呼玲
(陕西国防工业职业技术学院机械工程学院,陕西 西安 710300)
0 引言
圆度误差是轴套类零件经常需要检测的形位误差项目。圆度误差测量不确定度的评定已成为测量领域的一个重要课题。常用的圆度测量不确定度评定方法有:①依据《测量不确定度表示指南》(guide to the expression of uncertainty in measurement,GUM)的基本原理和方法(GUM[1]法);②蒙特卡罗法[2](Monte Carlo method,MCM)。
GUM法需要根据评定方法建立误差数学模型,首先求出误差模型中的传递系数和参数间的相关系数,然后根据测量不确定度合成公式进行评定。由于圆度测量的点数较多,而且分为直角坐标系和极坐标系两种情况,误差模型较为复杂,因此很难求出不确定度。
蒙特卡罗法是一种统计模拟的方法,使用随机数模拟实际测量值来解决问题。该方法利用MATLAB软件中的相关函数产生一组随机数组来模拟实际测量值,求出形位误差的测量不确定度。该方法评定结果准确、操作方便、简单快捷,为测量技术领域和其他数据处理领域提供了新的方法。
1 圆度误差的最小二乘数学模型
测量圆度误差时,以零件测量时的回转中心O为圆心,选取两个相互垂直的径向线构成直角坐标系。圆度最小二乘模型如图1所示。
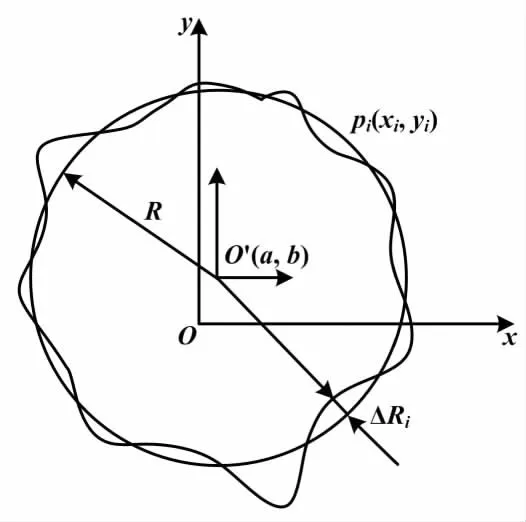
图1 圆度最小二乘模型Fig.1 The least squares model of roundness
在零件截面轮廓上,以等角度间隔进行测量采样。采样数据为pi(xi,yi)(i=1,2,…,n)。其中:xi为实际圆周上各采样点在x轴上的坐标值,yi为采样点在y坐标轴上的坐标值。设采样点的截面轮廓的最小二乘圆圆心O′的直角坐标为O′(a,b),最小二乘圆的半径为R,则最小二乘圆方程为:
(x-a)2+(y-b)2=R2
(1)
式中:a、b分别为最小二乘圆圆心在直角坐标系中的坐标值;R为最小二乘圆的半径。
根据实际轮廓圆上各pi点的直角坐标值,求得最小二乘圆圆心坐标a和b。
(2)
(3)
式中:n为实际轮廓等分的间隔数。
实际轮廓上的各采样点pi到最小二乘圆的偏距ΔRi为:
(4)
设距离最小二乘圆心最远的点和最近的点分别为(xM,yM)、(xL,yL),则圆度误差可表示为[3]:

(5)
式中:(xM,yM)为实际采样点距离最小二乘圆心最远的点坐标;(xL,yL)为实际采样点距离最小二乘圆心最近的点坐标。
2 圆度测量结果不确定度评定
2.1 GUM法
要计算圆度的测量不确定度[4],首先要确定圆度误差模型中各参数的传递系数和单点测量不确定度。
①计算式(5)中圆度误差模型各参数的传递系数[5]。
(6)
(7)
(8)
(9)

(10)

(11)
②计算各参数测量不确定度。
实际测量中,各测量点的测量环境是相同的,各点的测量不确定度也是相同的,都等于单点测量不确定度。a和b的不确定度可通过式(12)和式(13)求得:
(12)
(13)
式中:μ0为圆度的单点测量不确定度。
将推导出来的传递系数和单点测量不确定度代入
圆度测量不确定度评定公式[6],即可求得圆度的测量不确定度。
(14)
2.2 蒙特卡罗法
利用蒙特卡罗伪随机数原理,根据圆度误差模型,产生服从正态分布的随机数序列值。该序列值的期望为各参数的测量值,方差为各参数的单点标准不确定度,从而得出圆度的测量不确定度[7]。
①分析不确定度来源。设定分布类型、分布区间,得出各不确定度数值。
②确定圆度误差模型(5)中的参数:xM、xL、yM、yL、a、b的期望和方差。
③以xM、xL、yM、yL、a、b这6个参数的期望和方差,分别生成六维随机数模拟圆度误差的实际测量值,样本容量取M,对其进行圆度误差的不确定度评定。六维随机数分别为:[xM1,xM2,xM3,…,xMM];[xL1,xL2,xL3,…,xLM];[yM1,yM2,yM3,…,yMM];[yL1,yL2,yL3,…,yLM];[a1,a2,a3,…,aM];[b1,b2,b3,…,bM]。
④将产生的随机数值代入圆度误差模型,求出M个圆度误差值f。根据这组f值,构造概率分布。其方差值则为圆度误差的测量不确定度[8]。
3 试验数据采集及结果验证
使用爱德华公司MQ686型三坐标测量机,对JP19型万能工具显微镜的顶尖轴进行圆度误差的测量[9]和评定。将被测顶尖轴用高精度三爪卡盘夹紧,放置于三坐标测量机的测量平台上;然后对其进行圆度测量。在被测顶尖轴上选取三个截面,每个截面等角度测量24个点。三坐标测量机测量顶尖轴圆度数据如表1所示。

表1 顶尖轴圆度数据Tab 1 Roundness data of the top axismm
3.1 不确定度来源分析
三坐标测量机的工作要求是:室内温度达到20 ℃,被测零件和测量设备等温10 h。其三坐标测量机的不确定来源可忽略温度、湿度带来的影响,主要分析以下几个方面的影响[10]。
①重复性引起的不确定度分量。

4个点的测量不确定度结果分别为:
u1=σ1=0.028 μm;u5=σ5=0.032 μm;u15=σ15=0.023 μm;u20=σ20=0.035μm。
三坐标测量机重复性测量的不确定度u1=umax=0.035 μm。
②示值误差引入的不确定度分量。

③测量力引入的不确定度分量。
实际测量中,各部件的刚性较好,而且测量过程中测量力调节至很小,可忽略测力变形引起的误差。不确定度分量为u3=0。
④分辨力引入的不确定度分量。
⑤径向误差引入的不确定度分量。
三坐标的径向误差小于0.03 μm,服从均匀分布。
⑥温度引入的不确定度分量。
测量时,被测件、三坐标和测量人员都在等温后进行测量工作,而且符合国家标准要求的测量环境。不确定度分量u6=0。
因此,圆度单点测量不确定度为:
3.2 圆度误差计算
将表1中的测量结果代入式(2)和式(3),求出最小二乘圆的圆心坐标(a,b),可得最小二乘圆方程。其中:a=0.015 7、b=0.002 0。然后,求出各测点到最小二乘圆心的距离。各测点到最小二乘圆心计算结果如表2所示。

表2 各测点到最小二乘圆心的距离Tab.2 The distance between each measuring point to the least square center mm
测点和最小二乘圆如图2所示。

图2 测点和最小二乘圆示意图Fig.2 The measurement points and the least squares circle
由图2可知,距离圆心最远和最近的点分别是测点12和测点4(x轴的零度方向上的点序号为测点1,依次逆时针方向点的序号为2,3,…,24),对应的点坐标分别为xM=-9.670 3 mm、yM=-2.603 5 mm和xL=7.087 8 mm、yL=7.054 2 mm。将各参数代入式(3),则圆度误差值为:

3.3 计算不确定度
①GUM法评定圆度测量不确定度。

uf=2.274 μm
②蒙特卡罗法评定圆度测量不确定度。
利用计算机生成圆度误差模型中6个参数xM、xL、yM、yL、a、b的正态分布。每个参数数组的期望为该参数的测量值,方差为该参数的测量不确定度,即为:
[xM1,xM2,xM3,…,xMM]~N(-9.670 3 mm,1.56 μm)
[xL1,xL2,xL3,…,xLM]~N(7.087 8 mm,1.56 μm)
[yM1,yM2,yM3,…,yMM] ~N(2.603 5 mm,1.56 μm)
[yL1,xL2,xL3,…,xLM]~N(7.054 2 mm,1.56 μm)
[a1,a2,a3,…,aM]~N(0.015 7,0.318 μm)
[b1,b2,b3,…,bM]~N(0.002,0.318 μm)
取样本容量M=10 000。根据所得随机数,求出10 000个圆度误差值f,构建圆度误差概率分布。圆度误差概率分布直方图如图3所示。求出这组数据的期望和方差,即为圆度误差和圆度测量不确定度[12]。

图3 圆度误差概率分布直方图Fig.3 Histogram of probability distribution of roundness error
由图3可知:圆度误差f=41.924 5 μm, 圆度测量不确定度uf=2.194 5 μm。
③结果比较。
GUM法的评定结果为:圆度误差f=41.926 2 μm;圆度测量不确定度uf=2.274 1 μm。
蒙特卡罗法的评定结果为:圆度误差f=41.924 5 μm;圆度测量不确定度uf=2 194 5 μm。
由以上评定结果比较可知,GUM法和蒙特卡罗法评定圆度测量不确定度的结果基本一致,并且完全满足精度要求。因此,蒙特卡罗法以其评定结果准确、可靠,评定过程简单、高效的优点,为测量不确定度评定提供了一种新的方法。
4 结束语
本文分别采用了GUM法、蒙特卡罗法对直角坐标系下的圆度误差进行了测量不确定度评定。试验数据表明,两种方法的评定结果基本一致。GUM法是按照《测量不确定度评定指南》中的评定步骤进行评定的,需要求出圆度误差数学模型中各个参数的传递系数。误差模型复杂或非线性时,参数之间的相关系数难以求出,对圆度测量不确定度的评定带来了困难。而蒙特卡罗法则采用数据模拟的方法进行圆度测量不确定度的评定,针对误差模型复杂或非线性的情况,其评定更为便捷。因此,蒙特卡罗法评定圆度测量不确定度是一种行之有效的方法。该方法也可应用到其他形位误差测量不确定度的评定,在测量领域具有一定的工程实用价值和应用前景。
参考文献:
[1] 中国计量研究院.测量不确定度的评定与表示:JJF1059.1-2012[S].国家质量监督检验检疫总局,2012.
[2] 周桃庚.用蒙特卡洛法评定测量不确定度[M].北京:中国质检出版社,2013.
[3] 齐秀彪.圆度误差数学模型的建立与仿真分析[J].本溪冶金高等专科学校学报,2001,3(2):26-28.
[4] 赵凤霞,张琳娜,方东阳.圆柱度误差评定及其不确定度估计[J].机械设计与研究,2009,25(4):89-91.
[5] 倪骁骅.形状误差评定和测量不确定度估计[M].北京:化学工业出版社,2008.
[6] 连慧芳,陈晓怀.基于蒙特卡罗方法的圆度测量不确定度评定[J].工具技术,2010,44(6):82-84.
[7] 吴呼玲.基于蒙特卡罗法与GUM法的直线度测量不确定度评定[J].工具技术,2017,51(5):104-107.
[8] 吴呼玲.基于蒙特卡罗法的平面度测量不确定度评定 [J].计算机测量与控制,2017,25(5):262-265.
[9] 郭连湘,何频.计量仪器与检测[M].北京:化学工业出版社,2006.
[10]王东霞,宋爱国.基于三坐标测量机的圆度误差不确定度评估[J].东南大学学报,2014,44(5):952-956.
[11]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2010.
[12]高正明,贺升平,赵娟.一种新的不规则实体密度测量方法研究[J].自动化仪表,2012,33(12):10-12.

