化归思想在高中数学解题过程中的应用探讨

李舒怡

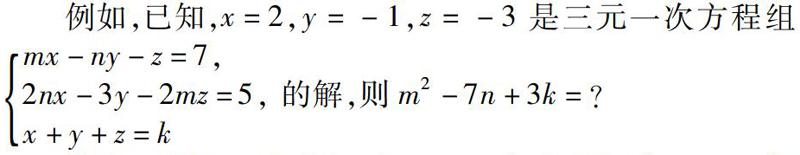
【摘要】高中数学相较于初中来说难度整体上有了提升，知识体系化也更强，在学习过程中我们不禁发出“数学难，难于上青天”这样的感慨.面对数学这一难题，我们在不断探索适合自身的学习方法与途径，划归思想，在高中数学传统解题思想的基础上，更加注重对我们数学思维的培养，凭借其在解题中较高的准确率，得到了广泛应用.本文以化归思想在高中数学解题过程中的应用为研究内容，通过案例分析，介绍这一解题思想的优势.

【关键词】化归思想；高中；数学；解题

区别于初中阶段的数学学习，高中数学学习内容的重点是对于解题思路的整理，以及在原有解题思路上的拓展.在此过程中，以降低问题难度、提高解题正确率为主要特点的化归思想得到了普及，在此过程中，我们高中生的数学思维能力也得到了明显提升.

一、化归思想概述

在问题的分析、解决过程中，需要利用已知的信息对未知内容进行转化，使其更加简单，这就是化归思想.从辩证的角度来看，化归思想运用动态研究理念，关注不同信息之间存在的必然联系，从而为研究工作提供更加简单的路径.在高中数学解题过程中，化归思想有着较为普遍的应用.

二、化归思想在高中数学解题中的形式

在高中数学解题过程中，化归思想的应用较为广泛，利用知识点之间的相关性，进行问题转化，能够有效提高解题速度，降低解题难度.在高中数学解题中，常见的化归思想包括高维空间向低维空间的转化、多元向一元的转化等，尽管，化归思想在一定程度上增加了解题步骤，但是，却大大提高了解题的准确率.

（一）多维空间向低维空间的转化

在高中数学的学习过程中，经常遇到解高维几何题目，由于空间几何问题一直以来是高中数学考试的重點，因此，掌握多维空间向低维空间转化的思想，能够有效提高此类数学题的解题效率.高维空间是由多个一维空间所叠加起来的，通过多维空间中的立体图形进行垂直坐标系的二维投影，得到平面几何图形，并进一步分析不同坐标系中平面几何图形的关系，以得到最终的答案.

（二）多元向一元的转化

在高中数学传统解题思路中，面对多元函数类型的题目，很多时候我们所想到的是如何消除未知数，然而，在实际解题中，一元未知数的消除较为简单，多元未知数消除的难度则相对较高.利用化归思想，可以将多元未知数向一元未知数进行转换，从而降低解题难度，提高解题效率.

例如，已知，x=2，y=-1，z=-3是三元一次方程组mx-ny-z=7，2nx-3y-2mz=5，x+y+z=k 的解，则m2-7n+3k=？

解析 这里可以看出，在三元一次方程组中，x，y，z都是已知量，这里需要对m，n进行求解，并将最终结果代入方程中进行计算.通过不断的消元，能够将三元一次方程组转变为二元一次方程组，继续消元，从而得到一元一次方程，解题也就变得简单了.

三、经典数学中的化归思想

化归思想在高中数学解题中的应用，不仅能够降低题目难度，还可以帮助我们进行探究式学习，找到解题的新方法.在经典数学中，化归思想也有着较为普遍的应用，其中，“数学归纳法”就是使用了化归思想，作为高中阶段最为重要的解题方法之一，“数学归纳法”巧妙利用了对现象的分析、总结，提出可验证的结论，将原本看似难以解决的问题变得简单化.

例如，在一个不透明的袋子里，放了5个带有颜色的小球，要求我们设计一个证明方法，以证明袋子里的小球全部是黑色的.该题所考查的是我们对于知识点之间关系的应用，在实际案例中体现化归思想，对于证明方案的设计，同时也考查了我们的数学思维能力.在该题的设计过程中，所使用的证明方法并不唯一，可以使用“完全归纳法”，也可以使用“不完全归纳法”，我们对于化归思想的应用能力也将得到提升.

四、高中生化归思想的培养

对于我们高中生来说，面临着巨大的升学压力，数学作为传统专业课程，在高考中占有主要地位，然而，在高中数学的学习过程中，除了对相关知识点进行掌握以外，我们还要在数学思维能力方面进行加强.化归思想的培养，所需要的不仅仅是大量的练习，更是对以往所学知识点的系统化应用，这对于我们大部分人来说都存在一定的难度，化归思想的培养，需要注意以下几个方面的内容.

（一）加强基础知识的体系化建设

对于以往所学过的数学知识，需要进行系统化的整理，在此过程中，我们要善于发现不同知识点之间存在的关系，并以此为线索，完成原本孤立的知识点的体系化建设，为化归思想的应用奠定基础.

（二）合理利用教材中的题目

在高中数学教材中，化归思想得到了很好的体现，其中数学题目的解答方法并不唯一，在传统解答方法的基础上，也可以借助化归思想完成.不仅如此，在化归思想的学习过程中，合理利用教材，能够保证学习方向的正确性，避免相关知识点超出高中数学知识体系，打击我们对化归思想学习的积极性.

（三）理论与实践相结合

数学学习的最终目的是解决生活中所遇到的数学问题，化归思想的学习也是如此，通过在生活实践中使用化归思想，有助于我们对这一解题思想的深入理解，以及数学思维能力和应用能力的提高.

五、总 结

化归思想在高中数学解题中的应用，不仅丰富了我们在数学解题过程中的思路，还帮助我们实现了数学基础知识的体系化建设.除此之外，对于化归思想的应用，还可以覆盖到其他专业课程的学习之中，有助于我们学习能力的全面提高.

【参考文献】

[1]靳世杰.高中数学化归思想教学之我见[J].数学学习与研究，2014（17）：56.

[2]于洋，傅海伦，王剑.新课程下化归思想在解题中研究的反思[J].中学数学杂志，2015（8）：4-6.

[3]朱涛.论转化与化归思想在高三解题中的运用[J].陕西教育（教学版），2015（9）：35.