基于用户特征和时间权重的协同过滤算法
孙克雷,王琰
(安徽理工大学 计算机科学与工程学院,淮南 232001)
0 引言
随着互联网的普及和迅速发展,每天都能接收到大量的信息,互联网在满足用户对信息需求的同时,也使得用户难以在海量信息中获得真正对自己有价值的那部分信息,从而降低了信息的利用率,出现了“信息过载”的问题。推荐系统则是为解决这一问题产生的,它是一种帮助用户在众多的选择中做出决策的智能系统,当用户浏览自己喜欢的物品时,推荐系统会根据他的喜好相应地推荐出与当前物品相关的其他物品,从而提高了查找信息的效率。目前已经出现了各种形式的推荐系统[1-2]。
在推荐系统中有许多经典的推荐算法,协同过滤算法就是其中之一,但在生活实践和实验研究中发现它还有一些潜在的问题,例如数据稀疏[3-4]、用户兴趣难以获取[5]和冷启动[6]等问题。基于这些急需解决的问题,国内外学者和专家对此都做出了巨大的努力,他们从各个方面剖析问题,并取得了一些成果。
刘东辉[7]等人通过定义时间指数函数来反映用户兴趣随时间增长而发生变化,并通过建立用户的特征矩阵,采用一种新的相似度度量方法计算出目标用户的最近邻居集合。赵文涛[8]等人主要是对用户相似度进行改进,提出对Logistic时间权重函数与用户特征属性进行加权计算,形成一种新的相似性度量模型,在新的模型下更好的求出目标用户的相似集合。陈志敏[9]等人在计算用户相似性过程中引入与时间相关的兴趣度,使得得到的最近邻居更加准确,预测评分时,通过衡量用户信任度来体现各邻居对目标用户最终推荐的贡献程度。
上述研究将时间指数函数加入到相似度的度量中,体现了用户兴趣随时间变化规律;但未考虑不同用户兴趣变化速率的差异,针对这个问题,本文提出了一种基于用户特征和时间权重的协同过滤算法。首先在修正的余弦公式中引入用户特征参数,得出一个新的相似度矩阵;然后由新的相似度矩阵求出邻居用户,得到较为精确的最近邻居集;最后求预测评分时,引入了时间函数,但在时间函数中考虑到不同时间范围用户的兴趣衰减不同,提出了全新的时间函数,以解决用户兴趣变化问题,从而求出新的预测评分,为用户做出推荐。
1 相关工作
在传统的协同过滤算法中,一般假定用户集合用 U={U1,U2,…,Um}表示,项目集合用 I={I1,I2,…,In}表示,两者组成一个用户-项目评分矩阵,且该矩阵是一个m×n阶矩阵,并用R(m×n)表示,如表1所示。
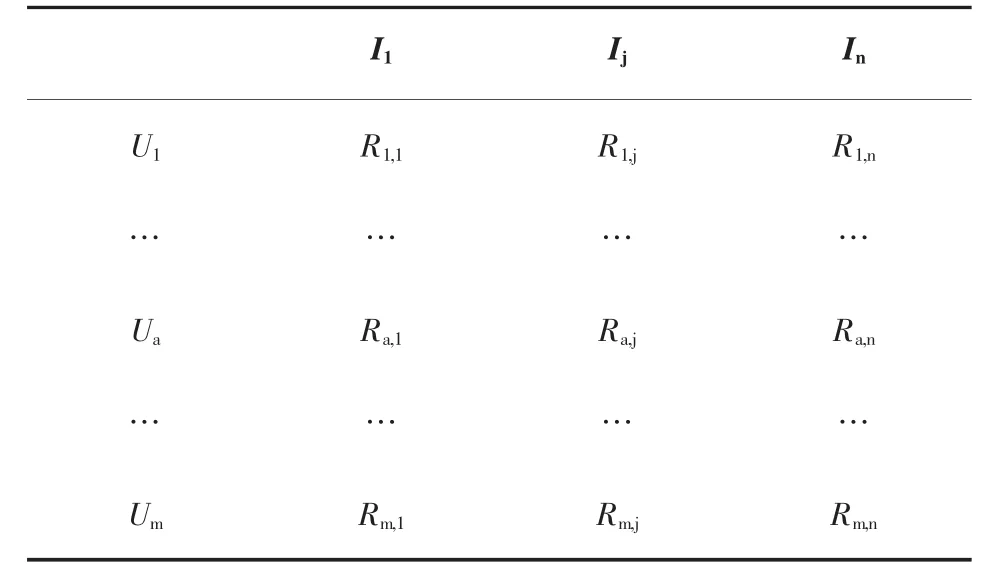
表1 用户-项目评分矩阵R(m×n)
其中,矩阵的行数为m行,列数为n列。m行表示有m个用户,n列表示有n个项目。假设某一用户 Ua对项目 Ij(其中 Ua∈U,Ij∈I)的评分为 Ra,j,这个评分反映了用户Ua对项目Ij产生兴趣的程度。
基于用户的协同过滤算法首先利用传统的相似度公式求出目标用户的最近邻居集[10],再根据邻居用户的评分矩阵来得出目标用户的预测评分。这里采用修正的余弦来度量用户u和v的相似度,其表达式为:
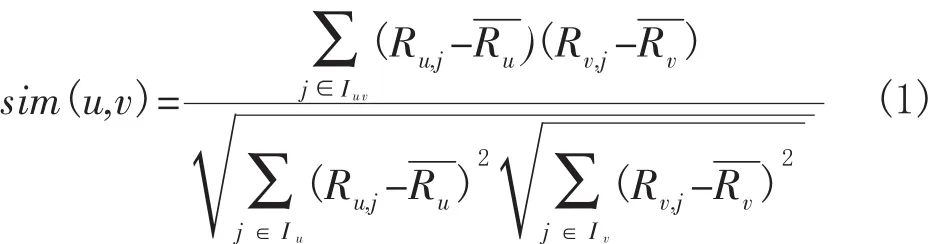
其中,u,v分别代表用户u和用户v;Iuv表示用户u和用户v共同评分的项目集合,Iu和Iv分别表示用户u,v评分的项目集合;Ru,j和Ru代表用户u对项目j的评分和平均评分,Rv,j和Rv代表用户v对项目j的评分和平均评分。计算结果sim(u,v)的值落在[-1,1]区间中,如果sim(u,v)的绝对值越大,则表明用户u、v间的相关程度就越大。
根据公式(1)求出两两用户的相似度值所构建的相似度矩阵,从大到小排序选出s个近邻用户作为最近邻居集S,使用公式(2)可以计算目标用户u对推荐项目的预测评分,如式2所示:
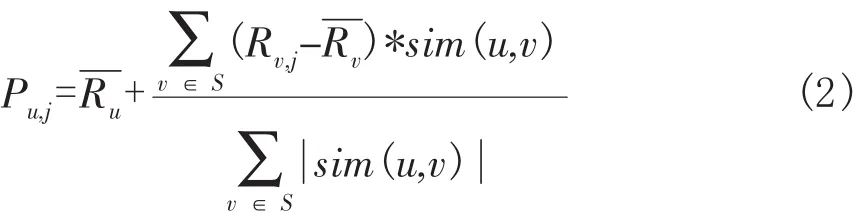
其中Pu,j表示目标用户u对项目j的预测评分,sim(u,v)表示用户u和用户v的相关系数。
2 基于用户特征和时间权重的协同过滤
该算法利用Movie Lens数据集,首先根据数据集中的用户信息表提取用户特征信息,并对特征进行分类标记,经过量化处理后得到实验所需数据。再把其引入到修正的余弦相似性计算中,计算出基于用户特征的用户相似性,从而得到较为精确的最近邻居集。然后在求预测评分时加入时间函数,通过给评分赋予权重来反应用户的兴趣变化,从而降低用户兴趣的迁移对推荐结果的影响,最终获得符合用户喜好和需求的推荐。
2.1 用户特征
2.1.1 用户特征的提取
用户特征属性相对客观稳定,在实际生活中,特征类似的两个用户,其兴趣往往有较大的相似性,而具有不同特征的用户,其兴趣偏好则存在很大的差异性[11]。一般在注册一些网站时,用户需要对自己的基本信息进行备注,如年龄、性别、职业等。本文将用户填写的特征信息进行数字化处理后形成数据集加入到相似度计算中,减小了由传统方法得到的相似用户对目标用户的影响,从而找出较为精确的最近邻居集合。根据所用的数据集,这里简化地画出一个用户特征属性表,如表2所示:
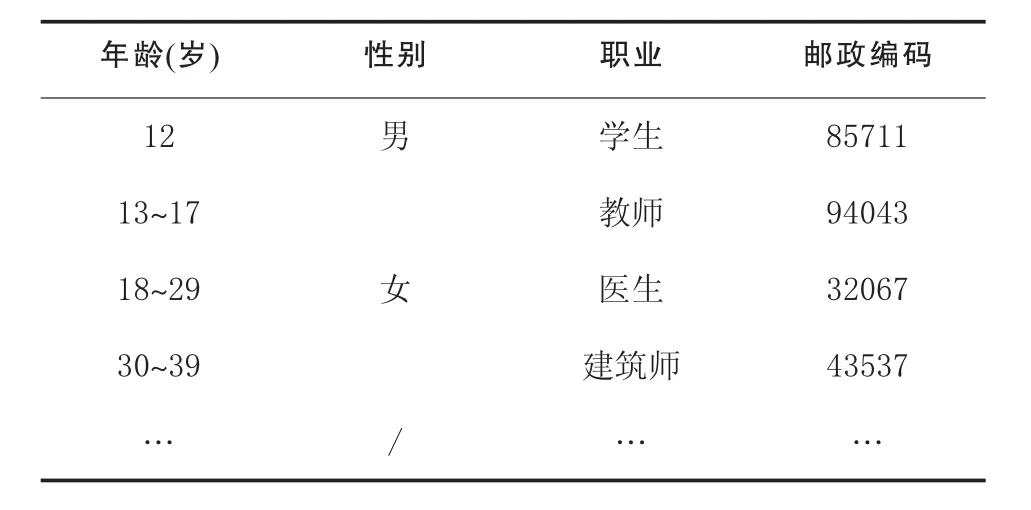
表2 用户特征属性表
2.1.2 基于用户特征的相似度计算
1)根据上节中建立的用户特征属性表,把用户特征主要分为四类即年龄、性别、职业、邮政编码。其中根据年龄段的分类对其编号可表示为{0,1,2,3,…};把用户的性别分别记为{“M”,“F”},M表示0,F表示1;对职业的分类,这里把每一种出现的职业都进行编号,结果可为{0,1,2,3,…}。
2)根据第一步得到的特征数据集,可以计算用户之间的特征相关性。特征相关性表示两用户之间相同特征的个数在特征总数中所占的比重,并用sim1表示。其中两用户之间的特征属性比较我们用Compare函数表示。计算过程如下:
假设有一个关于m、n的用户特征矩阵A=[m,n],其中m表示用户个数,n表示特征个数。Au,j表示用户u的第j个特征,Av,j为用户v的第j个特征,当Au,j=Av,j时,Compare值为1,当Au,j≠Av,j时,Compare值为0。Compare值为1时表示用户u,v的特征相同,Compare值为0时表示用户u,v特征不同,特征相似性计算如下所示:
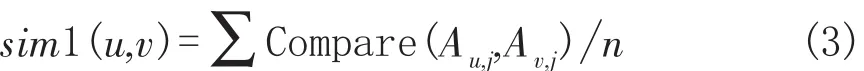
3)结合以上两个步骤将求出的公式(3)加入到修正的余弦相似性系数中,进一步计算得出改进的基于用户特征的相似度sim(u,v),公式如下:
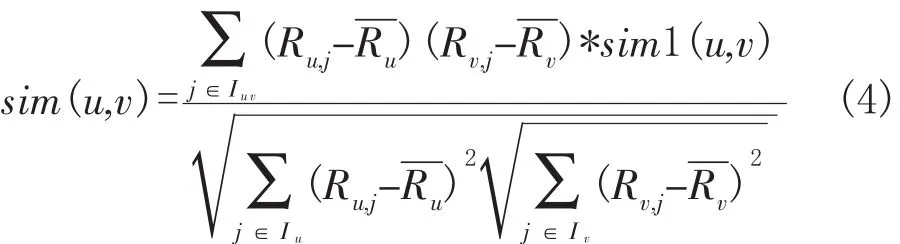
2.2 时间函数
用户的兴趣爱好是随着时间发生变化的,但传统算法并未考虑到用户在不同时间的兴趣变化,针对推荐系统中兴趣迁移的问题,本文引入时间函数的方法赋予评分时间权重来体现用户的兴趣偏好差异,用户对项目评分的时间越远,其权重越小,评分的时间越近,其权重就越大,使用户兴趣的迁移对推荐算法产生的影响有所缓解,以实现更加准确的实时推荐。
通过实验研究发现用户兴趣的变化符合某种非线性递减的规律,本文通过时间衰减函数f(u,t)来表示这种规律,公式如下:

其中,f(u,t)为时间衰减函数,t表示当前时刻,tu,j表示用户u对项目j评分的时间,I表示用户u对项目j的评分集合,k表示时间范围,每当取不同的k值时,反映每个不同范围内用户对项目的兴趣衰减变化情况,从而得出用户兴趣发生迁移的转折点。
2.3 基于用户特征和时间权重的协同过滤算法
针对传统的协同过滤算法未能反映出用户自身特征和用户兴趣随时间变化的问题对推荐结果产生的影响,本文提出了基于用户特征和时间权重的推荐算法。首先根据2.1节中的用户特征参数(公式3)求出新的相似性关系(公式4),再结合2.2小节中提出的时间函数(公式5)给项目评分赋予时间权重,共同引入最终的预测评分公式,从而能够在考虑到用户本身属性的同时又能够反应出用户的兴趣变化,最后得出目标用户u对任意项目j(j∈I)新的预测评分,其表达式为:

其中S'表示加入用户特征之后新的最近邻居集,从公式(6)中可以看出,用户u对未评分项j的最终预测评分Qu,j是在传统的预测评分Pu,j基础上,通过用户u的最近邻居加权得到。其中权重由两部分组成,一是在求最近邻居与目标用户的相似度中融入了用户特征,相似度越高,权重就越大;二是根据相似用户对目标用户未评分项的评分时间进行时间加权,评分时间离当前时间越短,权重越大,反之权重越小。
2.4 算法描述
输入:用户-评分矩阵,用户-特征矩阵,用户-项目-评分时间矩阵。
输出:推荐项目列表。
Step1.计算传统的预测评分。首先利用公式(1)得到目标用户的邻居用户,再利用所得邻居用户通过公式(2)计算出目标用户未评分过的项目的传统预测评分。
Step2.获取用户特征参数。加入的用户特征参数是为了减小由传统方法得到的相似用户对目标用户的影响。首先利用公式(3)求出两个用户之间的特征相关性,然后将其加入到修正的余弦相似度公式(4)中,最后得到一种新的用户特征相似度。
Setp3.构造体现用户兴趣迁移的时间函数。用户兴趣容易受外界环境因素的影响,兴趣经常会发生改变,针对传统推荐算法没有考虑到用户兴趣会随着时间的推移而发生迁移的问题,本文通过公式(5)的时间函数,解决了用户兴趣偏好发生变化的问题,使时间最近产生的兴趣权重最大,从而提高了推荐的效果。
Step4.生成推荐列表。根据公式(6)在最终预测评分中引入时间函数,得出新的预测评分,形成Top-N推荐列表。
3 实验结果与分析
针对以下三个问题进行实验研究:(1)选取用户发生兴趣迁移的K值;(2)不同推荐数目对推荐性能的影响;(3)在推荐性能上本文算法与其他算法相对比的结果。
3.1 实验数据集
本文使用Movie Lens网站提供的数据作为实验数据集[12]。Movie Lens数据集有3个不同大小的版本,本文选用其中的ml-100k数据集。该数据集记录了943个用户对1682部电影的十万条评分信息。每个用户可以给电影评5个不同等级的分数(1-5分),用户对电影评分的高低代表了用户对电影的喜爱程度,而且每个用户对电影进行评分的数量都超过了20部。本文利用数据集中三个用户文件即u.base、u.test和u.user进行实验研究。其中u.base主要存放了80%的实验数据,用作训练集;u.test中存放了20%的实验数据,用作测试集,训练集和测试集主要由用户ID、项目ID、评分以及时间戳构成;u.user主要存放着用户特征信息包括性别、年龄、职位、邮编。
3.2 实验评价标准
为实现实验结果本文使用Matlab软件平台进行相关实验,在实验结果中对算法的推荐性能进行评价,评价的标准是平均绝对误差(Mean Absolute Error,MAE)[13,17],因为MAE主要用于度量预测评分与实际评分之间的偏差,如果偏差越小,则预测的准确度就越高。MAE的定义为:

上式中设定用户的预测评分集合pi表示为{p1,p2,...,pn},真实评分集合qi表示为{q1,q2,...,qn}。
3.3 实验分析
在传统UserCF算法基础上,采用加入非线性时间函数,解决了在一段时间内用户发生兴趣偏移的问题。其中,在时间函数中引入了参数K作为一种时间段,在参数K选取中,不同的参数K间接对实验的MAE有着不同的影响。K值可分别取值为604800(一周)、2592000(30天)、10368000(一季度)、15768000(半年)和31536000(一年)。得到的实验结果如图1所示。
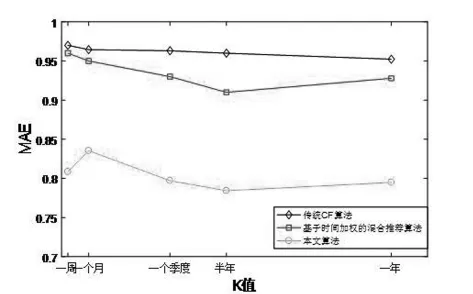
图1 选取最佳时间间隔K值
由图1可得知传统CF算法是呈现逐渐下降趋势的,但是推荐的效果不是很好,MAE的值都高于0.9,但是文献[14]即基于时间加权的混合推荐算法相对于传统的推荐算法来说效果会好一点,可以看到随着K值的增大MAE的值会有先下降在上升的现象。本文算法也有类似现象,但是本文算法在K值为一个月时,MAE值先发生上升后发生下降的现象,这说明用户一开始对项目还处在接受期,还没有产生兴趣,后来随着时间的推移开始产生兴趣,此时MAE一直处于下降趋势,但是到了半年之后即K为15768000时,MAE值又有小幅上升趋势,可能的原因是用户对该项目的兴趣正在发生改变,现在网络发展很快,各种商品琳琅满目,更新换代特别快,用户对某一项目感兴趣的时间发生变化也就越来越快。因此,由图1可得,当K值为半年时,用户对项目的兴趣度会发生转变。
针对本文所提出的算法,根据不同的推荐数目(top-10、top-20、top-30、top-40)在相同K值的情况下观察MAE的大小,实验的结果如图2表示。
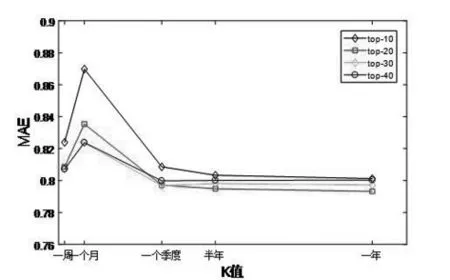
图2 不同推荐数目的MAE值比较实验
图2 的实验结果显示当K值相同时不同推荐数目对应的MAE值不同,随着K值的增大,推荐项目为10的MAE值总是比其他三个推荐项目数的MAE值高。推荐项目过少可能会导致预测评分与真实评分偏差过大,从而导致MAE值过高。当K值为一个月时,不同推荐数目的MAE值都出现快速上升现象,随后又都开始下降,发生显著上升和下降的原因可能是用户首先对项目进行了解,但并没有产生兴趣,后来随着事件推移发生兴趣,MAE缓慢下降。当在一个季度期间时,可以看出推荐项目为30是较好的。当K值在一个季度之后,MAE值趋于平缓,此时推荐项目为20的时候,效果较好。
这里将本文算法与传统UserCF算法、文献[15]和文献[16]在推荐性能上进行比较,其中文献[15]是面向电影推荐的时间加权协同过滤算法的研究,文献[16]是基于时间加权的协同过滤算法。实验结果比较如图3所示。
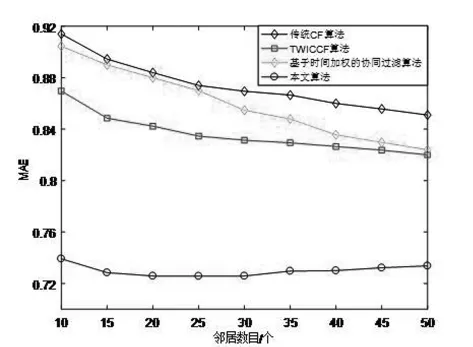
图3 不同推荐算法的MAE值比较
通过实验图3可知,本文算法在准确性方面优于传统的UserCF算法和图3中其他两个算法,因为本文的MAE值总体都比其他算法的MAE值低,即平均绝对误差较小,所以准确率略高。不过随着邻居数目的增多,MAE值发生略微上升现象,这是因为邻居用户的不断增多导致预测评分公式计算出的预测评分与实际评分之间的误差变大,从而使得实验的MAE值会有略微提高,准确率也会发生略微下降。
4 结束语
针对当前UserCF算法未能反映出用户自身特征和用户兴趣随时间变化对推荐性能产生影响的问题,本文提出了基于用户特征和时间权重的推荐算法。该算法中的用户特征属性主要包括性别、年龄、职业等,首先根据用户特征信息求出用户的特征相关性,为目标用户产生更加准确的相似用户。然后再加入时间函数求出预测评分,最后给用户做出推荐。实验结果验证了该算法在推荐的结果上具有较高的准确性。但本文算法仍有一些需要改进的地方,其中算法效率还不够理想,因为随着邻居数目的增加,推荐的性能没有发生明显地提高;另外在时间函数方面还存在不足之处,因为利用时间函数求出的预测评分的准确性还有待提高,因此如何有效的提升运算效率,并进一步改进推荐的准确率,这是下一步要研究的工作。
[1]SARWAR B,KARYPIS G,KONSTAN J,et al.Analysis of recommendation algorithms for ecommerce[C]//ACM Conference on Electronic Commerce.New York:ACM,2000:158-167.
[2]SCHAFER J B,KONSTAN J A,RIED J.E-commerce recommendation applications[J].Data Mining and Knowledge Discovery,2001,5(1/2):115-153.
[3]付芬,豆育升,韩鹏,等.基于隐式评分和相似度传递的学习资源推荐[J].计算机应用研究,2017,(12):1-8.
[4]WEI S,YE N,ZHANG S,et al.Collaborative filtering recommendation algorithm based on item clustering and global similarity[C]//2012 Fifth International Conference on Business Intelligence and Financial Engineering(BIFE).IEEE,2012:69-72.
[5]Qi Liu,Enhong Chen,Hui Xiong,et al.Enhancing collaborative filtering by user interest expansion via personalizedranking.[J].IEEETransactionson SystemsMan&Cybernetics,2011,42(1):218-233.
[6]于洪,李俊华.一种解决新项目冷启动问题的推荐算法[J].软件学报,2015,26(06):1395-1408.
[7]刘东辉,彭德巍,张晖.一种基于时间加权和用户特征的协同过滤算法 [J].武汉理工大学学报.2012,34(5):144-148.
[8]赵文涛,成亚飞,王春春.基于Logistic时间函数和用户特征的协同过滤算法[J].计算机应用与软件,2017,34(2):285-289.
[9]陈志敏,李志强.基于用户特征和项目属性的协同过滤推荐算法[J].计算机应用,2011,31(7):1748-1750.
[10]王茜,王均波.一种改进的协同过滤推荐算法[J].计算机科学,2010,37(6):226-228.
[11]李永超,罗军.基于用户部分特征的协同过滤算法[J].计算机系统应用,2017(26)03:204-208.
[12]MovieLens数据集[EB/OL]https://grouplens.org/datasets/movie-lens/.
[13]HERLOCKER L J,KONSTAN A J,TERVEEN G L,et al.Evaluating collaborative filtering recommender systems[J].ACM Transactions on Information Systems,2004,22(1):5-53.
[14]郑鹭升.基于时间加权的混合推荐算法研究[D].厦门:厦门大学,2013.
[15]兰艳,曹芳芳.面向电影推荐的时间加权协同过滤算法的研究[J].计算机科学,2017,44(04):295-301+322.
[16]丛晓琪,杨怀珍,刘枚莲.基于时间加权的协同过滤算法研究 [J].计算机应用与软件,2009,26(08):120-121+140.
[17]纪科.融合上下文信息的混合协同过滤推荐算法研究[D].北京:北京交通大学,2016.

