600MW超临界机组协调控制系统模型优化研究

曹喜果　张永涛　单英雷

摘要：超临界机组多变量耦合、强非线性、不确定性等特点给控制系统设计及调试带来一定的困难，而研究超临界机组主要被调量的动态特性并建立结构简单的协调模型可很好地解决以上问题。该文将机理建模与试验建模进行结合，对结构复杂的协调控制模型进行优化，针对某600MW超临界机组，在机理分析模型结构的基础上，根据模型之间的共性，对模型结构进行简化。通过现场试验获取主要调节量即燃料量、给水量、阀门开度扰动下的动态特性，采用改进的粒子群算法辨识获得600mW超临界机组三输入三输出的数学模型，该模型动态特性与理论分析保持一致，验证模型可靠性。此外，模型结构简单且能很好地反映超临界机组的动态特性，可为进一步研究超临界机组及控制器的设计提供参考。

关键词：超临界机组；动态特性；机理分析；模型辨识

文献标志码：A

文章编号：1674-5124（2018）02-0147-06

0引言

近年来，超（超）临界机组以高效率、低排放的优势在国内得到了越来越广泛的应用。超（超）临界机组与亚临界相比，对象特性及工艺流程发生了较大的变化，表现出多变量、强非线性、强耦合性、蓄热能力小等特点，从而给控制系统设计及调试带来一定的困难。而掌握超（超）临界机组的动态特性并建立其数学模型可很好地解决以上问题。

对于超（超）临界机组来说，目前主要采用机理建模的方法。由于其模型与亚临界的区别主要在于蒸发系统，为此，不少学者对蒸发系统模型进行了分析研究。此外，对超（超）临界机组整体模型的研究也逐渐增多。以上的机理建模较好地反映了机组参数之间的内在联系，但建模过程繁琐，模型形式复杂，不利于控制算法的设计与仿真。智能算法使得采用试验法辨识获得超（超）临界机组的数学模型变得相对容易，但是试验法获取机组的动态特性较为麻烦，既要保证机组的安全运行，又要体现出主要参数的变化趋势。

超临界机组协调控制模型对其动态特性分析及后续设计非常重要，目前可参考的模型结构复杂，不利于后续分析设计。本文对协调控制模型进行优化研究，在某600mW超临界机组上进行给水量、给煤量、阀门扰动试验，在机理分析模型结构的基础上，采用改进的PSO辨识获取协调控制系统三输入、三输出模型。所得模型结构简单，能反映超临界机组的动态特性，可为协调控制系统控制器的设计及今后现场调试提供参考。

1机理分析模型结构

1.1借鉴汽包炉思路

对于汽包炉来说，demello模型是其经典模型，在此研究之前，该汽包炉经典模型很少用到直流炉建模上，主要原因在于该模型下直流炉蓄热系数的求取存在一定的困难，而求取了该蓄热系数，使得以上的建模思路成为可能，为直流炉简化模型的建立提供了方便。对于双输入、双输出的汽包炉，经典模型（demello模型）结构如图1所示。

对于直吹式制粉系统来说，煤在磨煤机中磨成煤粉送人锅炉燃烧，转化为热量的过程主要表现为惯性及延迟环节。即：

则其拟合效果如图3所示，利用模型转换公式可实现模型结构的灵活转化。在具体的操作过程中，可利用该公式确定初始范围，后根据拟合效果再做微调。鉴于此，将机理辨识模型转化为多阶惯性环节的乘积形式，既能很好地反映超临界机组协调控制的动态特性，又结构简单，为后期设计合理的控制方案提供模型参考。

2超临界机组动态特性试验

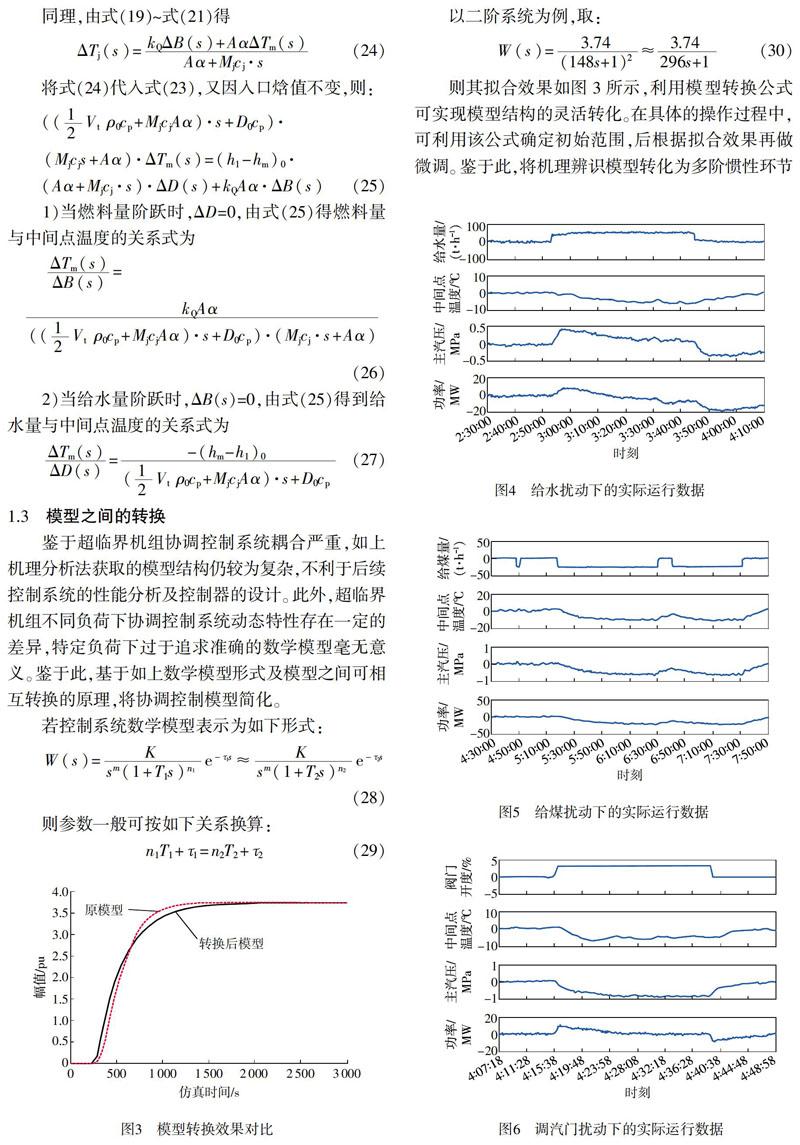
对某600mW超临界机组在524mW（87%负荷点）稳定工况下做煤、水、阀门阶跃扰动試验。试验过程中，机组控制切为手动方式。图4为给水量W阶跃50t/h时，机组功率Ⅳ、中间点温度（分离器温度）T、主汽压pT的变化趋势，采样时间12s。图5为给煤量曰阶跃10t/h，N、T、pT的变化趋势，采样时间24s。图6为调汽门肛阶跃3.175%，N、T、pT的变化趋势采样时间5s。

给水扰动下的响应曲线如图4，给水量阶跃扰动时，中间点温度下降；主蒸汽压力先上升后下降并恢复到初始值：机组功率是先上升后下降，功率最终稳定在低于初始值的位置。

图5为燃料量阶跃时响应曲线，当燃料量阶跃减少时，煤水比减小，所以中间点温度下降，蒸发量减少，进而蒸汽压力、机组的功率都降减小。

图6中，当阀门阶跃增加，中间点温度略有下降，并稳定在较低的温度；主汽压下降并稳定在较初始值低的状态：功率先增大后恢复到初始值。

3模型辨识与仿真

3.1模型辨识

基于以上机理分析模型结构形式及模型等效转换原理，运用改进的粒子群算法对模型进行辨识，选取各模型结构形式为

以给水量-主蒸汽压力辨识为例，采样数据与所得模型的拟合效果如图7所示。由图中拟合效果可得：采用改进的PSO算法辨识获得的超临界机组动态模型拟合误差较小，该模型结构简单，较好地反映了超临界机组的动态特性。

3.2模型仿真

针对如上辨识所得的超临界机组协调模型，对其动态特性进行仿真研究，为协调系统优化提供理论分析和计算依据。1000s时，给煤量B阶跃增加10t/h，煤水比增大，蒸发量增大，主蒸汽压力pT增大，并达到新的稳定状态；给水量W增加50t/h时，pT先上升后下降并恢复到初始值；调门开度μ增加，pT下降并稳定在较初始值稍低的状态。主蒸汽压力pT响应曲线如图8所示。

1000s时，给煤量W阶跃增加10t/h，中间点温度Tm增大；给水量W增加50t/h时，Tm下降；中间点温度Tm响应曲线如图9所示。

同理，1000s时，给煤量B阶跃增加10t/h，机组功率增大：给水量W增加50t/h时，机组功率N是先上升后下降，最终稳定在低于初始值的位置：调门开度μ增加3%时，N先增大后恢复到初始值。机组功率Ⅳ的响应曲线如图10所示。以上模型动态特性与理论分析一致。

4结束语

通过机理分析法确定模型结构形式，利用模型之间的共性进行简化，再利用改进的PSO算法，辨识获取了超临界直流炉三输入、三输出协调控制模型，该模型结构简单、很好地反映了超临界机组的动态特性，可为超临界机组深入分析及控制器设计提供方便，具有较强的实用价值。