高准确度铯—氦光泵磁强计的粒子数密度配比研究

伏吉庆　张伟

摘要：为研发高准确度铯-氦光泵磁强计探头的制备工艺，该文通过分析铯、氦两种混合物质的气室内各组分间的潘宁电离和自旋交换碰撞过程，从理论上给出铯-氦磁强计的最佳粒子数配比关系NCs：NHe≈1.9：1。为验证该理论，搭建一套铯-氦磁强计系统，分别通过调节温度和激励微波来控制铯原子和氦原子的数密度，当磁共振信号达到最优化状态时，测量铯氦粒子数比值为NCs：NHe≈1.6：1。考虑到理论计算时对亚稳态氦原子退极化率的保守估算和实验过程中对气室内部温度的测量误差，该理论值和实验结果吻合度较为一致。研究结果表明：在制作铯-氦光泵磁强计探头气室时，铯原子与亚稳态氦原子的原子数密度比值应该介于1.6～1.9之间。

关键词：铯-氦磁强计；自旋交换碰撞；化学电离；激光泵浦

文献标志码：A

文章编号：1674-5124（2018）02-0001-05

0引言

在计量学中，任何一个磁场测量值皆需溯源回基准磁场装置。为保证基准磁场量值的准确度，除了需要产生足够稳定的标准磁场，还需将产生的标准磁场测量得足够准确。因此高准确度的基准磁强计是磁计量学的一个核心技术。我国的磁基准装置历经几次改良，目前使用的是欧弗豪泽质子磁强计，其复现磁场的准确度受限于本身的噪声，可以达到0.1nT。但是由于质子磁强计需要外加激励磁场，难以工作在低于20μT的弱场环境中，同时其准确度也难以满足几年来突飞猛进的高灵敏度磁强计的量值溯源需求，因此改进基准磁强计技术的需求迫切。

光泵磁强计不需要外加激励磁场，可以工作在更微弱的磁场（1～20μT）中，同时信噪比远高于质子磁强计，但是由于泵浦光场的ACstark效应往往会带来1-10nT的转向误差，导致光泵磁强计准确度不高。为了消除光频移误差，Blinov等在1979年成功研制了一种利用碱金属铯和氦气混合气室作为工作物质的铯-氦光泵磁强计。这种磁强计采用了间接光泵浦技术，可以有效消除转向误差，使光泵磁强计的准确度大幅提升，成为目前地磁范围内使用准确度最高的磁强计之一，在计量学上意义重大。

俄罗斯计量院在2000年利用铯-氦光泵磁强计搭建了新一代国家恒定弱磁基准装置，将准确度提升到0.003～0.03nT的量级，该装置是目前公开报道的准确度水平最高的基准磁场装置。研究拥有自主知识产权的铯氦光泵磁强计，提升我国磁场基准水平无疑拥有重要的战略意义。

本文就铯-氦磁强计的核心部件，铯-氦混合气室的制备工艺开展研究。铯-氦混合气室制备过程中中将铯原子与亚稳态氦原子的粒子数密度精确控制在合适的比例是一个关键操作，只有在最佳比例时磁强计信号才能达到最佳信噪比。

Blinov等给出了铯-氦气室中氦气的最佳充气压强的经验值以及激励亚稳态⁴He的优化参数，但是不同时期的文献中给出了不同的优化结果，并缺少理论分析。为了解决该问题，本文在理论上通过对铯-氦混合气体各种粒子之间相互作用过程的分析，得到铯-氦粒子数密度的最佳估值，并通过实验来验证该理论的准确性。

1理论

铯-氦光泵磁强计是通过氦原子的极化自旋磁矩来进行磁场测量的，而氦原子自旋磁矩的极化是通过与已经被光学泵浦铯原子发生潘宁磁撞和自旋交换磁撞来完成的。

由于亚稳态氦原子含有19.82eV的能量，远高于铯原子的电离能3.89eV，当二者发生碰撞时，有很大的概率会发生潘宁电离。

需要说明的是，该理论值利用了实测线宽作为估算y的数据，必定包含了一些如周围磁场波动、光背景扰动等在更精密的实验条件下可以规避的退极化率，因此该γ值的估算是偏大的，也就是说此处得到的铯氦粒子数比值NCs≈1.9NHe可以作为最佳比值的一个上限值。

2实验

2.1铯-氦磁强计实验装置

为了研究铯-氦磁强计探头中铯氦粒子数的最佳比值，需要搭建一套铯-氦磁强计实验装置，测量在磁共振信号幅度最优化时的信号线宽△f，和通过反向拓延得到的最小线宽△f1，得到亚稳态氦原子的退极化率γ，并独立测量铯原子和亚稳态氦原子的粒子数密度值NCs和NHe，与理论计算结果进行比较。

本文利用895nmdBR激光泵浦搭建了一套铯-氦光泵磁强计实验装置，如图1所示。激光经隔离、矫形、纯化为圆偏振光后，作为泵浦光源射入铯-氦气室探头内。铯-氦气室被放置在一个5层坡莫合金磁屏蔽筒中，筒内剩磁小于1nT。在探头上放置有激励亚稳态氦原子的激励电极，通过施加载波为50mHz，重复频率1kHz的脉冲微波对气室进行激励，脉冲宽度可以在1-100μs调节。探头上沿垂直于泵浦光传播的方向放置了用于扫描磁共振信号的交变磁场线圈。磁屏蔽筒纵向放置了一个可以产生0.1mT以内标准磁场的加勒特线圈。

铯-氦光泵磁强计的工作过程为：首先通过圆偏振激光激励cs（6²S1/2→6²P_1/2）跃迁，将光子的角动量传递给铯原子，使其最终基态最外层电子自旋分布极化。同时施加脉冲激励产生亚稳态氦He（2³S1），通过铯-氦原子之间的潘宁碰撞和自旋交换碰撞过程，将自旋极化传递给氦原子，使其产生宏观可观测磁矩M=NHe

2.2实验结果及分析

图2为经锁相放大器检波后输出的90度相位差的磁共振信号，其中心过零点即为磁共振点，对应的频率值即为拉莫尔频率，最大值和最小值间距为磁共振信号半线宽。

从图中磁共振信号可以看出，实测线宽为△f=（1560+20）Hz。该线宽是在信号幅值和线宽比值达到最大，即灵敏度最高的状态下测得的。

线宽和泵浦光强、交变磁场调制频偏和交变磁场振幅都有关系。通过反向拓延法不断减小调制幅度和调制频偏，可以找到不受射频展宽影响的磁共振信号的线宽，见图3。

图3中，不同颜色的实线代表了不同交变磁场的幅值Brf，雪花状的点为实验测量值，带颜色的实线为根据实验测量值所做的线性拟合曲线。空心圆点为交变磁场幅值Brf=0mV时的线宽值。由于交变磁场为零时信号衰减为零，因此空心圆点表示的线宽值由该点所在横坐标上的彩色雪花点（测量值）反向拓延得到。黑色虚线为依据空心圆点代表的Brf=0mV时不同频偏下的线宽值所做的线性拟合函数，黑色虚线与y轴的交点，即代表调制幅度Brf和调制频偏都为0时，磁共振信号的线宽，为114Hz。

考虑到测量误差，该反向拓延的线宽值与理论值104Hz已经相当吻合。从图2和图3的数据可以估算出亚稳态氦原子的退极化率γ=15，见式（10）。

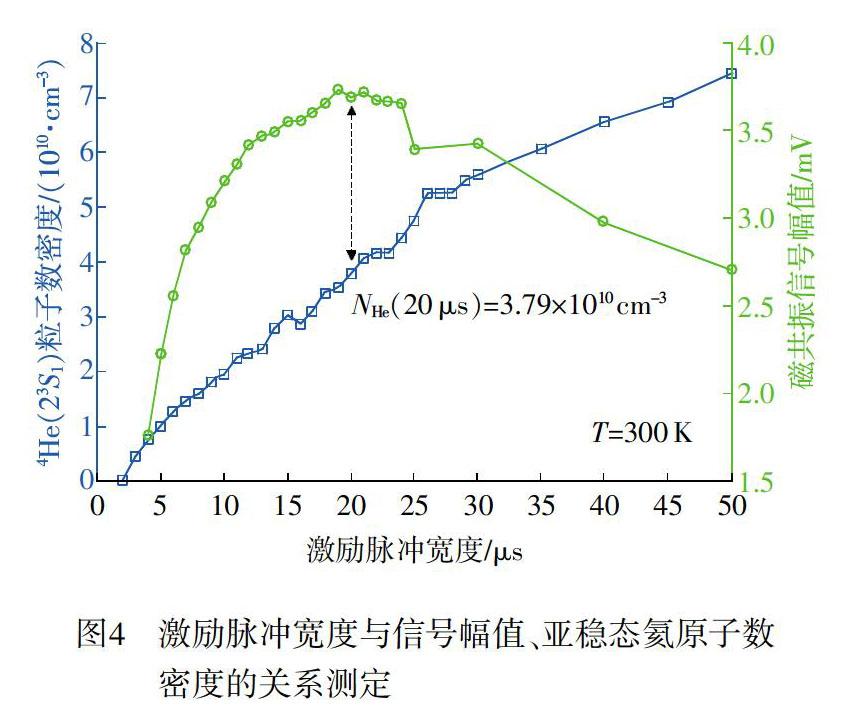
為了测量铯氦粒子数最佳配比值，实验上可以通过改变铯-氦气室温度调节铯原子的粒子数密度，通过改变脉冲激励的脉冲宽度调节氦粒子数密度。在某恒定温度点，通过改变脉冲宽度找到使磁共振信号灵敏度最大的点，得到最佳脉冲宽度，然后分别测量铯氦粒子数密度。

在图4中的绿色圆线为温度27℃（300k）时信号幅值与脉冲宽度的关系，可以看出，在20μs时，信号幅值达到最大。

再利用另一台1083nm半导体激光器，通过测量不同脉冲宽度下的亚稳态氦粒子对激光的吸收谱，可以得到亚稳态氦粒子数密度与脉冲宽度的关系，见图4中的蓝色方线。

可以看出在温度为27℃，脉冲宽度为20μs时，信号幅值达到最大，而该脉冲宽度对应亚稳态氦原子数密度为3.79×10¹⁰cm^-2。而在27℃，通过克拉伯龙方程，可知铯原子的粒子数密度为6.126×101¹⁰cm^-3，于是有NCs：NHe≈1.6：1。

需要说明的是，实际测量时气室内由脉冲激励激发的高能粒子对气室有一定加热效应，在外壁测量到的气室温度可能比气室中心气体温度低1℃左右，所以实测的粒子数比值中cs原子粒子数密度可能有所低估，因此实验测得的铯氦粒子数比值NCs：NHe≈1.6：1可以作为一个最优比值的下限值。

考虑到从线宽估算退极化率的误差和实验测量气室温度的误差，此处得到的铯氦粒子数最佳比值的理论值和实验值已经较为吻合。由于计算理论值时，对退极化率的估计偏大，因此理论比值NCs≈1.9NHe是一个上限值。实验中，由于对气室中心温度测量值偏小，导致对铯的粒子数密度值估算偏小，所以实测最佳比值NCs≈1.6NHe是一个下限值，因此在铯-氦光泵磁强计气室中铯氦的粒子数密度最佳比值应该介于二者之间。

3结束语

本文通过对铯-氦混合气体潘宁电离和自旋交换碰撞过程的分析，理论上给出了铯-氦磁强计的最佳粒子数比值NCs≈1.9NHe；同时搭建了一套铯-氦磁强计系统，在达到最优化的磁共振信号的条件下，测量了铯氦粒子数实际比值为NCs≈1.6NHe。通过分析理论值和实测值的成立条件，可以得到铯-氦粒子数最佳比值介于1.6～1.9之间。本工作的结论可以为铯氦光泵磁强计工作在不同环境温度下时得到最佳磁测量信号提供理论基础和实验参考数据。