基于误差信号反馈的单相LCL型逆变器谐振抑制方法
万晓凤 聂晓艺 廖志鹏 丁小华 曾繁鹏

摘 要:LCL滤波器可对逆变器输出电流所包含的高频谐波产生显著的衰减效果,但其本身的三阶谐振特性容易影响系统的稳定性。针对该问题,在传统单相LCL型并网逆变器并网电流反馈控制方法和电网电压比例前馈控制策略的基础上,提出了一种基于误差信号反馈的新型控制策略,首先根据L滤波器和LCL滤波器在低中频范围内频率特性基本一致的特点,估计出LCL滤波器谐振峰被抑制后的输出电流,而后将实际电流与估计值之差反馈到控制回路中以抑制谐振。从理论上分析了该方法对系统稳定性的影响,并给出相应参数的设计方法,最后通过仿真和实验结果验证了所提控制策略的正确性和有效性。
关键词:LCL滤波器;电网电压前馈;误差反馈;谐振抑制
中图分类号:TM 464
文献标志码:A
文章编号:1007-449X(2018)05-0102-08
Abstract:LCL filter has a significant attenuation effect on high frequency harmonics contained in the output current of the inverter, but its own thirdorder resonance characteristics easily affect the stability of the system. To solve this problem, an error signal feedback control method was proposed on the basis of the traditional current feedback control method and grid voltage feedforward control strategy for LCLtype inverter. Firstly, the output current when the resonant peak of LCL filter has been suppressed was estimated based on the fact that LCL filter has the same frequency characteristics with L filter in low frequency range, and then the difference between the actual current and the estimated value was fed back to suppress resonance. The influence of the method on the stability of the system was analyzed, and the parameter design method was provided. Finally, the simulation and experimental results verify effectiveness of the proposed control strategy.
Keywords:LCL filter; grid voltage feedforward; error feedback; resonance suppression
0 引 言
隨着全球能源危机的加剧,可再生能源的开发受到了越来越广泛的关注,作为清洁能源利用的主要方式之一,并网发电逆变技术也备受重视。在逆变过程中,受开关功率器件工作特性的影响,逆变器输出电压和电流具有大量的谐波,所以需要在逆变器和电网之间串入滤波器以抑制谐波,使输出电流满足相应的并网标准,常用的滤波器有L滤波器、LC滤波器和LCL滤波器,与前两者相比,LCL滤波器具有更好的高频谐波抑制性能,在滤波效果相同的前提下能够减小滤波器的体积和成本,因而得到了广泛的应用[1-2]。
尽管LCL滤波器的滤波效果更为明显,但LCL滤波器本身是一个三阶谐振电路[3-5],其输出电流在谐振频率处带有大量的谐波,且相位穿越-180°,很容易影响并网电流的电能质量及系统的稳定性,所以需采取阻尼措施使系统保持稳定[6]。常用的阻尼方法有无源阻尼法[7-9]和有源阻尼法[10-12],无源阻尼法通过在滤波器支路中串入电阻实现,能够显著的抑制LCL滤波器的谐振特性及提高系统的稳定性,然而有能量损耗,不利于提高逆变效率,文献[8-9]提出了基于分裂电容的无源阻尼控制策略,将LCL滤波器的滤波电容分为两部分且只在其中一个电容上串联电阻,相比完全电容阻尼方案能够减小功率损耗,但不能完全避免;有源阻尼法通过改变控制结构以抑制谐振,常用的“虚拟电阻法”通过引入LCL滤波器某一支路的状态变量反馈达到控制目标,文献[10-12]引入电容电流比例反馈,能够有效抑制LCL谐振峰,由于电路中没有串入无源元件,因此不会造成额外的损耗,但是此方法需要增加额外的传感器,不利于节约成本。
本文在传统的并网电流反馈及电网电压前馈控制方法的基础上,提出了一种基于误差信号反馈的新型控制策略。首先估计出LCL滤波器谐振峰被抑制后的输出电流,再将实际电流与估计值之差反馈到控制回路中以抑制谐振。由于该方法无需在电路中串入无源阻尼或增加传感器,因而不会产生额外的能量损耗及成本。仿真和实验结果验证了所提出控制策略的正确性和有效性。
1 系统数学模型
1.1 逆变器拓扑
单相LCL型并网逆变器的系统结构如图1所示,开关管Q1~Q4组成单相逆变器全桥结构,udc为逆变器输入端电压,由前端电源提供,ui为逆变器输出电压,ug为电网电压。电感L1、L2与电容C组成LCL滤波器,Lg为电网阻抗,系统通过调节开关管的通断时间以调节逆变器输出电压,从而达到控制输出电流的目的。
1.2 传统并网控制策略及稳定性分析
根据图1,得到考虑电网阻抗情况下LCL滤波器的等效数学模如图2所示。
图3为传统控制策略下单相LCL型逆变器的控制框图,其中GLCL-Lg(s)为考虑电网阻抗情况下LCL滤波器的传递函数,Gpi1(s)为并网电流控制器,即
为减小电网电压对系统稳态误差的影响,引入电网电压前馈[13],其中kpwm=udc,为PWM逆变器在开关频率足够高的情况下的等效比例增益[14]。
忽略电网电压干扰项ug,根据图2和图3,求得系统的开环传递函数为
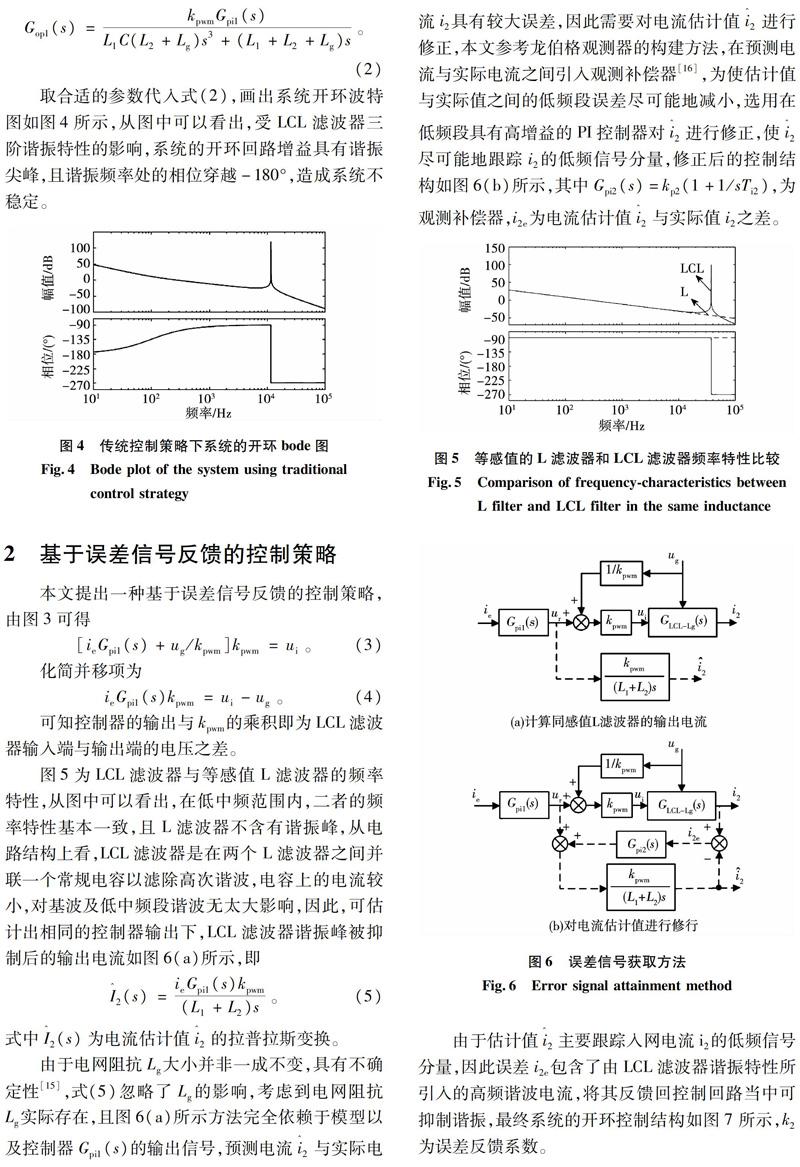
取合适的参数代入式(2),画出系统开环波特图如图4所示,从图中可以看出,受LCL滤波器三阶谐振特性的影响,系统的开环回路增益具有谐振尖峰,且谐振频率处的相位穿越-180°,造成系统不稳定。
2 基于误差信号反馈的控制策略
可知控制器的输出与kpwm的乘积即为LCL滤波器输入端与输出端的电压之差。
图5为LCL滤波器与等感值L滤波器的频率特性,从图中可以看出,在低中频范圍内,二者的频率特性基本一致,且L滤波器不含有谐振峰,从电路结构上看,LCL滤波器是在两个L滤波器之间并联一个常规电容以滤除高次谐波,电容上的电流较小,对基波及低中频段谐波无太大影响,因此,可估计出相同的控制器输出下,LCL滤波器谐振峰被抑制后的输出电流如图6(a)所示,即
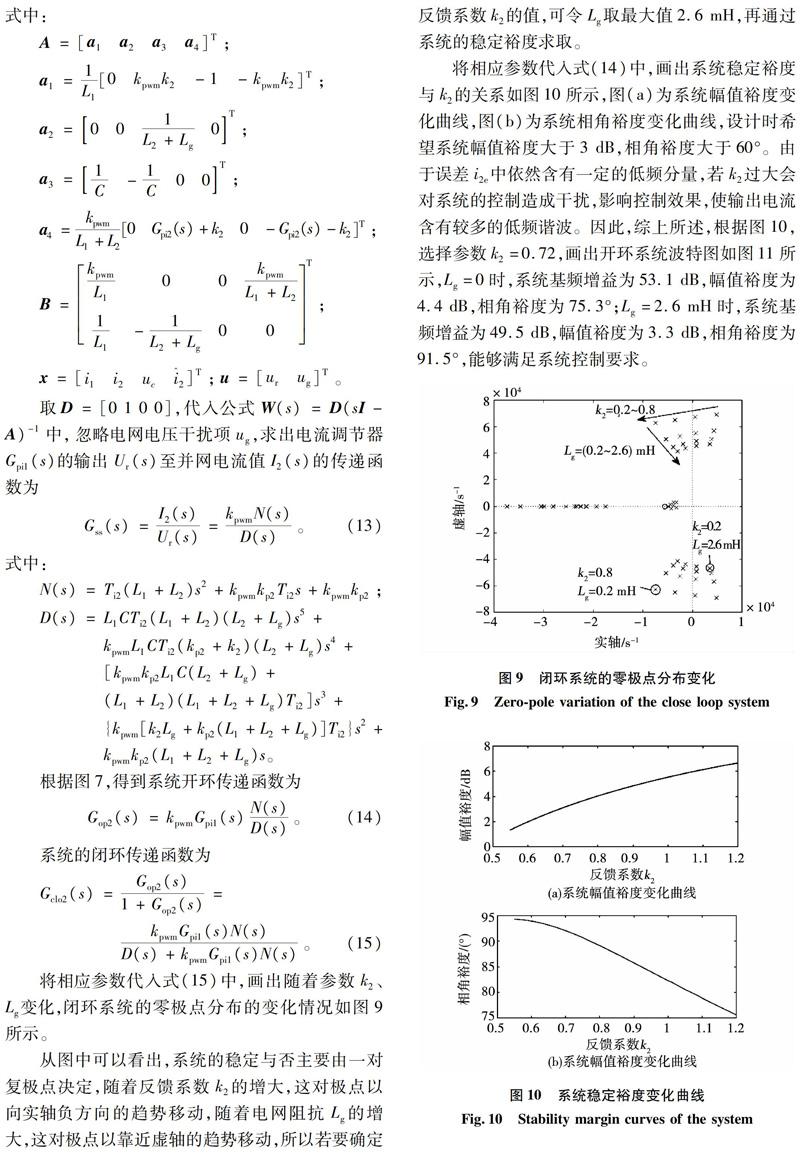
从图中可以看出,系统的稳定与否主要由一对复极点决定,随着反馈系数k2的增大,这对极点以向实轴负方向的趋势移动,随着电网阻抗Lg的增大,这对极点以靠近虚轴的趋势移动,所以若要确定反馈系数k2的值,可令Lg取最大值2.6 mH,再通过系统的稳定裕度求取。
将相应参数代入式(14)中,画出系统稳定裕度与k2的关系如图10所示,图(a)为系统幅值裕度变化曲线,图(b)为系统相角裕度变化曲线,设计时希望系统幅值裕度大于3 dB,相角裕度大于60°。由于误差i2e中依然含有一定的低频分量,若k2过大会对系统的控制造成干扰,影响控制效果,使输出电流含有较多的低频谐波。因此,综上所述,根据图10,选择参数k2=0.72,画出开环系统波特图如图11所示,Lg=0时,系统基频增益为53.1 dB,幅值裕度为4.4 dB,相角裕度为75.3°;Lg=2.6 mH时,系统基频增益为49.5 dB,幅值裕度为3.3 dB,相角裕度为91.5°,能够满足系统控制要求。
4 仿真与实验结果
根据图1中逆变器拓扑以及本文所示控制框图,在Matlab/SIMULINK环境中搭建单相LCL型并网逆变器的仿真模型,系统仿真参数如表1所示。
图12为使用传统控制策略得出的仿真波形,可以看出,采用传统的PI控制策略,逆变器输出电流发散,控制系统发生谐振,无法正常运行。
图13为使用本文所提出控制策略的系统仿真结果,为便于观察,将误差i2e放大10倍显示,对比图13(a)和图13(b)可知,使用本文提出的控制策略能够使系统稳定运行,但需要合理设置反馈系数k2的值,才能保证并网电能质量;对比图13(b)和图13(c),相对于图13(b)来说,可以看出图13(c)中误差i2e含有更多的基频分量,可知电网阻抗会影响入网电流的估计值,不过通过合理地设置补偿器Gpi2(s)的参数,能够降低电网阻抗带来的影响,保证系统在稳定可靠的范围内运行。
图14为在阶跃扰动下系统的仿真波形,其中电网阻抗Lg=2.6 mH,反馈系数k2=0.72,从图中可以看出,在阶跃扰动过程中,入网电流经过微小的超调之后能够迅速跟踪指令电流,因而系统具有良好的稳定性。
为进一步验证控制策略的有效性,搭建了一台200 W的单相LCL型微逆变器样机进行实验。实验参数:逆变侧电感5 mH,滤波电容0.22 μF,电网侧电感1 mH,开关频率50 kHz,直流母线电压300 V,逆变器接入110 V/50 Hz的模拟电网,在LCL滤波器后面接入2.6 mH的电感模拟电网阻抗。实验波形如图15所示,图15(a)和图15(b)分别为取k2=0.5和k2=0.7时的电网电压和并网电流波形。k2取0.5时,并网电流的总谐波含量为7.3%,k2取0.7时,并网电流的总谐波含量为3.4%,通过对比可知,引入误差信号反馈之后能够抑制LCL滤波器谐振,而在一定范围内提高反馈系数,能够进一步地改善并网电能质量,图15(c)为阶跃信号下的输出电流波形,系统在经过微小的超调后能够迅速趋于稳定,因而具有良好的稳定性。
5 结 论
本文主要研究了单相LCL型并网逆变器的控制策略,通过建模和分析得知电网电压对系统存在扰动作用,需要引入电网电压前馈抑制扰动,而后在传统并网电流控制方法和电网电压比例前馈的基础上,提出了一种基于误差信号反馈的谐振抑制策略,首先估计出LCL滤波器谐振峰被抑制后的输出电流,而后将入网电流与估计值之差反馈到回路中以抑制谐振。本文通过建立系统的数学模型分析了系统的稳定性,并给出了合理的参数设计,最后通过仿真和实验验证了本文结论的有效性。
参 考 文 献:
[1] REZNIKA, SIMOES M G, AlDURRA A, et al. LCL filter design and performance analysis for gridinterconnected systems[J]. IEEE Transactions on Industry Applications,2014,50(2):1225.
[2] SHEN Guoqiao, ZHU Xuancai, ZHANG Jun, et al. A new feedback method for pr current control of LCLfilterbased gridconnected inverter[J]. IEEE Transactions on Industrial Electronics, 2010, 57(6): 2033.
[3] SHI Xiaojie, WANG Zhiqiang, MA Yiwei, et al. Modeling and control of an LCL filter based threephase active rectifier in grid emulator[C]//Applied Power Electronics Conference and Exposition. IEEE, 2013: 992-998.
[4] 江渝, 姜琦, 黄敏,等. 单相单级光伏LCL并网逆变系统控制策略[J]. 电网技术, 2015, 39(2): 312.
JIANG Yu, JIANG Qi, HUANG Min, et al. Control strategy of singlephase singlestage LCL gridconnected photovoltaic inverter system[J]. Power System Technology, 2015, 39(2): 312.
[5] 齐虹, 苏忠钰, 陈冲. 带LCL滤波的SAPF电流控制点选取的研究[J]. 电机与控制学报, 2016, 20(4):1.
QI Hong, SU Zhongyu, CHEN Chong. Research on selection of feedback currents for LCLfilterbased shunt APF[J]. Electric Machines and Control, 2016, 20(4): 1.
[6] DANNEHL J,FUCHS F W,THGERSEN P B. PI state space current control of gridconnected PWM converters with LCL filters[J].IEEE Transactions on Power Electronics,2010,25(9):2320.
[7] 张承慧, 叶颖, 陈阿莲,等. 基于输出电流控制的光伏并网逆变电源[J]. 电工技术学报, 2007, 22(8):41.
ZHANG Chenghui, YE Ying, CHEN Alian, et al. Research on gridconnected photovoltaic inverter based on output current control[J]. Transactions of China Electrotechnical Society, 2007, 22(8): 41.
[8] 王海松, 王晗, 张建文,等. LCL型并网逆变器的分裂电容无源阻尼控制[J]. 电网技术, 2014, 38(4): 895.
WANG Haisong, WANG Han, ZHANG Jianwen, et al. Splitcapacitor passive damping control for LCL gridconnected inverter[J]. Power System Technology, 2014, 38(4): 895.
[9] WU Weimin, HE Yuanbin, TANG Tianhao, et al. A new design method for the passive damped LCL and LLCL filterbased singlephase gridtied inverter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(10): 4339.
[10] XU Jinming, XIE Shaojun, TANG Ting. Improved control strategy with gridvoltage feedforward for LCLfilterbased inverter connected to weak grid[J]. Power Electronics Iet, 2014, 7(10): 2660.
[11] PENG Shuangjian, LUO An, CHEN Yandong, et al. DualLoop power control for singlephase gridconnected converters with LCL filter[J]. Journal of Power Electronics, 2011, 11(4): 456.
[12] 徐志英, 许爱国, 谢少军. 采用LCL滤波器的并网逆变器双闭环入网电流控制技术[J]. 中国电机工程学报, 2009, 7(27): 36.
XU Zhiying, XU Aiguo, XIE Shaojun. Dualloop grid current control technique for Gridconnected inverter using an LCL filter[J]. Proceedings of the CSEE, 2009, 7(27): 36.
[13] 鲍陈磊, 阮新波, 王学华,等. 基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J]. 中国电机工程学报, 2012, 32(25): 133.
BAO Chenlei, RUAN Xinbo, WANG Xuehua, et al. Design of gridconnected inverters with lcl filter based on PI regulator and capacitor current feedback active damping[J]. Proceedings of the CSEE, 2012, 32(25): 133.
[14] 吴云亚, 谢少军, 阚加荣,等. 逆变器侧电流反馈的LCL并网逆变器电网电压前馈控制策略[J]. 中国電机工程学报, 2013, 33(6): 54.
WU Yunya, XIE Shaojun, KAN Jiarong, et al.A full grid voltage feedforward control strategy with inverterside current feedback for LCL gridconnected inverters[J]. Proceedings of the CSEE, 2013, 33(6): 54.
[15] 王萍, 蔡蒙蒙, 王尉. 基于自适应陷波滤波器的有源阻尼控制方法[J]. 电机与控制学报, 2015, 19(9): 108.
WANG Ping, CAI Mengmeng, WANG Wei. Adaptive notch filter based active damping control method[J]. Electri c Machines and Control, 2015, 19(9): 108.
[16] Ellis G,汤晓君. 控制系统设计指南(第三版)[M]. 机械工业出版社, 2006: 146-147.
(编辑:张 楠)

