基于灰度图像分解的局部放电特征提取与优化

汪可 张书琦 李金忠 孙建涛 赵晓宇 廖瑞金 邹国平

摘 要：提取有效的局部放电（PD）特征是输变电设备缺陷识别的前提。以局部放电灰度图像为分析对象，提出了基于二维主成分分析（2DPCA）的局部放电图像特征提取策略。算法通过2DPCA将PD灰度图像分解为多个一维向量，并对每个向量提取了9个特征参量，组成了PD图像分解特征集。同时，建立了基于粒子群优化（PSO）算法的PD特征选择算法，以优化PD图像分解特征，提升局部放电缺陷类型识别结果。对实验室考虑多因素影响的PD样本识别结果表明，2DPCA图像分解特征可以取得93%的PD缺陷识别率，经过PSO优化后的2DPCA特征可以将PD识别率提高至96%，并且特征维数由72降至28，充分说明方法的有效性。另外，对添加不同随机干扰的PD样本平均识别率均大于85%，表明2DPCA图像特征具有较好的抗随机干扰能力。

关键词：局部放电；模式识别；图像分解；特征提取；特征选择；模糊k近邻

中图分类号：TM 835

文献标志码：A

文章编号：1007-449X（2018）05-0025-10

Abstract：Effective features extraction of partial discharge （PD） is the foundation of defect identification of electrical apparatus. Using PD gray image as the analysis object， a PD image features extraction strategy was proposed based on twodimensional principal component analysis （2DPCA）. Various 1dimensional （1D） vectors were obtained by implementing 2DPCA on PD gray images in the proposed method. 9 characteristic parameters were extracted from each 1D vector， which constituted the PD image decomposition features. In addition， a PD features selection algorithm was developed based on particle swarm optimization （PSO） algorithm， which attempts to optimize the extracted PD image decomposition features and improve the PD recognition accuracy. The recognition results of PD samples considering the multifactor influences in laboratory illustrate that the proposed 2DPCA image decomposition features can achieve the high PD recognition accuracy of 93%. Besides， the PSO optimized 2DPCA features can further improve the PD recognition accuracy to 96% and simultaneously reduce the feature dimension from 72 to 28， which fully demonstrates effectiveness of the proposed algorithm. Moreover， the average recognition accuracies of PD samples added with different random noises are all higher than 85%， which indicates that 2DPCA image features possess good tolerance ability of random noises.

Keywords：partial discharge； pattern recognition； image decomposition； feature extraction； feature selection； fuzzy knearest neighbor

0 引 言

局部放電（partial discharge，PD）是导致变压器油纸绝缘劣化的主要原因之一[1]。变压器在生产、运输和安装过程中不可避免地出现潜伏性缺陷，并在长期运行中逐渐扩大，当电场畸变严重时会产生局部放电。随着输电电压等级和容量的不断提高，局部放电监测和分析成为电力变压器状态评估中最重要的技术手段[2-3]。

近年来，国内外在电气设备局部放电的特征提取识别方面开展了大量的研究工作。基于最常用的时间分布和相位分布，形成了多种具有代表性的局部放电特征，包括统计特征[4]、Weibull参数[5]、小波系数[6]、图像分形特征[7]、波形特征[8]等。同时，基于机器学习的分类技术被广泛应用于局部放电诊断中，如模糊C-均值聚类[9]、距离分类器[10]、模糊逻辑分类器[11]、人工神经网络[12]和支持向量机[13]等。与分类器相比，局部放电特征的优劣直接决定了PD识别结果的准确性。若提取的特征难以真实反映不同类型局部放电之间的区别，那么采用任何一个分类器也难以进行有效识别。相反，采用鉴别力强的PD特征结合最简单的线性分类器则可以取得较好的识别结果[14]。因此，特征提取是局部放电分析与诊断研究中最重要的部分。

随着计算技术的飞速发展，基于数字信号处理的时频分析[15-16]和图像分析方法[17-18]也被用于局部放电特征提取中。灰度图像是局部放电缺陷识别中常用的表征方法之一，通常以多个工频周期的局部放电相位和脉冲幅值数据，在相位-幅值二维平面内统计单位像素点内的放电脉冲个数进行灰度计算得到局部放电灰度图像。以分维数和空缺率为代表的分形特征是分析局部放电灰度图像的主要技术手段[19-22]。值得注意的是，以往的PD特征提取与模式识别技术均采用实验室典型缺陷的数据进行验证；然而实验室采集的大部分局部放电样本并未考虑絕缘老化、缺陷尺寸、施加电压等多因素的影响，降低了局部放电识别的可靠性[23]。

本文以局部放电灰度图像为分析对象，提出一种基于二维主成分分析（twodimensional principal component analysis， 2DPCA）图像分解的局部放电特征提取方法，并设计粒子群优化（particle swarm optimization， PSO）算法对提取的局部放电图像特征进行优选。最后采用考虑绝缘老化、缺陷尺寸、施加电压等多因素影响的局部放电样本对算法的有效性进行了验证，并与常用的局部放电PRPD等方法进行了对比。

1 局部放电灰度图像样本

1.1 人工缺陷模型及局部放电样本

参照以往研究采用典型的油纸绝缘缺陷模型进行局部放电试验[24-26]，包括：绝缘纸板内部气隙放电（G）、油中沿面放电（S）、油中电晕放电（C）、油/空气分界面放电（I）。在试验时，考虑绝缘老化、缺陷尺寸、施加电压的影响，采用老化14天和42天的绝缘纸板来构造不同缺陷尺寸的局部放电缺陷模型，并在多个电压下采集局部放电样本，得到G类放电125个样本、S类放电122个样本、C类放电94个样本和I类放电78个样本，共419个样本，缺陷模型详细结构、PD样本信息和试验回路详见文献[23]。

1.2 局部放电信号预处理及灰度图像构造

通过数字化测量系统采集的局部放电信号不可避免地会包含一定的噪声。为了准确获取人工缺陷模型的局部放电脉冲幅值和相位数据，本文采用小波分析[29]结合阈值去噪的方法对局部放电原始数据进行预处理。

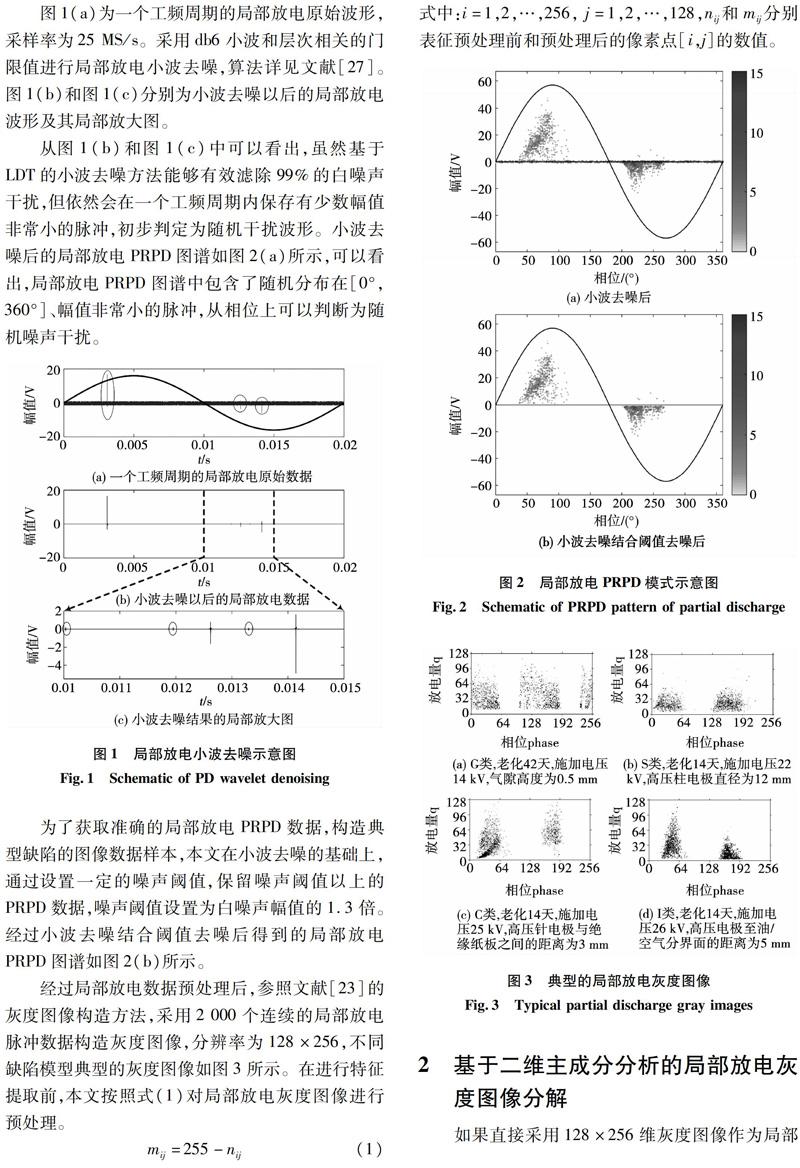
图1（a）为一个工频周期的局部放电原始波形，采样率为25 MS/s。采用db6小波和层次相关的门限值进行局部放电小波去噪，算法详见文献[27]。图1（b）和图1（c）分别为小波去噪以后的局部放电波形及其局部放大图。

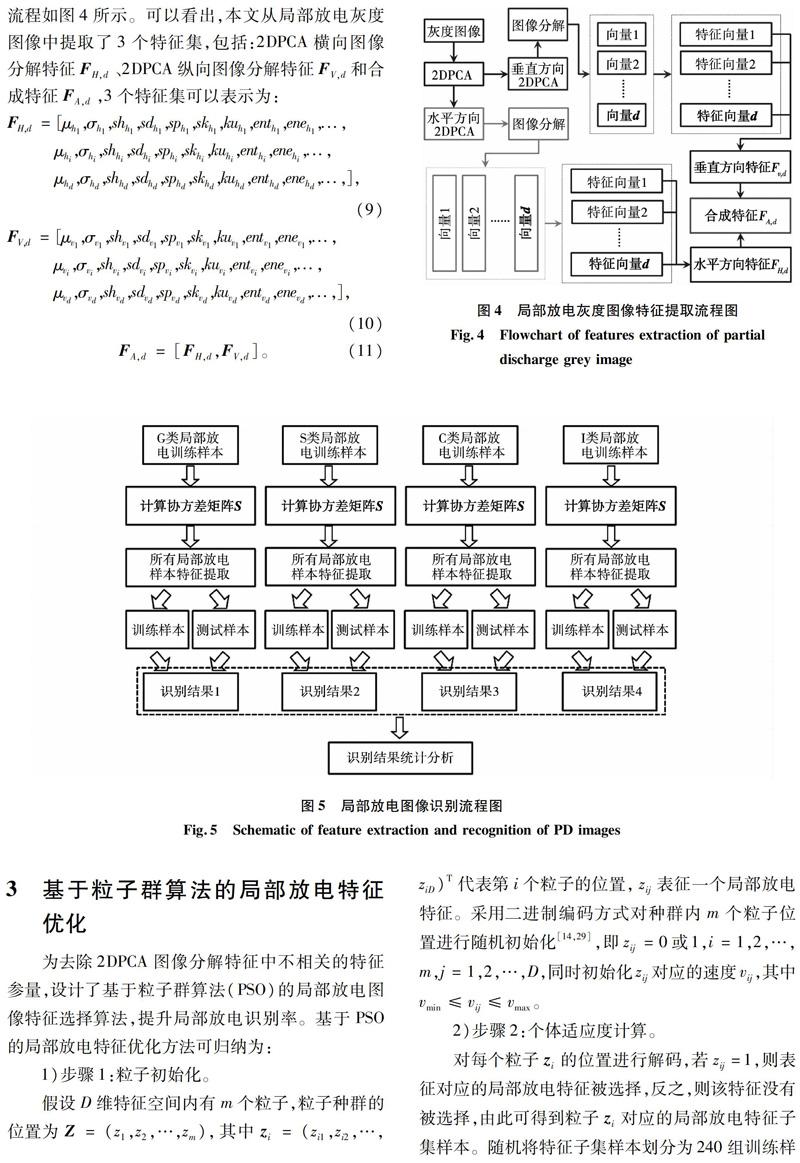
从图1（b）和图1（c）中可以看出，虽然基于LDT的小波去噪方法能够有效滤除99%的白噪声干扰，但依然会在一个工频周期内保存有少数幅值非常小的脉冲，初步判定为随机干扰波形。小波去噪后的局部放电PRPD图谱如图2（a）所示，可以看出，局部放电PRPD图谱中包含了随机分布在[0°， 360°]、幅值非常小的脉冲，从相位上可以判断为随机噪声干扰。

为了获取准确的局部放电PRPD数据，构造典型缺陷的图像数据样本，本文在小波去噪的基础上，通过设置一定的噪声阈值，保留噪声阈值以上的PRPD数据，噪声阈值设置为白噪声幅值的1.3倍。经过小波去噪结合阈值去噪后得到的局部放电PRPD图谱如图2（b）所示。

经过局部放电数据预处理后，参照文献[23]的灰度图像构造方法，采用2 000个连续的局部放电脉冲数据构造灰度图像，分辨率为128×256，不同缺陷模型典型的灰度图像如图3所示。在进行特征提取前，本文按照式（1）对局部放电灰度图像进行预处理。

2 基于二维主成分分析的局部放电灰度图像分解

如果直接采用128×256维灰度图像作为局部放电样本数据库进行缺陷类型识别，不仅图像样本数据存储量非常大，而且分类器难以直接对图像样本进行训练和识别，需要提取灰度图像特征，并构造局部放电特征指纹库。降维是图像特征提取的主要方法之一，被广泛用于人脸识别。本文采用2DPCA方法对局部放电灰度图像进行降维处理，分别从横向和纵向实现灰度图像分解，并对每一个图像分解向量提取一系列特征，构造局部放电的图像特征集。

2.1 二维主成分分析

与针对一维向量的主成分分析不同，2DPCA直接计算二维图像矩阵的协方差矩阵，不仅具有更高的计算效率，而且可以保存原始图像的结构信息[28]。

3 基于粒子群算法的局部放电特征优化

为去除2DPCA图像分解特征中不相关的特征参量，设计了基于粒子群算法（PSO）的局部放电图像特征选择算法，提升局部放电识别率。基于PSO的局部放电特征优化方法可归纳为：

5）步骤5：重复步骤2～4，直至迭代次数t达到最大迭代次数T为止，并对具有最高个体适应度的粒子位置进行解码，得到优化后的局部放电特征子集。

4 实验结果分析与讨论

4.1 局部放电图像特征提取与识别

为了更系统地分析本文方法的有效性，分别采用单一缺陷的样本（M=60）计算协方差矩阵S提取所有局部放电样本的特征，并进行归一化处理，然后将样本划分为训练样本和测试样本，进行局部放电识别结果分析，整个流程图如图5所示。

4.2 投影轴数d对识别结果的影响

分别选择d=1，2，3，4对419组样本提取2DPCA图像分解特征，并随机将419个局部放电样本划分为240个训练样本（每类60个样本）和179个测试样本，共划分50次。采用FkNNC对测试样本进行识别，FH，d、FV，d和FA，d的识别结果分别如图6（a）～图6（c）所示。

从图6可以看出，当d=1时，FV，d的识别率高于FH，d，而d=2～4时则相反。当d不同时，FA，d的识别结果比FH，d和FV，d要更好，并且当d=3，4时，FA，d的平均识别率均高于90%。进一步对不同缺陷样本提取的2DPCA特征识别结果进行统计，结果如表2所示。由表中数据可知，局部放电平均识别率随着投影轴数d的增加而逐渐增加，d=3～4时FH，d、FV，d和FA，d的识别效果均比d=1～2时要更好。从统计结果看，当d=3～4时，2DPCA图像分解特征可以取得约93%的局部放电识别率，充分说明了2DPCA图像分解特征具有较好的局部放电识别能力。

4.3 PSO优化特征的识别结果

为优化2DPCA图像分解特征，采用PSO对提取的特征进行选择，优选出具有更好识别效果的图像特征子集。PSO的算法参数如表3所示。

表4给出了d=1，2，3，4时PSO优选2DPCA特征的识别结果，图7给出了PSO在迭代过程中的适应度变化曲线。对比表2和表4的结果可以看出，当d取不同值时，PSO优选特征较原始2DPCA特征的识别结果均有不同程度的提高。当d=4时，PSO优选2DPCA特征能够取得96.40%的平均识別率，同时特征维数由72降至为28，表明PSO不仅能够提升2DPCA特征的识别率，同时也可以显著降低特征维数。表5给出了d=4时的PSO优选特征（以FA，4，P表征），其中▲表征该特征被选取，可以看出σ、sd和ene不具有识别局部放电缺陷类型的能力。

4.4 与2DPCA降维特征的对比

2DPCA作为一种图像降维方法广泛应用于人脸识别中，包括横向2DPCA、纵向2DPCA和双向2DPCA 3种典型的图像降维方法[34]。为了对比本文提取的2DPCA图像分解特征与2DPCA降维特征的识别效果，分别采用单一缺陷的样本（M=60）计算协方差矩阵S提取H2DPCA、V2DPCA和（2D）2PCA降维特征，投影轴数d=1～4。按照上文所述的训练样本和测试样本随机划分方法，计算2DPCA降维特征的局部放电样本的识别率，结果表明当d=4时，2DPCA降维特征的识别效果最好，如表6所示。由表中数据可知，2DPCA降维特征的识别结果略低于2DPCA图像分解特征FA，d和PSO优选2DPCA图像分解特征FA，4，P。

4.5 与其他局部放电识别方法的对比

为了进一步验证本文方法的有效性，基于试验采集的局部放电样本，对比分析PSO优选2DPCA图像分解特征FA，4，P与其他局部放电识别方法的识别结果。

首先，直接从局部放电灰度图像中提取表1所示的特征，先进行“2D图像→1D向量”变换，将128×256维灰度图像横向拉直为1×32768维向量和纵向拉直为32768×1维向量，然后对每个1×32768维向量和32768×1维向量提取9个特征，分别记为FI，H和FI，V。其次，局部放电相位分布（phaseresolved partial discharge， PRPD）统计特征是局部放电识别最常用的方法，本文提取4种常见的局部放电PRPD图谱的27个统计特征，其物理意义详见文献[29]。此外，文献[23]提出了基于模糊理论和图像双向压缩的双向模糊加权二维线性鉴别分析方法，对典型局部放电缺陷的识别结果验证了TDFW2DLDA方法的有效性。

本文采用FkNNC对PSO优选2DPCA图像分解特征FA，4，P、图像直接提取特征FI，H和FI，V、TDFW2DLDA特征、PRPD统计特征的识别结果如表7所示，可以看出本文提出的FA，4，P具有更好的局部放电识别效果。

表8给出了分别采用FkNNC、反向传播神经网络[29]和支持向量机[23]对PSO优选2DPCA特征的识别结果。可以看出，SVM的识别结果比FkNNC和BPNN更好，FkNNC的识别率略低于SVM。从识别时间上看，FkNNC不需要进行分类器训练，识别时间仅为0.16 s，而BPNN和SVM的总识别时间分别为8.31 s和90.5 s。另外，当新增一种新的局部放电缺陷类别时，FkNNC可以在增加训练样本的同时直接进行识别，而BPNN和SVM需要重新进行分类器训练。因此，FkNNC可以兼顾识别率和计算效率两个方面，更适合进行局部放电缺陷类型识别。

4.6 随机噪声的影响

对局部放电样本添加5%～15%均匀分布在[0°，360°]范围内的随机噪声，噪声幅值分别为20pC、50pC和100pC。添加随机噪声后的PSO优选2DPCA特征的识别结果如表9所示，结果显示添加随机噪声后，局部放电样本的平均识别率均大于85%，表明本文提出的方法具有较好的抗随机噪声干扰能力。

5 结 论

1）提出了基于2DPCA的局部放电灰度图像分解方法，将灰度图像分解成横向图像压缩向量和纵向图像压缩向量，并对每个图像压缩向量提取了平均值μ、尖锐度sh等9个特征参量，组成了包含局部放电信息的2DPCA图像分解特征。对实验室油纸绝缘局部放电样本的识别结果表明，2DPCA图像分解特征能够取得93%的平均识别率。

2）提出了基于PSO的局部放电2DPCA图像分解特征优化策略。对实验室样本的识别结果表明，PSO不仅能够将局部放电的平均识别率从93%提升至96%，而且可以显著降低特征维数。相比原始2DPCA图像分解特征，PSO优选特征具有更好的识别效果。

3）与以往TDFW2DLDA特征和PRPD特征相比，PSO优选2DPCA特征能够取得更好的识别效果。同时，当对数据样本添加不同大小和数量的随机噪声时，PSO优选2DPCA特征的平均识别率依然大于85%，具有较好的抗随机干扰能力。

参 考 文 献：

[1] 魏新劳， 裴震， 聂洪岩， 等. 阶梯电压下变压器匝间绝缘局部放电试验研究[J]. 电机与控制学报， 2017， 21（7）： 49.

WEI Xinlao， PEI Zhen， NIE Hongyan， et al. Partial discharge tests and researches in power transformer interturn insulation under stepstress[J]. Electric Machine and Control， 2017， 21（7）： 49.

[2] 李军浩， 韩旭涛， 刘泽辉， 等. 电气设备局部放电检测技术述评[J]. 高电压技术， 2015， 41（8）： 2583.

LI Junhao， HAN Xutao， LIU Zehui， et al. Review on partial discharge measurement technology of electrical equipment[J]. High Voltage Engineering，2015， 41（8）：2583.

[3] 李金忠， 张乔根， 李原， 等. 油纸绝缘局部放电脉冲参数统计分析与老化状态诊断技术[J]. 高电压技术， 2015， 41（11）： 3821.

LI Jinzhong， ZHANG Qiaogen， LI Yuan， et al.Statistical analysis of pulse parameters and diagnose of aging state based on partial discharge in paperoil insulation[J]. High Voltage Engineering， 2015，41（11）： 3821.

[4] 赵学风， 蒲路， 琚泽立， 等. XLPE电力电缆附件局部放电测量与分析[J]. 电机与控制学报， 2016， 20（6）： 94.

ZHAO Xuefeng， PU Lu， JU Zeli， et al.Measurement and analysis of partial discharge of XLPE power cable accessories[J]. Electric Machine and Control， 2016， 20（6）： 94.

[5] CONTINA， CAVALLINI A， MONTANARI G C，et al. Digital detection and fuzzy classification of partial discharge signals[J]， IEEE Transaction on Dielectrics and Electrical Insulation， 2002， 9（3）：335.

[6] 唐炬， 樊雷， 张晓星， 等. 用谐波小波包变换法提取GIS局部放电信号多尺度特征参数[J]. 电工技术学报， 2015， 30（3）： 250.

TANG Ju， FAN Lei， ZHANG Xiaoxing， et al.Multiscale feature parameters extraction of GIS partial discharge signal with harmonic wavelet packet transform[J]. Transactions of China Electrotechnical Society， 2015， 30（3）： 250.

[7] GU F C， CHANG H C， CHEN F H， et al.Application of the HilbertHuang transform with fractal feature enhancement on partial discharge recognition of power cable joints[J]. IET Science Measurement & Technology， 2012， 6（6）： 440.

[8] OKUBOH， HAYAKAWA N. A novel technique for partial discharge and breakdown investigation based on current pulse waveform analysis[J]. IEEE Transaction on Dielectrics and Electrical Insulation， 2005， 12（4）： 736.

[9] 汪可， 廖瑞金， 吴高林， 等. 采用双向改进模糊2DLDA算法提升多因素影响的局部放电识别可靠性[J]. 电工技术学报， 2014， 29（11）： 210.

WANG Ke， LIAO Ruijin， WU Gaolin， et al. Improvement of partial discharge recognition reliability considering influence of multifactors based on twodirectional modified fuzzy 2DLDA algorithm[J].Transactions of China Electrotechnical Society， 2014，29（11）： 210.

[10] KRANZ H G. Diagnosis of Partial Discharge Signalsusing neural networks and minimum distance classification[J]. IEEE Transaction on Dielectrics and Electrical Insulation， 1993， 28（6）：1016.

[11] SALAMAM M A， BARTNIKAS R. Fuzzy logic applied to PD pattern classification[J]. IEEE Transaction on Dielectrics and Electrical Insulation， 2000， 7（1）： 118.

[12] 尚海昆， 苑津莎， 王瑜， 等. 基于交叉小波變换和相关系数矩阵的局部放电特征提取[J]. 电工技术学报， 2014， 29（4）： 274.

SHANG Haikun， YUAN Jinsha， WANG Yu， et al. Feature extraction for partial discharge based on crosswavelet transform and correlation coefficient matrix[J]. Transactions of China Electrotechnical Society， 2014， 29（4）： 274.

[13] 王瑜， 苑津莎， 尚海昆， 等. 組合核支持向量机在放电模式识别中的优化策略[J]. 电工技术学报， 2015， 30（2）： 229.

WANG Yu， YUAN Jinsha，SHANG Haikun， et al. Optimization strategy research on combinedkernel support vector machine for partial discharge pattern recognition[J]. Transactions of China Electrotechnical Society，2015， 30（2）： 229.

[14] WANGKe， LIAO Ruijin， YANG Lijun， et al. Optimal features selected by NSGAII for partial

discharge pulses separation based on timefrequency representation and matrix decomposition[J]. IEEE Transaction on Dielectrics and Electrical Insulation， 20（3）： 825.

[15] LUOG M， ZHANG D M， KOH Y， et al. Timefrequency entropybased partialdischarge extraction for nonintrusive measurement[J]. IEEE Transaction on Power Delivery， 2012， 27（4）：1919.

[16] LIAO Ruijin， WANG Ke， YANG Lijun， et al. Partial discharge signal classification utilizing timefrequency representation and two directional 2DPCA[J]. International Review on Electrical EngineeringIREE， 2012， 7（1）： 3358.

[17] WANG Ke， LIAO Ruijin， YANG Lijun， et al. Nonnegative matrix factorization aided principal component analysis for highresolution partial discharge image compression in transformers[J].International Review on Electrical EngineeringIREE， 2013， 8（1）： 479.

[18] WEI G，TANG J， ZHANG X X， et al. Gray intensity image feature extraction of partial discharge in highvoltage crosslinked polyethylene power cable joint[J]. International Transactions on Electrical Energy Systems， 2014， 24（2）： 215.

[19] SATISHL， ZAENGL W S. Can fractal features be used for recognizing 3D partial discharge patterns？[J].IEEE Transactions on Dielectrics and Electrical Insulation， 1995， 2（3）： 352.

[20] KRIVDA A，GULSKI E，SATISH L， et al. The use of fractal features for recognition of 3D discharge patterns[J]. IEEE Transactions on Dielectrics and Electrical Insulation， 1995， 2（5）：889.

[21] LI Jian，SUN Caixin，GRZYBOWSKI S， et al. Partial discharge image recognition using a new group of features[J]. IEEE Transactions on Dielectrics and Electrical Insulation， 2006， 13（6）：1245.

[22] LI Jian，SUN Caixin，GRZYBOWSKI S.Partial discharge image recognition influenced by fractal image compression[J]. IEEE Transactions on Dielectrics and Electrical Insulation， 2008， 15（2）： 496.

[23] WANG Ke， LI Jinzhong， ZHANG Shuqi， et al.Anew imageoriented feature extraction method forpartial discharges[J]. IEEE Transaction on Dielectrics and Electrical Insulation， 2015， 22（2）：1015.

[24] LIAO Ruijin， YAN Jiaming， YANG Lijun， et al.Study on the relationship between damage of oilimpregnated insulation paper and evolution of phaseresolved partial discharge patterns[J].European Transactions on Electrical Power， 2011，21（8）： 2112.

[25] LI J H， SI W R， YAO X， et al. Measurement andsimulation of partial discharge in oil impregnated pressboard with an electrical aging process[J].Measurement Science and Technology， 2009， 20（10）：105701.

[26] CAVALLINIA， MONTANARI G C， CIANI F.Analysis of partial discharge phenomena in paperoil insulation systems as a basis for risk assessment evaluation[C]//LIPLaboratrio de Instrumentao e Fsica Experimental de Partculas. IEEE International Conference on Dielectric Liquids， June 26-July 1， 2005， Coimbra， Portugal. Los Alamitos： IEEE， 2005： 241-244.

[27] MA X， ZHOU C， KEMP I J. Automated wavelet selection and thresholding for PD detection[J]. IEEE Electrical Insulation Magazine， 2002， 18（2）： 37.

[28] YANG J， ZHANG D， FRANGI A F， et al. Twodimensional PCA： a new approach to appearancebased face representation and recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence， 2004， 26（1）：131.

[29] LIAO Ruijin， WANG Ke， YANG Lijun. Binary particle swarm optimization selected timefrequency features for partial discharge signal classification[J]. International Review on Electrical EngineeringIREE， 2012， 7（5）： 5905.

[30] 汪可， 廖瑞金， 王季宇， 等. 局部放电UHF脉冲的时频特征提取与聚类分析[J]. 电工技术学报， 2015， 30（2）： 211.

WANG Ke， LIAO Ruijin， WANG Jiyu， et al. Timefrequency features extraction and clustering analysis of partial discharge UHF pulses[J].Transactions of China Electrotechnical Society， 2015， 30（2）： 211.

[31] GHORAANIB， KRISHNAN S. A joint timefrequency and matrix decomposition feature extraction methodology for pathological voice classification[J]. EURASIP Journal on Advances in Signal Processing， 2009： 10.

[32] KELLERJ M， GRAY M R， GIVENS J A. A fuzzy knearest neighbor algorithm[J]. IEEE Transactions on Systems， Man and Cybernetics， 1985， 15（4）： 580.

[33] YANG W K， YAN X Y， ZHANG L， et al.Featureextraction based on fuzzy 2DLDA[J].Neurocomputing，2010， 73（10-12）： 1556.

[34] ZHANG D Q， ZHOU Z H. （2D）2PCA： Two directional twodimensional PCA for efficient face representation and recognition[J]. Neurocomputing， 2005， 69（1-3）： 224.

（編辑：张 楠）