数字水准仪测量编解码技术研究

李学鹏　仲思东

摘要：针对传统的数字水准仪测量精度受到测量距离和视场的制约，固定的码元难以兼容远近测量的精度等问题，为进一步提高数字水准仪的测量精度，该文提出一种编解码方案，利用圆的各向同性性质，以圆形码代替传统条形码进行编制，并且采用面阵CCD获取二维编码图像，同时在远近不同距离采用不同进制编码，在解码粗测时应用最大相似匹配算法，精测时应用比例求解。对比实验证明，该编解码方法分辨率较高，测量更加准确，实现高精度、快速水准测量。测量范围为2-100 m，单点测量绝对误差小于±0.2 mm。

关键词：数字水准仪；精度；编解码；圆形编码；混合编码；面阵CCD

文献标志码：A 文章编号：1674-5124（2018）05-0017-07

0引言

测量仪器的数字化、智能化、小型化、多功能化是现代测绘技术发展的趋势。数字水准仪作为大地测量任务的一种基本而且重要的仪器，是集光、机、电、算为一体的高科技测量设备。目前，常用的数字水准仪在仪器构造和数据处理等方面存在一定的差异，但是其测量原理都具有共性。

当前数字水准仪在原理上有相关法、几何法和相位法3种自动电子读数方法。国产数字水准仪研究发展起步较晚，现有大部分技术均为单一形式的条形码进行编码。传统的数字水准仪在水准测量时，由于受视场的制约，近距离解码信息不足，远距离分辨率不高，所以精度受限。近几年来也不断有人提出新的使用二维编解码的方法。本文提出一种基于圆形为基本码元，多进制编码，并使用面阵CCD接收二维测量信号，同时使用了相关法和几何法的解码方法。

1数字水准仪编解码原理

1.1编码原理

仪器在测量范围（视距范围2～100 m，视线高0～3 m）上获得的任意一段图像与其他相同长度的图像互不相同。由于在2-100m的视距范围内，图像传感器接收的条码图像变化长达几十种，故对水准尺编码时要做到：

1）码元要足够大，使得仪器在远距离观测时，能够区分不同的码元。

2）码元的种类要足够多，在近距离测量时，最小码段图像有多重变化，使得仪器能够区分出标尺的不同位置。

视准测量时，主机和编码尺在空间上是分离的，而水准仪望远镜的视场角和焦距不变，于是存在以下问题：近距离时要满足一定的解码样本数，所以码元不能太大，中远距离测量时要使系统分辨率达标，码元又不能太小。实际上这是相互矛盾的：在仪器视场一定的条件下，码元如果越大，码元的种类就越少，就越难解决近视距时测量时的多值性问题：码元越小，远视距时就越难区分不同的码元。

本文提出的一种基于基本码元是圆形的标尺，远近不同距离采用不同进制编解码方案，解决传统条码尺近距离多值性问题和远距离距离分辨率低的问题。

图像测量中，标志点的选择直接关系到测量的速度和精度，在以往的标尺设计上，都是以条形码作为基本码元，在本方案中选用圆形码是考虑到：圆形码，形状规则，具有各向同性的优良性质，在图像处理过程中，圆心位置始终保持不变。

1.1.1多进制伪随机码

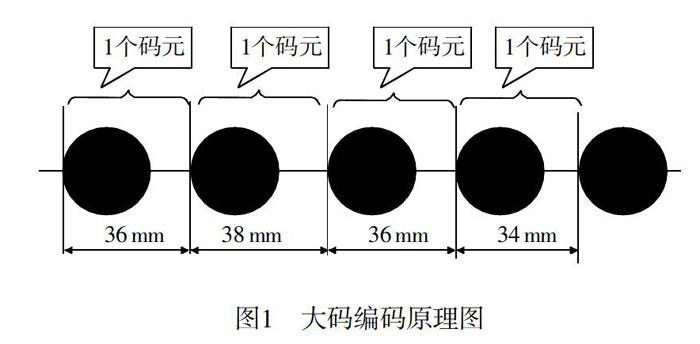
本文中所设计的编码方案，是一种非等距编码，同进制的圆的大小是相同的。以圆和圆心距作为基本码元，以图1大码为例，采用三进制编码，按着码元的长度也就是码元和码元之间的距离即圆心距进行编排，最小码段为4个码元，编码1对应圆心距为34mm，编码2对应为36mm，编码3对应为38mm。

以大码为中心，两侧对称分布有小码。小码采用四进制编码，每5个码元作为最小测量码段，4种小码，其圆心距分别为5，6，7，8mm，分别对应1，2，3，44种码元也按伪随机规律排列。小码的随机排列编制和大码的随机编制互不相关。标尺如图2所示。

1.1.2混合编码

在近距离物方视场较小，靶标视角较大的时候采用小码，使视场中有充分的解码信息，在远距离，物方视场较大，靶标视角较小，分辨率降低，则采用大码解码，使图像能够被分辨。

1.2解码原理

1.2.1图像预处理

面阵CCD采集到的原始图像数据，图像质量低，要对图像进行一些预处理，包括灰度化、图像增强、高斯平滑、中值滤波、自适应阈值以及去除环境噪声，得到方便图像识别和测量的信号，然后通过解码即可根据算法求出视高和视距，总体处理框图如图3所示。

边缘检测是影响数字水准仪测量精度的重要環节凹。图4、图5分别是测量时采集的原始图像和处理后的图像。

1.2.2视距的求解

如图6所示，对经过预处理后的图像进行行扫描，每行得到直线边缘间的像素数L_i，共扫描n（1000-1200）次左右，两条直线间的距离是已知的常量Width，那么综合CCD的焦距和像元尺寸，由图6所示的成像原理和式（1）得到视距，y为实际尺寸，y为在图像上所成像的尺寸。视距为

（1）

计算标尺两端刻线像素差L时，使用3σ方法剔除粗大误差可以减小误差，具体过程是：计算不同行的像素L_i，首先求平均值为

（2）

然后求出残差：

（3）

再求其标准差：

（4）

剔除3σ以外的粗大误差，再重新计算标尺的宽度，采用这种方法，可以避免标尺的微小倾斜导致宽度测量不准的问题。

像元尺寸δ为固定值4.5μm，在不同的视距像素分辨率为

（5）

视距：

（6）

1.2.3视高的求解

1）粗测

由以上可知，由于准确计算L，通过轮廓检测可以得到每个圆的外轮廓的位置，并且由灰度相关的质心定位法得到灰度圆的质心，然后由L同比可得圆的半径。

灰度相关的质心定位算法：

由式（5）算出的像素分辨率，能够计算出解码图像圆心之间的距离，再获得其对应的编码。比如在观测时，通过直线校准，获得观测距离为D，每两个圆心之间，根据图像处理后的结果计算圆心像素差，那么能获得这两个圆心的距离及圆心距对应的编码。

每连续的n个圆可以得到n-1个圆心距，那么就对应n-1个编码，超过4个就可以确定一个码段，由前面的伪随机码部分知，在用大码测量时4个及4个以上的编码才能在完整码上确定唯一位置。在图像解码过程中，无可避免地会存在着视距计算的偏差、图像边缘、噪声等的影响，解码也可能出现一定的偏差，导致出现错码的情况，那么就要使用最大相似匹配算法。

具体操作是，把解码得到的码段和完整的编码码段从起始位置开始的相同长度的一段码段进行比较。设置合适的权重，如果码值相同，字符串权值加K₁；码值差1，字符串权值加K₂；码值差2，字符串权值加K₃…，比较完所有字符串得到一个权值。再把解码得到的码段与完整码段第2位开始的码段进行比较，一直到比较结束。这样，通过一次完整比较，权值最大的位置所在的码段就是相似度最高码段，就确定了解码的码段在完整码中的位置，那么此时△H+△h在理论上就是一个确定值，如图7所示。视准轴高度

2）精测

在精测时，从视准轴中心分别向上和向下分别搜索一个码元，假设其距离上码元中心的距离是x，距离下码元中心的距离是y，由上面的粗侧部分可知两码元之间的距离z是已知的。

如图8所示，视准轴到下码元中心距离：

（10）

因为z是理论真值，由于图像处理中x和y会引入测量误差，经过图像处理后图像两边的膨胀或腐蚀效果相同，而△x是按着x和y的比例计算得到的，所以这种方法在理论上可以大大减少图像处理过程带来的误差。

视准轴到编码尺底端高度差：

H=△H+△h+△x （11）

2实验设计和数据分析

实验系统硬件包括，基于win7、64位操作系统的PC机，按照如上的编码规则制作的标尺，以及CCD相机。CCD相机型号是北京微视RS2300工业相机，象元尺寸4.5μm×4.5μm，焦距f=50 mm。

系统软件设计程序框图如9所示，为单次测量流程图。软件是通过Visual Studio 2013编写的基于对话框的MFC程序，软件界面如图10所示。图中显示了近距离解算时检测的圆心的位置。为进一步提高测量精度，取20次计算结果的平均值作为测量结果。

2.1实验结果

2.1.1圆形码元实验结果

由圆形码元制作的水准尺，分别模拟了在2.389，8.722，22.804，40.475，44.241，75.228，99.556 m远近不同的距离的实验，标尺固定在ABS光栅尺上，标尺每次在光栅尺上移动50 mm。所得的最近和最远的测量结果如表1和表2所示。

2.1.2条形码元实验结果

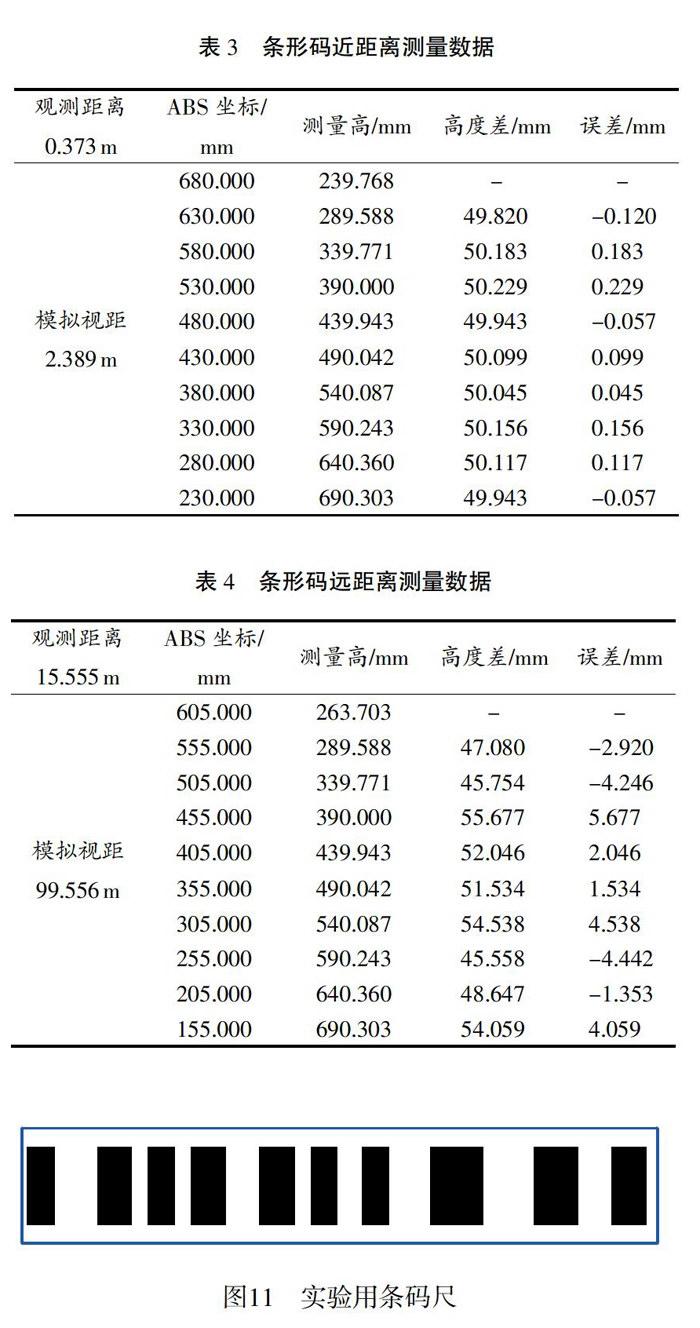
现有条码尺均有其对应的伪随机数列，由于这部分信息是不公开的，所以按照传统的条形码的设计方案，自制伪随机条形码进行解码。为了方便比较，设计条码宽度是42mm，最近视距在2m左右。四进制编码，条码尺如图11所示。在同样的环境中，模拟的最近和最远实验结果如表3和表4所示。

2.2数据分析

2.2.1圆形编码理论分析

由式（1）可以推导出视距和视场的关系。Height表示图像高度。

y=D/（f·δ·Height） （12）

设计2 m作为最近视距，10m左右作为远近视距的分界线，以大码观测为例，在视野内出现的码元数量为

那么与视距的关系理论计算结果如图12所示，从图中可以看出，在用圆形码小码观测时，在10m的时候测量误差最大，测量标准差是0.001mm，在用大码观测时在100 m时误差最大，测量标准差是0.014mm。

2.2.2条形编码理论分析

条形码的单点测量精度由式（5）可知：

单点测量精度与视距的关系如图13所示。从图中可以看出，在用条形码进行观测时，測量误差与观测距离成线性关系，在100m时，误差达到2.833mm。

2.2.3实验结果分析

通过实验测试远近不同距离下视高的观测精度，由表1～表4的观测记录可以看出，圆形码在最近和最远的高差测量标准差分别是+0.096mm，±0.143mm；同等测量环境条件下，条形码在最近和最远测量的高差标准差分别是±0.121 mm，±3.894mm。两种实验测量结果均比理论误差要大。误差来源主要包括CCD相机量化误差、标尺刻化误差、视准线误差、大气抖动，此外，光照不均匀等因素对图像的边缘提取也有一定的影响。在同等实验条件下，在近距离时，两种编码方式精度相近，但是当距离不断增加时，圆形编码的精度要高于条形码，在100 m左右的时候，圆形编码要优于条形码一个数量级。通过测试，软件进行一次测量的时间约为250ms。实验测试中，软件稳定、可靠。理论上观测距离能到100m，单点测量绝对误差小于0.2mm，符合常用的数字水准仪的测量精度要求。

3结束语

实验数据表明，本文所提出的编解码设计方案原理上是正确的，在技术上也是可行的，达到了准实时测量的要求。本文研究的成果为数字水准仪的研制奠定了一个良好的理论基础。同时，也给现有编码尺的设计方案提供了一种较好的设计思路，这种新型的设计方法，具有一定的实用价值。

（编辑：刘杨）