EWT—SVD在高速列车万向轴动不平衡检测中的应用
龙莹 苏燕辰 李艳萍 杨慧莹
摘要:万向轴是高速列车传动系统的核心部件,其动不平衡检测对保障列车运行安全具有重要意义。万向轴动不平衡特征主要体现在特征频率中,针对该信号的故障特征频率提取,引入经验小波变换(empirical wavelet transform,EWT)与奇异值分解(singular value decomposition,SVD)算法。该算法利用EWT构造一组小波滤波器组提取信号的固有模态分量,并通过Hilbea变换得到每个单分量信号的瞬时频率与瞬时幅值,使用SVD结合奇异熵增量谱确定重构阶数并对每个单信号进行重构消噪。通过构造一仿真信号对算法的有效性与可行性进行验证,并将该方法运用于万向轴动不平衡检测中,结果表明:该方法能准确地提取信号的特征频率,使得谱线分辨力得到提高,可有效地应用于万向轴动不平衡检测中。
关键词:信号分析;动不平衡检测;经验小波变换;奇异值分解;万向轴
文献标志码:A 文章编号:1674-5124(2018)05-0024-07
0引言
万向轴是CRH5型动车传动系统中的重要组成部分,它两端分别与牵引电机、齿轮箱通过十字万向节相连,主要起到传递动力的作用。万向轴结构细长,弯曲刚度和扭转刚度都很小,在运行时通常处于高速旋转状态,且需要适应复杂的运动关系。这样特殊的结构与工作性质使得其一旦出现动不平衡则极易产生极大的偏心力。偏心力的加剧会引起传动系统的振动加剧,轻则使影响传动部件的运作缩短使用寿命,重则导致轴承严重磨损,出现断轴等重大安全事故,因此,对万向轴进行动不平衡检测,保障列车传动系统正常运作显得尤为重要。
万向轴振动信号通常是非线性、非平稳信号。Wigner-Ville分布、短时傅里叶、小波分析、盲源分离等都常用与对于非平稳信号的分析与处理。Wigner-Ville分布中由于交叉干扰项的存在,限制了其对多分量信号的处理:短时傅里叶因存在窗函数的局限性,无法准确描述频率随时间的变换闭。近年来,经验模态分解(empirical mode decomposition,EMD)被广泛地应用于非线性、非平稳信号中,但其缺乏完备的理论基础,存在模态混叠、过包络、欠包络、端点效应等问题。针对EMD的不足,Gilles提出了经验小波变换(empirical wavelet transform,EWT)。该方法通过对信号的傅里叶谱进行划分,并构建一组正交小波滤波器组,对划分区域进行滤波提取固有模态分量。EWT十分适合处理非线性、非平稳信号,相较于EMD,它具有完备的理论基础,且能有效地提取固有模态分量,不存在虚假分量,计算量较之小,因此,在轴承、转子、齿轮箱的故障诊断中得到了成功的应用。
本文将EWT运用到高速列车万向轴动不平衡检测中,发现其能有效地提取万向轴故障特征信号,但是提取的特征信号谱线依旧杂乱,不易区分,因此为了使特征频率更加突出,本文运用了奇异值分解(singular value decomposition,SVD)方法来分解、重构提取出来的模态分量,并通过奇异熵增量谱确定重构阶次,提纯故障信号,提高谱线的分辨力。最后通过仿真信号来验证该方法的可靠性,并将其运用在万向轴动不平衡检测中。
1经验小波变换
1.1频带的划分
根据信号的重构公式,信号可以分解为固有的模态分量,如下式所示:
2奇异值分解及奇异熵增量
2.1奇异值分解理论
2.2奇异熵增量谱
3基于EWT-SVD的仿真信号处理
为了对算法的有效性进行验证,构造如下仿真信号:
仿真信號由5Hz正弦信号,基频为100Hz、调制频率为10Hz的调频信号,频率为214Hz的调幅信号与高斯白噪声组成。设定的采样时间为T=I s,采样频率为f=1000Hz,采样点数N=1000。该仿真信号的时域波形如图2所示。
将信号的频谱划分成3个频带,如图3所示,并构造3个滤波器分别提取信号分量。
根据频带的划分,EWT将仿真信号分解为3个信号分量C1、C2与c3,如图4所示。图中的3个分量信号明显存在着噪声干扰,因此将使用SVD方法结合奇异熵增量谱对分量信号进行消噪声。分别绘出3个分量的奇异熵增量谱,并显示前30阶,如图5所示。
从图中看出,C1从第3阶开始,奇异熵增量不再随着阶次的增加出现十分明显的下降,这代表着信号的有用信息已经逐渐达到饱和,因此选择前2阶的奇异值对信号进行重构。同理,对于C2与C3,分别选择前6阶与前2阶的奇异值对信号进行重构,3个分量信号重构后的时域波形如图6所示。与图4对比可知,各分量信号(特别是C3)噪声被消除,且出现较好的周期性。
图7为经过EWT-SVD处理后的希尔伯特变换时频图,在图中谱线清晰不杂乱,频率成分明显,噪声信号基本被滤除。由此可证明,EWT-SVD方法能够较好地提取信号分量与固有频率,且能够滤除噪声干扰,使得谱线明显,效果显著。
4万向轴动不平衡检测
为说明本算法能有效地提取故障特征频率检测万向轴的动不平衡,使用来自图8的试验台试验数据进行验证,该试验台的动力传递方式为:电机-齿轮箱-万向节-万向轴-万向节。
动不平衡轴选用了专项修轴,其动不平衡值大图9专修轴动不平衡实验数据于线路运用标准,测点为齿轮箱端最靠近万向轴的非旋转件上,万向轴的试验转速为2700r/min,采集的垂向加速度信号作为处理对象,采集的数据如图9所示。
若万向轴存在动不平衡则会出现周期性不平稳,且使其转频及倍频更丰富,因此选择万向轴的转频或倍频作为其动不平衡的故障特征频率,并通过提取万向轴的故障频率实现对万向轴动不平衡的检测。
该试验台中万向轴的转频为2 700/60=45 Hz,由于故障频率在傅里叶频谱的低频部分,因此对信号做300Hz低通滤波处理,再进行频带的划分,信号频谱如图10所示。虽然能够辨别万向轴频率,但是存在噪声和基础振动,分辨力较低。将信号的傅里叶谱划分为6个频带,将信号分解成6个分量,图11与图12分别为分量信号的时域波形图与频域波形图。
为了将EWT方法与EMD方法进行对比,下文也使用EMD方法对该试验信号进行处理,并给出分解结果如图13所示,与EWT方法相同,EMD也将试验信号分解成6个分量信号。分别绘出这6个分量信号的频谱图,如图14所示。
虽然EWT与EMD都将信号分解成了6个分量,但是通过对比图10、图12与图14可看出,EWT有效地将仿真信号的固有模态分量给提取出来,且不存在虚假分量:而在EMD的分解结果中存在模态混叠与虚假分量。通过观察对比可知,如图14中的C4与C5对应着图12中的C6,即本属于相同的成分的信息被分解成两份,且图14的C6中分解出原频谱(图10)不存在的虚假分量。通过对比两种方法可知,EWT比EMD能够更有效地分解出信号的固有模态分量,且具有相对完备的理论基础。因此,本文将在EWT的分解结果上进行后续的分析处理。
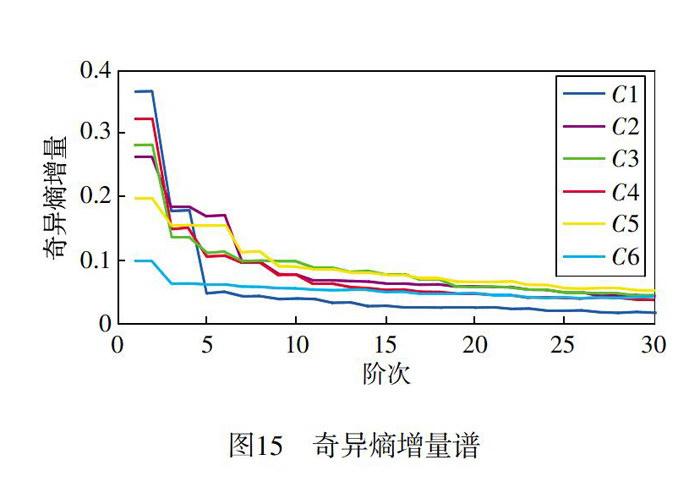
图15为EWT方法分解出的6个信号分量的前30阶奇异熵增量谱,根据奇异熵增量谱图,对于每一个信号分量,均选择前2阶奇异值对信号进行重构,重构后的信号分量如图16所示。
图17为EWT分解后信号的Hilbert变换时频图,图18为EWT-SVD分解后经过奇异值滤波之后的Hilbert变换时频图。由图17可知,频谱内聚集着5条频带,说明EWT很好地提取了信号的固有模态分量,但部分区域,谱线混杂。如图18所示,将各个分量经过奇异值分解重构之后,时频谱上出现6条十分清晰的谱线,分别是万向轴的转频及倍频,相比图17,万向轴的6倍频也清晰可见,该方法方法提纯了谱线,提高了谱线分辨力,使得谱线易于识别,一目了然。
通过使用EWTMSVD方法对万向轴试验信号的处理可知,该方法能有效地提取出万向轴的故障特征频率,且使得谱线清晰,特征更加明显,可实现对万向轴动不平衡的检测。
5结束语
本文介绍了基于经验小波变换与奇异熵增量谱的万向轴动不平衡检测的方法。经验小波变换对振动信号进行提取,在时域上将信号分解成一系列不同频率段的固有模态分量信号。针对信号分量受噪声干扰的情况,利用奇异值对信号进行分解,根据奇异熵增量谱来确定信号奇异值分解后重构的阶次,在确保信号有效信息完整的基础上提纯谱线,提高谱线的分辨力。仿真信号验证了该方法的有效性,该方法提取的固有模态分量与所包含的信号分量一致,没有虚假分量。且该方法在万向轴动不平衡检测中应用的结果表明,经验小波变换与奇异熵增量谱的联合算法能有效地提取万向轴的故障频率,且各個频率成分清晰明确,特征明显,为万向轴的动不平衡检测提供了一种新的手段。
(编辑:刘杨)