重力场模型研究进展及最新重力位模型精度比较分析

张 杰，孙 文，梅宇庭，范玉磊

(61243部队，新疆 乌鲁木齐 830006)

0 引 言

重力场模型是指用来表示地球重力位的一组已知系数，其核心是位系数值，现广泛应用于卫星发射、重力数据处理等多个领域[1]。在似大地水准面的逼近和求解中，重力位模型的精度能够很大程度影响似大地水准面计算精度，有必要对其进行详细比较与分析，以获取最佳模型和逼近阶数。

1 重力场模型研究进展

1.1 概述

构建重力场模型的方法主要有调和分析法和最小二乘配置法以及用于提高局部区域逼近精度的拼接法、谱权综合法等。目前，国内外学者和研究机构已发布多种系列、不同阶次的重力位模型。国外影响力较大的有美国俄亥俄州立大学的OSU系列，德国地学研究中心的EIGEN系列，美国国家地理空间情报局的EGM系列，美国德州大学奥斯汀分校空间研究中心的GGM系列等；国内主要有武汉大学的WDM系列，中科院测量与地球物理研究所的IGG系列，西安测绘研究所的DQM系列以及解放军测绘学院的UGM系列等[1]。

随着重力测量卫星(CHAMP、GRACE、GOCE)的发射，全球范围的时变重力场研究成为可能。相对固定的重力位系数模型、时变重力场模型除了提供传统的位系数之外还提供了与时间相关的变化参数，用于计算重力场随时间的变化。这是重力位模型理论研究的重大突破与跨越[1]。

1.2 研究进展

以下列出了一些具有代表性的模型及其详细情况(表1，时变重力场模型尚未有全球公认的优秀模型，故未予列出)。

表1中最具有代表性的为EGM系列，即EGM96和EGM2008[2]。EGM96联合卫星跟踪数据(包括LAGEOS、LAGEOS-2、Ajisai、Starlette、Stella和GFZ-1)、卫星测高数据(包括TOPEX/Poseidon、ERS-1和Geosat)以及地面重力观测数据求解得到360阶地球重力场模型和海面地形模型(Dynamic Ocean Topography Model)。EGM2008模型在EGM96模型的基础上增加了卫星跟踪卫星数据(GRACE)，使用经过进一步处理的卫星测高数据和地面重力数据构成全球5′×5′格网分辨率的重力异常模型；与地形相关的计算主要基于SRTM数据、南极和格陵兰岛的冰盖观测数据(ICESat激光测高数据)以及卫星测高构建的海深数据，这些数据形成一个全球地形模型DTM2006.0，然后通过DTM2006.0计算地形相关项。EGM2008模型相较EGM96模型不仅极大提高了空间分辨率(由30′×30′提高到5′×5′)，而且提高了各类扰动场元在全球范围内的逼近精度。例如EGM2008模型全球范围内逼近大地水准面的精度达到11.1 cm(共5个测试区域，不包括中国地区)，而在中国区域的逼近精度约为14 cm(移除系统差以后)。

表1 部分重力场模型概况

2012年德国地学中心发布了完整到1949阶次的全球重力场模型EIGEN-6C2[3]，相比EGM2008模型，前者增加了GOCE重力梯度观测数据，在高频信号方面具有较大提升，但有必要对其进行精度验证。自EGM2008模型发布以来，构建似大地水准面模型、重力场模型等所用参考模型一直为EGM2008，经过多年发展，EGM2008模型的高频信号部分已不能满足现实研究和工程需要。EIGEN-6C2利用了大量EGM2008所没有的GOCE卫星梯度数据，这将极大增加高频信号部分的模型精度。故本文选择将EGM2008模型与EIGEN-6C2模型进行比较分析。

2 重力场模型计算理论

2.1 扰动位的计算

利用重力位模型求解扰动位的公式如下：

(1)

2.2 勒让德函数及其导数计算

正常化伴随勒让德多项式的递推有多种方法，例如标准前向行推法、标准前向列推法、跨阶次递推法以及Belikov列推法等。吴星、王建强等[4-5]利用2160阶勒让德函数的递推计算详细比较了上述几种递推方法(表2)。

表2 4种递推方法的计算速度比较

前两种递推法在阶次较高时由于舍入误差迅速增大而精度有限[4]，后两种递推则不存在此问题；且Belikov列推法相对跨阶次递推法具有更高的计算效率，故本文选取Belikov列推法，其基本原理如下[3-4]：

(2)

利用重力位模型求解扰动场元的公式为：

(3)

其中，垂线偏差子午分量的计算涉及伴随勒让德多项式的导数计算[4]：

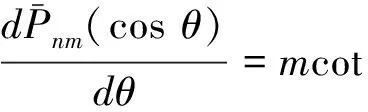
(4)

3 EGM2008与EIGEN-6C2模型比较分析

重力似大地水准面和重力垂线偏差的计算通常采用“移去—恢复”方法，即利用重力场模型精密逼近重力似大地水准面和重力垂线偏差的中低频部分信号，再利用移除模型重力异常的剩余重力异常数据计算其中高频部分，然后恢复全频段信号。

目前公认精度较高的全球重力场模型主要有2160阶次的EGM2008模型以及1949阶次的EIGEN-6C2模型，下面利用实测数据对两个超高阶重力场模型——我国的高程异常及垂线偏差逼近精度加以比较分析，计算时分别采用超高阶模型垂线偏差和重力异常单点计算公式，并考虑点位的高程数据。

3.1 垂线偏差精度

本文共使用我国境内1 381个实测GPS/天文点的数据进行模型垂线偏差精度比较(表3)。

垂线偏差子午分量与卯酉分量的计算误差变化情况如下所示(图1)。

表3 模型垂线偏差计算误差统计/″

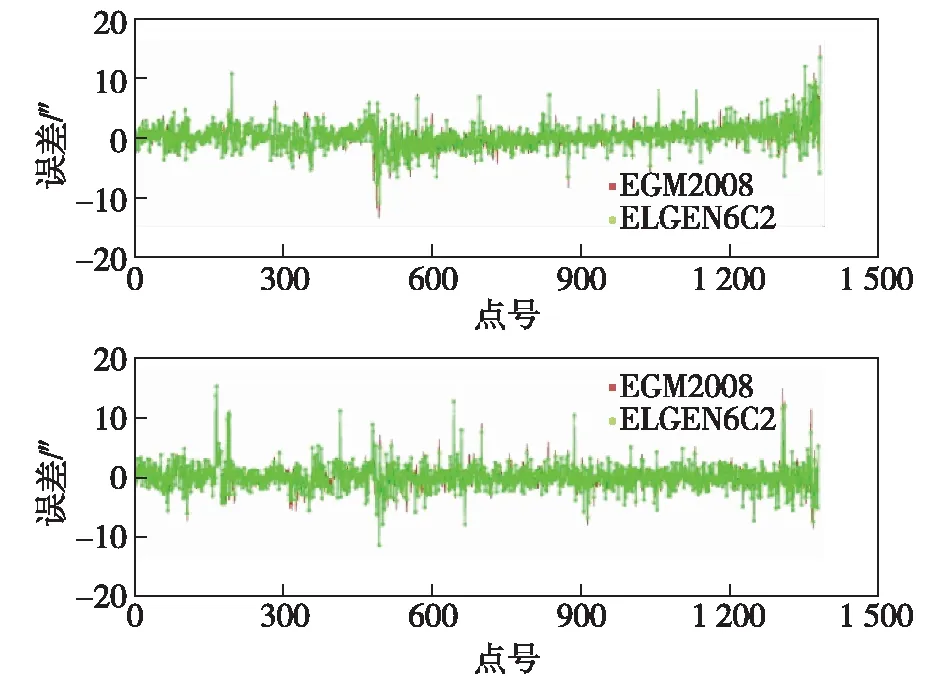
图1 模型垂线偏差误差变化

比较表3、图1可知，在垂线偏差的计算精度方面，两个模型在全国范围内的逼近精度较为接近，EIGEN-6C2模型精度略优于EGM2008。但比较两个分量的误差变化曲线可以发现，无论是子午还是卯酉分量，EGM2008的误差变化幅度较小，分析可能是因为实测数据较为陈旧，我国天文测量数据更新缓慢，这些点的实测垂线偏差存在较大误差造成的。

3.2 高程异常精度

本文使用我国境内各等级GPS/水准点共6 827个进行模型高程异常精度比较。以下列出了两种模型计算所得我国境内GPS/水准点的高程异常值与实测值比较的误差统计结果(表4)。

表4 模型高程异常计算误差统计/m

由表4可以看出，两种模型计算我国高程异常时均存在较大系统差，约为25 cm。分别统计两种模型在有系统差和无系统差情况下(减去各自误差均值)的计算精度，可以发现，无论从误差极值或均方根方面，EIGEN-6C2模型相比EGM2008模型都具有更高的高程异常计算精度，提高程度约为4 cm。

全国范围内GPS/水准点的模型高程异常计算误差如下所示(图2)，可以看出，EIGEN-6C2模型高程异常计算精度明显优于EGM2008模型。

图2 模型高程异常误差变化(有系统差)

4 结 语

由上述比较可以看出，相比EGM2008模型，无论是垂线偏差还是高程异常的计算，EIGEN-6C2模型的计算精度更高，更加适合作为我国大范围重力场逼近的参考场。同时，利用EIGEN-6C2模型结果与实测数据的对比，可以发现现有数据中可能存在较大误差的部分，从而需要进一步提升数据的使用效果，为今后实施复测提供一定参考。

[1] 刘晓刚. GOCE卫星测量恢复地球重力场模型的理论与方法[D].郑州：解放军信息工程大学，2011.

[2] Pavlis N K. An Earth Gravitational Model to Degree 2160: EGM2008[C]// EGU, General Assembly 2008, Vienna, 2008:13-14.

[3] 赵德军，张敏利，王强，等. EIGEN-6C2重力场模型在中国大陆的精度分析[J].大地测量与地球动力学，2014，34(5)：21-23.

[4] 吴星，刘雁雨.多种超高阶次缔合勒让德函数计算方法的比较[J].测绘科学技术学报，2006，23(3)：188-191.

[5] 王建强，赵国强，朱广彬.常用超高阶次缔合勒让德函数计算方法对比分析[J].大地测量与地球动力学，2009，29(2)：126-132.

[6] 海斯卡涅W A，莫里斯H. 物理大地测量学[M].北京：测绘出版社，1979.

[7] 陆仲连.地球重力场理论与方法[M].北京：解放军出版社，1996.

[8] 章传银，郭春喜，陈俊勇，等.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报，2009，38(4)：283-289.