南京市房地产价格时空变化研究

周 珺，季锴烨，马元辰，季皓聪

(南京师范大学地理科学学院，江苏 南京 210023)

0 引 言

改革开放以来，特别是1998年推行城镇住房制度改革以来，我国房地产事业高速发展，住房问题日益突出。房地产市场一直是大众关注的热点问题之一，且房产价格与人的生活、社会稳定息息相关。影响房价变动的因素多种多样、变化多端，这使得对房价的研究更加复杂。针对不同角度，很多学者都对房价进行了研究：如蒋芳等[1]基于GIS分析了北京市住宅地价空间分布规律；曹天邦等[2]研究了南京市主城区住宅地价的时空演变；曹瑞等[3]基于多项式回归对房价模型进行了分析等等。以上研究部分侧重于住宅地价空间分析，部分侧重于房价时空演变研究，还有部分侧重于房价模型分析。

近几年来，随着经济发展，南京房价也一步步攀升。为了研究南京市房地产价格时空变化，本文对南京市房价的空间分布规律进行了分析，探讨了空间上不同因素对房价的影响，揭示了房价在时间上的变化规律。

1 研究概况

1.1 研究范围以及数据来源

本文以整个南京市为研究区域(图1)，包括玄武区、秦淮区、六合区、鼓楼区、高淳区、江宁区、建邺区、溧水区、雨花台区、浦口区、栖霞区11个辖区。研究时间范围为2015年12月—2017年4月[4]。收集的数据为这17个月南京市二手房交易价格及其距周边最近医院、学校、商业中心等的距离[5-6]，数据收集来自各大房地产门户网站的二手房交易专区和百度地图。在对收集的数据进行一定筛选和整理后，最终保留了1 380个住宅小区数据。

图1 研究区域范围图

1.2 研究方法

在空间上，首先对房价数据进行统计分析；然后采用普通克里金插值方法对采样点进行空间插值，制作房价等值线；最后，在房价等值线基础上，选择一个中心基点，作房价剖面线，得到房价剖面图，从而对房价进行空间宏观分析。

在时间上，使用拉氏公式对不同时间段的房地产交易价格进行计算，得到月平均价格和房地产价格指数，使用合适的图表表达房价数据的大致变化趋势；通过研究南京各区的房价走势，将特殊变化的时间点与政策、活动等结合分析，探究影响其变化的因素。

在对房价产生基础认知后，在各种分析模型对比下，最终采用Hedonic价格模型[7]构建南京市房价空间分布模型。Hedonic价格模型主要是通过建立异质商品特征与价格之间的函数关系来估计每个属性所隐含的价格的，已被广泛应用于房地产价格研究领域。Hedonic价格模型有多种形式，包括线性模型、半对数模型和双对数模型等。

2 结果分析

2.1 空间分析

以2016年11月为例编制房价数据的统计直方图(图2)、正态QQPlot分布图(图3)、趋势分析图(图4)。

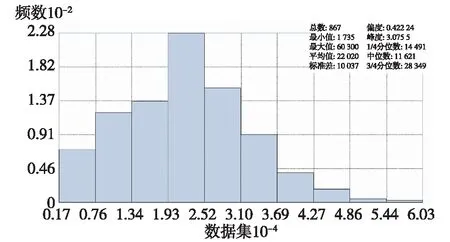
图2 统计直方图

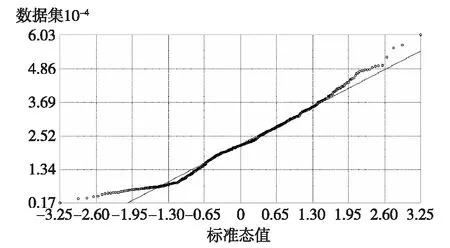
图3 正态QQPlot分布图

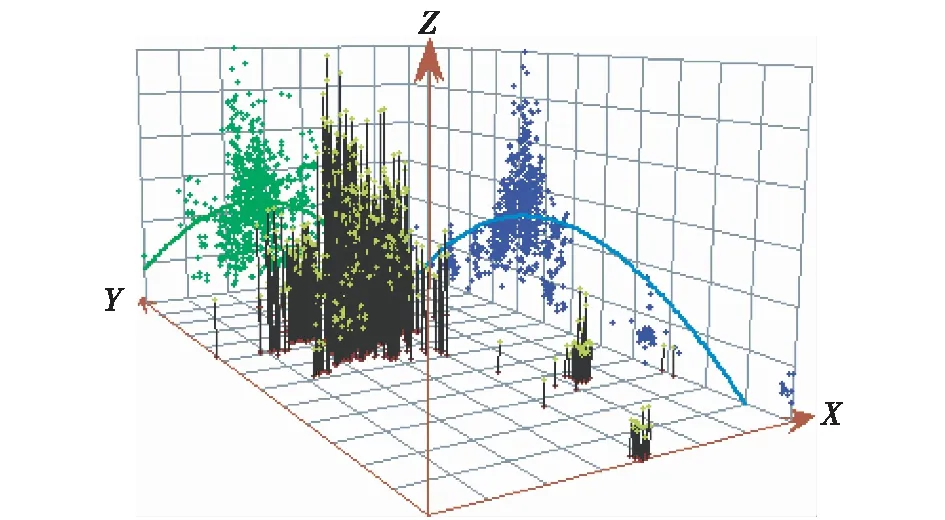
图4 趋势分析图

图2是利用2016年11月南京市房价原始数据生成的，从右上角的统计指标可以看出，直方图偏态为0.422 4。图3是南京市房价全局趋势分析，可以看出，各个方向都存在倒U形趋势。这表明，南京市房价具有在东西方向和南北方向上两边低、中间高的趋势，且通过图4可以看出，南京市的住宅小区均价在东北—西南方向与西北—东南方向也遵循两边低、中间高的趋势。通过对图2和图3的观察分析，可以得出2016年11月南京市房价数据近似符合正态分布。

空间插值是通过已知点的数据推求同一区域其他未知点数据的计算方法，主要包括趋势面法、不规则三角网法、距离倒数法和克里金插值法(Kriging)[8]。在对比之后，选择普通克里金插值法。

克里金插值首先考虑的是样点在空间位置上的变异分布，即确定对一个待插点值有影响的距离范围，然后用此范围内的样点来估计待插点的属性值。该方法在数学上可为研究对象提供一种最佳线性无偏估计(某点处的确定值)方法。它是在考虑待估计样点相互间空间位置等几何特征后，为达到线性、无偏和最小估计方差的估计，对每一个样点赋予一定系数，最后进行加权平均来估计的方法。

根据表3综合排序结果，综合指数值越大，水质越好。根据《地下水质量标准》中10种评价因子的界限值，由公式(6)得出其中5类水的综合指数值，Ⅰ类水界限指标排序为3；Ⅱ类水限指标排序为22；Ⅲ类水限指标排序为77；Ⅳ类水限指标排序为134；由于Ⅴ类水的界限指标为范围值，初始矩阵建立时，将其限值设为边界值，综合指数分值与Ⅳ类水一致，将<0.0018的综合指数值划分成Ⅴ类水，总体趋势是丘陵地区水质优于第四系覆盖区，内陆地区好于沿海地带,工业密集区上游好于下游地区，地下水质量评价分区见图3。

对2016年11月的房价数据进行普通克里金插值后得到房价分布图，在此基础上，绘制2 000元/m2的房价等值线结果(图5)。由图5可以看出，房价主要为圈层式结构：中心城区等值线密集且分布均匀，向四周等值线逐渐变得稀疏且分布不均。房价峰值区主要位于中心城区的新街口和五台山地区，由此向四周房价逐渐降低。除此之外，南京市房价的梯度变化在图5中也可以看出：由中心向四周的房价梯度变化较大，房价衰减较快；而城区外围房价梯度变化较小，房价衰减较慢。

整体看来，南京市房价在空间分布上具有连续性。在房价由中心向外降低的过程中，除部分地区存在突变情况外，整体上房价分布显示出连续特征。

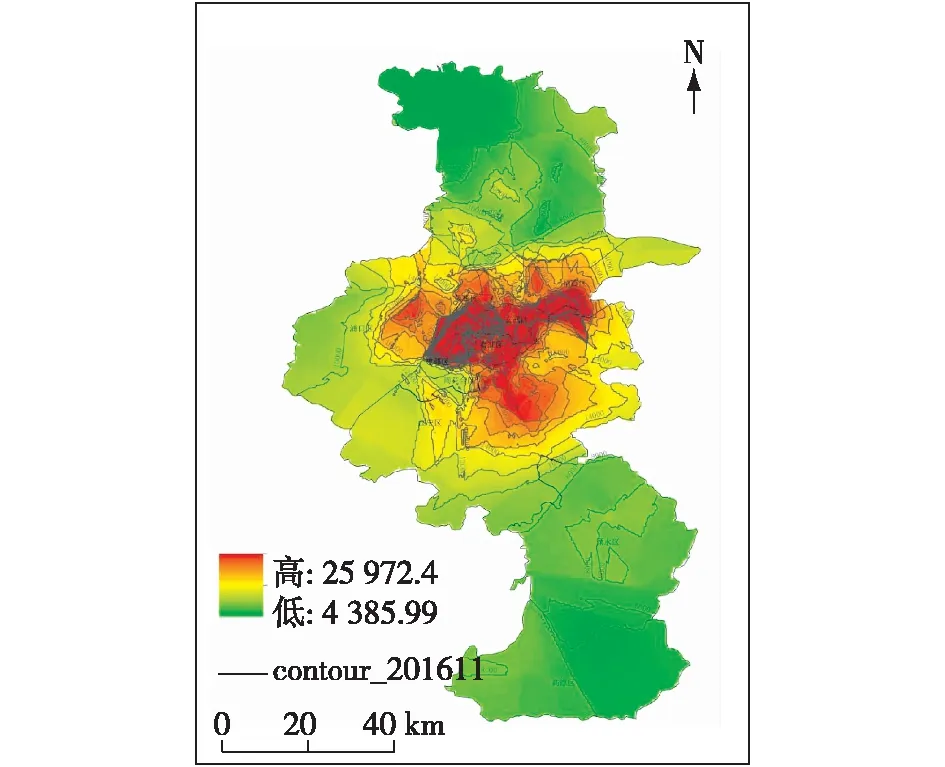
图5 2016年11月南京房价等值线图

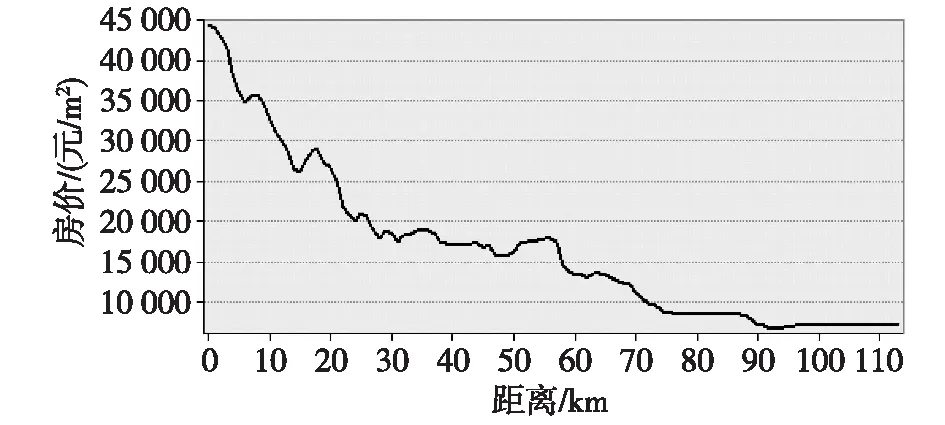
图6 房价剖面图(东北)

在2016年11月的房价等值线基础上，选取房价的最大值点为中线基点。由中心基点向东北、东南、西南、西北4个方向引剖面线，制作剖面图(图6—9)；做出过中心基点的东西向和南北向剖面线，制作剖面图(图10—11)。

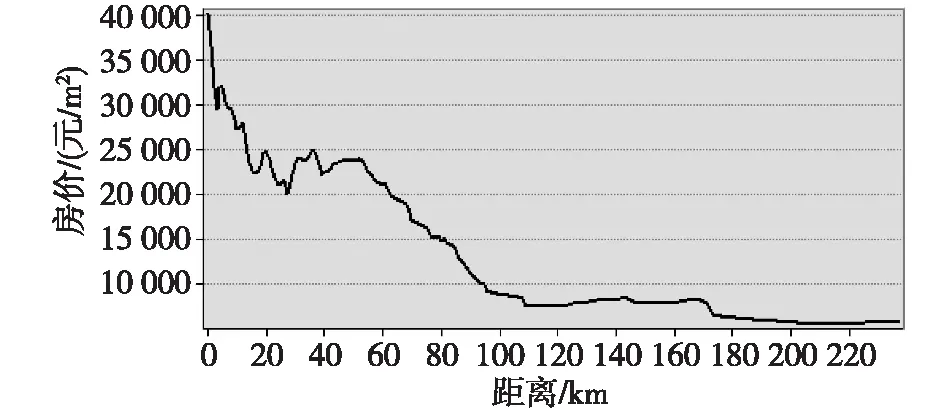
图7 房价剖面图(东南)

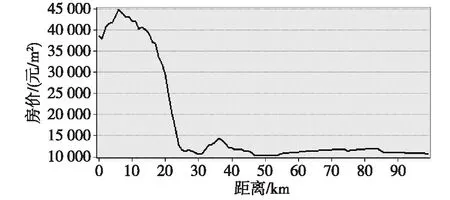
图8 房价剖面图(西南)

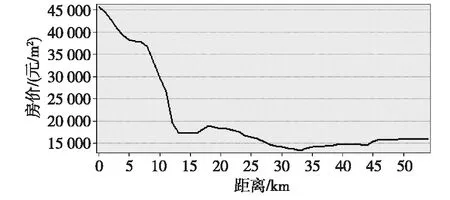
图9 房价剖面图(西北)

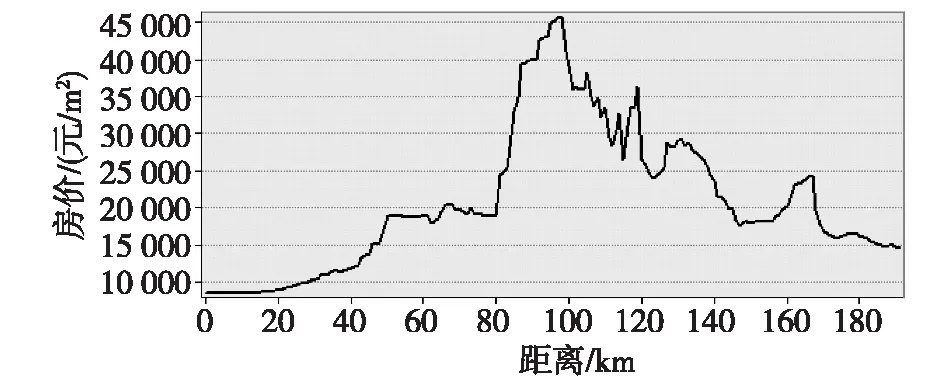
图10 房价剖面图(东西)

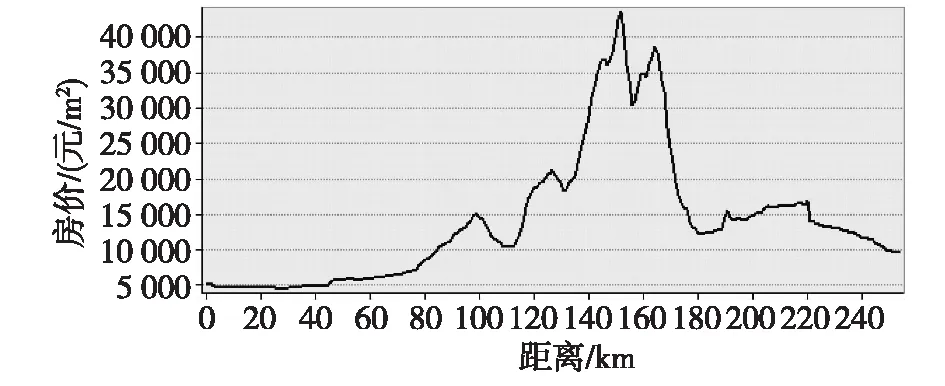
图11 房价剖面图(南北)

从图6—11可以看出，由中心基点到城区边缘的住宅用地价格在各方向上的递变具有不同特点，既有渐变又有突变，但总体呈逐渐下降趋势。

(1)图6呈现的是由中心基点向东北南京火车站、紫金山北麓方向延伸的房价变化趋势，房价在此沿线上呈现缓慢下降趋势。而在15 km左右出现的小峰值是因为靠近火车站以及紫金山北麓，区域交通便利，自然环境优美，人文积淀深厚。20 km左右出现的一个小峰值是因为区域位于仙林大学城，区域人文环境较高，房价随之升高。

(2)图7呈现的是由中心基点向东南方向延伸的房价变化趋势。可以看出，整体上，距中心基点越远，房价越低。而在20～30 km附近出现的房价峰值主要由历史原因及沿线地铁1号线通车导致的。

(3)图8呈现的是由中心基点向西南奥体中心方向延伸的房价变化趋势。可以看出，中心基点向西南方向的房价整体呈现下降趋势，其在距中心基点5 km左右达到峰值后出现一个下降陡坡，直至在20 km处形成阶地后房价趋于平缓。5 km处出现峰值的主要原因是南湖居住区的开发使得房价上升。

(4)图9呈现的是由中心基点向西北南京长江大桥方向延伸的房价变化趋势。从房价看来，房价变化趋势同西南方向相似。城北由于历史和城市发展战略方面原因，受瞩目程度不高，因此地价由中心至此下降较快。6 km左右由于临近狮子山，环境宜居，交通较为便利，故房价变化趋于平缓。

(5)由图10—11可以看出，从城区一个边缘到另一个边缘，房价整体呈先升再降的趋势。在图10中，由于奥体公园等建成，居住环境变好，住宅不断增多，使得房价剖面图在70 km左右出现一个小峰值，120 km左右的峰值是受紫金山风景区影响导致的。在图11中，140 km左右峰值出现的原因是位于市中心，基础设施完善、商业繁荣、交通便利，同时靠近玄武湖风景区，居住环境优美；170 km左右峰值出现的原因是位于月牙湖附近，自然环境好，房价较高。

2.2 时间分析

对2015年12月—2017年4月的南京市11个辖区房地产价格数据进行分析，通过拉氏公式计算得到整个南京市每月的平均房价[9]，使用房地产价格指数查看房价波动幅度及不同时期的房价涨跌情况(图12)。

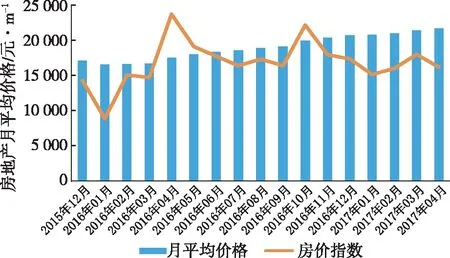
图12 南京市房地产月平均价格和房价指数

从图12可以看出，在不同时期，房价上涨情况不一致，如2016年1—4月时间段内，房价径直增长，最高增长率为5.27%，平均增长率为2.16%；在2016年5—9月期间，房价上涨情况有所缓和，增长幅度降低，平均增长率为1.49%；2016年10月—2016年12月，房价上涨幅度急剧增加，回归高值，最高增长率为4.41%，平均增长率为2.72%；在2017年2—4月时间段内，房价逐渐显现平稳增长趋势，平均增长率为1.36%。但是在2016年1月和2017年1月，这两年的第1个月，房地产价格下跌，但从趋势上看，下跌之后的房价迅速增长，房地产市场呈现迅速火爆的状态。

2016年2月，财政部降低二套房契税并对一定条件的住宅免征营业税，与此同时，南京市颁布的《进一步促进我市房地产市场健康发展的意见》表示坚决遏制捂盘惜售行为。大力放缓的政策导致房地产市场迅速回春，南京房价逐渐上涨，月平均价格迅速上涨至17 510元/m2。在房价增速过快的4月份，为平抑房价，南京发布楼市“限价令”，限制房价涨幅，有效减缓了房价的增长速度，房价增长率从5.27%降低至1.17%。2016年9月，南京重启“限购令”，宣布已有两套房的居民家庭不得构建新房，但限购政策不包括高淳、溧水和六合3区，体现了调控政策的差别化和精准化。2016年10月，房价增幅迅速升高至4.41%，为抑制房价激增，南京限贷和限购政策强化，加大了房地产市场的整顿力度，严格执行房地产贷款业务规制要求和调控政策。2016年11月又再次出台了新的调控措施，平缓房价增幅，稳定房地产市场。2017年上半年，南京深化房地产政策调控，完善限购政策，规范房地产市场秩序，房价增幅维持在1%—2%之间。南京政府出台的一系列房地产政策从延续2015年的宽松基调到大力收紧调控的政策力度，是紧紧围绕中央经济工作会议提出的“房子是用来住的，不是用来炒的”这一定位的。

3 建模分析

Hedonic价格模型有多种形式，包括线性模型、半对数模型和双对数模型。

(1)线性模型：

(1)

(2)半对数模型：

(2)

(3)双对数模型：

(3)

以2017年2月房价为例，首先根据已有房价和影响因素的空间位置信息计算距离每个小区最近的影响因素之间的距离。然后在R Studio中导入房价以及距离数据，再分别进行线性模型、半对数模型和双对数模型分析(表1)。

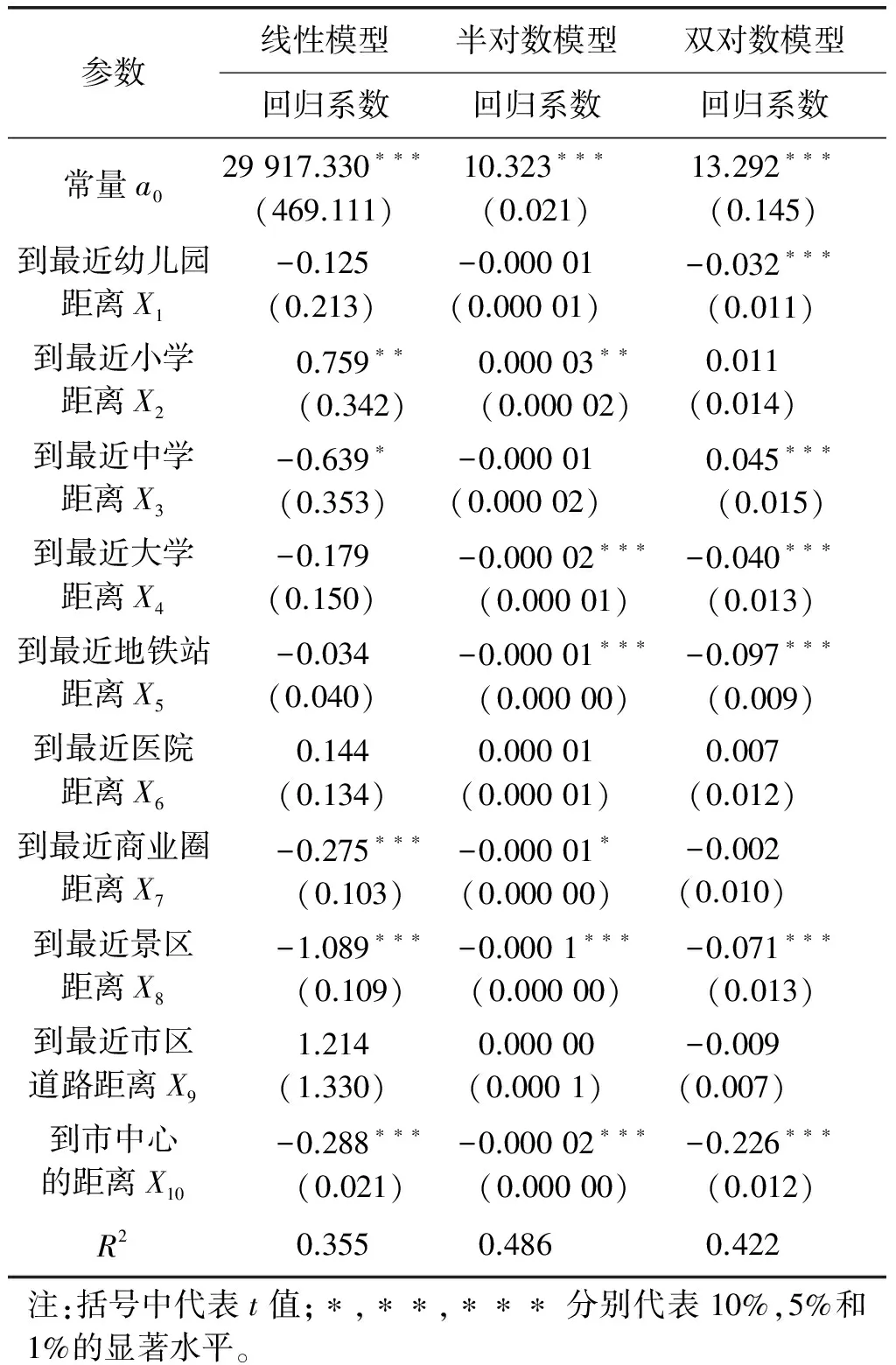
表1 Hedonic 3种模型回归系数表

比较表1所得结果发现，半对数模型的回归结果更加符合实际。该回归模型拟合优度为69.7%，R2=48.6%，表示所选取变量对市场房价至少有48.6%的解释能力。对半对数模型分析可知，幼儿园、中学、医院、市区道路的位置对房价影响不显著，所以减去这些因素再次建立模型，得到模型拟合优度为69.6%，R2=48.4%，这样可以用更少的要素更全面反映问题。

4 结 语

(1)从时间分析上来看，政策对南京房价的影响较大。大力放缓的房价政策能使南京房地产市场迅速回春，房价不断上涨。当房价涨幅高于一定水平时，颁布的政策能抑制房价激增，有效减缓房价增速。由此可见，房地产调控政策能规范房地产市场秩序，稳定房地产市场发展，对房价的影响较大。

(2)从空间分析上看，南京房价分布主要为圈层式结构，中心城区等值线密集且分布均匀，向四周等值线逐渐变得稀疏且分布不均。房价峰值区主要位于中心城区的新街口地区和五台山地区，由此向四周房价逐渐降低。由中心向四周的房价梯度变化较大，房价衰减较快；而城区外围的房价梯度变化较小，房价衰减较慢。可见，区位条件是影响住宅地价变化的主要因素：距市中心远近，中小学、高校、医院、景区和地铁的位置都对房价有影响[10]。

(3)总体分析，南京市房地产价格时空变化的研究有利于探索南京市房价变化的内在规律，构建的房价模型可以对房价进行预测，为民众购房提供参考。

[1] 蒋芳，朱道林.基于GIS的地价空间分布规律研究——以北京市住宅地价为例[J].经济地理，2005,25(2)：199-202.

[2] 曹天邦，黄克龙，李剑波，等.南京市主城区住宅地价的时空演变[J].地理研究，2012,31(6)：1029-1038.

[3] 曹瑞，周锋，欧阳广帅，等.基于多项式回归的房价模型分析[J].科协论坛：下半月刊，2010(12)：137-138.

[4] 陈珺.对时空数据管理中时间精度问题的讨论[J].现代测绘，2009,32(3)：12-14.

[5] 王彬.房地产价格影响因素分析[D].北京:北京交通大学,2007.

[6] 彭敏娟.长沙市商品房价格时空特征及其影响价格因素研究[D].长沙:湖南师范大学,2007.

[7] 王旭育.基于Hedonic模型的上海住宅特征价格研究[D].上海：同济大学,2006:1-107.

[8] 梅志雄，黎夏.基于ESDA和Kriging方法的东莞市住宅价格空间结构[J].经济地理,2008(5):862-866.

[9] 钟敏.广州市商品住宅价格时空变换研究[D].广州:广东工业大学，2012.

[10] 李志，周生路，张红富，等.基于GWR模型的南京市住宅地价影响因素及其边际价格作用研究[J].中国土地科学，2009,23(10)：20-25.