高速铁路接触网吊弦动应力数值模拟及其疲劳荷载特征分析

戚广枫 赵 慧 肖晓晖 徐鸿燕 李红梅

1.武汉大学动力与机械学院，武汉，430072

2.中铁第四勘察设计院集团有限公司，武汉，430072

0 引言

在高速电气化铁路中，机车通过其顶部的受电弓与接触线进行接触来获得电能。机车行驶工况下，受电弓沿着接触线高速运动会引起接触网的剧烈振动，长此以往会缩短其关键零部件的使用寿命。接触网主要由接触线、承力索、吊弦等组成，其中吊弦是接触线与承力索之间振动和力的传递者，也是高铁接触网最易发生疲劳断裂的零部件之一［1］。近五年来，京沪、武广高铁线路吊弦断股、断裂的问题持续发生，造成了严重的弓网故障，因此，研究吊弦的疲劳特性对保障高速铁路的安全运行有重要意义。

曹树森等［2］提出了基于神经网络的接触网结构抗风可靠性分析方法，为复杂的接触网结构动力可靠性分析提供了一条新途径。针对接触网吊弦的疲劳分析，德国力倍公司接触网零部件中心通过实验演示了吊弦在竖直方向的振动，但未对吊弦的疲劳特性进行更详细的分析。王伟等［3-4］对武广高速铁路接触网进行动态仿真分析，并根据吊弦疲劳试验要求的相关标准设计了一套吊弦疲劳试验台；LEE等［5-6］开发了一套吊弦疲劳试验机来分析吊弦的断裂方式，获得了吊弦的P-N疲劳曲线，并通过仿真分析研究接触线预弛度和车速对吊弦疲劳寿命的影响，得到了吊弦的疲劳寿命随着预弛度和车速的增大而缩短的结论。

综上，目前关于吊弦的研究主要集中在其疲劳原理分析、疲劳试验机开发等方面，未形成用于指导疲劳试验和寿命预测的疲劳载荷谱。由于目前国内高铁多采用双弓运行方式，因此本文考虑双弓运行工况，对高铁接触网系统进行动力学仿真分析，编制吊弦的疲劳载荷谱，为吊弦的寿命预测和疲劳试验提供依据。

1 弓网动态仿真方法

1.1 弹链型接触网模型

弹链型接触网主要由承力索、接触线、弹性吊索、吊弦、支撑杆、定位器等组成。根据接触网各结构件的受力特点，对其进行简化，并建立接触网的有限元模型［7-8］。图1所示为弹链型接触网单跨模型。其中，接触线、承力索和弹性吊索采用梁单元进行模拟；吊弦线密度较小，采用弹簧质量单元，其质量平均分配到吊弦两端的承力索和接触线；支撑杆采用弹簧质量单元进行模拟，其一端为固定约束，另一端等效为质量单元附加于承力索上，两端之间用弹簧单元连接；定位器用质量单元模拟，作用在接触线相应位置处。本文采用的接触网参数见表1，建立13跨接触网模型进行研究。

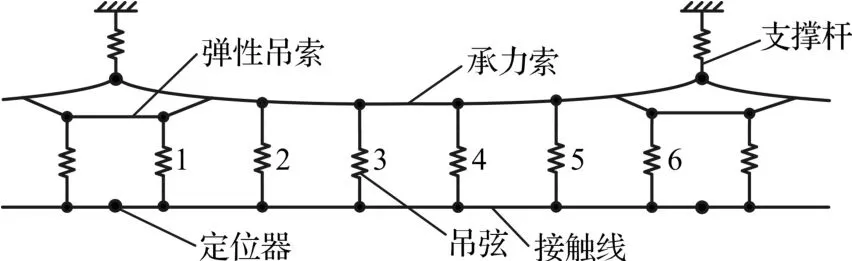
图1 弹链型接触网单跨模型Fig.1 Stitched catenary with one span

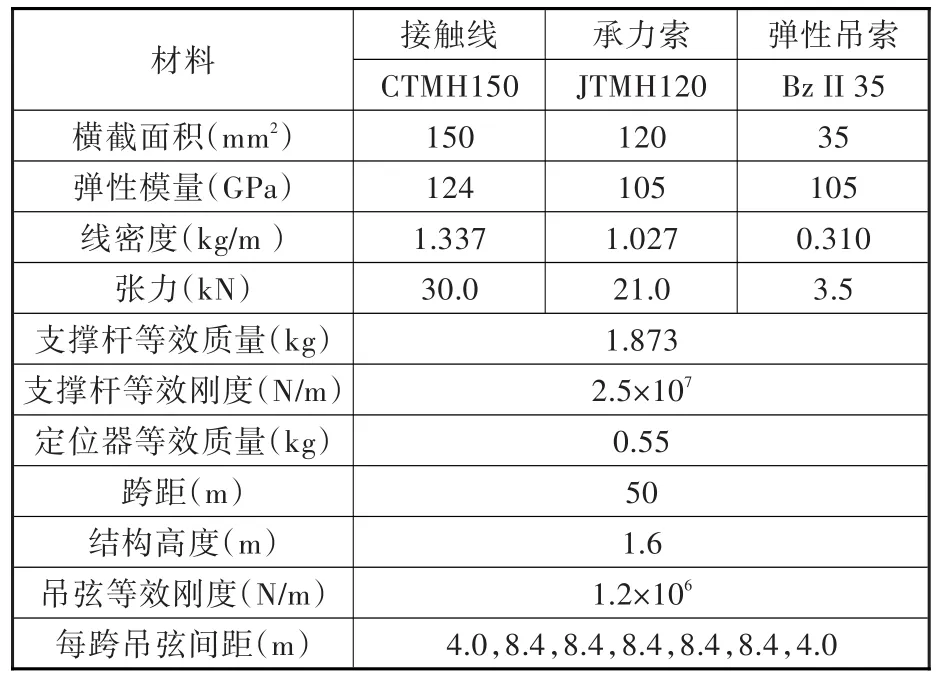
表1 接触网参数Tab.1 Parameters of the catenary

1.2 受电弓模型

受电弓主要由弓头、框架、底架和传动机构组成，本文采用三质量-弹簧-阻尼系统［9-10］模拟用于弓网仿真的受电弓模型。不考虑机车的振动，把受电弓的基座视为固定不动，图2所示为受电弓的三质量简化模型，其相关参数见表2。图2中，m1、k1、c1、y1分别为接触滑板和弓头可动的支撑部件的质量、刚度、阻尼和位移；m2、k2、c2、y2分别为固定的弓头部件和上框架的质量、刚度、阻尼和位移；m3、k3、c3、y3分别为上框架除归算至质量块m2以外及其他部件的质量、刚度、阻尼和位移；F0为受电弓的静态升弓力。

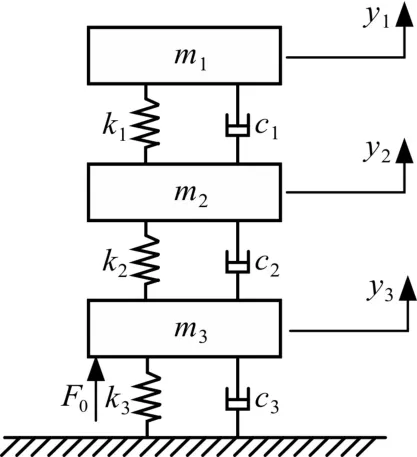
图2 受电弓三质量简化模型Fig.2 Three-mass simple model of the pantograph

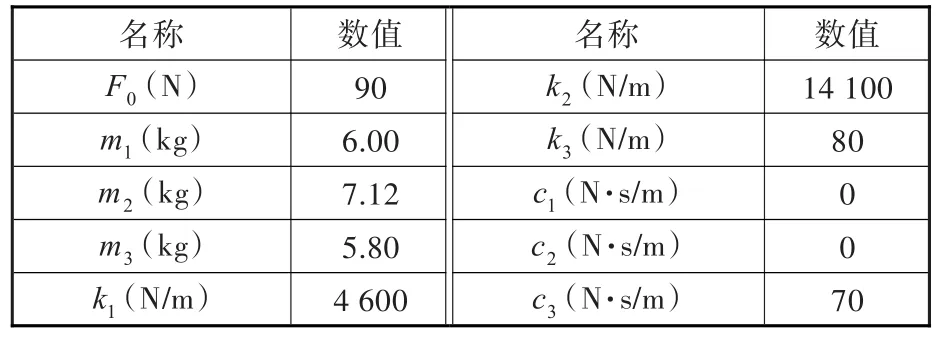
表2 受电弓结构参数Tab.2 Structure parameters of the pantograph

1.3 弓网系统动态仿真计算

根据上述建模方法，在ANSYS软件中建立接触网和受电弓的有限元模型。承力索、弹性吊索和接触线采用BEAM3二维梁单元进行模拟；吊弦、支撑杆采用COMBIN14单元进行模拟；定位器、线夹等具有集中质量属性的结构均简化为MASS21单元。考虑接触网结构整体的重力作用，施加承力索、弹性吊索、接触线预拉力，对接触网系统进行静态找形，从而确定接触网的初始形态，完成吊弦的长度计算［11-12］。

受电弓与接触网之间存在动态接触力P(t)，属于接触耦合，该动态接触力是时间的函数，可根据文献［13］中的研究方法进行计算：

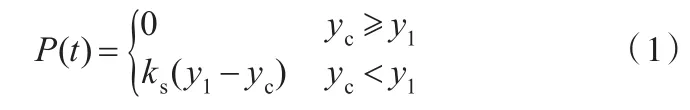
式中，yc为弓网接触处接触线的垂向位移；y1为弓头等效部分的垂向位移；ks为接触刚度，其值为82 300 N/m。

综上，可得到弓网耦合系统动力学平衡方程：

式中，M、C、K分别为结构质量矩阵、阻尼矩阵和刚度矩阵；U、U˙、U¨分别为结构节点位移向量、节点速度向量和节点加速度向量；F为结构节点载荷向量。

本文采用ANSYS平台进行该弓网耦合模型的动力学仿真计算，提取接触网系统仿真环境下各跨吊弦的力时程。

2 疲劳载荷谱编制方法

为编制吊弦的疲劳载荷谱，本文首先采用雨流计数法对跨段中各个吊弦的应力时程进行分级统计计数，从而得到其应力统计谱；再用Goodman直线方法对应力载荷谱进行零均值应力转换得到块状的疲劳载荷谱。具体过程如图3所示，分析步骤如下：①在ANSYS软件中编写APDL程序实现弓网系统的建模和动态仿真计算，提取吊弦各个单元的应力时程。②对吊弦各个单元的应力时程进行雨流计数，得到分析单元的各级应力幅值、应力均值和应力循环次数。③根据Goodman直线对雨流计数得到的应力统计谱进行零均值应力转换，从而获得用于指导试验和预测疲劳寿命的块状疲劳载荷谱。

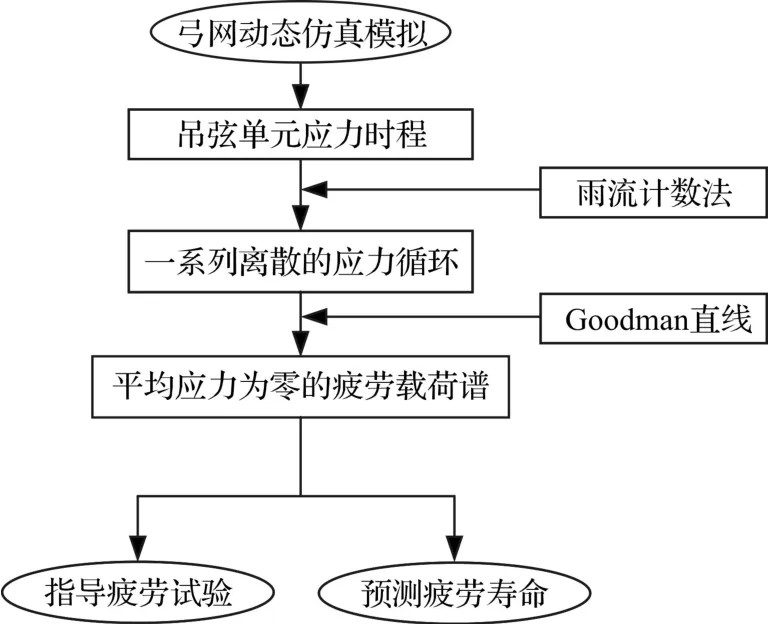
图3 载荷谱编制原理图Fig.3 Schematic diagram of fatigue load spectrum compilation

2.1 雨流计数法

根据弓网耦合系统动态仿真得到的应力时程是随机载荷，必须用计数法将随机载荷等效转化为变幅或恒幅载荷谱，才可用于疲劳寿命估算，进而指导疲劳试验。雨流计数法是基于材料应力-应变行为而提出的一种计数方法（属于双参数计数法的一种［14］），能将载荷谱以离散载荷循环的形式表示出来，计数结果用应力幅值、应力均值和应力循环次数来表示。

2.2 Goodman直线

雨流计数统计得到的是随机动载荷的应力均值和应力幅值二元随机变量的联合分布矩阵。为简化编谱过程，同时考虑平均应力对疲劳性能的影响，本文采用Goodman直线［15］将变幅疲劳应力修正为平均应力为零（即应力比为-1）的疲劳载荷谱，实现当量二维应力谱的一元化。Goodman直线表达式为

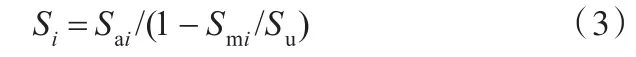
式中，Si为第i级应力循环的等效零均值应力；Sai为第i级应力循环的幅值；Smi为第i级应力循环的均值；Su为材料的强度极限。

3 结果与分析

3.1 吊弦的动态力分析

根据国内现行高铁的行驶工况，确定6种仿真工况，即双弓运行模式下250 km/h、280 km/h、300 km/h、310 km/h、330 km/h、350 km/h六种时速的工况。为了方便描述，以下将双弓运行工况简写为字母D。提取接触网系统仿真环境下第三跨各个吊弦的力时程，其中D300 km/h工况下的仿真分析结果如图4所示。由图4可以看出，初始状态下吊弦受初始拉力（即轴向力）作用处于拉伸状态。在列车前后弓依次通过时，吊弦下端向上抬起产生一定的压缩量，但其轴向力始终不小于零（即吊弦始终处于拉伸或松弛状态），这与吊弦在实际运营下的状态一致。中间位置的吊弦（2、3、4、5）与靠近定位器处的吊弦（1、6）相比，其初始拉力更大，受电弓经过时的动态力更大，振动也更加剧烈。

表3所示为D250 km/h和D300 km/h工况下的静态力和最大吊弦力，其中静态力是指列车经过各个吊弦前其轴向力的平均值。由表3可知：中间位置吊弦（2、3、4、5）的静态力约为靠近定位器处吊弦（1、6）的静态力的1.4倍；车速为250 km/h时，吊弦的最大吊弦力是其静态力的1.3～1.6倍，而车速为300 km/h时，吊弦的最大吊弦力是其静态力的1.3～2.6倍；D300 km/h工况下吊弦振动时的最大吊弦力是D250 km/h工况下最大吊弦力的1.1～2.0倍。

图4 D300 km/h工况下吊弦的力时程曲线Fig.4 Force histories of the droppers under D300 km/h

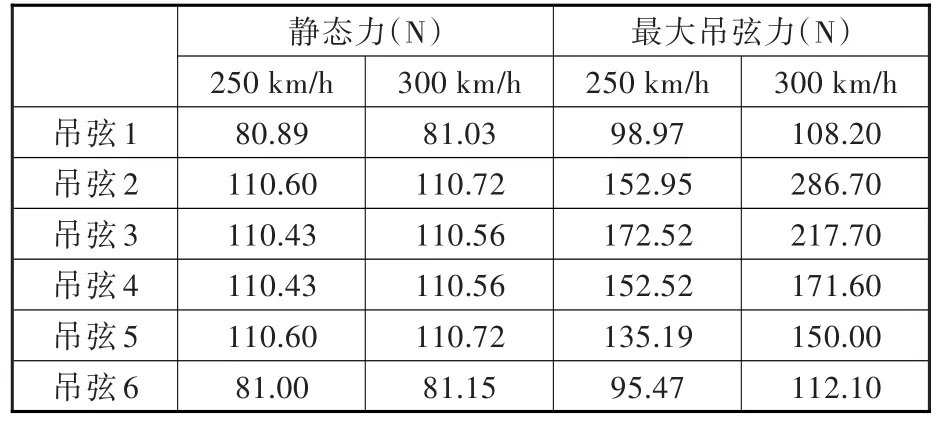
表3 D250 km/h和D300 km/h工况下的静态力及最大吊弦力Tab.3 Static force and maximum force of the droppers under 250 km/h and 300 km/h working condition

3.2 载荷计数

结合列车行驶工况下吊弦力时程曲线的幅值和均值，吊弦的载荷级数采用32级。根据表4所示的吊弦线结构参数，将力时程数据转化为等效应力时程数据并进行雨流计数，可得到不同工况下各吊弦的应力统计谱和雨流计数统计直方图。限于篇幅，本文仅给出D300 km/h工况下跨中左侧吊弦的雨流计数统计直方图，如图5所示。

表4 吊弦线的结构参数Tab.4 Structure parameters of the dropper

3.3 载荷谱编制

采用等寿命关系转化法，基于上述Goodman直线方法得到吊弦的零均值载荷。在各个吊弦的疲劳载荷谱编制过程中，剔除了计数统计后各工况下应力循环次数为零的组合。限于篇幅，本文仅给出吊弦1的疲劳载荷谱，如表5所示。

对D300 km/h工况下的吊弦载荷谱进行分级统计，可得到吊弦载荷谱分析图（图6）。由图6可以看出，靠近定位器的吊弦（吊弦1、6）的最大应力循环值为8 MPa，且出现该应力值的频次为1；中间位置吊弦（吊弦2、3、4、5）的载荷谱向高应力区扩展，吊弦2、5的最大应力循环值为17 MPa，最大应力循环值19 MPa出现在吊弦3、4处。整体而言，在同一行驶车速下，靠近定位器的吊弦（吊弦1、6）较中间位置吊弦，其低应力出现的次数多，高应力出现的次数少，因此在其载荷谱中，含有的低应力循环成分多，相应的高应力循环成分少，且吊弦安装位置越接近跨中，高应力循环次数越多，因此安装在跨中附近的吊弦（吊弦3、4）最易发生疲劳破坏。对跨中附近的吊弦3、4进行分析，可得到不同车速下的疲劳载荷谱分析图（图7）。

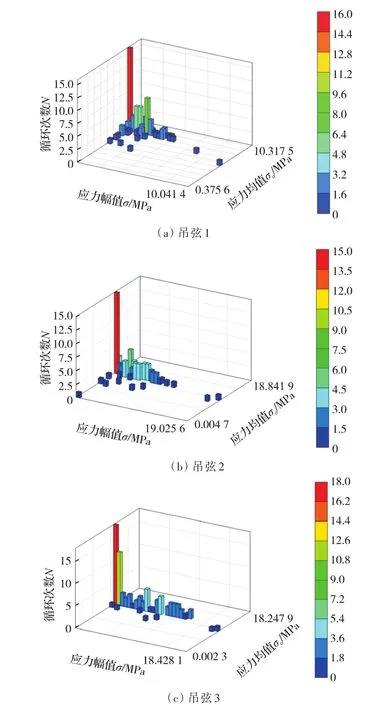
图5 工况D300 km/h下，跨中左侧吊弦的雨流计数统计直方图Fig.5 The histogram using rain-flow counting method for midspan droppers under 300 km/h working condition

图7a为不同车速下吊弦3的载荷谱分析图，可以看出，随着行驶速度的增大，低应力的循环次数不断减少，而高应力循环次数不断增多：当列车行驶速度为250 km/h时，1 MPa的低应力循环次数为57，10 MPa为该速度下的最大应力循环值；当速度增大到350 km/h时，1 MPa的低应力循环次数减少到20，约为250 km/h时低应力循环次数的三分之一，而最大应力循环值增大到了22 MPa，其数值为250 km/h时最大应力循环值的2.2倍。

图7b为不同车速下吊弦4的载荷谱分析图，可以看出，其随车速的变化规律与吊弦3基本相同，但车速高于300 km/h时，吊弦3相对于吊弦4更容易发生疲劳断裂：车速为310 km/h、330 km/h、350 km/h时，吊弦4的最大应力循环值分别为17 MPa、17 MPa、19MPa，比同等条件下吊弦 3的最大应力循环值小5%、5%、20%。

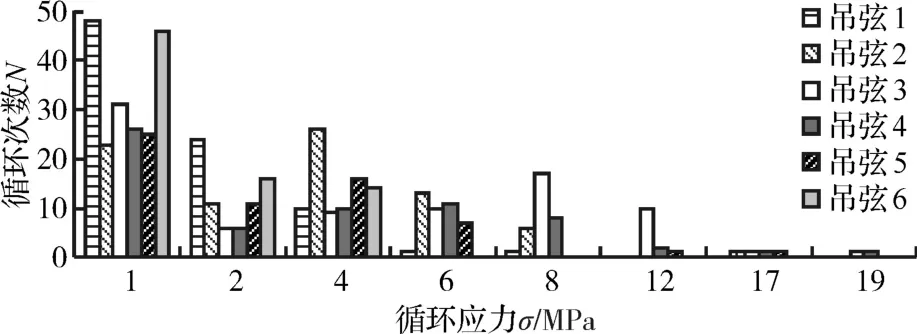
图6 D300 km/h工况下，吊弦载荷谱分析图Fig.6 Analytical diagram of fatigue load spectrum of droppers under D300 km/h working condition

图7 不同车速下，跨中吊弦的载荷谱分析图Fig.7 Analytical diagram of fatigue load spectrum of midspan droppers under different running speeds

4 结论

（1）中间位置吊弦静态力约为靠近定位器处吊弦静态力的1.4倍，双弓300 km/h工况下吊弦振动时的最大吊弦力最大可达双弓250 km/h工况下最大吊弦力的2倍。

（2）在同一车速下，吊弦安装位置越靠近跨中，高应力循环次数越多；靠近定位器的吊弦，低应力循环次数比跨中吊弦的低应力循环次数多。

（3）对跨中附近的吊弦而言，随着车速的增大，吊弦的载荷谱向高应力区扩展。当列车以高于300 km/h的速度行驶时，沿行车方向先经过的吊弦更易发生疲劳断裂。

参考文献：

［1］ 戚广枫.高速铁路接触网安全可靠性及可维修性研究［M］.成都：西南交通大学出版社，2012：47-52.

QI Guangfeng.Reliability and Maintainability of Highspeed Railway Catenary［M］.Chengdu：Southwest Jiao⁃tong University Press，2012：47-52.

［2］ 曹树森，柯坚，刘晓红，等.风荷载作用下接触网结构动力可靠性分析［J］.中国机械工程，2011，22（9）：1018-1021.

CAO Shusen，KE Jian，LIU Xiaohong，et al.Dynamic Reliability Analysis of Catenary under Wind Load［J］.China Mechanical Engineering，2011，22（9）：1018-1021.

［3］ 王伟，吴积钦，关金发，等.高速铁路接触网疲劳试验台［J］.高速铁路技术，2014，5（3）：22-25.

WANG Wei，WU Jiqin，GUAN Jinfa，et al.A Fatigue Test Rig of High-speed Railway Catenary Dropper［J］.High Speed Railway Technology，2014，5（3）：22-25.

［4］ 王伟.高铁接触网吊弦疲劳特性研究［D］.成都：西南交通大学，2014：1-5.

WANG Wei.Fatigue Characteristics Analysis of Cate⁃nary Droppers in High-speed Railway［D］.Chengdu：Southwest Jiaotong University，2014：1-5.

［5］ LEE K，CHO Y H，PARK Y，et al.A Study on Assess⁃ment of Dropper Life for Conventional Line Speed-up［C］//Proceedings of the 9th World Congress on Rail⁃way Research.Uiwang-city，Korea，2011.

［6］ LEE K，CHO Y H，PARK Y，et al.Improvement of Ex⁃

isting Overhead Lines for 180 km/h Operation of the Tilting Train［C］//Proceedings of the 8th World Con⁃gress on Railway Research.Uiwang-city，Korea，2008.

［7］ ZHANG Weihua，LIU Yi，MEI Guiming.Evaluation of the Coupled Dynamical Response of a Pantograph-cate⁃nary System：Contact Force and Stresses［J］.Vehicle System Dynamics，2006，44（8）：645-658.

［8］ ZHANG Weihua，ZHOU Ning，LI Ruiping，et al.Panto⁃graph and Catenary System with Double Pantographs for High-speed Trains at 350 km/h or Higher［J］.Jour⁃nal of Modern Transportation，2011，19：7-11.

［9］ BAUTISTA A，MONTESINOS J，PINTADO P.Dynam⁃ic Interaction between Pantograph and Rigid Overhead Lines Using a Coupled FEM-multibody Procedure［J］.Mechanism and Machine Theory，2016，97：100-111.

［10］ 阮杰.电气化高速铁路接触网与受电弓动态性能研究［D］.武汉：武汉理工大学，2013：42-44.RUAN Jie.Study on the Dynamic Performance of Overhead Contact System and Pantograph for High Speed Railway［D］.Wuhan：Wuhan University of Technology，2013：42-44.

［11］ CHO Y H.Numerical Simulation of the Dynamic Re⁃sponses of Railway Overhead Contact Lines to a Mov⁃ing Pantograph，Considering a Nonlinear Dropper［J］.Journal of Sound and Vibration，2008，315（3）：433-454.

［12］ LEE J H，PARK T W，OH H K，et al.Analysis of Dy⁃namic Interaction between Catenary and Pantograph with Experimental Verification and Performance Eval⁃uation in New High-speed Line［J］.Vehicle System Dynamics，2015，53（8）：1117-1134.

［13］ ZHOU Ning，ZHANG Weihua.Investigation on Dy⁃namic Performance and Parameter Optimization of Pantograph and Catenary System［J］.Finite Elements in Analysis and Design，2011，47（3）：288-295.

［14］ KHOSROVANEH A K，DOWLING N E.Fatigue Loading History Reconstruction Based on the Rain⁃flow Technique［J］.International Journal of Fatigue，1990，12（2）：99-106.

［15］ 陈传尧.疲劳与断裂［M］.武汉：华中科技大学出版社，2002：3-33.CHEN Chuanyao.Fatigue and Fracture［M］.Wuhan：HuazhongUniversityofScienceand Technology Press，2002：3-33.

（编辑 胡佳慧）

作者简介：戚广枫，男，1964年生，博士研究生。研究方向为高铁接触网工程。获国家科技进步二等奖1项。出版专著3部，发表论文16篇。E-mail：qiguangfeng@126.com。肖晓晖（通信作者），女，1969年生，教授、博士研究生导师。研究方向为复杂机电系统动力学分析与控制、机器人学。获国家科技进步二等奖1项。发表论文60余篇。E-mail：xhxiao@whu.edu.cn。