载波相偏估计算法研究

金慧琴，王正磊，朱安周

（1海军航空工程学院电子信息工程系，山东烟台264001；2.91697部队山东青岛266000）

根据实现结构的不同，载波同步算法有两种实现方式：闭环结构和开环结构[1]。闭环结构精度高，实现简单，但收敛慢；开环结构虽然实现复杂，但其捕获时间短。本文主要考虑基于开环结构的载波同步算法。载波同步包括载波频率同步和相位同步两部分[2]，分别通过载波频偏估计和校正、载波相偏估计和校正实现同频和同相。短波信道属于频率选择性衰落信道，关于此类衰落信道条件下的频偏估计的研究很少，大部分研究都是针对高斯白噪声信道的。这些研究的前提是，经过均衡的信号已经去除了码间干扰，使得均衡后的信号近似符合高斯白噪声条件[3]，此前提成立的条件是均衡算法不受频偏的影响。否则，由于频偏的影响，均衡效果很差，本文在研究载波相偏估计算法基础上，给出改进的载波相偏估计算法。

1 载波相偏估计算法

利用载波频偏估计算法估计出频偏后，对接收信号进行频偏补偿，以消除频偏的影响：

由于频偏估计算法本身具有一定的误差，使得估计频偏与实际频偏存在一定的误差，称为剩余频偏[4]，它会产生一定的相位误差；同时，发送端与接收端之间的不同步使得接收信号本身存在相位误差，基于以上两个原因经过频偏校正后的信号，会存在相位旋转，需要载波相偏估计与校正技术来消除相位误差的影响。

1.1 最大似然估计

进入载波相偏估计器之前，假定已经完成定时同步、频偏估计及校正。将总通信时间分成若干个短时间段，在每个短时间段内，剩余频偏相对于符号速率已经非常小，由它引起的相位变化非常缓慢[5]，此时载波相位可表示为：

其中表示第i个时间段内的平均相位，n(k)为噪声，此时可以认为在短时间段内不存在剩余频偏，只有相偏。信号模型表示如下：

其中sk是发送符号，φ是需要估计的载波相偏；wk是均值为零、方差为2σ2的高斯白噪声，实部和虚部相互独立；N为观察数据长度。观察数据的联合概率密度函数为：

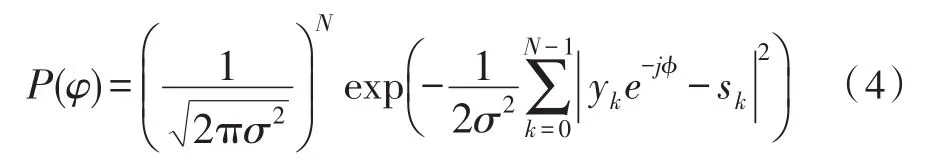
简化式（4），去除无关项：

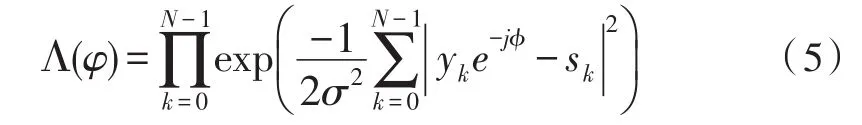
MPSK调制信号的载波相偏盲估计式为：

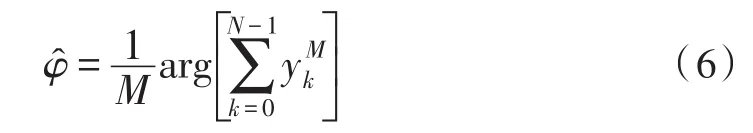
若发送符号sk已知，则数据辅助的载波相偏估计式为：

1.2 相位跳变

当信号的传输时间较短，只进行一次相偏估计就可以。当信号传输时间较长时，再将剩余频偏等效于相偏进行相偏估计是不合理的，误差很大。此时可以将整个传输时间分成若干个短时间段，在每个短时间段内，剩余频偏的影响很小，对每段数据进行相偏估计[6]。但是这种处理方式会引起段与段之间的相位跳变，导致误码率的增大，影响整个系统的通信性能。

针对相位跳变问题，Fitz给出了一种简单方法检测并消除这种跳变，称为Fitz算法[7-8]，假定第i段传输信号内的相位估计为φi，消除相位跳变后的相位为：

其中α≤1。当信噪比较高时，此算法能比较有效的消除相位跳变；但是当信噪比较低时，会频繁地出现相位跳变[9-10]，此时该算法消除相位跳变的能力较差。

文献[11]给出了另一种解决方案，称为Zheng算法，此时表示为：

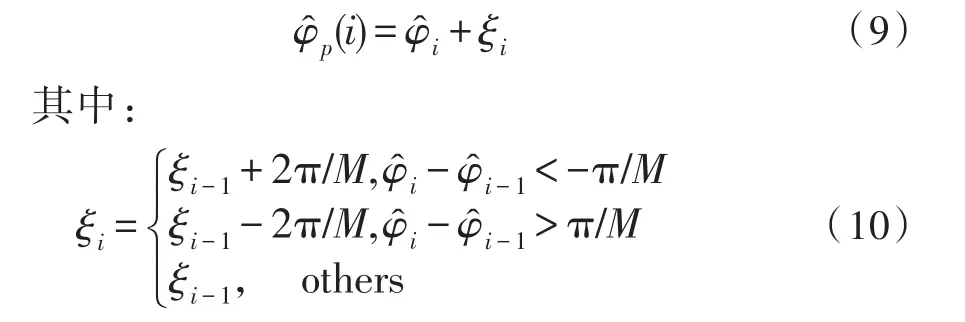
该算法同样存在信噪比较小时会频繁出现相位跳变的问题[12-13]。

1.3 改进的载波相偏估计算法

为了推导改进的载波相偏估计算法，首先对剩余频偏导致的相偏及利用Fitz算法估计的相偏进行仿真，观察相偏的特点。发送信号采用8PSK调制，信噪比为15 dB，剩余归一化频偏为0.000 2，数据长度为40段，每段由32个观察数据组成。

图1 每段估计的相偏曲线图

从图1中可以看出，相偏估计值随机的分布在真实相偏值附近，它的回归曲线是一条直线，这意味着相偏估计值可以近似为：

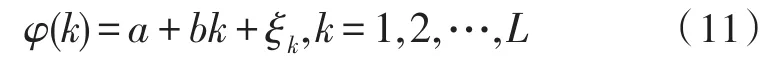
式中，φ(k)为根据第k段观察数据估计的相偏，L为时间段数，φ(1),φ(2),…,φ(L)相互独立，ξk是均值为零、方差为σ2的高斯噪声，a和b为未知常数。如果可以得到a和b的值，就可以通过式（11）预计后面时间段的载波相偏值，以纠正噪声引起的相位跳变[14]。

由于ξk满足高斯分布，且φ(1),φ(2),…,φ(L)间相互独立，得到φ(1),φ(2),…,φ(L)的联合概率密度函数为：

通过最大似然法估计a和b，要使P(a,b)取最大值，只要下式最小：

将式（13）分别对a和b求偏导，并令其为零：

得方程组：

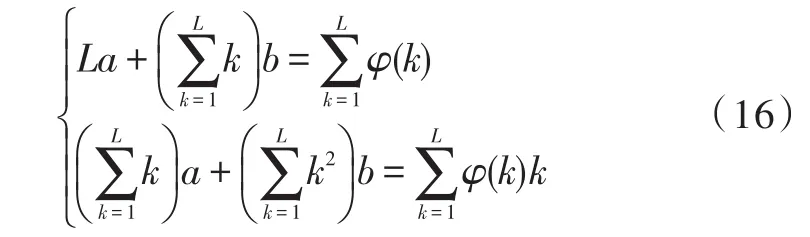
方程组的系数行列式为：

则方程组（16）存在唯一解：

将L段数据作为一组，根据每组数据都可以计算出一条回归曲线[15-16]，设每组得到的回归曲线为：

其中M表示分组数。

假设已经得到第m组的回归曲线，则可以根据回归曲线预测第m+1组的载波相偏值：

另外根据第m+1组的数据计算得到的回归曲线为：

这样对于第m+1组数据来说，根据第m组和第m+1组的回归曲线，对每一段数据，都可以得到这 2个相偏估计值，根据这2个相偏值可以对相位跳变进行修正：

综上所述，本算法的基本流程为：

1）将信号分段，每N个信号序列组成1段，每L段信号组成1组，共有M组；

2）用Fitz算法计算第1组的载波相偏，根据式（18）得到回归曲线，然后根据式（20）得到第1组的最终相偏估计值。

3）假设已得到第i组的最终相偏估计值，利用第i组的回归曲线根据式（21）预测第i+1组的相偏估计值φ′m+1(k)；然后根据第i+1组的数据得到第i+1组的回归曲线，根据式（22）得到另外一组相偏值m+1(k)；最后根据式（23）对相偏进行修正以消除相位跳变得到第i+1组的最终相偏值。

4）重复步骤3）直到信号结束。

2 性能仿真分析

下面通过仿真比较提出的新算法和Zheng算法、Fitz算法的性能。采用8PSK调制信号，总的观察数据长度为1 280个符号，每个时间段包含32个符号，每20段为一组，符号速率fs为240 0baud，剩余载波频偏为0.000 2fs。当SNR分别为15 dB、10 dB时3种算法的估计性能分别如图2、图3所示；当SNR为10 dB时存在相偏及相偏校正后的信号星座图如图4所示；利用3种相偏估计算法校正相偏后系统的误码率性能曲线如图5所示。

图2 SNR=15dB时性能比较

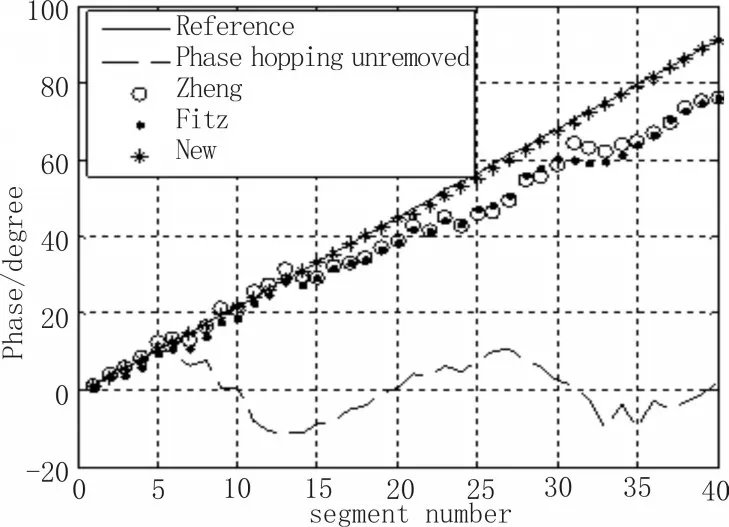
图3 SNR=10dB时性能比较

图4 信号星座图

在图5中的New指的是本文提出的新算法，可以看出，当信噪比较大时Zheng算法和Fitz算法都能够有效地消除相位跳变的影响，但是信噪比较小时，这两种算法都会出现相位跳变现象，严重影响信号解调结果，导致误码率的增高；而新算法不管信噪比大小，都能有效地消除相位跳变的影响，利用此算法校正相偏后的性能和无相偏时的性能基本接近。

3 结束语

考察了频率选择性衰落信道条件下的载波频偏估计算法，由于估计频偏和实际频偏总会存在误差，也就是存在剩余频偏，当时间较短、剩余频偏相对符号速率较小时，可以将剩余频偏处理为相偏，通过考察估计相偏的特点提出了一种新的相偏估计算法，能够有效的实现对相偏的估计与校正。

参考文献：

[1]谢丽君，谭立志.基于FPGA的MSK调制器设计与实现[J].电子设计工程，2012，20（6）:16-18.

[2]孙锦华，韩会梅.低信噪比下时频联合的载波同步算法[J].西安交通大学学报，2015，49（2）:62-67.

[3]刘晓东，陈卫东.一种宽范围高精度的载波频偏估计算法[J].无线电工程，2014，44（3）:43-45.

[4]聂少军，何兵哲，王宏卓.一种新的大载波频偏估计算法[J].电子设计工程，2014，22（1）:168-170.

[5]张帅，张晓林.数字电视大范围载波频偏快逮捕获算法[J].北京航空航天大学学报，2013，39（2）:225-229.

[6]张毅，欧阳志新，邓云凯，等.高性能无数据辅助QPSK频偏估计新算法[J].西安电子科技大学学报，2013，40（2）:187-193.

[7]包超峰，王瑞峰，孔德龙.基于改进Fitz算法的多普勒频移估计方法的研究[J].计算机测量与控制，2014，22（2）:611-613.

[8]张媛.突发数据传输中的同步技术研究[D].南京:南京理工大学，2012.

[9]杨晗竹，李广侠，赵陆文，等.突发信号前向频偏估计方法综述[J].无线电通信技术，2015，41（6）:10-15.

[10]王芳，陈勇，叶志清.一种快速高精度的改进Fitz频率估计算法[J].江西师范大学学报，2014，38（6）:605-609.

图5 存在相偏及相偏校正后的系统误码率

[11]曹亚桃.频偏估计算法研究及FPGA实现[D].天津:天津大学，2014.

[12]孟庆萍，周新力，田伟.基于FFT和长时延自相关函数的频偏估计方法[J].计算机工程与设计，2013，34（3）:799-803.

[13]俞靓.基于相位差的频偏估计技术研究[D].天津:天津理工大学，2013.

[14]孟庆萍，周新力，田伟.一种改进的Fitz载波频偏估计方法及其仿真[J].电讯技术，2012，52（10）:130-132.

[15]谭晓衡，张毛.一种高精度的改进FFT频偏估计算法[J].重庆理工大学学报，2010，1（7）:71-75.

[16]姚国义，李鑫，兰瑞田.一种突发通信信号检测与频偏估计算法[J].无线电通信技术，2014，40（4）:22-23.