基于单胞结构的2.5D碳纤维织物增强复合材料等效热导率
李辉,杜建华,王浩旭
基于单胞结构的2.5D碳纤维织物增强复合材料等效热导率
李辉,杜建华,王浩旭
(陆军装甲兵学院 科研学术处,北京 100072)
采用有限元法分别建立碳纤维束微观结构模型和2.5D碳纤维织物增强碳基复合材料单胞结构模型,计算稳态热边界条件下的碳纤维束等效热导率和碳基复合材料等效热导率,研究碳纤维直径和单丝间距对碳纤维束轴向、径向热导率及碳基复合材料沿厚度方向热导率的影响。结果表明,基体碳的热导率介于碳纤维的径向热导率和轴向热导率之间;纤维束横截面积一定时,随碳纤维直径增大,纤维束轴向热导率升高,径向热导率降低,碳基复合材料沿厚度方向热导率降低;随单丝间距增加,纤维束轴向热导率降低,径向热导率升高,碳基复合材料沿厚度方向热导率升高。
等效热导率;有限元法;2.5D织物;碳基复合材料;碳纤维
碳纤维增强碳基复合材料是以树脂碳或沉积碳为基体,以碳纤维为增强体制备的低密度、耐高温复合材料。并具有高而稳定的摩擦因数,良好的耐磨性和整体性,可应用于车辆离合器和制动器用湿式摩擦材料。在摩擦副结合过程中,摩擦材料较好的导热性能可降低摩擦热的积累,使其更好地适用于高能量密度传动系统。对于材料热导率的计算,国内外学者提出了多种经典方法,如等效介质理论[1],Maxwell-Euck模型[2],Nielsen模型[3]和自洽方法[4]等。近年来,基于试验技术[5−8]和计算机技术[9−11]的发展,关于等效热导率的研究取得了很多成果[12]。江华等[13]利用微观结构图像识别技术与有限元分析相结合,研究了缺陷位置、占比和厚度对复合材料等效热导率的影响。结果表明,考虑缺陷后等效热导率降低约52.1%。陆思达等[14]采用有限元法计算了平纹编织C/SiC复合材料的等效热导率,并指出材料热导率随孔隙率的增大而降低。聂荣华等[15]提出了一种基于二维编织结构的等效热阻法复合材料热导率预测模型,并研究了结构参数对材料热导率的影响。庞旭明等[16]利用最小热阻法和并串联模型计算了含孔隙和截面热阻的复合材料等效热导率,且计算值与实验值一致性较好。张彪等[17]提出了一种针对二维多孔材料的快速导热系数计算方法,该方法不仅考虑了孔隙率和孔径因素,还考虑了温度和热辐射的影响。FAROOQI等[18]利用有限元模拟方法计算了陶瓷基复合材料的热导率,模拟结果与试验值吻合较好。本文采用有限元法对2.5D碳纤维织物增强复合材料等效热导率进行预测,并在此基础上通过改变纤维直径与单丝间距,研究纤维束结构对材料导热性能的影响规律,为复合材料的制备提供参考。
1 几何模型
以碳纤维(T300,日本东丽公司)2.5D浅交弯联织物为增强体,采用酚醛树脂(山东圣泉新材料有限公司)浸渍碳化,制备碳纤维增强碳基复合材料(即C/C复合材料)。
由碳纤维增强碳基复合材料横截面SEM照片(图1(a))可知,复合材料由碳纤维束和碳基体构成,其中碳纤维束截面呈扁平跑道型,纬纱碳纤维束平直排列,经纱碳纤维束一次穿越两层纬纱,跨越一股纬纱后回到初始平面形成2.5D浅交弯联结构。根据实测尺寸,建立图1(b)所示的2.5D浅交弯联碳纤维织物增强复合材料单胞结构模型。单胞长4 mm,宽0.82 mm,厚1.15 mm;纬纱截面宽l=1.2 mm,厚h=0.1 mm;经纱截面宽l=0.8 mm,厚h=0.15 mm;纬纱间距0.8 mm。
图2(a)所示为碳纤维束的截面SEM照片。由图可知,碳纤维束中圆形截面的碳纤维单丝紧密排列,单丝之间填充碳基体。假设单丝在纤维束中呈直线分布,则可建立碳纤维束的微观模型如图2(b)所示。其中,碳纤维直径=7 μm,两根碳纤维之间距离=0.2 μm,横截面宽=7.2 μm,长= 12.47μm。纤维束中碳纤维体积分数w=85.68%,基体碳体积分数w=14.32%。
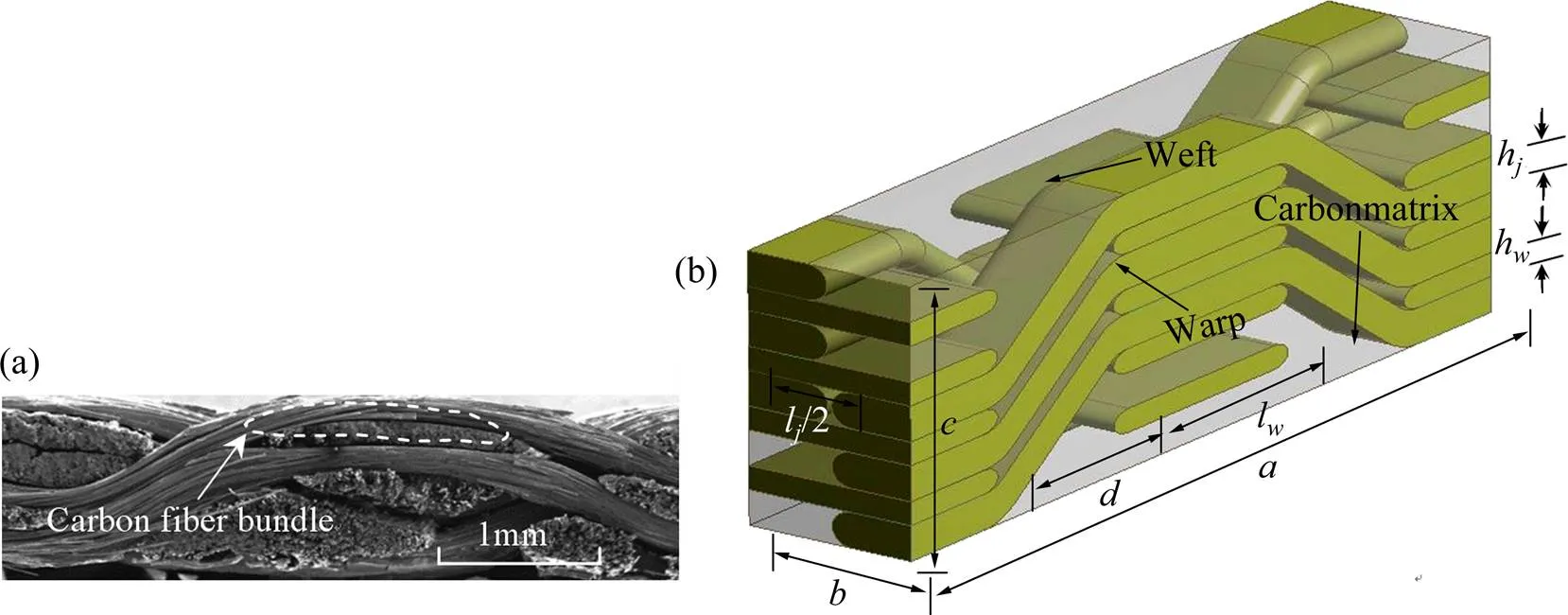
图1 2.5D浅交弯联碳纤维织物增强碳基复合材料

图2 碳纤维束的截面SEM形貌与微观模型
2 热导率计算
2.1 等效热导率定义
由傅里叶定律可知:
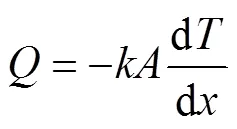
式中:为热导率,W/(m∙K);为热流量,J/s;A为导热面积,m²;d/d为温度梯度,K/m。
如果温度梯度为常数,则可定义k为等效热导率,则轴方向的等效热导率为:
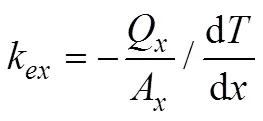
式中:A为垂直方向的表面积,Q为通过方向的等效热流量。
利用ANSYS Workbench软件稳态热分析模块对模型施加固定温度边界条件(即第1类边界条件),可得稳定的温度梯度和热流密度分布q,进而求得等效热流量:
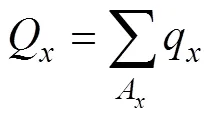
2.2 碳纤维束等效热导率计算
碳纤维束由纤维与基体碳组成,其中碳纤维热物性参数呈现明显的各向异性,径向热导率(4.9 W/(m·K))约为轴向热导率(40 W/(m·K))的1/8;基体碳为各向同性材料,实验室测得纯树脂碳热导率约为20 W/(m·K)。
在碳纤维束微观模型两个相对表面上分别加载恒定温度1 100和100 ℃,其它面设为绝热。依次计算,,方向的稳态导热情况。图3至图5分别给出了3个方向上温度与热流密度的分布状况,详细计算结果如表1所列。由等效热导率计算结果可知,方向与方向的热导率几乎相等,温度与热流密度分布不均匀,热流密度最大值出现在碳纤维之间的基体碳处;方向热导率数值较大,温度分布由高温端向低温端均匀递减,热流密度在碳纤维与基体碳中有明显的分布 界线。
这是因为在、方向,碳纤维与基体碳的分布形式与体积分数相同,且基体碳热导率大于碳纤维径向热导率,热流更易通过基体碳传导。方向碳纤维与基体碳并联排列,两者由于热导率的不同形成各自的热流通路。碳纤维轴向热导率较高,所以纤维束z方向热导率较高。

表1 碳纤维束等效热导率计算结果
2.3 复合材料等效热导率计算
2.5D浅交弯联碳纤维织物增强复合材料单胞模型中,碳纤维束热导率采用表1数据,沿碳纤维束轴向热导率为37.146 W/(m·K),沿碳纤维束横截面方向热导率为6.212 5 W/(m·K)。
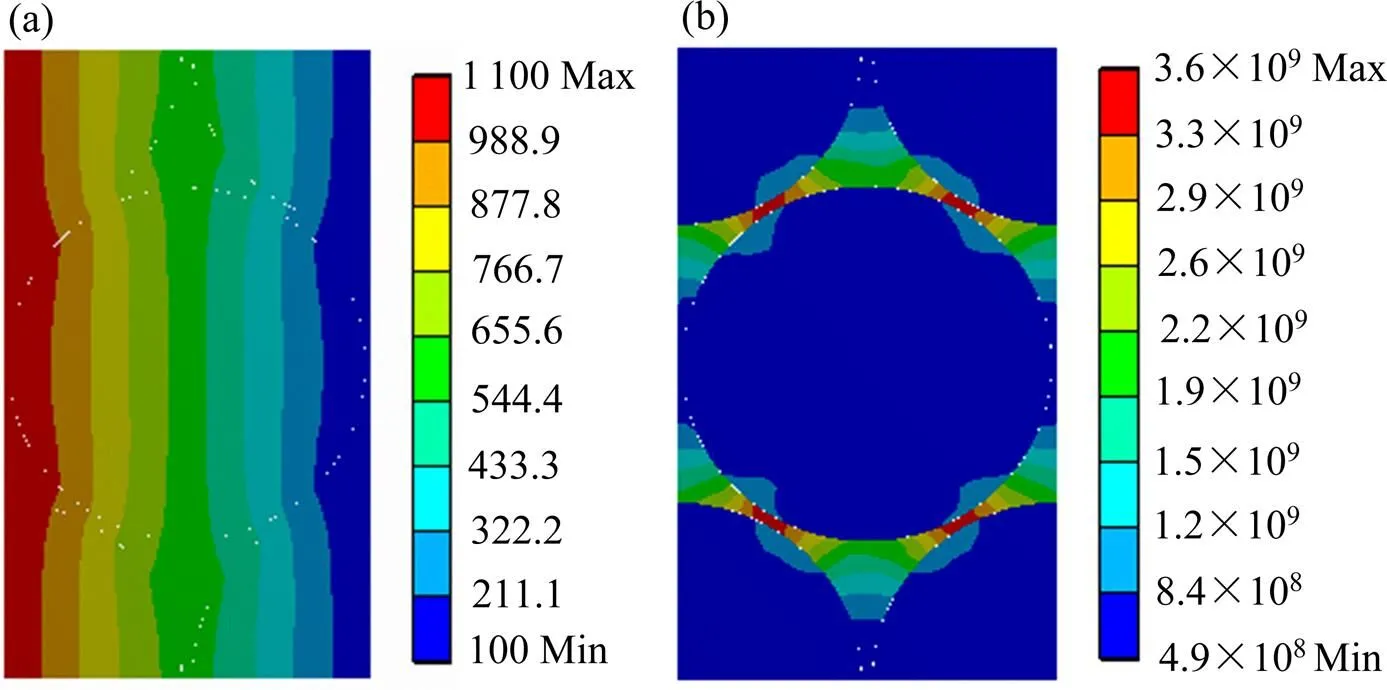
图3 x方向温度与热流密度分布
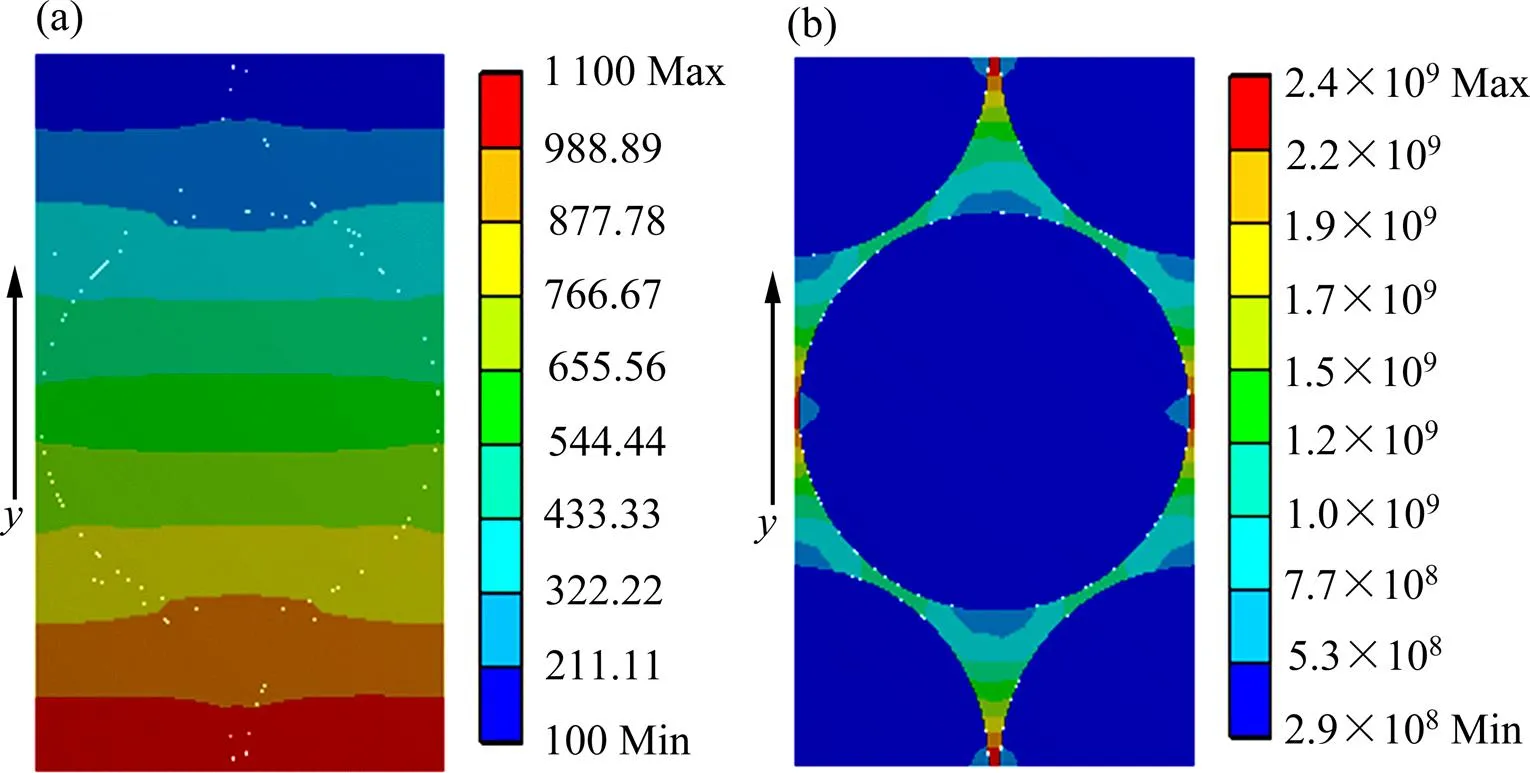
图4 y方向温度与热流密度分布
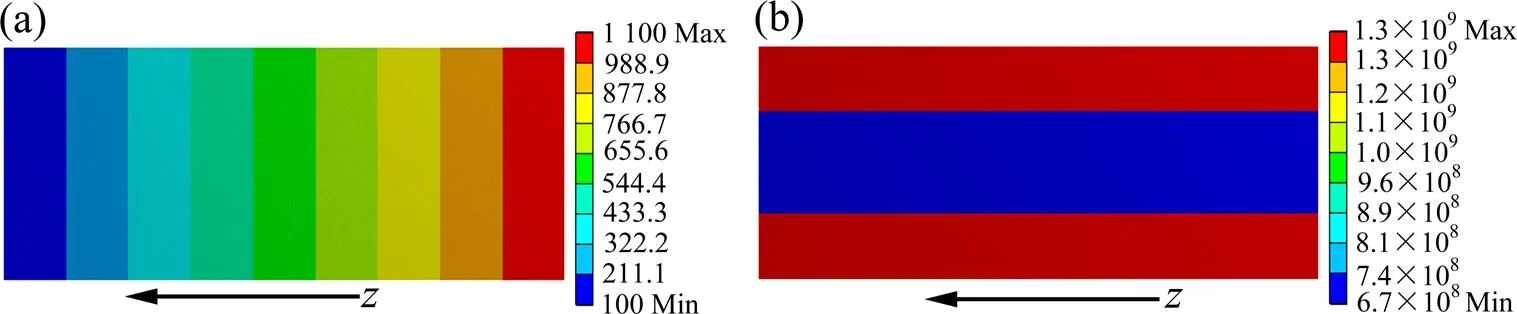
图5 轴向温度与热流密度分布
试验所制备的碳纤维增强碳基复合材料为低密度多孔材料,由图1(a)可知,孔隙分布于纤维束之间的基体碳处。取基体碳热导率为0.5 W/(m·K)[19]。施加边界条件与碳纤维束等效热导率计算时相同,在模型两个相对表面上分别加载恒定温度1 100和1 00 ℃,其它所有面设为绝热。
碳纤维增强碳基复合材料用作摩擦材料使用时,主要关心其沿厚度方向(方向)的热导率。图6给出了沿厚度方向施加稳态温度边界时,复合材料单胞结构温度与热流密度分布,详细计算结果如表2所示。由图可知,温度与热流密度分布不均匀,沿经纱碳纤维束的热流密度值明显大于沿纬纱碳纤维束和基体碳的热流密度值。这是因为沿经纱碳纤维束的轴向的热导率较大(37.146 W·m−1·K−1),形成了快速热流通道。

表2 单胞等效热导率计算结果
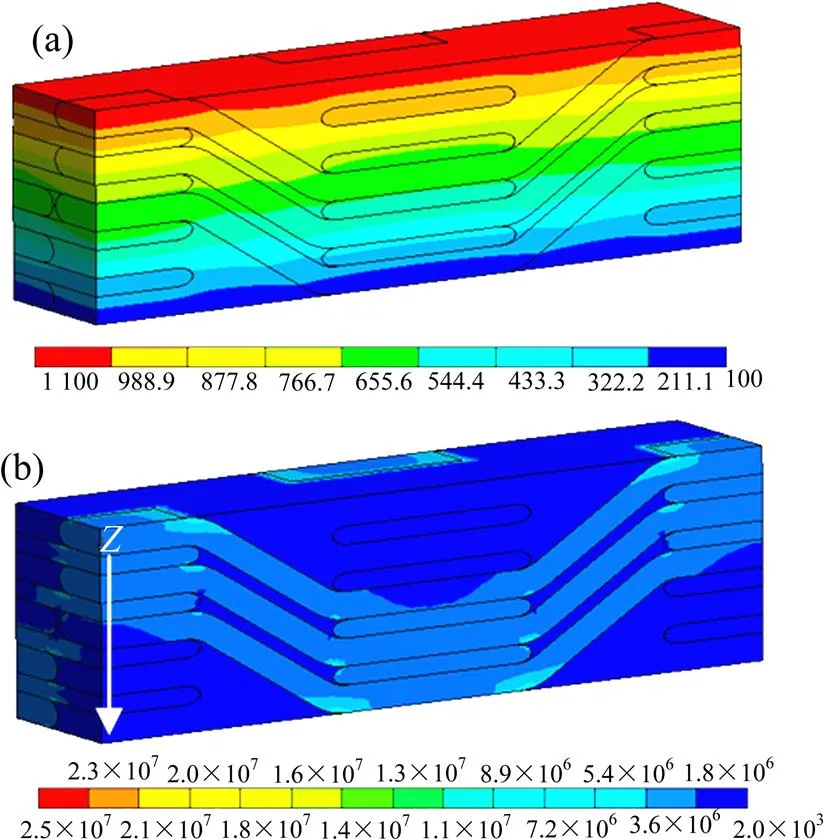
图6 厚度方向温度与热流密度分布
3 结构参数对等效热导率的影响
3.1 单丝间距的影响
保持各组分材料热导率与碳纤维单丝结构不变,改变碳纤维单丝间距,重新计算碳纤维束等效热导率和复合材料等效热导率。碳纤维单丝间距变化范围0.05 μm至0.5 μm,计算步长0.05 μm。图7所示为碳纤维束等效热导率随单丝间距的变化。由图可知,随单丝间距增大,纤维束轴向热导率k降低而径向热导率k升高。这是因为在纤维束中,基体碳的热导率大于碳纤维径向热导率而小于碳纤维轴向热导率。单丝间距增大,纤维束中碳纤维体积分数降低,沿轴向热导率高的碳纤维相对减少,基体碳体积分数升高,所以纤维束轴向热导率降低;沿径向热导率低的碳纤维相对减少,基体碳体积分数升高,所以纤维束径向热导率升高。
图8所示为复合材料厚度方向热导率随纤维间距的变化曲线。由图8可知,复合材料沿厚度方向的热导率随单丝间距的增大而升高,与纤维束径向热导率变化趋势相同。这是因为在2.5D织物结构中,绝大部分纤维束的径向与复合材料的厚度方向一致,基体碳热导率不变,复合材料厚度方向热导率主要受纤维束径向热导率影响。
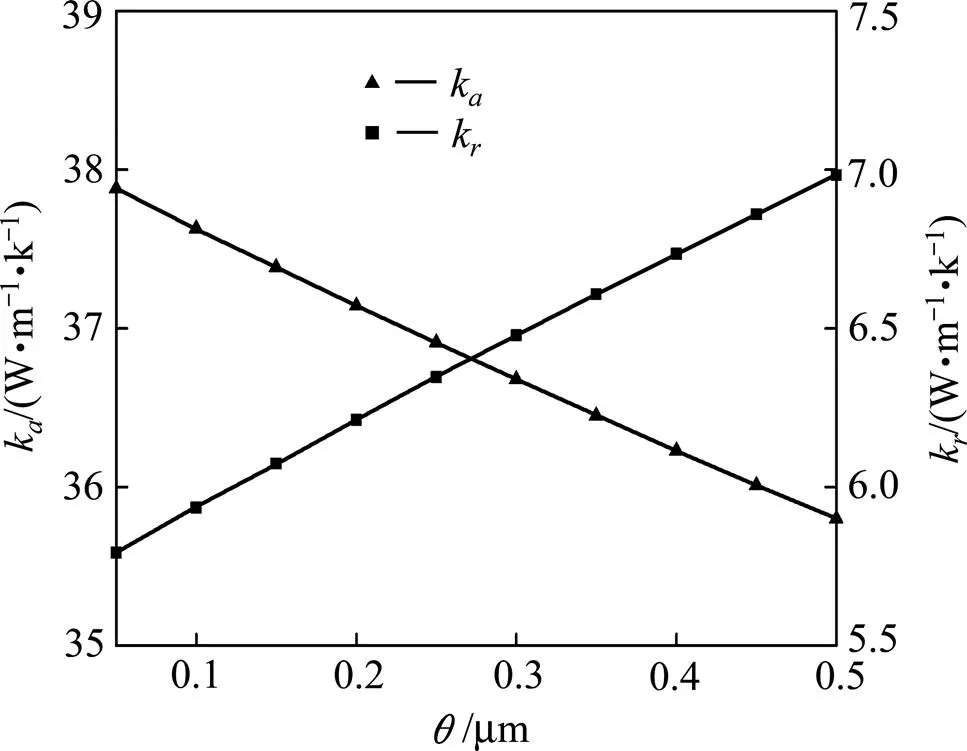
图7 碳纤维束热导率随纤维间距的变化
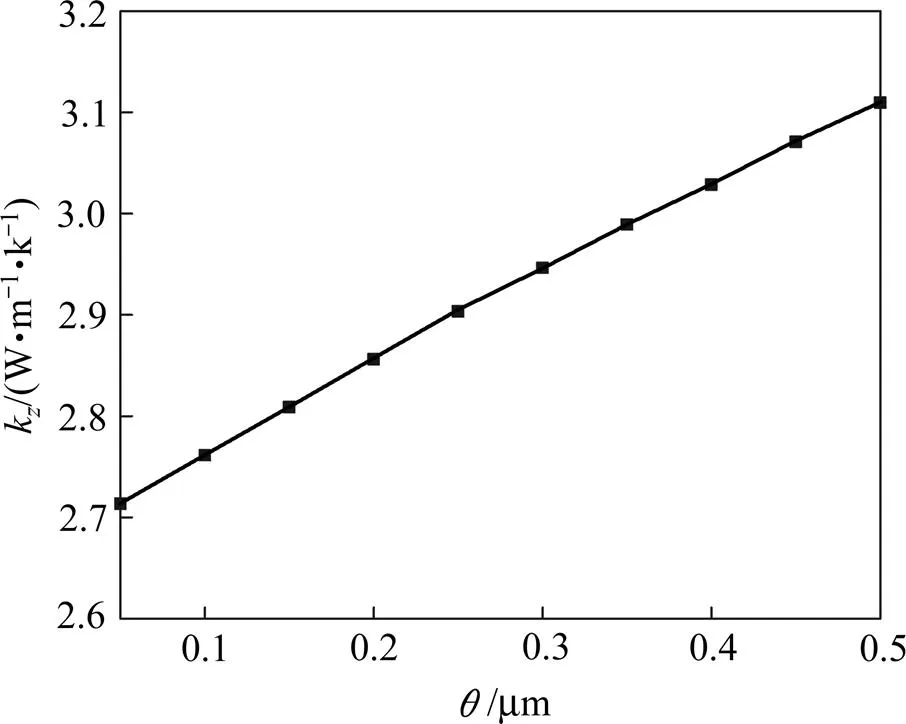
图8 复合材料厚度方向热导率随纤维间距的变化
3.2 碳纤维直径的影响
保持各组分材料热导率和碳纤维单丝间距不变,改变碳纤维直径,重新计算碳纤维束等效热导率和复合材料等效热导率。碳纤维直径变化范围5 μm至10 μm,计算步长0.5 μm。图9所示为碳纤维束等效热导率随纤维直径的变化。由图可知,随纤维直径增大,纤维束轴向热导率k升高而径向热导率k降低。这是因为随纤维直径增大,纤维束中碳纤维体积分数增大,沿轴向热导率高的碳纤维相对增多,基体碳体积分数降低,所以纤维束轴向热导率升高;沿径向热导率低的碳纤维相对增多,基体碳体积分数降低,所以纤维束径向热导率降低。
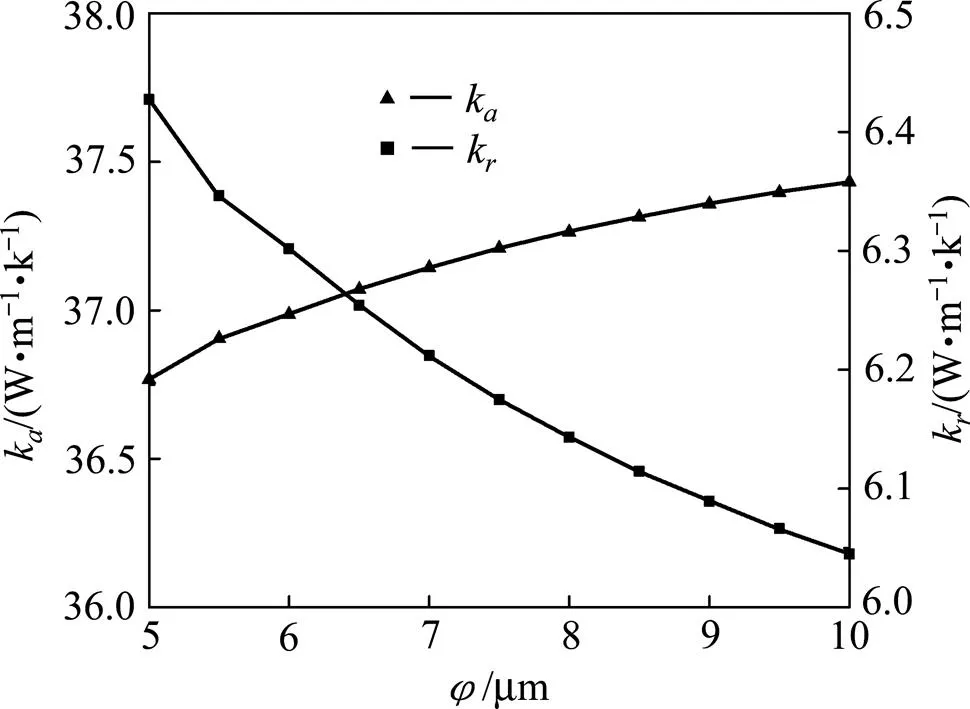
图9 碳纤维束热导率随碳纤维直径的变化
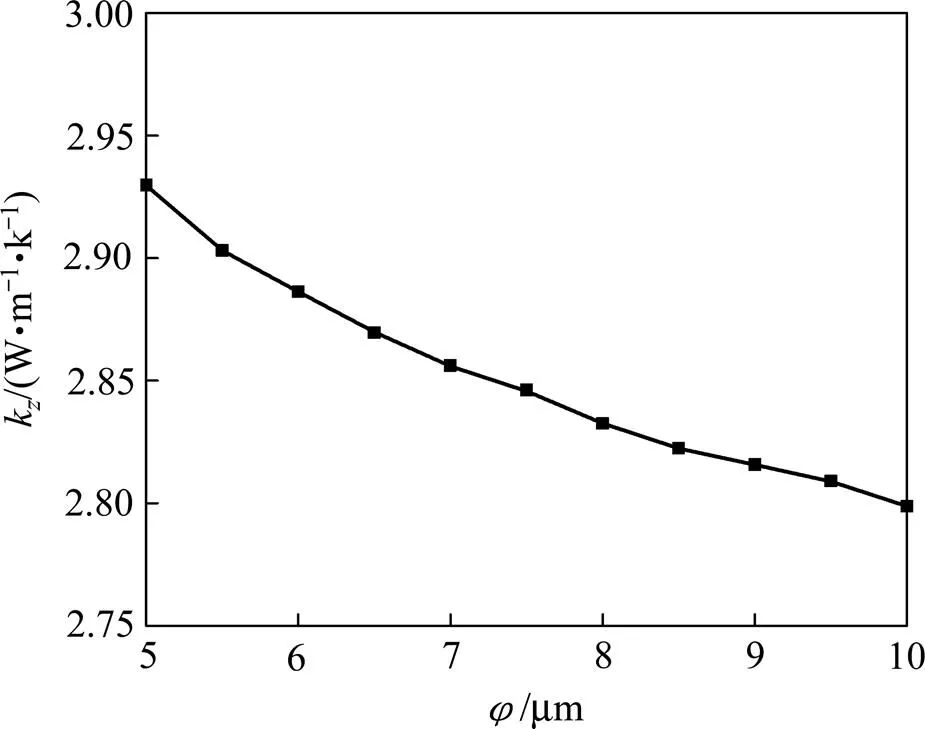
图10 复合材料厚度方向热导率随碳纤维直径的变化
如图10所示,复合材料沿厚度方向热导率随纤维直径的增大而降低。这是因为复合材料厚度方向热导率主要受纤维束径向热导率影响,其变化趋势与碳纤维束径向热导率变化趋势一致。
4 结论
1) 利用有限元法建立碳纤维2.5D浅交弯联织物增强碳基复合材料单胞结构模型,可实现等效热导率的计算。
2) 碳纤维束横截面积一定时,纤维束径向热导率随单丝间距的增加而升高,随碳纤维直径的增大而降低;纤维束轴向热导率随单丝间距的增加而降低,随碳纤维直径的增大而升高。
3) 2.5D浅交弯联织物增强复合材料沿厚度方向的热导率随纤维间距的增大而升高,随着碳纤维直径的增大而降低。
[1] ROLP L. The electrical resistance of binary metallic mixtures[J]. Journal of Applied Physics, 1952, 23(7): 779−784.
[2] HASHIN Z, SHTRIKMAN S. A variational approach to the theory of the effective magnetic permeability of multiphase materials[J]. Journal of Applied Physics, 1962, 33(10): 3125− 3131.
[3] LAWRENCE E, NIELSEN. Generalized equation for the elastic moduli of composite materials[J]. Journal of Applied Physics, 1970, 41(11): 4626−4627.
[4] TORQUATO S, HASLACH H. Random Heterogeneous Materials: Microstructure and Macroscopic Properties[M]. New York: Springer, 2002, 55(4): B62.
[5] 孔清, 樊桢, 余立琼, 等. 高导热C/C复合材料发展现状[J].宇航材料工艺, 2014, 44(1): 16−23.KONG Qing, FAN Zhen, YU Liqiong, et al. Progress of high- thermal conductivity carbon/carbon composites[J]. Aerospace Materials & Technology, 2014, 44(1): 16−23.
[6] 易法军, 张巍, 孟松鹤, 等. 复合材料高温热物理性能实验研究[J]. 宇航学报, 2002, 23(5): 85−88. YI Fajun, ZHANG Wei, FENG Songhe, et al. An experimental study on thermophysical properties of C/C composites at elevated temperature[J]. Journal of Astronautics, 2002, 23(5): 85−88.
[7] MANEL H, BOUDJEMAA A, ABDERRAHIM B. Thermal conductivity of polymer/carbon nanotube composites[J]. Materials Science Forum, 2012, 714(3): 99−113.
[8] BA N, CHARLES H, HENAGER J. Fiber/matrix interfacial thermal conductance effect on the thermal conductivity of SiC/SiC composites[J]. Journal of Nuclear Materials, 2013, 440(1): 11−20.
[9] 李丽, 肖红, 程博闻, 等. 基于瞬变平面热源法的纤维热导率测试[J]. 纺织学报, 2016, 37(12): 18−23. LI Li, XIAO Hong, CHENG Bowen, et al. Testing of thermal conductivity of fiber based on transient plane heat source method[J]. Journal of Textile Research, 2016,37(12): 18−23.
[10] 常晓权, 郑钢铁. 复合多层混合结构三维热传导分析[J]. 应用力学学报, 2005, 22(4): 633−637. CHANG Xiaoquan, ZHENG Gangtie. Three dimensional heat transfer analysis to hybrid multilayer composite structure[J]. Chinese Journal of Applied Mechanics, 2005, 22(4): 633−637.
[11] ZHI Haifeng, JIA Yunzhi, ZHEN Fan, et al. An analytical model of thermal conductivity for carbon/carbon composites with pitch-based matrix[J]. Advances in Mechanical Engineering, 2014, 2014(1): 1−12.
[12] 梁珩, 童明波, 王玉青, 等. 细编穿刺C/C复合材料热导率数值模拟[J]. 固体火箭技术, 2017, 40(3): 364−372. LIANG Heng, TONG Mingbo, WANG Yuqing, et al. Simulation on effective thermal conductivity of fine weave pierced C/C composite[J]. Journal of Solid Rocket Technology, 2017, 40(3): 364−372.
[13] 江华, 毛军逵, 屠泽灿, 等. 基于微结构识别的单向复合材料导热系数预估[J]. 航空动力学报, 2016, 31(11): 2642−2651. JIANG Hua, MAO Junkui, TU Zecan, et al. Thermal conductivity prediction of unidirectional composites based on microstructure identification[J]. Journal of Aerospace Power, 2016, 31(11): 2642−2651.
[14] 陆思达, 高希光, 宋迎东. 基于有限元法的平纹编织C/SiC复合材料等效导热系数预测方法[J]. 航空动力学报, 2014, 29(7): 1574−1582.LU Sida, GAO Xiguang, SONG Yingdong. Prediction method on equivalent thermal conductivity coefficient of plain braided C/SiC composites material based on finite element method[J]. Journal of Aerospace Power, 2014, 29(7): 1574−1582.
[15] 聂荣华, 矫桂琼, 王波. 二维编织C/SiC陶瓷基复合材料的热传导系数预测[J]. 复合材料学报, 2009, 26(3): 169−174.NIU Ronghua, Jiao Guiqiong, WANG Bo. Prediction on thermal conductivity for 2D braided C/SiC composites[J]. Acta Materiae Compositae Sinica, 2009, 26(3): 169−174.
[16] 庞旭明, 周剑秋, 杨晶歆, 等. 含孔隙及界面热阻的复合材料有效导热系数[J]. 中国有色金属学报, 2016, 26(8): 1668−1674.PANG Xuming, ZHOU Jianqiu, YANG Jingxin, et al. Effective thermal conductivity of composite materials containing pore and interface thermal resistance[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(8): 1668−1674.
[17] 张彪, 齐宏, 阮立明. 二维多孔热密封材料的有效导热系数模拟[J]. 工程热物理学报, 2012, 33(7): 1229−1232.ZHANG Biao, QI Hong, RUAN Liming. Two-dimensional simulation for the effective thermal conductivity of heat-sealing porous material[J]. Journal of Engineering Thermophysics, 2012, 33(7): 1229−1232.
[18] FAROOQI J K, SHEIKH M A. Finite element modelling of thermal transport in ceramic matrix composites[J]. Computational Materials Science, 2006, 37(3): 361−373.
[19] 邵海成, 刘桂武, 乔冠军, 等. 低密度炭/炭保温材料导热性能的影响因素[J]. 材料科学与工程学报, 2013, 31(5): 627−631. SHAO Haicheng, LIU Guiwu, QIAO Guanjun, et al. Factors affecting thermal conductivity of low-density carbon/carbon insulation materials[J]. Journal of Materials Science & Engineering, 2013, 31(5): 627−631.
(编辑 高海燕)
Equivalent thermal conductivity of composites reinforced bycarbon fiber with 2.5D fabric based on unit cell
LI Hui, DU Jianhua, WANG Haoxu
(Department of Science Research, Academy of Army Armored Force, Beijing 100072, China)
The microstructure model of carbon fiber bundles and the unit cell structure model of the composites reinforced by carbon fiber with 2.5D fabric were established by finite element method. The equivalent thermal conductivity of carbon fiber bundles and composites in steady thermal conditions were calculated. The effects of carbon fiber diameter and the space between two carbon fibers on the thermal conductivity in axial and radial direction of carbon fiber bundles and in thickness direction of the composites were investigated. The results show that, the thermal conductivity of the carbon matrix is between the radial thermal conductivity and the axial thermal conductivity of carbon fiber. With increasing the carbon fiber diameter, the axial thermal conductivity of the carbon fiber bundles increases, the radial thermal conductivity and the thermal conductivity of the composites in thickness direction decrease. With increasing the space between two carbon fibers, the axial thermal conductivity of the carbon fiber bundles decreases, the radial thermal conductivity and the thermal conductivity of the composites in thickness direction increase.
equivalentthermal conductivity; finite element method; 2.5D fabric; carbon matrix composites; carbon fiber
TH117; TB322
A
1673-0224(2018)01-94-07
国家自然科学基金资助项目(51001117);军队科研计划项目
2017−10−13;
2017−11−05
杜建华,助理研究员,博士。电话:13552902286;E-mail: dih619@sina.com

