地埋式自升起喷灌装置设计原理分析

谢崇宝，张国华，彭文启，王伟杰

（1.中国灌溉排水发展中心，北京 100054；2.中国水利水电科学研究院 水环境研究所，北京 100038）

1 概述

目前，美国、欧洲等发达国家和地区大多采用大型喷灌机和绞盘式喷灌机等既节约劳力、又有利于规模化灌溉的喷灌技术［1-4］，较少采用固定管道式喷灌这种影响农田机械化耕作和收割的灌溉方式。而在我国，固定管道式喷灌是推进高效节水灌溉发展的重点之一，因此解决其影响耕作、频繁拆卸、仓储损耗等问题具有十分重要而又紧迫的现实意义。

园林绿化中常用的埋藏式喷头和大田中常用的摇臂式喷头，均不能直接接触土壤。埋藏式喷头，需要一个直达地表的保护管，将喷头安装在这个保护管内，防止外部土壤和杂物进入管内堵塞喷头。但若将其用于农田灌溉中，因种植农作物的土地需要季节性翻耕，这个保护管会对耕作活动造成障碍，不利于农业机械化、规模化耕作。摇臂式喷头，自身结构的限制只能安装在地面以上，需要灌溉时进行逐个安装，农作物收割前或土层翻耕时需要将其逐个拆卸并放回仓库中，不仅影响耕作，而且工作强度和工作量巨大，工作效率低，用工成本高，不符合农业现代化的发展需求。

为此，作者基于理论和实践有机融合的设计理念，以不影响耕作为目标，以将喷头直接埋入土中的方法来解决固定喷灌影响机械化耕作问题的设想，分析得出这种喷头不仅要能够实现喷洒而且要具备破土功能的实际需求和设计思路，成功研发了地埋式自升起喷灌装置［5-7］。本文基于该设备实际破土过程中的阻力和推动力分析，重点研究地埋式自升起喷灌装置的顶出机理。

2 地埋式自升起喷灌装置受力结构分析

地埋式自升起喷灌装置要同时具备破土和喷洒功能，必须在结构设计上寻求技术突破。图1为地埋式自升起喷灌装置的核心部件图，侧端出水口实现喷洒功能，顶端出水口实现破土功能，从而实现一种设备“地下为钻头、地上为喷头”的双重功能且能够自动切换。本文重点研究装置的破土机理，有关喷头的结构优化与水力设计参数问题，将另文研究。

图1 喷头模型

地埋式自升起喷灌装置依托内部水压形成向上破土推动力，同时受到埋深（即地埋设备顶部在耕作土壤中的深度）土的自重力、土体对管道侧壁的摩擦力以及土体抵抗剪切破坏的3种力的作用。地埋设备向上破土受力如图2所示。建立坐标系：以套管上沿为基准，设定z=0，即伸缩管向上顶土的起始位置，图中为伸缩管顶土高度为z时的示意图。设地埋装置在耕作土壤中的埋深为h=0.4m，伸缩管直径d=0.05 m，垂向方向顶土的面积伸缩管侧面积S2=πdz。

图2 地埋式自升起喷灌装置顶土过程受力分析

2.1 有效推动力 破土有效推动力W推导如下：系统底部的输水压强P0，喷头出水而损失的压强即管内局部损失Ps，伸缩管内水柱的压强Pw三者相减即为作用在伸缩管顶部的有效压强，再乘以伸缩管的截面积S1，得到伸缩管道的向上推力。设定伸缩管自身的重量为Gp，最终得到破土的有效推动力W为

根据局部损失室内实验分析测定［8］，换算出不同工况条件下水平喷头处的实际顶推压强，以及压强损失量Ps，如表1所示。

表1 不同进口流量压力下装置的有效压强换算

由最优线性拟合可以得到有效压强P0-Ps与进口压强P0的关系式为（单位Pa）

从装置底部到伸缩管顶部的高度约为1.3 m，则水柱最大高度为1.3 m，则伸缩管水柱的压强Pw=12 740 Pa，式（1）可表示为：

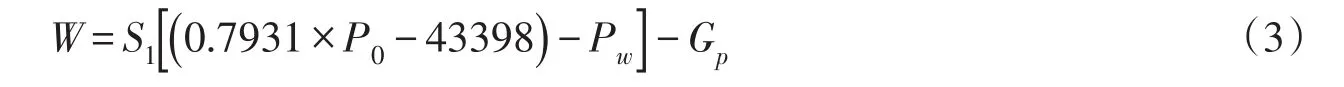
2.2 重力 在垂向方向土的自重应力为：

由式（4）可知随着埋深越大，土的自重应力越大，σz为土的自重应力（N/m2），γ为土的容重（N/m3），则管道在破土过程中（0≤z≤h）所受到土体重力作用为：

伸缩管道在最底部（即z=0处）受到土体最大重力，其表达式为：

2.3 摩擦力 在破土过程中，由于土体侧向压力的存在，管道侧壁与土体产生相对滑动时，将会受到土体对其的摩擦阻力作用。

首先分析伸缩管道受到的侧向应力，从图1可以看出，随着埋深越大，侧向应力也随之越大，伸缩管道顶部z处的侧向应力为：

z=0处的侧向应力为：

式中：σx为侧向应力，N/m2；K为土的侧向应力系数。如图1的右侧受力分析所示，侧向应力呈线性分布，可得伸缩管道受到的平均应力为：

则伸缩管道受到的压力N为：

根据摩擦定理，破土过程中（0≤z≤h）管道受到的摩擦力N为：

当伸缩管刚开始顶出地面（即z=h），管道受到最大的侧向应力，即受到最大摩擦力F为：

2.4 剪切力 在伸缩管工作的过程中，土体被逐层剪切破坏。根据摩尔-库伦破坏准则，对于黏性土壤，抗剪强度公式为：

式中：τf为土壤的抗剪强度；cf为土壤的黏聚力；σ为滑动面上的法向应力；φ为土壤的内摩擦角，即为抗剪强度线的倾角。

对伸缩管顶部土体进行受力分析，如图3所示，侧向应力为σx，垂向应力为土重力加上顶管对土体施加的力σz+σT，根据应力圆与土体抗剪强度公式的关系，可得将土体剪切破坏所需要满足的关系式为：

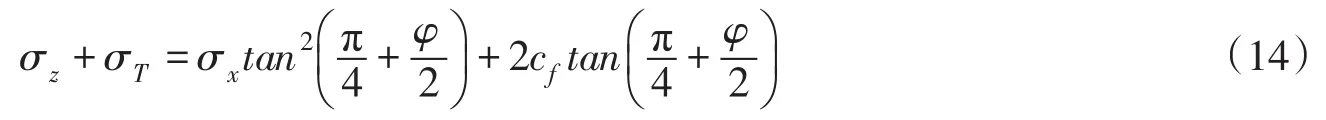
由于最初破土阶段所需的剪切力是最大的，故σz和σx取埋深h=40 cm处的土重力和侧向应力。

图3 未浸润土体在伸缩管作用下的受力图

则将土进行剪切破坏所需的最大剪切力为：

2.5 阻力合力 为了简便起见，要实现灌溉设备的破土过程，需克服土体最大重力Gmax、最大摩擦力fmax以及最大的土体剪切破坏力Tmax，即：

考虑有不确定因素存在，例如灌溉设备中内外套管之间存在的摩擦阻力等，为保证管道可以顺利破土而出，设定阻力余量系数为β=1.05，可得破土所需克服的最小阻力Fmin为

3 地埋式自升起喷灌装置顶出分析

3.1 最小进水压强计算公式 破土所需要的条件为破土推动力大于或等于其受到的阻力，即

将式（3）代入上式，即可得到系统输入压强要满足的条件，而所有的动力均来源于管道输水压力：

故最小的输水压强为：

实际情况中的耕种土壤有多种类型，或是多种土壤类型的混合。为了理论分析，这里选用均匀松砂、均匀紧砂、有机质软黏土以及压实情况下的有机质软黏土为研究对象，分析推求不同类型土壤对灌溉装置的阻力，以及破土所需的最小输水压强。

3.2 无出流的顶管破土所需最小进水压强 为了研究顶管出流对地埋式自升起喷灌装置破土能力的影响，本文计算了顶管不出流工况下的最小进水压强，计算结果见表1。

由于顶管顶部土体未被浸润，故土体的重度选用干重度；摩擦力系数取0.5；对于砂土的侧向应力系数取0.3～0.5，对于黏土的侧向应力系数取0.5～1.0，而压实状态的黏土取0.5～3.0；砂土的黏聚力为零，黏土的黏聚力取20～60 kPa，砂土的内摩擦角取36°～45°，黏土的内摩擦角取30°～45°，另外顶管自重为20 N。综合考虑各种因素的影响，各参数取值如表2所示。

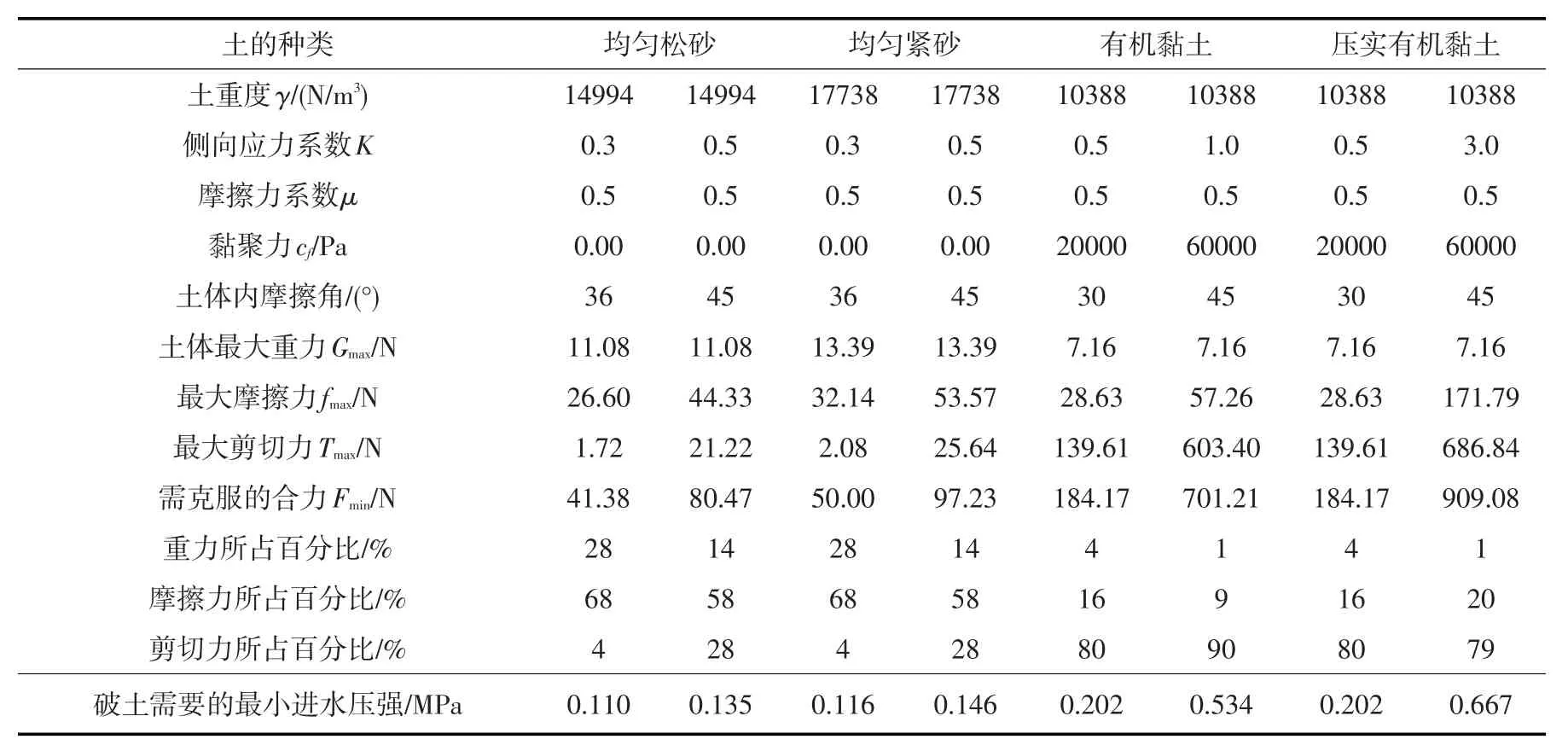
表2 无出流的管道破土所需的最小进水压强计算

根据表2，采用式（17）计算可得，在均匀松砂情况下，破土所需要的阻力最小，为41.38 N；而在压实情况下的有机黏土（极端情况），破土所需要的力最大，为909.08 N。对于均匀松砂，破土所需要的最小进水压强为0.11 MPa，对压实的有机黏土情况下，破土所需要的输水压强竟然高达0.667≈0.7 MPa，远高出喷灌实际工作压力。并且从上表中可以看出，从松砂到紧砂，从一般有机黏土到压实的有机黏土，剪切力所占的百分比逐步增加；对于有机黏土而言，剪切力占合力79%～90%，说明要在黏土中实现破土而出，主要需要克服土体的剪切力。

3.3 有出流的顶管破土所需最小进水压强 针对地埋设备的有出流的伸缩管，由于破土过程中土体在水流的作用下逐渐丧失黏聚力［9］，所以破土所需要的水压相比传统顶管会大幅减小。对于黏性土壤，地埋设备破土过程中的喷水，使得土体的黏聚力随着含水量的增加而迅速减小［10-11］，砂土的黏聚力为零，为计算方便，土壤的黏聚力取15 kPa［12-13］，则根据式（15）可得将土进行剪切破坏所需的剪切力为58.9 N。

对于土体重度，由于顶管出流将使其周围的土体趋于饱和，而远离顶管的土体受其影响较小，所以这里采用80%的干重度加上20%的饱和重度作为破土过程中土体的综合重度。对于摩察系数，试验研究表明，不同类型、不同含水量状态下的土壤对不同材料间的摩擦系数有着显著差异，地埋设备的材质为超高分子量聚乙烯，其摩擦系数介于0.3～0.5之间。对于侧向应力系数，由于土体含水量在顶管出流的作用下迅速增加，土体接近饱和液化，侧向应力系数也会比通常情况小，这里采用0.1～0.2，对于压实有机黏土的侧向应力系数最大取到0.4；另外顶管自重为20 N。综合考虑各种因素的影响，各参数取值如表3所示。

根据表3，采用式（17）计算可得，在均匀松砂情况下，破土所需要的力最小，为18.3 N；而在压实情况下的有机黏土（极端情况），破土所需要的力最大，为97.82 N。从表2中可以看出：对于均匀松砂，破土所需要的最小进水压强为0.095 MPa，对压实的有机黏土情况下，即地埋设备破土最为不利的状态，当输水压强达到0.146 MPa时，该地埋设备可以顺利破土而出，达到正常工作状态。也就是，在最不利的土壤条件下，只要灌溉输水压强达到0.15 MPa以上即可满足地埋式自升降高效节水灌溉设备的正常工作。

表3 有出流的管道破土所需的最小进水压强计算

同时，从上表可以看出：由松砂到紧砂，由一般黏土到压实黏土，各个阻力所占百分比也在发生变化。对于黏性土壤，剪切破坏力所占的比重在60%～80%之间，起到决定性作用。从另一角度而言，对于黏土能否顺利破土，主要取决于剪切破坏力；对于砂质土壤能否顺利破土，主要克服土体重力和摩擦力。

4 伸缩管径大小对破土的影响分析

当伸缩管管径发生变化时，各种土质能够破土所需要的最小进水压强见表4。从表中可以看出，当管径在0.01～0.09 m范围变化时，对于均匀松砂、均匀紧砂、一般有机黏土和压实有机黏土而言，破土所需的最小进水压强随着管径的增大而减小。

从中分析可以得到：当管径增加时，破土的推动力在增加，同时受到的阻力也在增加，如伸缩管上部土体的重力以及摩擦力都在增加，并且推动力增加程度远大于伸缩管的阻力增加的程度，所以管径越大，破土所需要的进水压强越小。

由此可知，当管径在0.01～0.09 m范围变化时，破土所需的最小进水压强随着伸缩管管径的增大而减小，当管径足够大时（超过0.09 m），破土所需的压强基本不变。

表4 不同伸缩管管径下所需最小进水压强 （单位：MPa）

5 结语

（1）本文通过理论分析与实验室模拟相结合的方式，构建了地埋式自升起喷灌装置水压作用破土过程的分析方法，推导形成了多类型土壤条件的最小进水压强公式。

（2）分析得到了无出流的灌溉设备难以破土而出的原因，通过理论计算得到无出流的灌溉设备输水压强需达到0.7 MPa才能保证在所有类型土壤中实现破土，远大于喷灌的实际工作压力。

（3）顶管顶部设计的出水口，在破土过程中起到浸润周围土体的作用，使土体结构的凝聚力减小，大幅降低了破土所需的输水压强，使得破土过程更加高效省力。在最不利条件下，如压实有机黏土，输水压强仅需达到0.15 MPa就可以顺利破土而出。

参 考 文 献：

［1］AYARS J E，PHENE C J，HUTMACHER R B，et al.Subsurface drip irrigation of row crops：a review of 15 years of research at the Water Management Research Laboratory［J］.Agr.Water Manage.，1999，42（1）：1-27.

［2］CLEMMENS A J.Measuring and improving irrigation system performance at the field level［M］.Irrigation Associa⁃tion of Australia，Melbourne.2000.

［3］MEIS C H，SIEKMEIER D A，ZIMMERER A L.Center pivot irrigation system［P］.U.S.Patent 4，011，990.

［4］VARNER J P.Irrigation system and fluid dispersion nozzle［P］.U.S.Patent 4，1977，228.

［5］李仰斌，谢崇宝，张国华，等.地埋式自动升降型一体化喷灌设备研发［J］.节水灌溉，2014（7）：75-78.

［6］李仰斌，谢崇宝，张国华，等.地埋式自动升起型取水设备研发［J］.节水灌溉，2014（6）：75-77.

［7］张国华，谢崇宝，鲁少华，等.基于钢珠驱动的全地埋式喷灌装置研发［J］.农业工程学报，2016，32（12）：102-106.

［8］ZHANG G H，XIE C B，LAI H J，et al.Buried lifting sprinkling irrigation device［J］.Journal of Irrigation and Drainage Engineering，2018，144（1）：04017058.

［9］TERZAGHI K，PECK R B，MESRI G.Soil Mechanics in Engineering Practice［M］.3rd ed.Wiley，New York，1996.

［10］FREDLUND D G，RAHARDJO H.Soil Mechanics for Unsaturated Soils［M］.Wiley，New York，1993.

［11］WHITLOW R.Basic Soil Mechanics［M］.2nd ed.Longman Scientific and Technical，Harlow，UK，1990.

［12］LAMBE T W，WHITMAN R V.Soil Mechanics SI Version［M］.Wiley，New York，2008.

［13］陈惠华.汕头市饱水细粒土黏聚力分析［J］.广州建筑，2003（6）：6-9.

［14］von BERNUTH R D，康风君.有风条件下喷射仰角对喷头性能的影响［J］.喷灌技术，1991（2）：36-40.