明渠漂浮植被水流内部能量损失和传递规律研究

槐文信，钟 娅，杨中华

（武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

1 研究背景

漂浮植被在生态河道中很常见，相比于普通的淹没植被和非淹没植被，漂浮植被漂在水面上，并不扎根于河底，植被层和底部河床之间有自由的水流区域［1］。常见的漂浮植被有浮萍科、浮叶类和睡莲水葫芦等［2］。江河湖泊中由于水体污染及富营养化，漂浮植被肆意“疯长”，对水流产生过大阻力，导致河道过水能力减小，造成缓慢流动的明渠水流［3］，而漂浮植被其本身也没有生存天敌，不会受到自然条件的阻碍，会迅速覆盖整个水面，对行洪排涝和某些水生生物繁衍产生了不利影响。但另一方面，漂浮植被为水生生物提供了好的栖息地，生态工程上广泛地应用漂浮植被净化污水［4］和富营养化的水体［5］。对漂浮植被如何适度把握、趋利避害以及化害为利成为关键，因此本文对漂浮植被水流内部能量的研究是非常有必要且有意义的。

对淹没及非淹没植被的研究目前比较广泛，比如研究带有沉水植被、坡面植被的矩形或者复式断面上流速分布和水头损失等特性［6-8］。漂浮植被对水环境的生态影响方面的研究比较成熟，但很少有学者研究明渠漂浮植被水流内部的水动力学特性。近年来一些学者利用二维［9］和三维［10］水动力模型、水流分区及混合长度理论［11］还有数值模拟［12］和实验测量［13］等方法研究漂浮植被水流的流速分布和水流结构等特性［14］。漂浮植被的顶部是自由水面，植被区水流受到的作用力主要有重力、紊动切应力和植被拖曳力，植被以下的流区除了会受到植被的影响之外，还会受到底部河床的制约，无植被的流区受力主要有重力和紊动切应力。在研究淹没植被和非淹没植被的拖曳力时，由于底部河床阻力远小于植被拖曳力，所以在底部植被区主要考虑植被拖曳力［15-16］。但在漂浮植被水流中，植被拖曳力和河床阻力都对水流有较大的影响，则淹没植被及非淹没植被水流的理论及经验方法对漂浮植被并不适用，所以很有必要研究漂浮植被对水流结构的影响。

1945年Bakhmeteff针对明渠均匀流，研究过水断面垂向上的能量分布，得出断面上能量的传递机理，分析了能量的耗散过程，并且给出了断面上能量提供、能量损失和能量传递的表达式，建立了这三者之间的关系［17］。结果表明在水流内部的任一点，当地能量提供等于能量损失和能量传递之和，整个断面能量传递总和为零。基于这个理论，明渠淹没植被水流的断面能量传递及转化也得到了分析，结果显示能量损失主要集中在植被区，能量提供亦等于能量损失和能量传递的总和［18］。本文同样基于Bakhmeteff断面能量平衡理论，力求揭示明渠漂浮植被水流的断面能量传递规律，并利用Plew［13］的水槽实验结果进行验证。

2 理论分析

2.1 水流提供能量 对图1所示的有漂浮植被的明渠恒定均匀流，根据总流能量方程可得任意两个断面之间的水头损失为hf=E1-E2，其中E1、E2为任意两个断面的总水头，因此明渠均匀流的水力坡度S=hf/∆l=(E1-E2)/∆l，其中∆l为两个断面沿水流方向的距离。均匀流中水力坡度S就是单位重量液体在单位流程内水流提供的能量，单位体积液体在单位流程内水流提供的能量为γS，其中γ为水的重度。将γS乘上流速u便得到单位体积液体单位时间内在该位置上提供的能量Wb：

W0=γSU即为断面平均的单位液体在单位时间内提供的能量，或称为断面平均的能量提供率，其中U为断面平均流速。

二维恒定均匀紊流中，沿水流方向带有植被的平均动量方程［19］为：

式中：z为垂向坐标；τ=-ρu′w′为时间平均和空间平均的雷诺切应力；ρ为水的密度；u′为纵向脉动流速；w′为垂向脉动流速；F为由植被引起的拖曳力，在植被存在的区域通常被参数化为一个关于流速u、拖曳力系数Cd和植被密度a（单位体积植被的投影面积）的二次函数［20］：

在有植被的区域，植被拖曳力由拖曳力系数、植被密度以及流速决定，然而在无植被的区域拖曳力为零。漂浮植被形态、坐标系及流速分布情况如图1中所示，其中x和z分别为纵向和垂向坐标，H为水深，hc为植被高度，hg为植被底部至河床底部的距离。

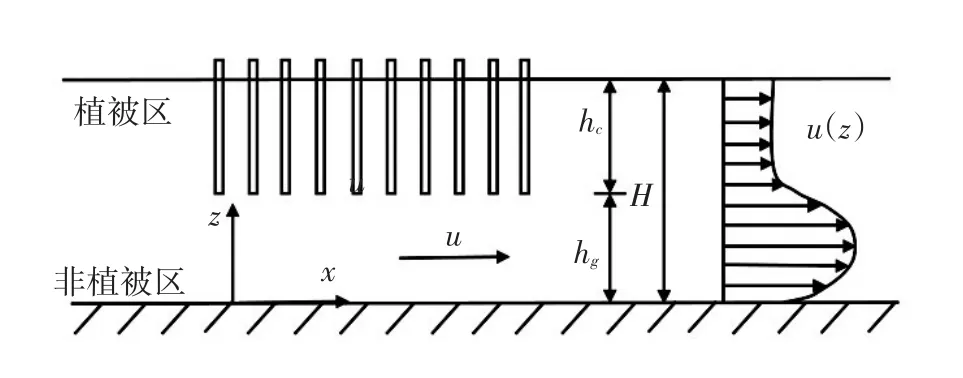
图1 有漂浮植被的明渠恒定均匀流示意图

将式（2）代入式（1）可以得到水流能量提供率：

由此可知，能量提供率由该点流速、切应力梯度和拖曳力决定。对Wb求任一点z至水面H的积分，即可得到自z至H流区内的能量提供率的累积值，亦即单位时间内该流区单位水体所提供的总能量。

从式（5）可以看出漂浮植被水流的能量提供累积值与无植被水流情况下是一致的，则表示从水底到水面整个流区的总能量提供。

2.2 水流损失能量 明渠漂浮植被水流中的能量损失大致分为两部分：（1）水体由于切应力梯度的存在会产生变形，水体克服水流阻力损失的能量；（2）水体克服植被拖曳力损失的能量。如图2所示，水体在切应力梯度的作用下产生变形，变形时顶面切应力相对底面做的功即为阻力功，忽略高阶微量后可得由水流阻力造成的能量损失率［17］为：

图2 水体在切应力梯度作用下的变形

由植被拖曳力造成的能量损失率可定义为单位时间间隔单位水体内植被拖曳力所做的功为：

有植被的流区植被拖曳力造成的能量损失率为uF，无植被流区则为零。由式（6）和式（7）可求得能量损失率为：

对Ws求任一点z至水面H的积分，即可得到自z至H流区内的能量损失率的累积值，亦即单位时间内该流区单位水体所损失的总能量：

将式（2）沿z至H积分可得：

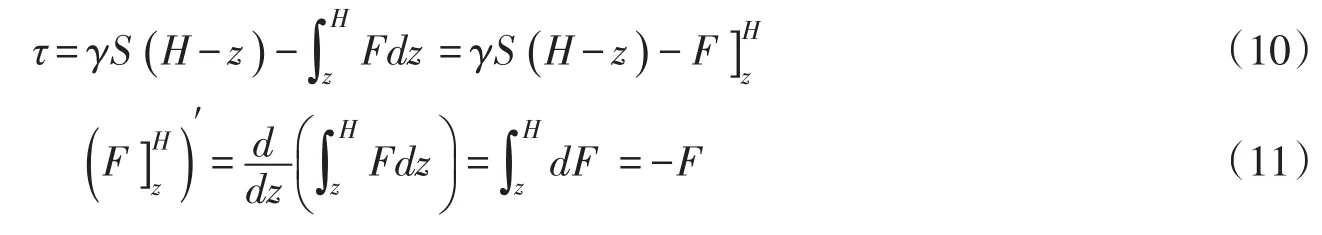
将式（10）和式（11）代入到式（9）得到植被水流中由水流自身涡黏性引起的能量损失为：

其中：

式（12）中等式右边第一项是无植被水流中的总能量损失，第二项是由于植被的存在约束了水流紊动从而减小能量损失。植被本身与水流交互运动又会增加水流的紊动，所以由植被引起的能量损失为：

总的能量损失为：

或者：

当z=0时，u=0，从水底到水面整个流区的总能量损失

2.3 水流传递能量 为了保证水流内部的能量平衡，主流区多余的能量会向河底区和植被流区传送。如图3所示，微小水体A在单位时间内对其下水体所做的功为(τdxdy)u，同时接受其上水体对其做功为忽略高阶微量后微小水体A向河底方向传送的能量（简称能量传递率），即单位水体在单位时间内向河底方向传送的能量为：

图3 水体与其上下水体相对关系

对Wt求任一点z至水面H的积分，即可得到自z至H流区内的能量传递率的累积值，亦即单位时间内该流区单位水体自该流区向边界方向传递的总能量：

式（17）中等式右边第一项是无植被水流中的总能量传递，第二项代表的是漂浮植被水流中植被的存在消耗大量的能量，使得能量不断地向植被顶端传递。

当z=0时，u=0，从水底到水面整个流区的总能量传递

3 水流内部能量平衡

3.1 点能量平衡 由式（16）有：

则：

此式即为漂浮植被恒定均匀流中点的能量平衡关系式，与无植被二元明渠均匀流的形式一致且结论相同，表明漂浮植被水流内部任一点的能量提供率等于能量损失率与能量传递率之和。

本文使用Plew的实验室水槽试验结果Run B13来验证漂浮植被明渠流的能量平衡情况。本研究中植被效应在垂向流速和切应力分布上占主导地位，且鉴于Plew的实验测量中选取水槽中心断面作为测量断面，因此水槽边壁对流动结构的影响较小。Run B13中各参数情况为：水深H=0.2 m，水槽宽度B=0.05 m，植被高度hc=0.1 m，植被密度a=1.272 m-1，水力坡度S=0.156‰，水深平均流速U=0.0848 m/s，拖曳力系数Cd=1.07。水槽实验测得的沿水深流速分布如图4所示，可以看出植被区的流速明显小于非植被区。

图4 水槽试验沿水深流速分布

图5 能量提供率、能量损失率和能量传递率分布

根据本文的理论分析，得到漂浮植被恒定均匀流中的能量提供、能量损失和能量输移情况如图5所示，所有结果都用断面平均能量提供率W0进行了无量纲化。

从图5可以看出：（1）式（1）是物理意义上定义的断面能量提供率，式（4）是作者推导出的由切应力、流速和植被拖曳力表达的能量提供率。由于植被区与非植被区的过渡区植被扰动和水流强烈紊动作用，另外试验也存在测量误差，使得水深方向上并不是每个测点的两种能量提供率都能完全吻合，部分测点存在一定的偏差，尤其在交界面附近更为明显。但总体来说能量提供率大致等于能量损失率和能量传递率之和，符合漂浮植被均匀流中点的能量平衡规律；（2）无植被流区的能量损失传递规律与一般明渠流相似，能量提供率总是大于能量损失率，差异在于无植被流区多余的能量累积起来除了向近壁流区传输，更多的是向植被流区补充以达到整个流区的能量平衡；（3）植被流区的能量分布情况与无植被流区相比差异较大，植被的存在导致了较大的附加的能量损失，越靠近植被底部能量损失越大，在植被流区和无植被流区的交界处能量损失达到最大，越过植被进入无植被流区后能量损失骤减至较小值；（4）植被流区的能量传递率为负值，能量损失率总是大于能量提供率，说明无植被流区不断地向植被流区补充能量；（5）在近壁流区时均流速梯度和切应力都较大，最易形成涡体增加能量损失，但远小于植被流区的能量损失。说明均匀流中整个流区所提供的全部能量与整个流区的总能量损失相等。这个结论既适用于层流，也适用于紊流的时均流动，即公式中的水流运动要素均指时均值而言。

由式（5）、式（14）和式（16）得出：

3.2 面能量平衡 由理论分析得出，当z=0时，

或者

说明任意水深处至水面的总的能量提供等于总的能量损失和总的能量传递之和。为了更好地进行能量平衡关系分析，式（21）中的各项都用断面平均的整个流区总能量提供进行无量纲化，使用Plew的实验室水槽试验结果Run B13得到的各能量累积曲线如图6所示。

由图6可以看出，从水面至河底，能量提供曲线逐渐平稳增加，在河底达到最大值；能量传递累积曲线在植被区为负值，在植被区和非植被区的交界处达到最小值，然后逐渐增加为正值，在河床底部主流区和近壁流区的交界处达到最大值，最后逐渐减小，在河床底部为零；能量损失曲线在植被区快速增长，在非植被区增长较缓，最后在河床底部交于能量提供曲线。可以看出断面中植被区的能量损失较大，其他流区的能量不断地向植被区传递，从水面至约0.15H水深处，能量传递累积均为负值，说明在这段流区内能量损失大，能量总提供小于能量总损失。断面总的能量传递为零，总的能量提供与总的能量损失相等。从能量损失可以看出，植被引起的能量损失比水体自身的能量损失要大得多。由植被引起的能量损失主要分布在植被区，非植被区为零。图中能量传递和能量损失的和大致等于能量提供，由植被引起的能量损失与由水体自身引起的能量损失之和大致等于总的能量损失，说明面能量的平衡规律和点能量的平衡规律一致。

图6 断面能量提供、能量损失和能量传递累积曲线

图7 紊流功能损耗累积曲线

4 水流能量损失过程

Bakhmeteff根据天然河流实测资料给出了垂向上断面能量累积曲线，其中能量传递累积曲线有个极大值点。这一点把水流分成两个区，以上为主流区，以下为近壁流区，并且近壁流区的高度约为水深的10%，河流的主流区提供的能量约为全部能量的90%，断面中约90%的能量传递到近壁流区损失掉，只有小部分在主流区就地损失。由此可见，近壁流区在水流能量损失方面占有特别重要的地位。而在本文的漂浮植被水流中，植被的存在使主流区分成了植被区和非植被区，近壁流区的高度约为水深的2%（见图7），植被区的能量损失远大于非植被区和近壁流区，约75%的能量损失在植被区，约10%的能量损失在非植被区，约15%的能量损失在近壁流区。

对明渠漂浮植被水流而言，除了考虑紊流的时均流动规律之外，还必须进一步补充考虑紊流的紊动性质，即涡体的产生、运行、震荡、分裂、消亡的过程，以及涡体本身还具有的紊动动能。紊动由于脉动具有的紊动动能为：

它来源于水流的时均能量，但是一旦转化为紊动动能之后，就不可能重新转化为时均能量，而只能逐步在涡体的运行、震荡、分裂的过程中，通过液体的黏性作用转化为热能。在河床底部附近由于时均流速梯度和切应力都比较大，加之底部粗糙度的干扰，故在底部附近最易形成涡体，这些涡体将上升到主流区，由于不稳定导致脱落转化为热能而散失。这些涡体的紊动动能只能来源于近壁流区的的水流时均能量，也就是说，从主流区传递到近壁流区的能量，有一大部分会转化为紊动动能。

自z至H流区内的紊动动能的累积值如图7所示。在近壁流区附近，紊动动能累积值与能量传递累积值几乎相等，说明近壁流区内的绝大部分能量转化为紊动动能，非常小的一部分因抵抗近壁流区中的阻力而在该区内转化为热能损耗掉。

5 结论

本文基于Bakhmeteff的过流断面能量平衡理论，推导出了漂浮植被水流断面的能量提供、能量损失和能量传递的表达式，以及断面上3种能量累积的表达式，采用Plew的水槽实验数据得出了漂浮植被水流断面上能量提供、能量损失和能量传递的分布规律和能量累积曲线。通过分析3种能量的变化规律和漂浮植被对水流的影响可得到以下结论：

（1）对于漂浮植被水流中的任意一点，能量提供率等于能量损失率与能量传递率之和；从任意水深处至水面的水流区域内，总的能量提供等于总的能量损失和总的能量传递之和。整个断面上的能量传递累积值为零，说明整个断面上的能量提供等于能量损失，这一结论与无植被的明渠流一致。

（2）能量损失集中在植被区，在植被区与非植被区的交界处（植被底部）损失达到最大，植被区内的动量交换和能量交换更加强烈。漂浮植被水流中，植被会限制水流本身的紊动，但也会对水流造成扰动。

（3）和明渠流能量分布规律不同的是，漂浮植被水流中大部分区域（特别是植被区）断面的能量损失大于能量提供，能量传递为负，这说明中间流区的水流能量在不断地运输到植被区和河床底部，可以看出植被区的能量消耗比河床底部大很多。

（4）河床底部近壁流区内的绝大部分能量转化为紊动动能，非常小的一部分因抵抗近壁流区中的阻力而在该区内转化为热能损耗掉。

参 考 文 献：

［1］PLEW D，SPIGEL R，STEVENS C，et al.Stratified flow interactions with a suspended canopy［J］.Environmen⁃tal Fluid Mechanics，2006（6）：519-539.

［2］ROSMAN J，KOSEFF J，MONISMITH S，et al.A field investigation into the effects of a kelp forest（Macrocystis pyrifera）on coastal hydrodynamics and transport［J］.Journal of Geophysical Research，2007（112）：C02016.

［3］PLEW D，STEVENS C，SPIGEL R，et al.Hydrodynamic implications of large offshore mussel farms［J］.IEEE Journal of Oceanic Engineering，2005，30（1）：95-108.

［4］李寒娥，李秉滔，黄耀丽，等.漂浮植物净化污水试验研究［J］.水处理技术，2006，32（8）：46-49.

［5］娄敏，廖柏寒，刘红玉，等.3种水生漂浮植物处理富营养化水体的研究［J］.中国生态农业学报，2005，13（3）：194-195.

［6］王协康，刘同宦，叶龙，等.坡面柔性植被阻水效应及其局部水头损失特性试验研究［J］.四川大学学报（工程科学版），2013，45（2）：22-27.

［7］王文雍，刘昭伟，陈永灿，等.刚性沉水植被水流的流速垂向分布［J］.四川大学学报（工程科学版），2012，44（S2）：253-257.

［8］刘超，杨克君，刘兴年，等.植被作用下的弯曲复式河槽漫滩水流二维解析解［J］.四川大学学报（工程科学版），2012，44（6）：7-12.

［9］ZHAO F，HUAI W，LI D.Numerical modeling of open channel flow with suspended canopy［J］.Advances in Water Resources，2017（105）：132-143.

［10］O'DONNCHA F，HARTNETT M，PLEW D.Parameterizing suspended canopy effects in a three-dimensional hy⁃drodynamic model［J］.Journal of Hydraulic Research，2015，53（6）：714-727.

［11］HUAI W，HU Y，ZENG Y，et al.Velocity distribution for open channel flows with suspended vegetation［J］.Ad⁃vances in Water Resources，2012，49（8）：56-61.

［12］CHEN Z，JIANG C，NEPF H.Flow adjustment at the leading edge of a submerged aquatic canopy［J］.Water Re⁃sources Research，2013，49（9）：5537-5551.

［13］PLEW D.A depth-averaged drag coefficient for modelling flow through suspended canopies［J］.Journal of Hy⁃draulic Engineering，2011，137（2）：234-247.

［14］TSEUNG H，KIKKERT G.Three-Dimensional flow behaviour generated by suspended canopy［C］//Proceedings of the 7th International Conference on Asian and Pacific Coasts（APAC 2013）Bali，Indonesia，2013：24-26.

［15］CAROLLO F，FERRO V，TERMINI D.Flow resistance law in channels with flexible submerged vegetation［J］.Journal of Hydraulic Engineering，2005，131（7）：554-564.

［16］LEE J，ROIG L，JENTER H，et al.Drag coefficients for modeling flow through emergent vegetation in the Flori⁃da Everglades［J］.Ecological Engineering，2004（22）：237-248.

［17］BAKHMETEFF B，ALLAN W.The mechanism of energy loss in fluid friction［J］.Transactions of the American Society of Civil Engineers，1946，111（1）：1043-1102.

［18］HUAI W，HAN J，GENG C，et al.The mechanism of energy loss and transition in a flow with submerged vegeta⁃tion［J］.Advances in Water Resources，2010，33（6）：635-639.

［19］NIKORA V，GORING D，GRIFFITHS G.Spatially averaged open-channel flow over rough bed［J］.Journal of Hydraulic Engineering，2001，127（2）：123-133.

［20］LIGHTBODY A，NEPF H.Prediction of velocity profiles and longitudinal dispersion in emergent salt marsh vege⁃tation［J］.Limnology and Oceanography，2006，51（1）：218-228.