一种基于前馈定时的OQPSK解调方法

张丽娜，陈敬乔

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

偏移正交相移键控(Offset Quadrature Phase Shift Keying，OQPSK)是一种改进的正交相移键控(Quadrature Phase Shift Keying，QPSK)，与QPSK调制信号相比，OQPSK信号同相支路码元与正交支路码元在时间上偏移了半个符号周期。OQPSK调制除了具有QPSK 调制的所有优点外，还消除了相邻符号间的180°相位跳变现象[1]，在带宽受限的通信系统中，OQPSK信号包络起伏小，经过非线性功率放大器后不产生明显的功率谱旁瓣增生效应。因此，OQPSK调制所具有的恒包络特性、良好的频谱效率及功率效率使得它广泛地应用于卫星通信中。

典型的OQPSK解调[2]是常用的基于反馈定时的解调方法，采用Gardner算法[3]提取误差，调整AD时钟或者后端重采样[4-5]时钟，由于定时和载波恢复同时进行，二者相互制约，环路参数调试难度比较大，特别是低信噪比的情况下，实现比较困难，针对此问题，本文提出一种基于前馈定时的解调方法，将定时和载波恢复分开进行，解决了环套环调试困难的问题，并对解调流程和关键算法进行了详细分析，最后对仿真结果和工程实践进行了比较。

1 OQPSK 调制基本原理

OQPSK调制实现框图如图1所示。

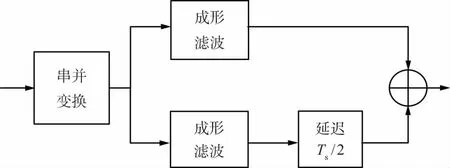
图1 OQPSK调制实现框图

OQPSK调制也是把输入数据流分成同相与正交2个数据流，它们的相位关系与 QPSK 相同，QPSK调制的信号经过成形滤波[6]，其中一路有半个符号的延时滞后送给基带采样D/A，完成OQPSK调制。

2 OQPSK解调基本原理

OQPSK信号的解调同QPSK解调原理基本相同，因为在调制时Q支路信号在时间上延迟了半个周期，所以在解调端的Q支路上也应该延时半个符号再进行抽样判决，从而保证对2个支路能进行正确的采样，然后经过并/串变换来恢复原始信号[7]。

OQPSK解调常用的基于反馈定时的解调方法，其解调框图如图2所示。

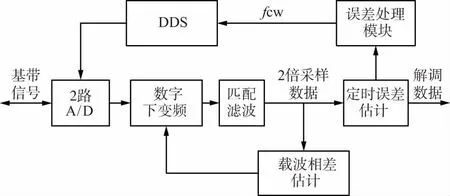
图2 基于反馈定时的解调框图

该解调方法是将定时估计误差反馈给DDS，用于调整AD采样时钟来完成定时，A/D采样的数据经过数字下变频、匹配滤波之后进行载波恢复，用于载波恢复的数据同时送给定时误差估计模块，定时后的数据送给后续处理。此解调方案的缺点是在载波未同步的情况下，符号同步非常困难，同时载波同步又需要符号同步提供正确的时钟信息[8-9]，定时环路延时大，信噪比较低时程序参数调试困难。

3 基于前馈定时的解调方案

鉴于传统的基于反馈定时的解调方法中调试复杂问题，提出了一种新的解调方案，即基于前馈定时的解调方法，实现如图3所示。

解调中摆脱环套环的形式，将载波恢复和符号定时恢复分开来做，先进行载波恢复，再完成符号定时。符号定时用基于频域非线性估计算法提取定时误差信息，用误差控制数据内插的方式实现符号定时调整，载波恢复先用FFT进行载波频差估计，再用costas环实现残余载波恢复。

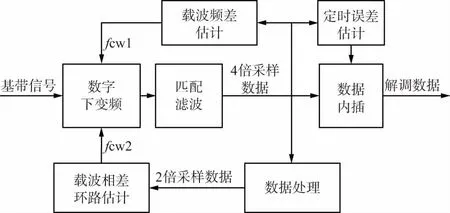
图3 基于前馈定时的解调框图

3.1 定时恢复

定时恢复用基于频域非线性估计算法的内插定时，匹配滤波后的4倍采样数据采用Q路和延迟半个符号后的I路利用加窗的平方环算法进行定时误差估计，差值滤波器利用处理后的定时误差处理作为误差进行数据内插从而完成定时。

当载波频偏较小时，匹配滤波后的信号[10]可近似表示为：

r(t)=As(t-τ)ej(Δωt+θ)+n(t)。

(1)

对匹配滤波后的复基带信号进行采样，得到

rk=r(kT/N)=Ask+nk，

(2)

式中，N=4。通过计算y(t)=r(t)r*(t)的傅里叶换Y(f)在f=1/T处的相位来获得符号定时误差的估计，估计结果[11-13]为：

(3)

(4)

L为观测符号数。

由于OQPSK调制的原因，进行定时误差估计[14-15]的数据需要将延迟的半个符号的数据还原回来再进行估计，导致I、Q两路信号的频偏不同，所以该定时估计算法对频偏要求极高，需要在几乎无频偏的情况下才能实现准确估计，这就需要在定时前实现载波的精确恢复。

下面对算法性能进行仿真，假定OQPSK调制，归一化定时偏差1/16，仿真次数1 000，估计长度1 024，仿真结果如图4所示，可知在归一化频偏6Rs/100 000时，归一化定时估计误差小于0.06。

图4 定时估计性能仿真

利用此条件仿真不同符号信噪比下误差的估计方差，仿真结果如图5所示，可以将归一化定时估计的方差[4-5]控制小于0.000 3范围内，如果不考虑内插器本身引入的误差，定时恢复后解调性能的恶化小于0.1 dB。

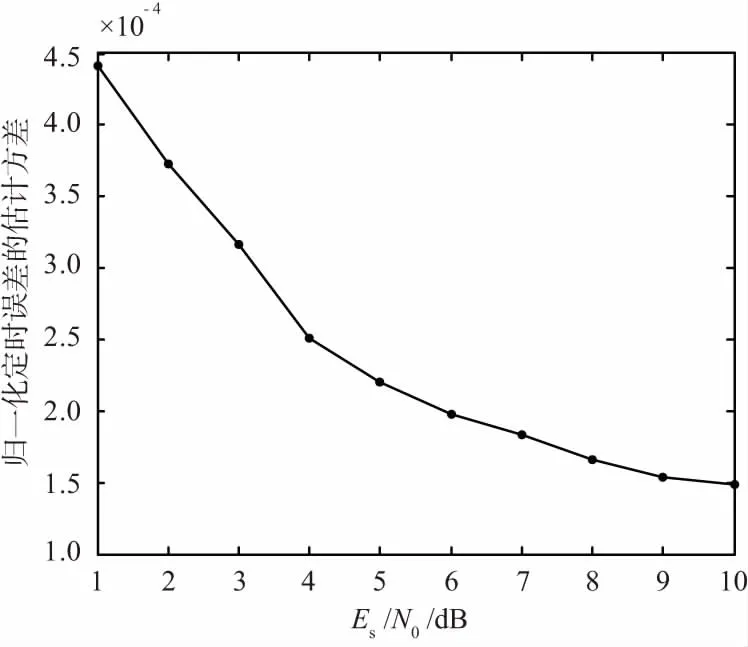
图5 OQPSK的定时估计算法性能

3.2 载波恢复

3.2.1 载波频率估计

载波频率估计利用FFT实现[16-17]。FFT是对载波频率进行了有限精度的量化，量化精度与FFT的点数相关。算法描述如下：匹配滤波之后的4倍采样样本为rk，通过下述运算消除调制数据的影响：

(5)

式中，φk=arg[rk]；ρk=abs(rk)；M为与调制方式有关的常数，对于OQPSK，M=4；d为设计参数，一般取0≤d≤M。

下面对算法的性能进行仿真，仿真条件：OQPSK调制，归一化载波频差为1/32，Es/N0=0 dB，匹配滤波之后的数据是4倍采样，理想高斯信道下的仿真结果如图6所示。

由仿真结果可知，可以准确地估计载波频率FFT点数是8 192。由于FFT的点数为8 192，输入4倍采样数据进行了4次方的处理，因此FFT估计精度为1/8 192符号率。

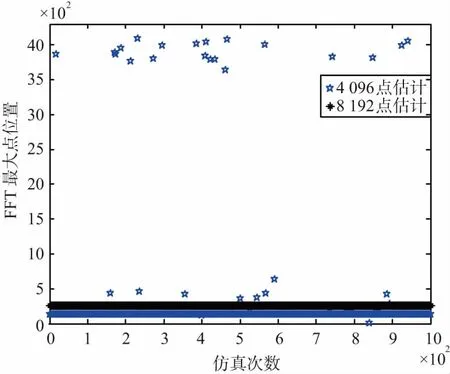
图6 FFT载波频率估计的性能

3.2.2 载波相位估计

载波相位估计采用Costas环，主要由鉴相器和环路滤波器组成。鉴相器利用数字下变频后的2倍采样数据产生相位误差信号，经过环路滤波后，送入数字下变频模块产生本地载波，完成本地载波恢复[18-19]。其中，鉴相函数为：

e(k)= sign(I(k))Q(k)-

(6)

对上述载波恢复算法的性能进行仿真，假定OQPSK调制方式，归一化频偏Rs/4 096，不考虑定时偏差，仿真数据个数20 000。对载波恢复后的数据进行误比特率统计，仿真结果如图7所示，在Es/N0小于7时解调性能恶化小于0.5 dB。

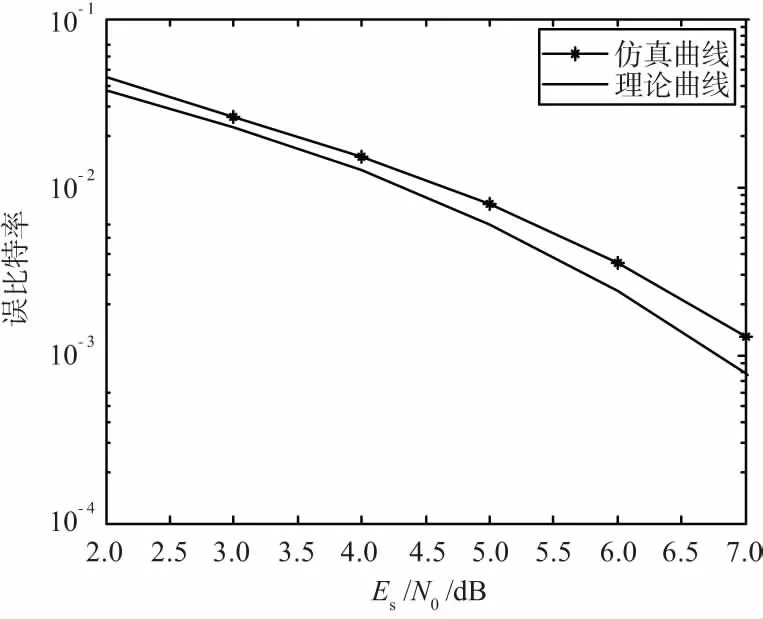
图7 载波相位估计性能仿真

3.3 实现验证

采用前馈定时的解调方案在FPGA平台上实现OQPSK的中频环调制解调验证，采用不同的编码方式，性能测试结果如表1所示。由表1可知，不同编码方式下，中频环解调信噪比恶化值小于0.7 dB，考虑中频等其他恶化0.2 dB，可得由解调导致的信噪比恶化小于0.5 dB，与仿真相符。

表1 OQPSK解调性能测试结果

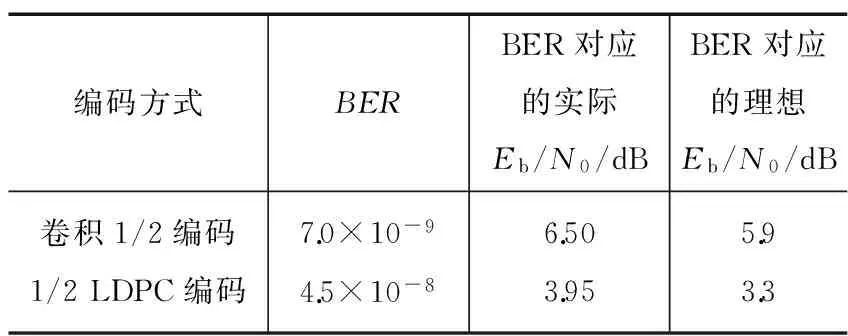
编码方式BERBER对应的实际Eb/N0/dBBER对应的理想Eb/N0/dB卷积1/2编码1/2LDPC编码7.0×10-94.5×10-86.503.955.93.3

4 结束语

在典型的OQPSK解调方法基础上提出了一种基于前馈定时的OQPSK解调方案，仿真了载波恢复和定时恢复对解调性能的影响，得出定时估计需要在归一化频偏很小的情况下才能准确估计，实验证明，归一化频偏小于6Rs/100 000时，定时恢复导致的性能恶化小于0.1 dB，通过合理的参数设计可以将OQPSK解调导致的性能恶化控制在小于0.5 dB范围内，仿真的相关参数可以作为设计实现的参考。

[1] 赵清华.OQPSK调制解调的性能研究[D].重庆：重庆大学，2010：19-39.

[2] 韩星，张华冲，熊志广，等.全数字高速OQPSK信号解调技术分析[J].无线电工程，2011，41(12)：18-20.

[3] 李建海，成亚勇.QPSK调制解调中的Gardner定时恢复算法研究与性能分析[J].无线电工程，2004，34(10)：55-56.

[4] 张丽娜.数字重采样误差对解调性能的影响[J].无线电工程，2011，41(2)：19-20.

[5] 陈敬乔.非相干重采样技术及应用[J].信息通信，2014(2)：8-9.

[6] 丁龙刚，马虹.卫星通信技术[M].北京：机械工业出版社，2006.

[7] 童莹，陈瑞.通信原理中的QPSK和OQPSK的仿真与分析[J].江苏科技信息，2013(6)：51-53.

[8] 胡宵.OQPSK信号同步算法在IEEE802_15_4通信中的应用[D].西安：西安电子科技大学，2004：9-22.

[9] 苏耀峰，杨谨.基于VHDL语言的OQPSK解调器设计与实现[J].Moden Computer，2009(6)：175-177.

[10] 潘申富.一种低信噪比解调的实现方案及性能仿真[J].无线电通信技术，2011，37(2)：55-57.

[11] 陈振骐.OQPSK盲接收的信号同步与解调算法研究[D].北京：清华大学，2003：48-51.

[12] 位小记，谢红，郭慧.基于瞬时特征参数的数字调制识别算法[J].传感器与微系统，2011，30(1)：127-130.

[13] 余嘉，陈印.基于BP神经网络的数字调制识别方法[J].传感器与微系统，2012，31(5)：16-19.

[14] GARDNER F M.Interpolation in Digital Modems.I：Fundamentals[J].IEEE Transactions on Communications，1993，41(3)：501-507.

[15] OERDER M，MEYR H.Digital Filter and Square Timing Recovery[J].IEEE Trans.on Communications，1998，36(5)：605-612.

[16] 杨振国，杨鸿文，郭文彬.卫星通信系统与技术[M].北京：北京邮电大学出版社，2003.

[17] 杨亚龙，嵩天，朱洪辰.高效命名数据网卫星视频直播方法[J].计算机科学与探索，2018，12(1)：17-28.

[18] 赵潜.通信系统中的全数字载波恢复技术研究及实现[D].西安：西安电子科技大学，2012：15-20.

[19] 袁山洞，刘衡竹，陈旭灿，等.低复杂度自适应单载波频域均衡器的FPGA实现[J].计算机科学与探索，2016，10(8)：1072-1079.