无定型碳的微波损耗特征及其耦合热转换影响因素分析

鲁艳飞，宋勃震，张 锐,，蔡林杰，张瑜萍，董陈江

1 郑州航空工业管理学院，郑州450046

2 郑州大学 材料科学与工程学院，郑州450001

SiC晶体是一种最重要的半导体材料，具有较高的电阻率、较好的热稳定性、良好的机械强度和硬度、可调电导率和低密度等优点[1-5]。工业 SiC一般是通过 Acheson法合成[6]，合成温度高达2200°C ～ 2400°C，既浪费能量，又污染环境[7]。因此急需寻求一种简易、经济、环保的方法合成SiC。

作为一种新型的加热方式，微波加热在高温材料制造领域得到了广泛的关注[8-10]。微波加热过程中的体能量吸收方式使得材料整体均匀升温，克服了传统加热方式产生的温度梯度。微波在材料内部的损耗是微波加热的基础，微波损耗特征决定了材料的热生成过程，进而影响化学反应进程。因此，通过此控制实验条件降低SiC合成温度[11]，即可采用微波加热方法合成出SiC粉体[12]、SiC晶须[13]和SiC纳米棒[14]等。由于微波加热的复杂性[15-17]，微波损耗的理论计算和微波加热过程中的温度测量通常不易进行。因此，本文将运用多物理场仿真软件COMSOL对微波加热无定形碳的动态过程进行模拟分析，通过分析微波损耗特征及其所导致的温度变化规律对SiC合成过程中的热效应问题做出解释，以期完善微波加热理论、优化生产工艺。

1 微波-热耦合控制方程

微波在真空中的传播基于Maxwell方程组：

对于存在极化损耗和磁化损耗的介质，电容率和磁导率为复数，即

根据时谐场中存在线性介质的Poynting定理可得各种损耗功率密度和电磁能量密度的瞬时值[18]：

其中式 (5) 中的PE包括：

即：ajEPPP += (其中，σ 为电导率，K为非电性场强度)。

进一步可以得到各种损耗功率密度和电磁能量密度的平均值[18]：

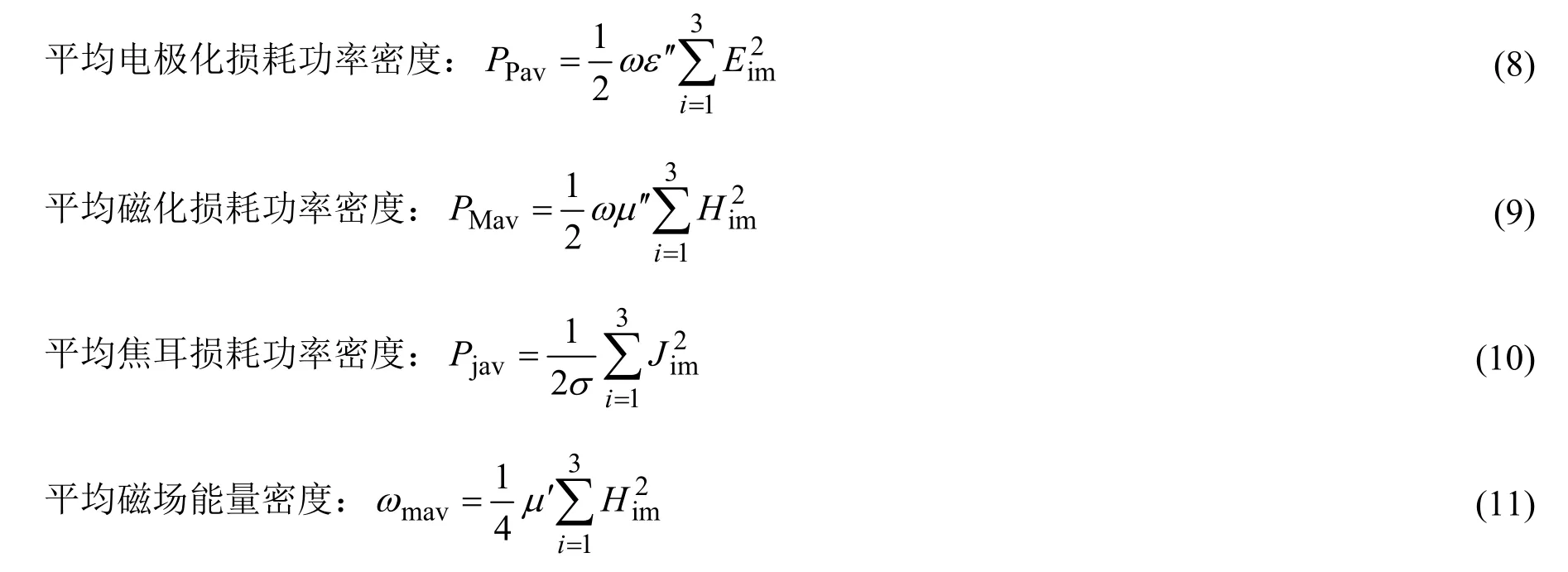
忽略微波的磁效应，碳的微波损耗包括电极化损耗 (介电损耗) 和焦耳损耗 (电导损耗)。

电流密度与电场的关系为

联立式 (8)、(10) 和 (12) 可得平均电损耗功率密度：

由Maxwell方程组可以推导出损耗角正切与介电常数虚部和电导率的关系为

联立式 (13) 和 (14) 可得平均电损耗功率密度：

微波在谐振腔中传播遵从电磁波频域方程：

边界条件为：

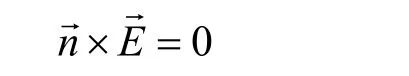
电磁波在材料内部有一定的穿透深度，用集肤深度表示：

固体传热方程为

边界条件为

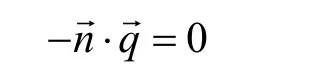
对于微波加热只存在电磁损耗，式 (18) 变为：

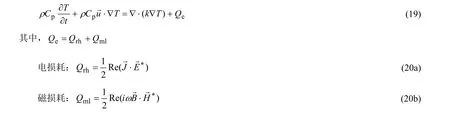
边界电磁热源为

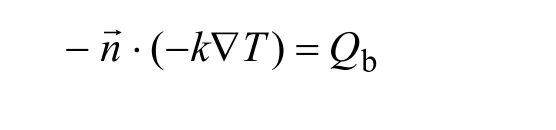
图1 微波加热模型Figure1 Microwave heating model

2 微波加热碳的动态过程模拟

2.1 建模及参数设置

运用COMSOL建立的微波加热模型如图1所示：长方体加热腔尺寸为0.1092 m × 0.0546 m× 0.222 m，BJ-26波导口尺寸为 0.1092 m ×0.0546 m，位于长方体加热腔的XY面上，波导口激励频率为2.45 GHz，输入功率为10000 W，工作模式为 TE103，圆柱形碳半径和高度均为0.006 m，中心点坐标为 (0.0546 m，0.0273 m, 0.111 m)。

微波加热腔壁为完美导电体，全反射微波，腔内为真空，不参与传热。模拟分析采用的真空电磁参数为：相对介电常数1，相对磁导率1，电导率0。

表1给出了对东胜褐煤进行元素分析所得到的结果。可以看出，东胜褐煤成分以碳为主，因此本文采用东胜褐煤的性能作为模拟分析中无定形碳的参考值。

表2 东胜褐煤元素分析结果Table2 Element analysis results of Dongsheng lignite

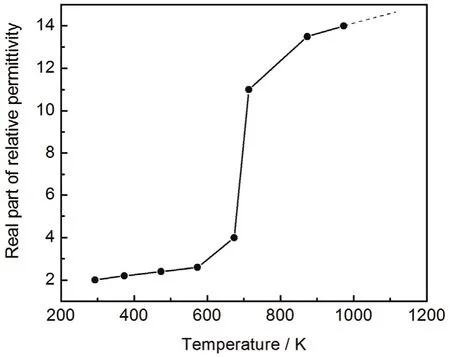
图2 相对介电常数实部随温度的变化Figure2 Variation of the real part of relative permittivity with temperature

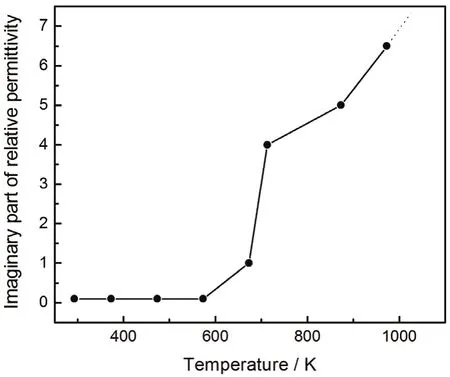
图3 相对介电常数实部随温度的变化Figure3 Variation of the imaginary part of relative permittivity with temperature

碳的相对介电常数实部和虚部在20°C ～ 700°C范围内为阶段线性变化，外延部分也设为线性变化，碳的相对介电常数实部和虚部与温度的变化关系分别如图2和图3所示。电导率与温度的变化关系可以近似用公式 (21) 表示：

式中，σ0为温度t0时的电导率 (S/m)，α 为电阻温度系数 (°C-1)。

根据文献 [20]，微波频率为 2.45 GHz时碳的室温电导率约为 0.02 S/m，电阻温度系数设为-0.0005°C-1，可以将碳的电导率随温度的变化关系写成：

碳的恒压热容为502 J/(kg·K)，材料库中碳的导热系数和密度都是温度的函数。

2.2 模拟结果分析

2.2.1 温度变化过程及微波损耗特征

微波加热前6 s碳的温度变化如图4所示。微波加热过程中，碳外表面一点 (0.0546 m，0.0273 m，0.105 m) 过中心点 (0.0546 m，0.0243 m，0.111 m) 到另一点 (0.0546 m，0.0273 m，0.117 m) 的温度梯度随弧长的变化如图5所示。可以看出，碳是整体同时升温，从外到内碳的温度逐渐减小，说明升温速率从外到内逐渐降低。0 s ～ 5 s区间内，内外温差逐渐拉大；随着热传递的进行，5 s ～ 6 s期间，温差开始缩小，对应碳中心点温度梯度在5 s时开始减小，如图6所示。

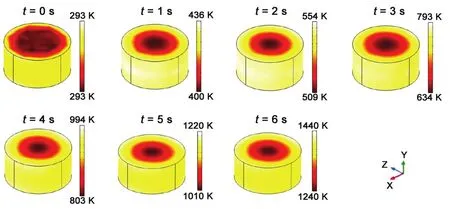
图4 微波加热碳的温度变化过程Figure4 Temperature change process during the microwave heating of carbon

图5 温度随弧长的变化Figure5 Variation of temperature with arc length

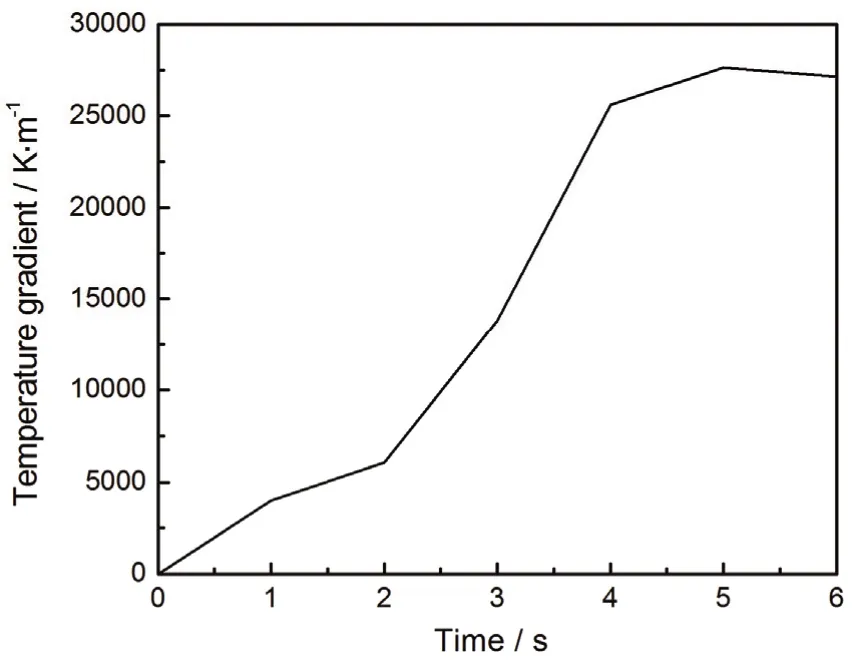
图6 中心点温度梯度随时间的变化Figure6 Variation of center point temperature gradient with time

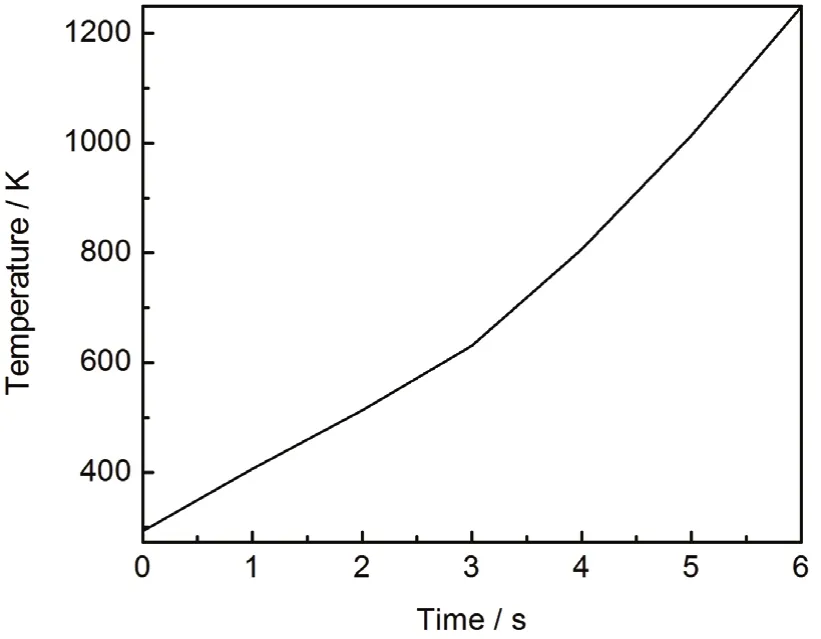
图7 中心点温度随时间的变化Figure7 Variation of center point temperature with time

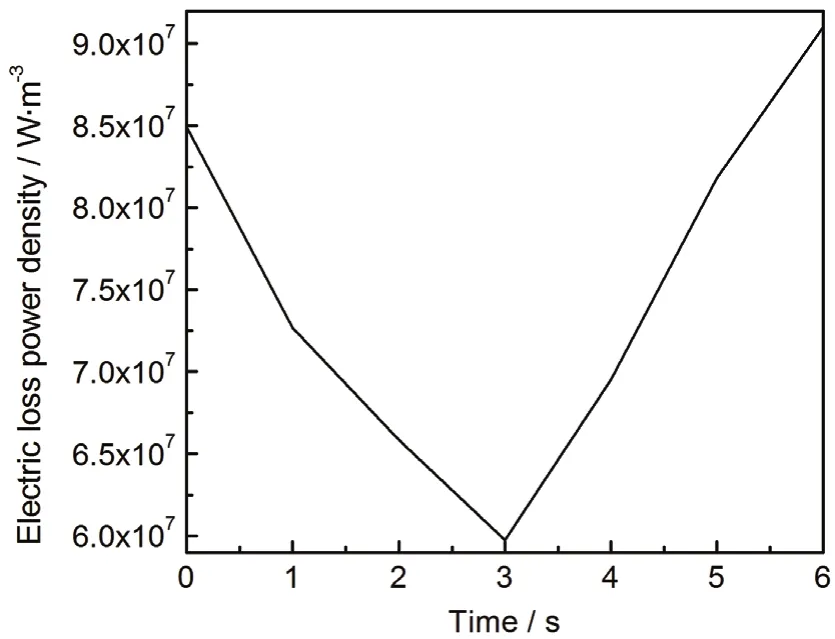
图8 中心点电损耗功率密度随时间的变化Figure8 Variation of center point electric loss power density with time

中心点温度随时间的变化关系如图7所示：0 s ～ 3 s升温速率逐渐降低，3 s ～ 6 s升温速率逐渐升高。这主要是由于0 s ～ 3 s之间电损耗减小，而3 s ～ 6 s之间电损耗增大 (如图8所示)，也就是说升温速率随电损耗的增大而升高。

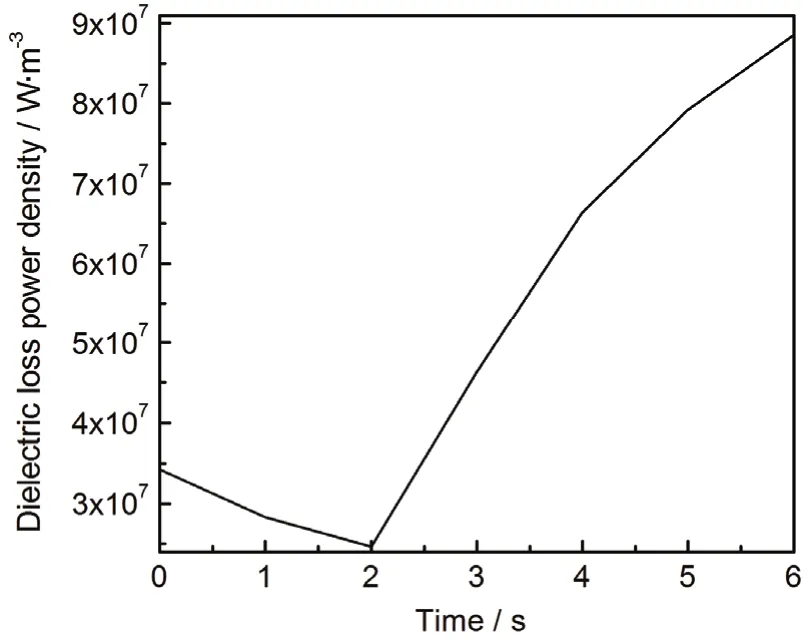
图9 中心点介电损耗功率密度随时间的变化Figure9 Variation of center point dielectric loss power density with time

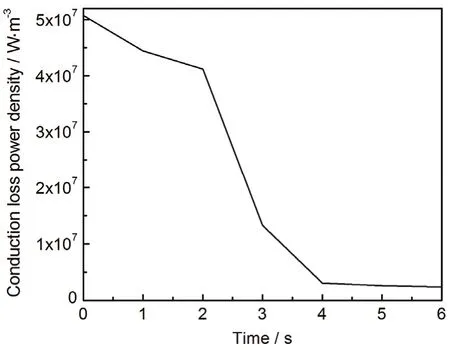
图10 中心点电导损耗功率密度随时间的变化Figure10 Variation of center point conduction loss power density with time

2.2.2 介电损耗与电导损耗的变化特征

电损耗功率密度主要包括介电损耗功率密度和电导损耗功率密度，其随时间的变化关系分别如图9和图10所示。

图11是中心点电场模随时间的变化关系曲线。根据式 (17)，微波在材料内部有一定的穿透深度，随着复介电常数和电导率的增大，穿透深度减小，相应的中心点电场模也减小。根据公式，微波损耗与电场模平方成正比，电场减小导致微波损耗减小。图10中电导损耗与电场模减小趋势大致相同，而图9中介电损耗在0 s ～ 2 s之间减小，2 s ～ 6 s之间增大，3 s时与电损耗同时增大，说明微波加热碳的过程中，0 s ～ 2 s之间介电损耗和电导损耗共同主导，2 s之后介电损耗占主导。

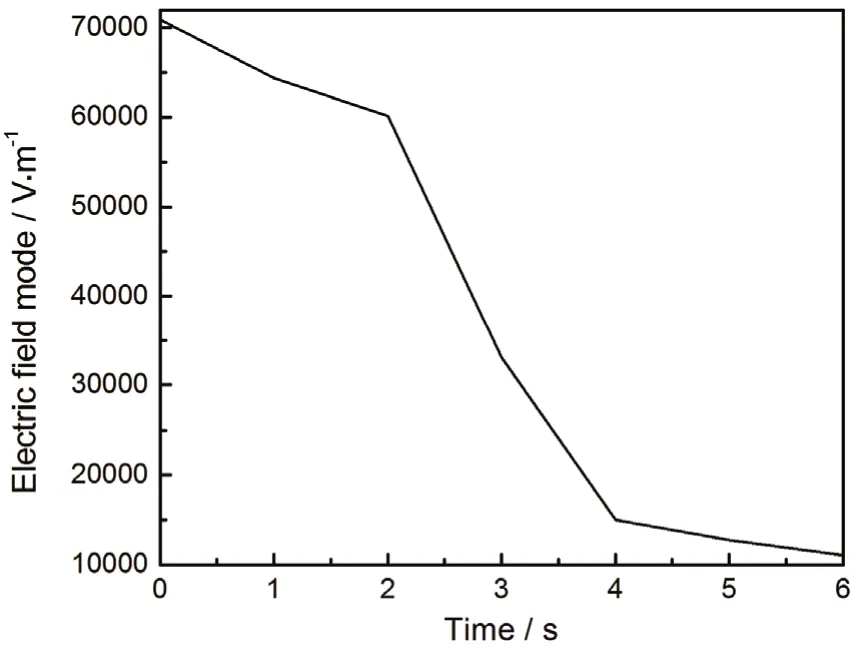
图11 中心点电场模随时间的变化Figure11 Variation of center point electric field mode with time

3 微波热效应的影响因素

3.1 复介电常数的影响

分别讨论相对介电常数实部和虚部对耦合热的影响：(1) 控制相对介电常数虚部为 0.1，电导率为0.02 S/m，其他不变，相对介电常数实部引起的温度变化如图12所示。可以看出，随着相对介电常数实部增大，升温速率减小。这是由于介电常数增大导致电场模减小 (如图 13所示)，从而电损耗减小。(2) 保持介电常数实部为2，电导率为0.02 S/m，其他不变，介电常数虚部引起的温度变化如图14所示。可以看出，随介电常数虚部增大，升温速率升高，升温速率主要受介电损耗的影响，如图15所示，2 s ～ 3 s之间介电损耗增大，升温速率升高，3 s ～ 6 s之间介电损耗减小，升温速率降低。

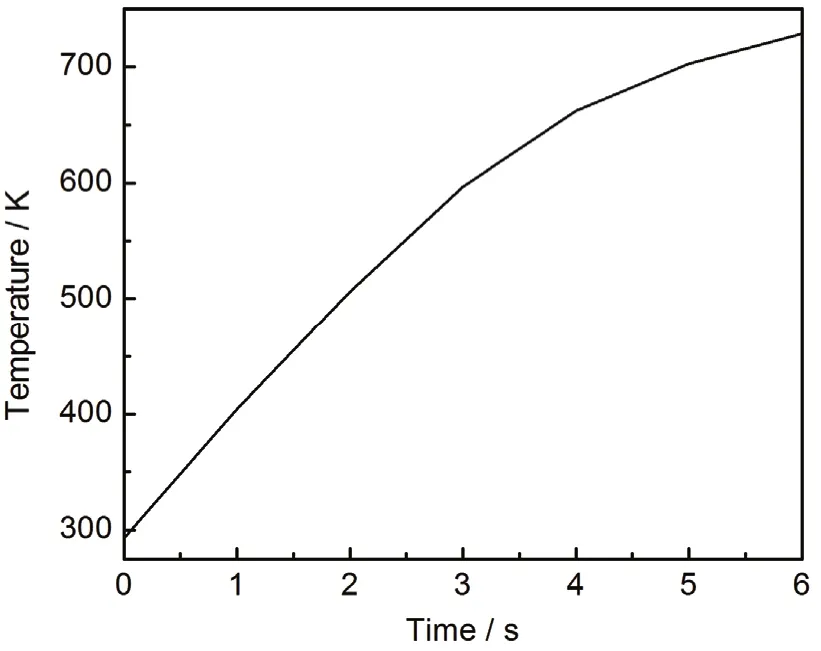
图12 中心点温度随时间的变化Figure12 Variation of center point temperature with time (ε″ = 0.1, σ = 0.02 S/m)

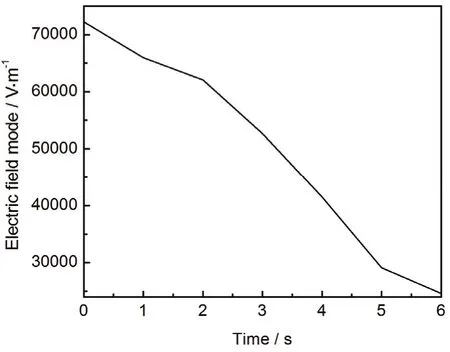
图13 中心点电场模随时间的变化Figure13 Variation of center point electric field mode with time (ε″ = 0.1, σ = 0.02 S/m)

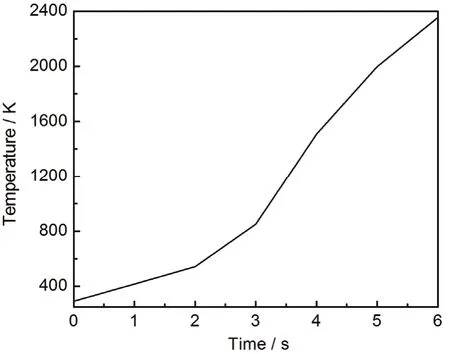
图14 中心点温度随时间的变化Figure14 Variation of center point temperature with time (ε′ = 2, σ = 0.02 S/m)

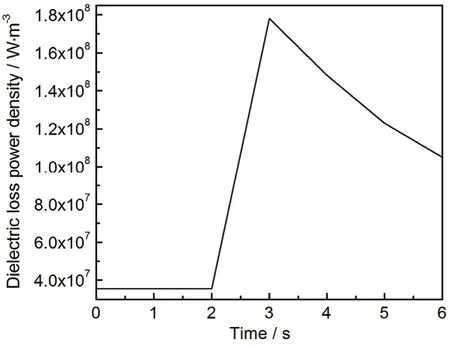
图15 中心点介电损耗功率密度随时间的变化Figure15 Variation of center point dielectric loss power density with time (ε′ = 2, σ = 0.02 S/m)

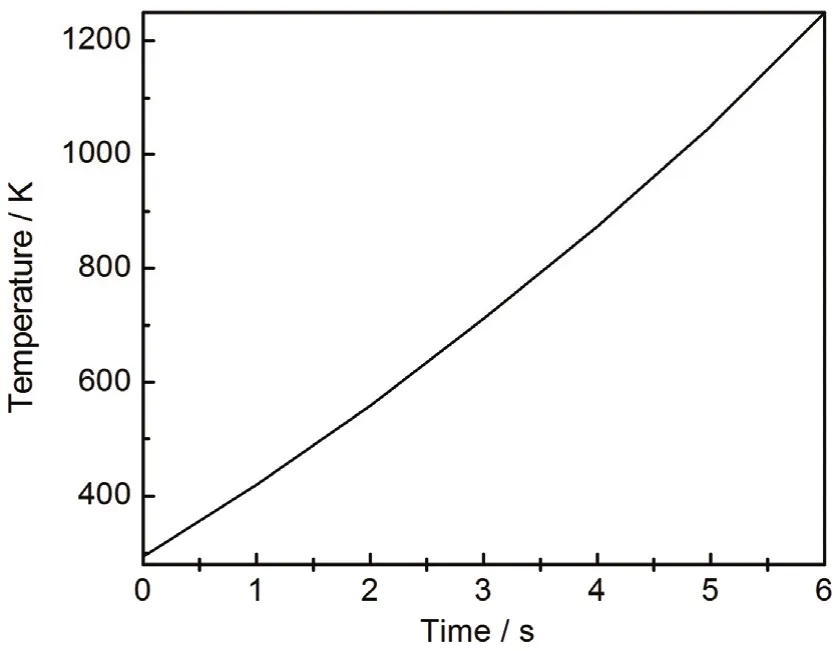
图16 中心点温度随时间的变化Figure16 Variation of center point temperature with time (εc = 2 - 0.1j)

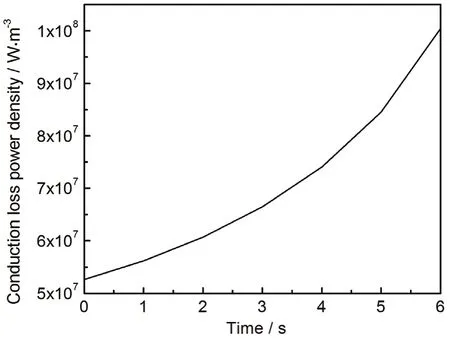
图17 中心点电导损耗功率密度随时间的变化Figure17 Variation of center point conduction loss power density with time (εc = 2 - 0.1j)

3.2 电导率的影响

保持碳的复介电常数为εc= 2 - 0.1j，其他条件不变，得到的中心点升温速率如图16所示，电导损耗功率密度随时间的变化关系如图17所示。可以看出，电导率增大使电导损耗增大，相同时间内吸收更多的热量，从而升温速率升高。

3.3 微波输入功率的影响

改变微波输入功率分别为5000 W和7500 W，中心点温度随时间的变化关系分别如图18和图19所示。比较图18、图19和图7可以看出，随着微波输入功率的增大，升温速率分别在5 s、4 s、3 s时开始增大，相应的其电损耗也在对应时间点开始增大，6 s时达到最大温度，分别为660 K、1000 K、1250 K，说明增大微波输入功率可以提高升温速率，并且能更快达到最大升温速率。

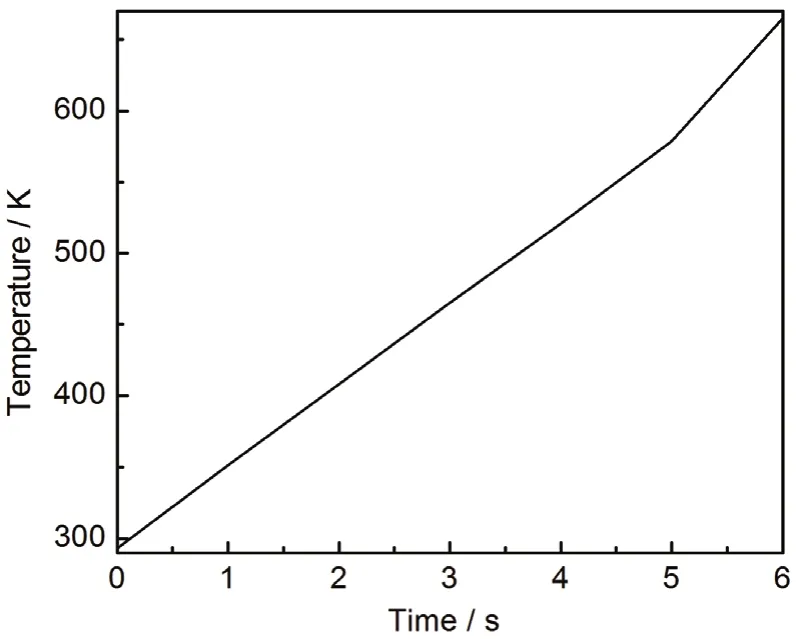
图18 中心点温度随时间的变化Figure18 Variation of center point temperature with time (microwave power 5000 W)

图19 中心点温度随时间的变化Figure19 Variation of center point temperature with time (microwave power 7500 W)

3.4 保温结构的影响

不加保温层的碳与空气之间存在热交换。在这种情况下，中心点温度随时间的变化关系如图20所示。比较图7和图20可知，由于热交换的影响，无保温结构的碳升温速率有所降低，但温度总体变化趋势不变。

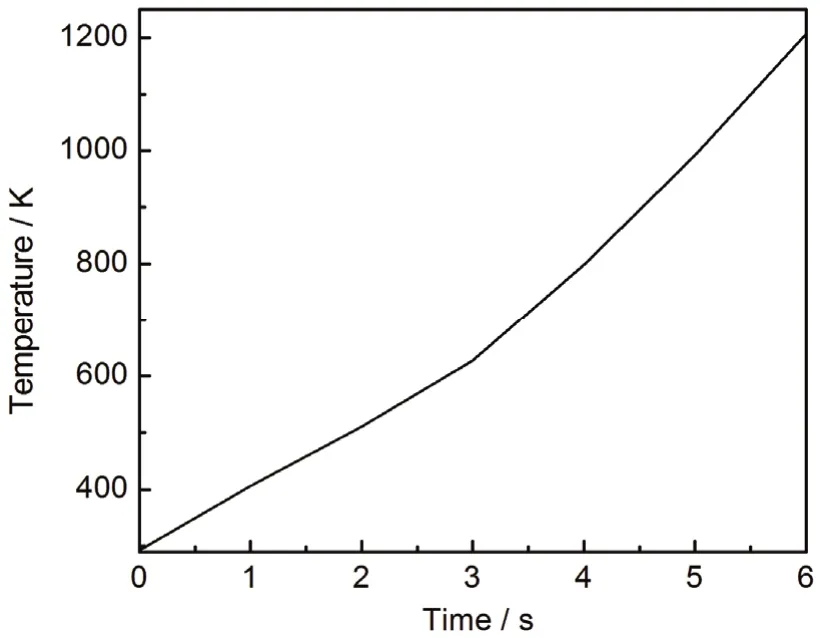
图20 中心点温度随时间的变化Figure20 Variation of center point temperature with time (without insulating layer)

3.5 杂质的影响

材料在制备过程中难免存在杂质。选取Al2O3为杂质成分，其相对介电常数实部和损耗角正切值随温度变化关系分别如图 21和图 22所示[21]，内插和外延部分均为阶段线性变化。

在圆柱形碳内部均匀选取6个点作为Al2O3掺杂点，模型如图23所示。分析发现，微波加热6 s后，系统的最高温度可以达到1460 K (图24)。掺杂之后温度梯度大幅降低 (图25)，中心点最大温度梯度则由掺杂前的28000 K/m下降到掺杂后的4000 K/m，温度沿弧长的变化平缓(图 26)。

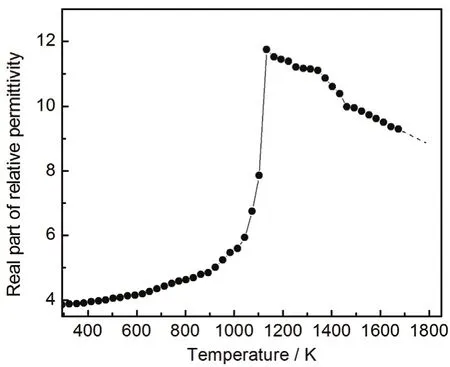
图21 Al2O3相对介电常数实部随温度的变化Figure21 Variation of real part of relative permittivity with temperature for Al2O3

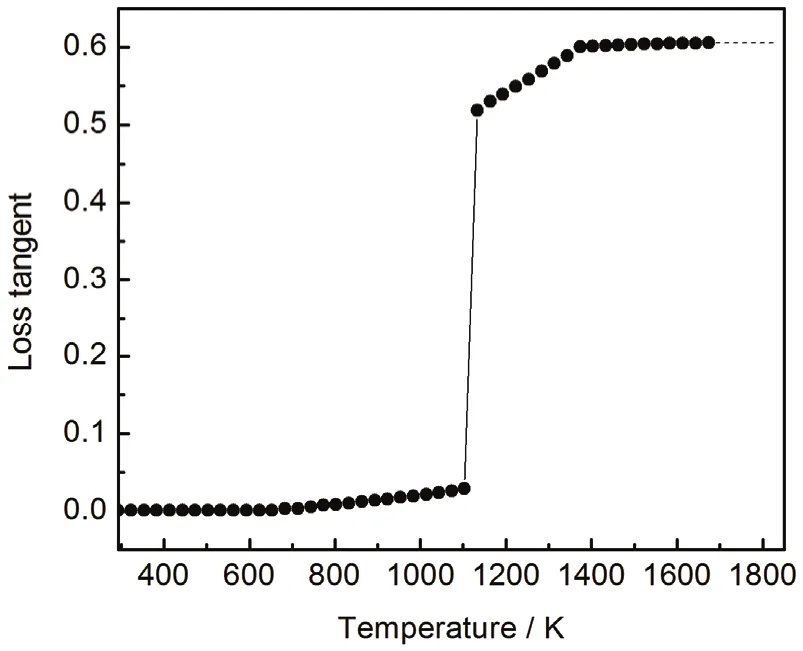
图22 Al2O3损耗角正切随温度的变化Figure21 Variation of loss tangent with temperature for Al2O3

图23 Al2O3掺杂点Figure23 Positions for Al2O3 doping (6 points)

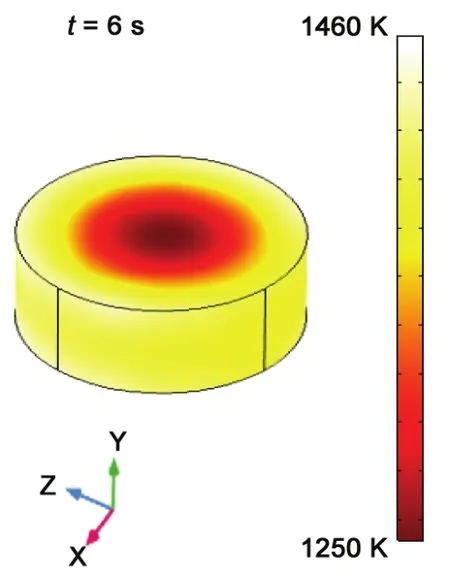
图24 掺杂Al2O3的碳在微波加热6 s时的温度分布Figure24 Temperature distribution in A2O3-dopied carbon being microwave heated for 6 s (6 points)

图25 中心点温度梯度随时间的变化Figure25 Variation of center point temperature gradient with time (Al2O3 doping, 6 points)

图26 温度随弧长的变化Figure 26 Variation of temperature with arc length(Al2O3 doping, 6 points)

如果如图27所示选取12个Al2O3掺杂点，则中心点温度梯度较6个掺杂点时进一步减小，最大温度梯度仅为3600 K/m，各部分温度变化更加平缓，如图28所示。

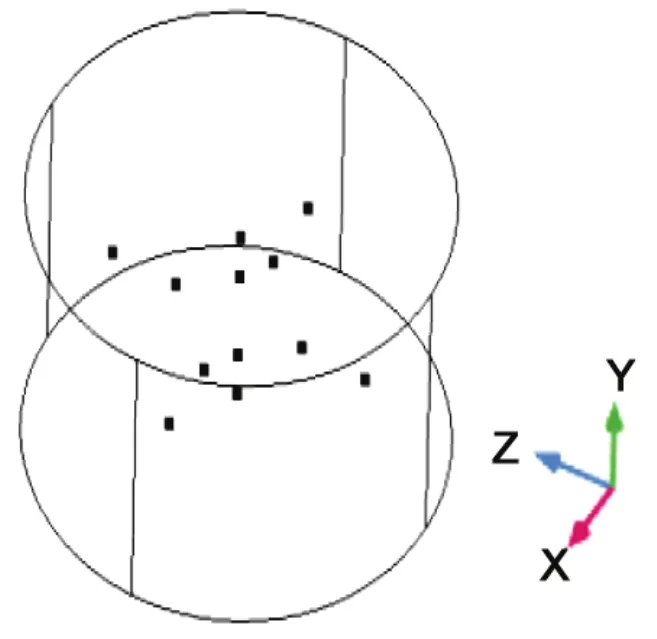
图27 Al2O3掺杂点Figure27 Positions for Al2O3 doping (12 points)

图28 温度随弧长的变化Figure28 Variation of temperature with arc length(Al2O3 doping, 12 points)

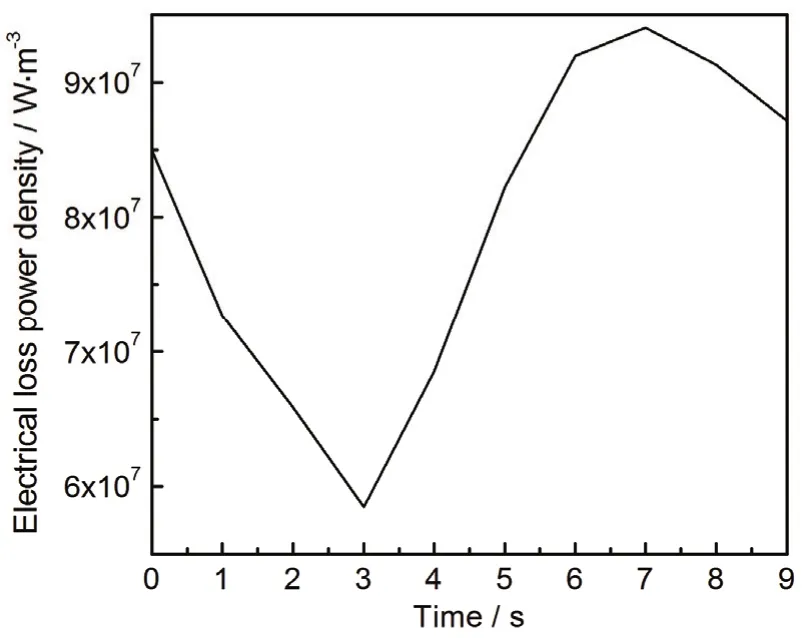
图29 中心点电损耗功率密度随时间的变化Figure29 Variation of center point electric loss power density with time (up to 9 s)

图30 中心点温度随时间的变化Figure30 Variation of center point temperature with time (up to 9 s)

3.6 加热时间的影响

延长微波加热时间至9 s，模拟分析结果如图29和图30所示。可以看出，中心点电损耗功率密度在7 s时开始减小，升温速率在7 s时也开始降低。

4 结 论

根据Maxwell方程组计算出各种损耗功率密度和电磁能量，运用COMSOL软件模拟出不同条件下碳的微波损耗特征和温度变化规律，模拟结果与理论计算值符合较好，可以得出以下结论：

(1) 微波加热是整体加热，温度由内而外依次升高，温度梯度先增加后减小，最终温度趋于一致。

(2) 微波损耗功率密度与升温速率成正相关，碳的微波损耗主要是介电损耗。

(3) 随复介电常数和电导率的增大，碳的电场模减小，电导损耗与电场模的减小趋势基本一致，所以电导损耗功率密度与电场模在碳内部的大小分布基本相同。

(4) 介电常数实部单独增大时，电场模减小，介电损耗和电导损耗减小，升温速率降低；介电常数虚部单独增大时，电场模减小，介电损耗先增大后减小，升温速率先升高后降低。

(5) 电导率单独增大时，电场模减小，电导损耗增大，升温速率提高。

(6) 微波输入功率减小时，各种损耗功率密度减小，损耗功率密度开始增大时间点延长。

(7) 增加保温结构和Al2O3掺杂点以及适当延长加热时间都能提高碳的升温速率，减小温度梯度。

[1] FAN J, WU X, CHU P. Low-dimensional SiC nanostructures: fabrication, luminescence, and electrical properties [J]. Progress in Materials Science, 2006, 51: 983-1031.

[2] SU X, ZHOU W, LUO F, et al. A cost-effective approach to improve dielectric property of SiC powder [J].Journal of Alloys and Compounds, 2009, 476: 644-647.

[3] ZHAO D, LUO F, ZHOU W. Microwave absorbing property and complex permittivity of nano SiC particles doped with nitrogen [J]. Journal of Alloys and Compounds, 2010, 490: 190-194.

[4] TAN E, KAGAWA Y, DERICIOGLU AF. Electromagnetic wave absorption potential of SiC-based ceramic woven fabrics in the GHz range [J]. Journal of Materials Science, 2009, 44: 1172-1179.

[5] ZHU HL, BAI YJ, LIU R, et al. In situ synthesis of one-dimensional MWCNT/SiC porous nanocomposites with excellent microwave absorption properties [J]. Journal of Materials Chemistry, 2011, 21:13581-13587.

[6] ACHESON G. Production of artificial crystalline carbonaceous material; 美国US492767 [P]. 1893.

[7] ALLIEGO RA, COFFIN LB, TINKLEPAUGH JR. Pressure-sintered silicon carbide [J]. Journal of the American Ceramic Society, 1956, 39: 386-389.

[8] CHAMMOND S, CARRY CP, BOUVARD D. Densification and microstructure evolution of Y-tetragonal zirconia polycrystal powder during direct and hybrid microwave sintering in a single-mode cavity [J].Journal of the European Ceramic Society, 2010, 30: 1211-1221.

[9] ZUO F, CARRY C, SAUNIER S, et al. Comparison of the microwave and conventional sintering of alumina: effect of Mg O doping and particle size [J]. Journal of the American Ceramic Society, 2013, 96:1732-1737.

[10] CHEN Y, FAN B, SHAO G, et al. Preparation of large size ZTA ceramics with eccentric circle shape by microwave sintering [J]. Journal of Advanced Ceramics, 2016, 4: 1-7.

[11] TOURADJ E, EHSAN MR. Microwave hybrid synthesis of silicon carbide nanopowders [J]. Materials Characterization, 2009, 60: 69-72.

[12] SATAPATHY LN, RAMESHA PD, DINESH A, et al. Microwave synthesis of phase-pure, fine silicon carbide powder [J]. Materials Research Bulletin, 2005, 40: 1871-1882.

[13] DAI CH, ZHANG XP. Microwave synthesis of ultrafine silicon carbide whiskers [J]. Journal of the American Ceramic Society, 1997, 80: 1274-1276.

[14] MOSHTAGHIOUN BM, POYATO R, CUMBRERA FL, et al. Rapid carbothermic synthesis of silicon carbide nano powders by using microwave heating [J]. Journal of the European Ceramic Society, 2012, 32:1787-1794.

[15] ACILGOZ H, BIHAN YL, MEYER O et al. Microwave finite element modeling: applications to coupled electromagnetic-thermal problems and characterization of dielectric materials [R]. Presented at 12th Seminar Computer Modeling in Microwave Engineering & Applications. France, Grenoble, 2010.

[16] BOUVARD D, CHAMMOND S, CARRY CP. Multiphysics simulation of microwave sintering in a monomode cavity[R]. Presented at 12th Seminar Computer Modeling in Microwave Engineering &Applications. France, Grenoble, 2010.

[17] LOVAS M, KOVACOVA M, DIMITRAKIS G, et al. Modeling of microwave heating of andesite and minerals [J]. International Journal of Heat & Mass Transfer, 2010, 53 (17–18): 3387-3393.

[18] 罗凌霄. 介质损耗与电磁能量[J]. 大学物理, 2010, 29 (1): 13-15.

[19] 王晴东, 王光华, 陈彪, 等. 东胜褐煤与Yallourn褐煤热解过程中微波吸收特性[J]. 煤炭学报, 2016,41 (6): 1540-1545.

[20] 徐龙君, 刘成伦, 鲜学福. 频率对突出区煤导电性的影响[J]. 矿业安全与环保, 2000, 27 (6): 25-26.

[21] 吕晶. 微波烧结 Al2O3陶瓷过程中介电性能温变规律的模拟研究[D]. 青岛: 青岛大学硕士学位论文,2016.