基于Udwadia-Kalaba理论的隔振平台动力学研究

黄 康，刘伟炜，王卫荣，朱凌坤，葛新方

(合肥工业大学 机械工程学院，合肥 230009)

近年来，随着微制造技术和精密测量技术的飞速发展，精密隔振系统已成为一个十分重要的研究课题。国内外许多学者已经对微制造隔振平台展开研究[1]。对于微制造隔振平台，在其生产制造过程中，实验室或工厂内的人员走动不可避免会产生微小振动，这个微小振动传递到微振动平台会对微制造的加工精度有一定影响，因此人行激励对微制造平台的影响不能忽视[2]。在此基础上运用Udwadia-Kalaba方法[3-4]进行微制造隔振平台离散化动力学建模，将微制造隔振平台模型简化为简单运动模型，并且不需要考虑整个系统自由度之间的耦合，过程简单，不易出错；另一方面，在将系统约束转化为约束力的过程中不必考虑拉格朗日乘子，容易确定约束力。该方法在约束系统动力学建模上可广泛应用。最终求解得到固连结构各质点的位移响应曲线，与分散结构的各质点位移响应曲线对比，可以得到良好的减振效果。

1 微制造隔振平台结构

以长春光机所的光栅刻划机为例介绍微制造隔振平台的结构，光栅刻划机位于隔振平台上，其整体装置放置在一个较为密闭的实验室内的一个深坑中，为了保证光栅刻划机的加工精度，在深坑的四周布置镂空的地板，用于隔绝实验室内的气流，隔振平台下面垫有砂石等一些减振材料，具体结构见图1。

图1 光栅刻划机结构装置简图

在微振动隔振平台离散化的模型中，对于每个质点所建立的双层隔振系统的第2层质量块之间是相互独立的，这种结构称为分散结构，如图2所示。

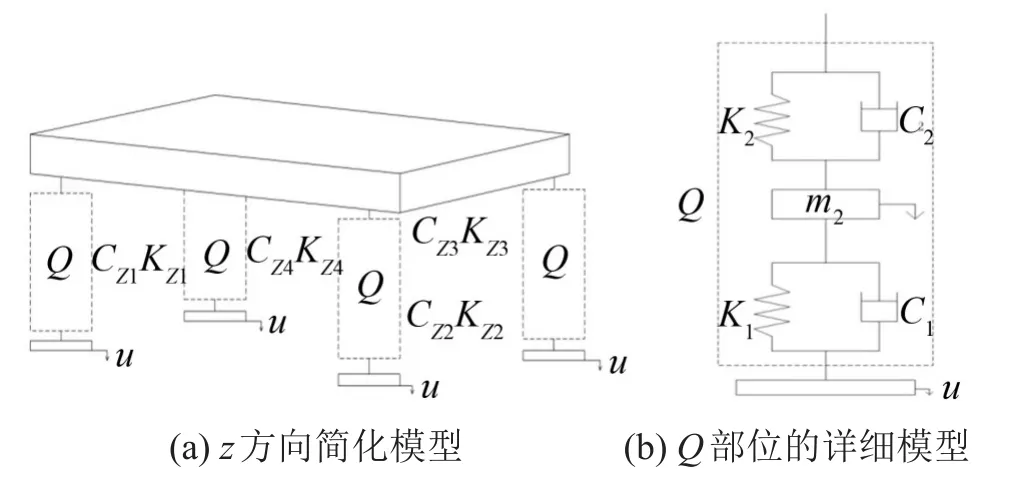
图2 微制造隔振平台分散结构模型图

而另一种为固连结构，双层隔振机构中4个质点的第2层简化的质量块不是相互独立的，为了进一步减小振动的影响，使其相互固连在一起，即第2层的4质点位于一个平面上，如图3所示。

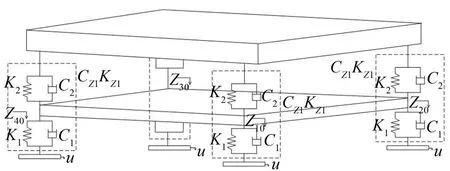
图3 微制造隔振平台固连结构模型图

这样在设计之初就可认定固连结构对环境振动的减振效果更加明显，而对于分散式结构，第2层等效质量块各自独立，对每个质点的振动会造成一定的副作用，导致在环境振动控制方面相互影响，造成振动加剧，进而对微制造设备的精度起破坏性的作用。

本文中平台的质量为m，各边的边长为2l。每个空气弹簧各个方向所具有的刚度和阻尼是相同的，分别为kx、ky、kz和cx、cy、cz。

2 U-K动力学方程

无外力约束系统运动方程为

有外力约束系统运动方程为

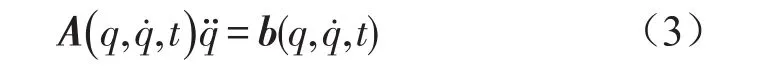
式中：q为n维向量，表示系统的自由度；t为时间变量；M(q,t) 为n×n维正定矩阵；为广义主动力矩阵；为m×n维矩阵，m为约束力的个数；为m维矩阵

由式（1）、式（2）、式（3）式可得系统运动方程为

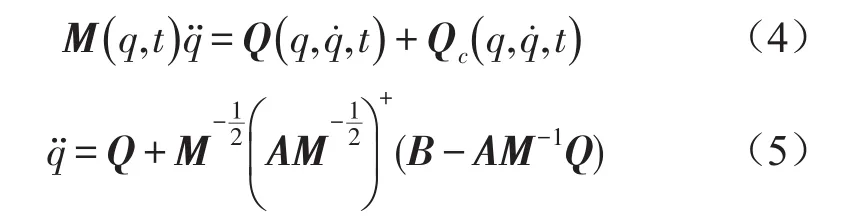
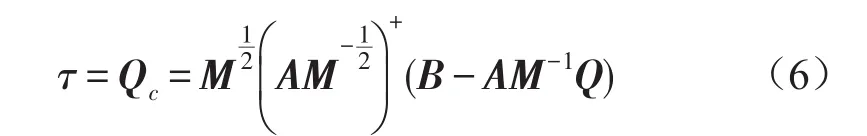
3 隔振平台结构的简化

对于人员的走动问题主要考虑的是竖向荷载，竖向人行荷载是由单个人体重加上一个波动周期分量，而整个人群荷载是由单个人行荷载乘以一个放大系数，综上群荷载总的有效竖向力计算公式如下

上式中：N为任意时刻实验室或工厂内的人员数，fv为地板所具有的竖向固有频率。

结合图2所示，微制造隔振平台整体结构简化成在行人激励下的单质点的等效模型，将双层隔振模型与底座看作一个整体，简化的单自由度模型见图4。

图4 单质点的等效模型

其中固连结构中m2连接在一起；分散结构m2分散布置。

M的位移响应曲线很容易得到；具体等效参数为N为4；M为1 000 kg；K为200N/mm；C为100N·s/mm ；fv选为2.0 Hz；然后计算所得

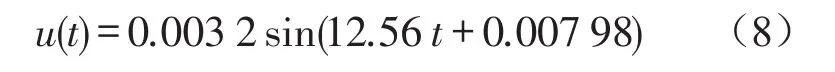
针对Z方向的振动，4个质点共有8个自由度，由4个质点的U-K动力学方程可得

4 仿真

设置具体的仿真参数，并将参数代入到MATLAB软件中进行仿真。

表1 仿真数据

具体的约束为：z1、z2、z3、z44个自由度位于一个平面上，而且其z10、z20、z30、z404个自由度也同样位于一个平面上，最终确定其离散化模型的z方向8个自由度的具体的约束形式是

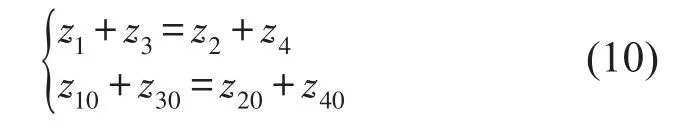
上式对时间求2阶导数，可以得到2阶约束形式为

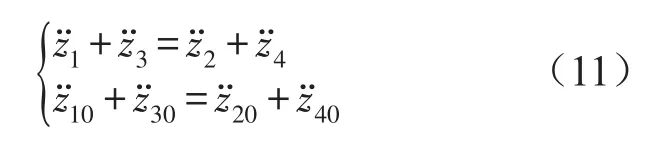
将以上两式代入有外力约束系统运动方程式（3）中

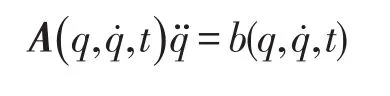
其中微振动隔振平台各自由度的初始条件具体如下

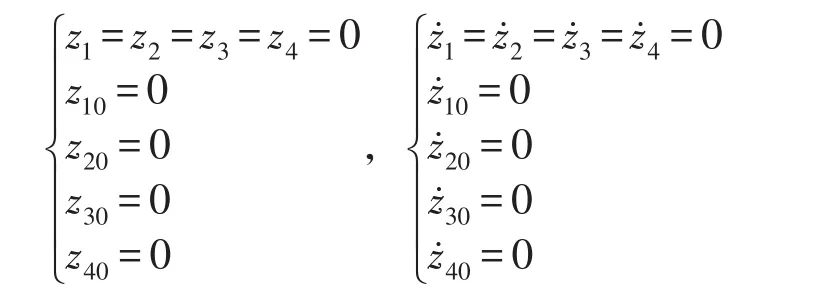
根据U-K动力学方程，可得到8个自由度的位移响应曲线，其分别是z1、z2、z3、z4、z10、z20、z30、z40。下图为固连结构和分散结构的位移响应曲线的对比图，从对比图上可以看出固连结构能起到良好的减振作用。

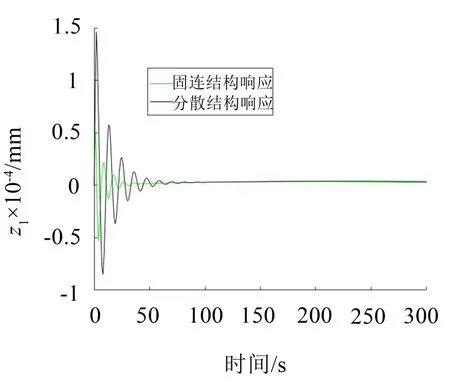
图5 z1的位移响应曲线

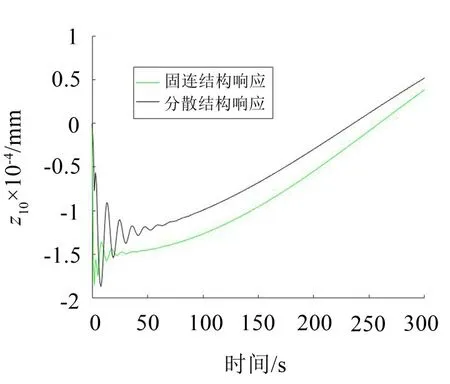
图6 z10的位移响应曲线

5 结语

（1）从图5、图7、图9、图11对比中可以看出固连结构与分散结构相比，固连结构能达到良好的减振效果；但是从图6、图8、图10中可以看出，其位移响应曲线相比原来的自由振动响应曲线有所下降；而图12由于约束变化较大，所以其振动响应曲线变化比较大；

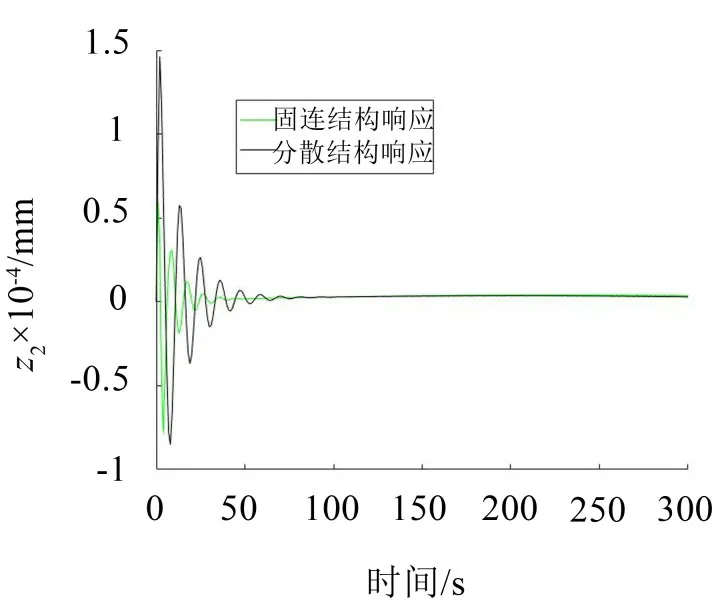
图7 z2的位移响应曲线

图8 z20的位移响应曲线

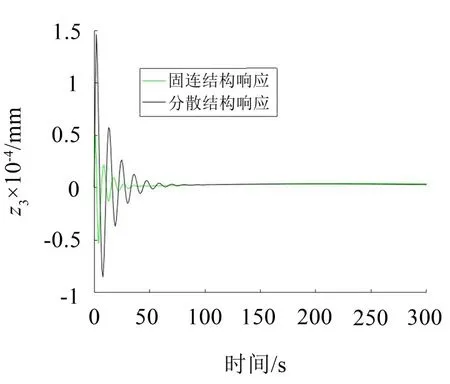
图9 z3的位移响应曲线

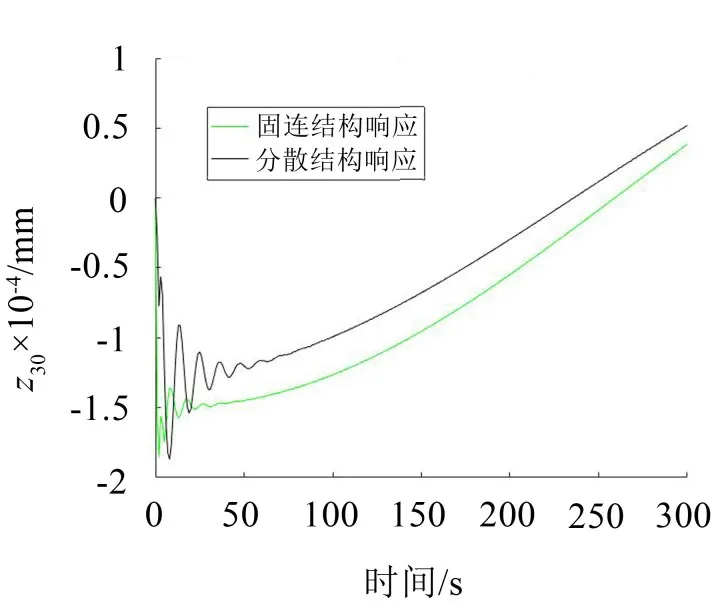
图10 z30的位移响应曲线

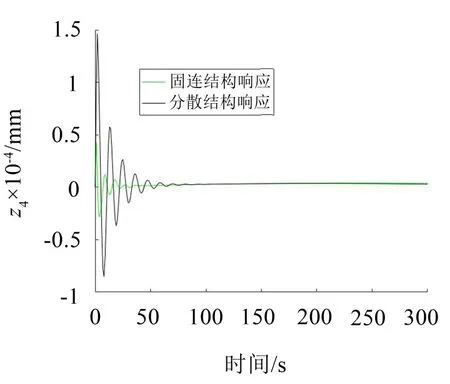
图11 z4的位移响应曲线

图12 z40的位移响应曲线

（2）由于微制造隔振平台最终的振动响应反映在z1、z2、z3、z44个自由度上面，从这4个自由度的对比图上，可以清楚地看出，人群激励所带来的振动被固连结构的第2层结构所吸收，从而起到了减振作用；而分散结构中的各个质点由于其第2层分散结构相互之间无约束，故起不到吸振作用；所以固连结构相比分散结构可以达到更好的减振效果。

参考文献：

[1]涂奉臣，陈照波，李华，等.新型整星隔振平台的被动隔振性能及星箭耦合特性分析[J].航空学报，2010，31(3)：538-545.

[2]孙利民，闫兴非.人行桥人行激励振动及设计方法[J].同济大学学报(自然科学版)，2004，32(8)：996-999.

[3]黄康，孙顺强，葛新方，等.采用Udwadia-Kalaba理论的微振动隔振平台研究[J].西安交通大学学报，2017，51(1)：1-58.

[4]UDWADIA F.On constrained motion[J].Applied Mathematics&Computation,2005,51(2):313-320.