基于部分加速度测量的结构Bouc-Wen非线性恢复力及质量识别

程骄阳，许 斌，贺 佳

(1.湖南大学 土木工程学院，长沙 410082； 2.华侨大学 土木工程学院，福建 厦门，361021；3.华侨大学 福建省结构工程与防灾重点实验室，福建 厦门，361021)

基于重大工程结构在强动力荷载下的动力响应监测数据进行损伤识别，是土木工程领域前沿课题之一。在强动力荷载作用后，根据结构的动力响应信息，运用一定的优化算法或分析手段识别结构参数的变化位置和程度，进而对结构中是否有损伤产生、损伤的定位和类型、损伤的严重程度进行判别，甚至评估结构的剩余寿命，是实现土木工程结构可持续发展的关键问题之一[1]。结构在强动力荷载作用下发生损伤时，往往会呈现复杂的非线性特征，通过识别非线性恢复力不仅可以获取损伤的发展过程还可对结构耗能进行定量评估。识别结构的非线性行为而不是传统基于振动测量的结构识别算法中的刚度，对结构灾后损伤识别具有重要意义。

结构的非线性行为相对更为复杂，而且由于结构材料和结构体系的多样性，结构非线性行为呈现出较大的差异性。较线性系统而言，结构非线性行为识别方法的研究时间相对较短，研究成果相对不成熟。针对非线性系统识别，最早的相关研究可以追溯到20世纪70年代[2]，之后，Masri和Caughey提出了著名的恢复力曲面法[3]，并推广应用到多自由度动力系统的非线性识别[4]。Yang和Ibrahim提出了相对更加简易的基于幂级数算法来识别振动系统的非线性行为[5]。Mohammad等在其基础上提出完全基于输入输出信息的直接参数识别法，有效识别了系统质量、刚度和阻尼等具体物理参数[6]。Xu和He等提出了利用结构动力响应时域信号，分别基于等价线性理论和幂级数多项式模型的结构非线性恢复力识别方法，通过数值模拟和实验数据对方法进行了验证，并考虑了测量不完备和部分激励未知时的识别方法[7-11]。许斌等研究基于切比雪夫多项式模型表征非线性恢复力的识别方法，获得了精度更高的识别结果并通过含MR阻尼器和SMA阻尼器的非线性多自由度系统验证了方法的有效性[12-14]。

大多非线性识别理论均基于完整的结构激励和响应信息。然而，在环境特殊、结构复杂情况下，由于传感设备布置的局限性，结构完整时域信息往往难以获得且含有不同程度噪声。基于状态空间模型的递推最小方差估计的卡尔曼滤波算法(Extended Kalman Filter，EKF)为解决这类问题提供了途径。Andrew提出基于EKF仅利用测量的加速度信息，进行滤波、估计即识别出结构参数[15]。Hoshiyam等在EKF的基础上提出了一种加权全局迭代的新方法，提高了识别精度[16]。尚久铨等针对复杂结构，采用缩减变量EKF进行降价处理，大大提升了计算效率[17]。Yang等学者提出了一种自适应追踪技术，结合最小二乘法识别未知激励与结构参数，且有效应用于非线性结构[18-19]。Lei等研究了基础隔震结构中橡胶隔震支座的非线性恢复力识别方法，通过数值模拟进行验证[20-22]。这类非线性结构识别方法进行参数识别时均是在结构质量已知的前提下进行的。然而在实际工程中，估算质量的误差会严重影响其他物理参数识别的准确性，研究仅利用部分响应信息对包括质量在内的结构非线性行为进行识别的方法更具一般意义。

针对传统EKF在识别结构非线性特性时需要已知结构质量，而基于最小二乘法的非线性恢复力识别方法须已知结构完整的响应信息的问题，本文提出一种结构质量、物理参数及非线性恢复力识别方法。首先利用质量估计值和部分观测加速度通过EKF预测结构完整的响应信息，再基于最小二乘法识别结构质量、物理参数（刚度、阻尼、非线性参数）进而得到非线性恢复力。通过对初始质量进行修正，循环迭代至收敛，最终实现了对结构质量和非线性恢复力的识别。通过在一个多自由度系统中引入Bouc-Wen磁流变阻尼器形成非线性结构数值模型，在质量初始误差不同并混入测量噪声的情况下进行数值模拟，证明该方法的有效性和抗噪性。

1 扩展卡尔曼滤波算法(EKF)

EKF算法具有预测和校正的功能，它适用于非线性系统的状态估计和模型辨识。利用部分观测信息，通过滤波估计，识别非线性系统的时程响应和物理参数。

一个多自由度非线性结构的运动方程可表示为

式(2)、式(3)中：Xk、Yk分别为状态向量和观测向量，Wk、Vk分别为过程噪声和测量噪声，通常假定为零均值高斯白噪声，且协方差矩阵分别为Qk、Rk。

g[X(t)，f(t)，t]可由状态向量X(t)对时间求1阶导并结合式(1)推导出。

h(Xk,fk,tk)是基于tk时刻状态向量Xk和fk观测量的函数。

EKF算法在每个时间点包括时间更新和测量更新两个过程。递归算法通过在以下步骤的循环中实现。假设tk时刻的状态向量初始值相应的误差协方差矩阵为Pk|k。

1)时间更新过程

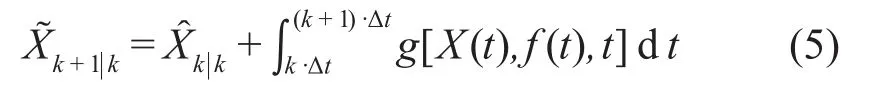
（2）预测误差协方差矩阵Pk+1|k

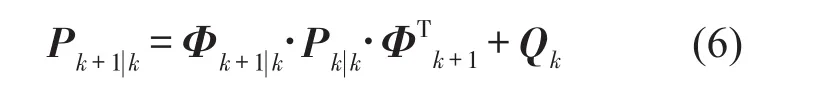
其中：Φk+1|k是状态转移矩阵，可由下式获得

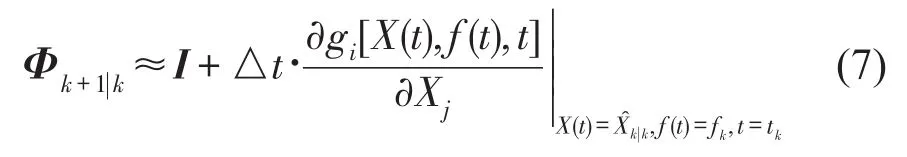
2)测量更新过程

（1）计算第k+1步的卡尔曼增益矩阵Kk+1

观测方程的系数矩阵Hk+1由下式求得

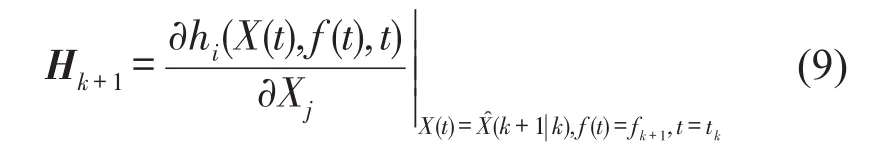
（2）用观测量更新tk+1=（k+1）t时刻的状态向量预估值，可以得到经过滤波估计后的状态向量

（3）更新误差协方差

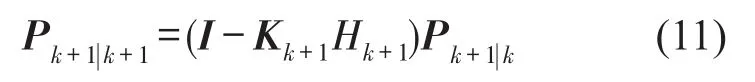
（4）令k=k+1，重复以上步骤直至k=s，s为观测数据点总数。

EKF算法通过以上两个过程的循环迭代，利用已知质量和有限的观测量，在获得结构完整的时程响应的同时通过递归求解得到结构参数。

2 基于最小二乘法的非线性恢复力识别方法

对s层作用有外激励的任意n自由度集中质量非线性动力系统，其运动方程可写为

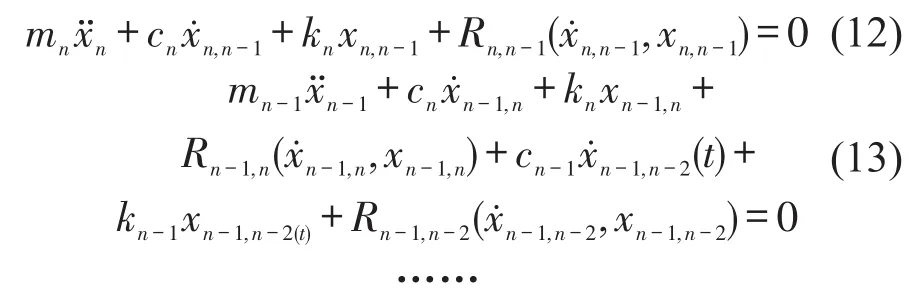
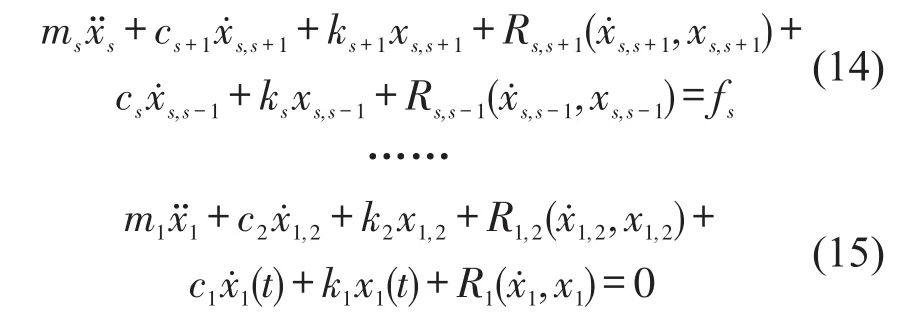
其中：mi、ki、ci分别为第i层的质量、刚度和阻尼，分别为结构第i层加速度、速度、位移响应，Ri为i层的非线性恢复力且是关于位移、速度、加速度的函数，fs为s层作用的外激励。分别为第n个和第n-1个自由度之间的相对位移和速度即

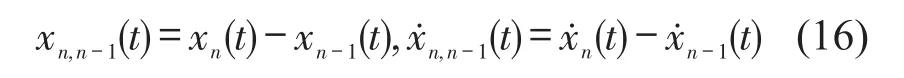
根据基于有限元列式的参数模型，每个自由度的运动方程均可表示为

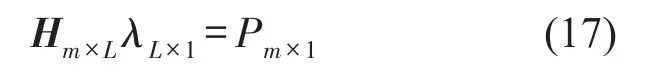
式中：H矩阵为响应矩阵，由式中的位移、速度、加速度响应构成；λ为待识别的系数向量；P为外激励向量；下标m为采样点数，L为待识别参数个数。

利用最小二乘法，结构参数可由下式识别

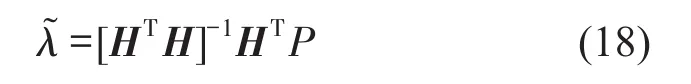
对于第s层，根据激励及相应的响应可识别出各未知参数。对于未受激励的自由度的运动方程，右边为0，无法直接运用最小二乘法，但可第k层的识别结果，且有

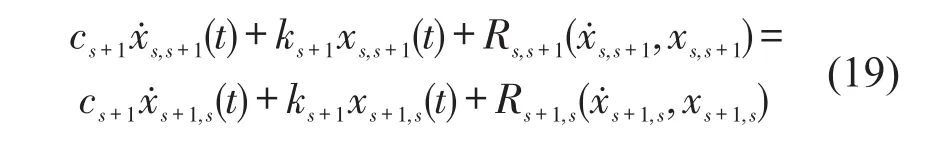
可代入s+1，s-1层方程，识别对应参数，依此类推，可以识别出结构剩余未知参数。

此方法可根据完整的时程响应信息识别出非线性系统各自由度的质量和总非线性恢复力。

3 基于EKF和最小二乘法的质量及非线性恢复力识别方法

传统EKF在识别结构非线性特性时往往依赖已知的结构质量，基于最小二乘法的非线性恢复力识别方法须知完整的响应信息。根据以上两种方法特点，本文提出一种结合两者的结构质量、物理参数及非线性恢复力的迭代识别方法。

在第j次迭代过程中，基于部分加速度观测值Am和质量估计值，完整的速度和位移时程可通过EKF算法获得，上标j表示第j次迭代。未观测的加速度信息可由EKF的识别结果计算得到。基于已获得系统完整的响应时程信息通过最小二乘法对质量分布进行识别，获得质量更新值借鉴增量补偿思想，引入学习因子γ∈(0,1)利用识别值对初始质量分布进行修正。

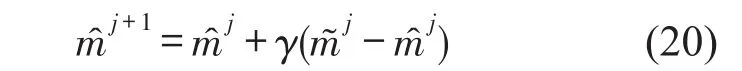
基于EKF和最小二乘法，通过迭代更新质量，在误差允许范围内，可获得最终的质量收敛值。利用质量收敛值mc，通过EKF算法识别出最终的时程响应信息和全部结构参数（刚度、阻尼、非线性参数）和非线性恢复力。

其具体步骤如下：

(2)利用步骤(1)的识别值，通过逆运算得到未知加速度时程

(3)由步骤(1)和(2)获得的完整时程信息，基于最小二乘法获得质量更新值

(5)基于质量收敛值mc，识别出最终时程响应信息、结构参数和非线性恢复力。

步骤流程如图1所示。

4 数值算例

4.1 计算模型与参数

如图2所示，以一个4自由度集中质量链式体系作为数值模型来验证方法的有效性和鲁棒性。在结构的第4层引入一个Bouc-Wen模型的磁流变阻尼器[23]来模拟结构非线性特性。Bouc-Wen阻尼器易于进行数值计算，通用性强，能反映各种滞回曲线。其滞回特性由以下运动方程表示

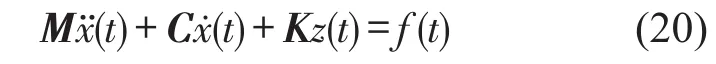
其中：K、C分别为结构整体的刚度矩阵和阻尼矩阵，滞回位移向量z具有遗传特性，其值变化取决于上一时刻的位移，且满足

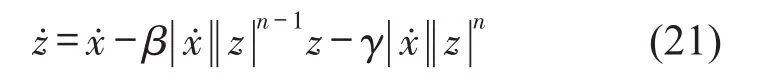
式中：n、β和γ为Bouc-Wen滞回参数，通过调整参数值可以控制滞回曲线的形状。

计算模拟中表征非线性系统性能的物理参数取值见表1，其中i=1,2,3,4。

采用随机激励，水平作用在第3个自由度上，时长为8 s，其时域图如图3所示。

图1 迭代算法流程图

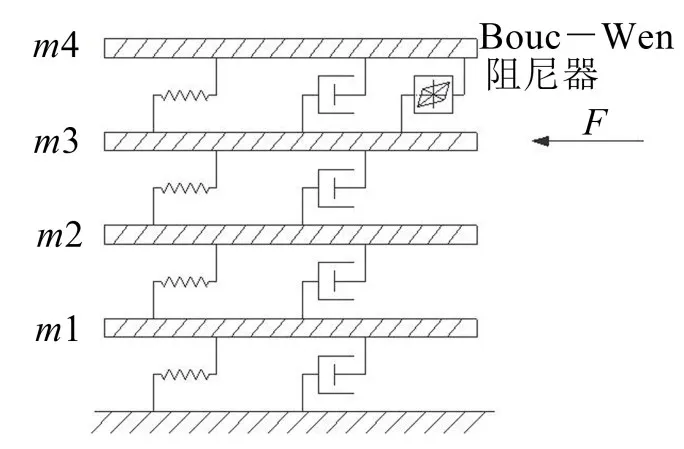
图2 计算模型

表1 数值模型参数

结构的时程响应采用4阶～5阶Runge-Kutta算法积分计算，积分步长为0.000 5秒。

识别过程中，EKF算法的结构状态向量定义为

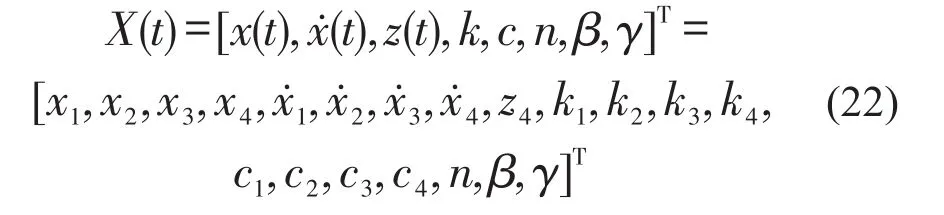
计算模型中由于只有第4层有非线性力，因此zi=xi(i=1,2,3)可在状态向量中省略。ki、ci、n、β和γ分别为待识别的阻尼、刚度和非线性参数向量。对t求1阶导数后，状态方程为

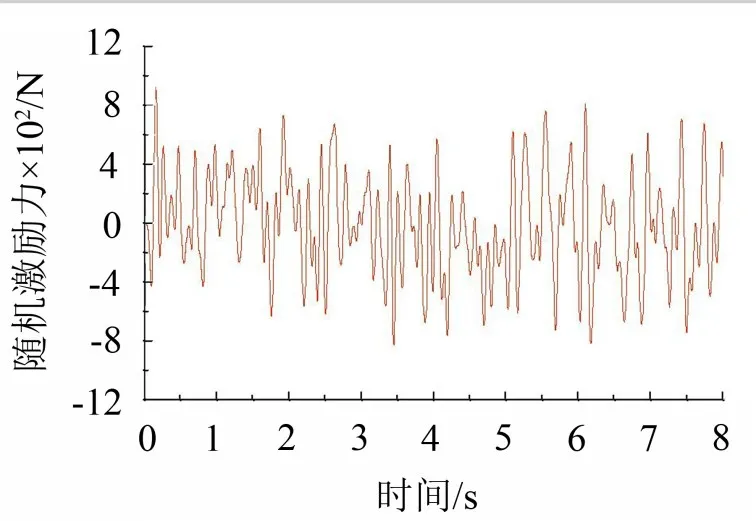
图3 结构随机激励荷载时程

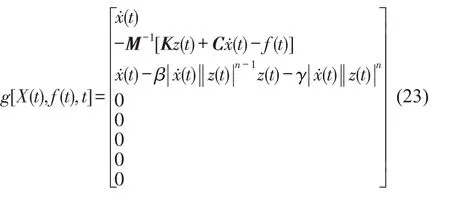
测量第2、第3、第4个集中质点上的加速度，为验证方法的鲁棒性，在观测向量中混入5%高斯白噪声。在观测方程中

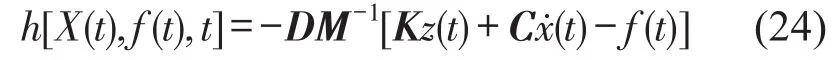
其中：D为加速度观测的位置矩阵。

本文中学习因子取为0.5，ε取为0.001。

4.2 工况1（质量初始误差为±10%)

由误差为±10%的质量初始值，通过文中方法获得质量的收敛值。图4表示质量收敛过程。

可以看出各自由度的集中质量均能随着迭代步数增加较好收敛于真实值，最终结果及误差如表2所示。

质量收敛后，由质量识别结果再次利用EKF算法，可识别出结构速度位移响应信息，并与算例真实值进行对比，结果如图5、图6。可见，速度和位移识别结果与真实值吻合很好。

在迭代过程中，利用最小二乘法识别方法时，需要知道完整的时程信息，其中未观测到的1层加速度信息是由前一步EKF方法获得识别结果反算得到。随着质量逐渐逼近真实值，1层加速度的估计值也愈加精确，图7表示在最后一步迭代时获得加速度与真实值的对比。最终获得的结构参数(刚度、阻尼、非线性参数)与真实值的对比以及计算得到的相对误差结果见表3。

表2 质量分布识别结果

可以发现，在部分观测加速度响应混入5%噪声的情况下各参数均有较好的识别精度，最大的识别误差也保持在2.5%之内。

根据识别得到的参数信息，可得到结构第四层Bouc-Wen阻尼器提供的非线性恢复力，并与真实值进行比较，结果如图8所示。

可以看出，阻尼器所提供的阻尼力的识别值与真实值非常接近。

4.3 工况2（质量初始误差为±15%)

工况2将初始质量的预估误差提高到±15%范围，同样在结构加速度响应中添加了5%的噪声，利用本方法获得的质量识别结果收敛曲线如图9所示。各层质量收敛值及误差见表4。

结构各层位移和速度响应以及未观测层的加速度响应时程以及与真实值的比较如图10至图12所示。

从对比可以看出，质量的识别结果具有很强的收敛性和稳定性，同时速度和位移响应时程识别结果也与真实情况高度吻合。结构各参数包括质量、刚度、阻尼、非线性参数的识别结果如表5所示。

阻尼识别的相对误差稍大，但是即使在5%的噪声等级下也只有2.55%的识别误差，参数识别仍具有很高的精度。Bouc-Wen阻尼器非线性恢复力识别结果与真实值的比较如图13所示。

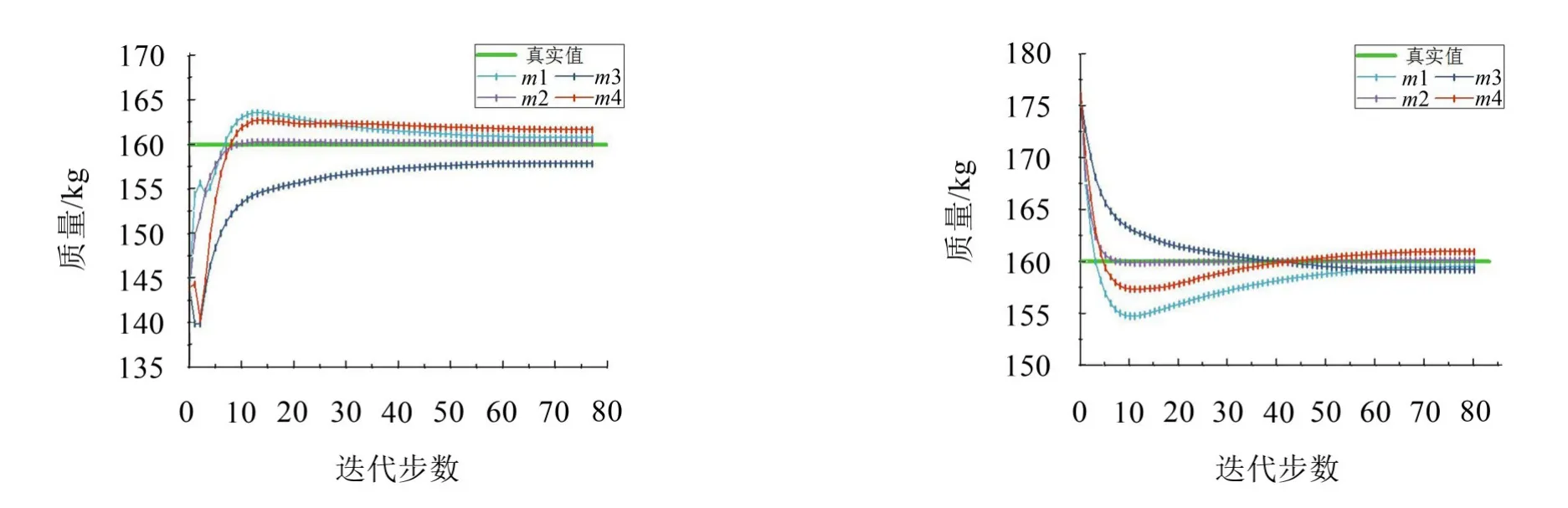
图4 质量收敛曲线图

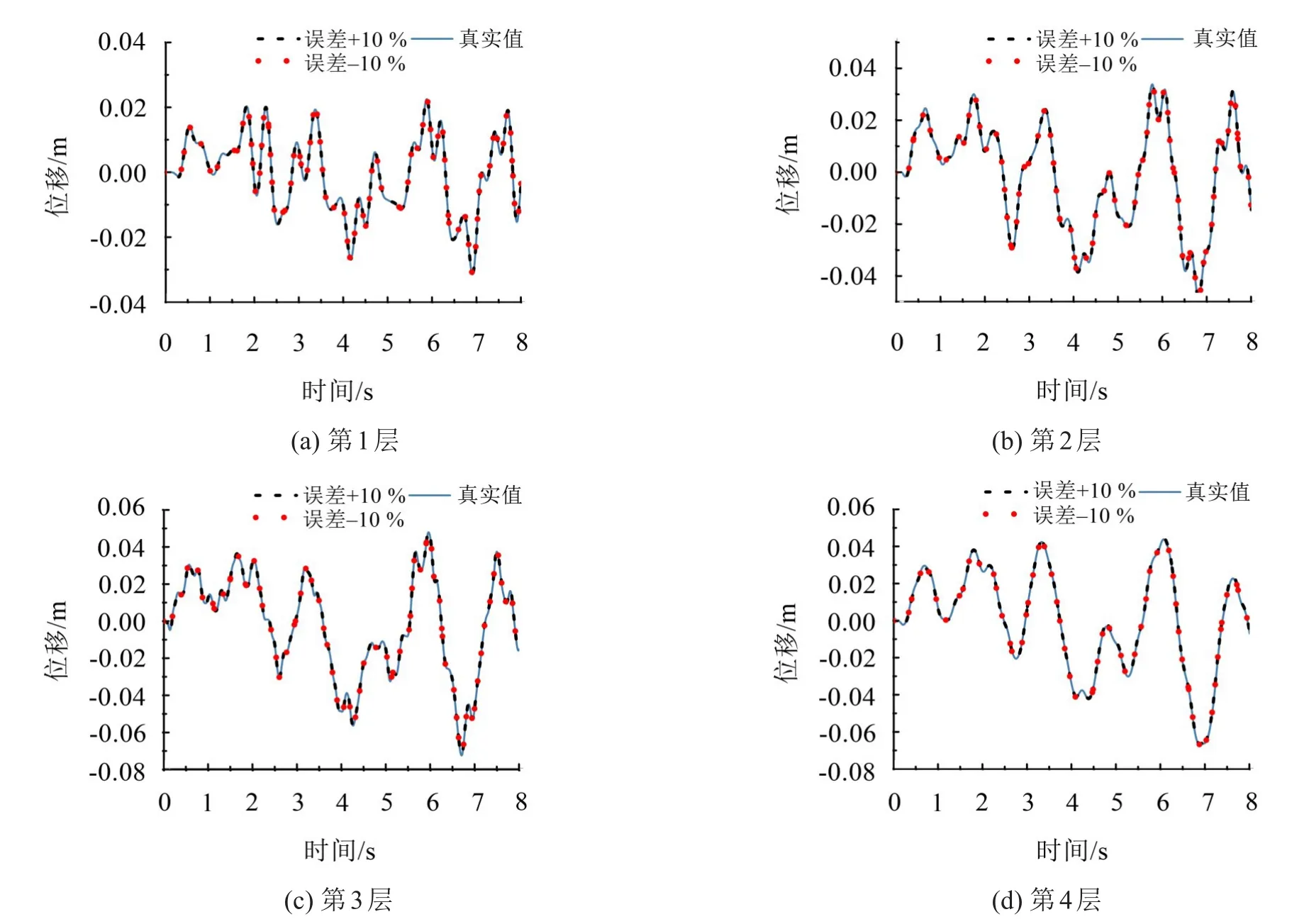
图5 结构位移响应识别结果

图6 结构速度响应识别结果

显然，即使在质量初始误差为±15%的情况下，本方法也可以很好识别结构质量、非测量加速度响应、速度和位移响应以及结构的非线性恢复力。

5 结语

结合EKF和最小二乘法算法，本文提出了一种仅利用外激励及结构部分响应加速度信息的结构质量、物理参数和非线性恢复力识别迭代方法。

表3 结构参数识别结果

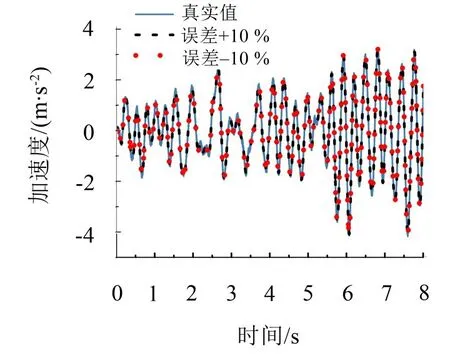
图7 第1层加速度响应识别值

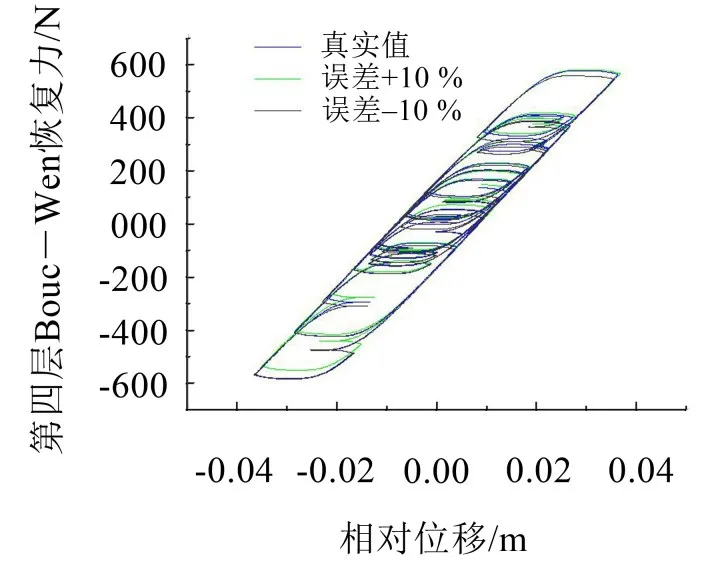
图8 MR阻尼器恢复力识别结果

图9 质量收敛曲线图

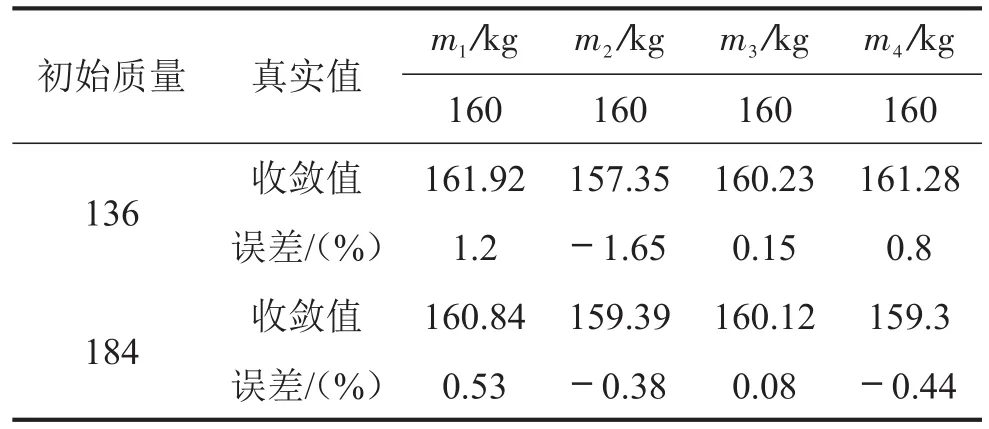
表4 质量分布识别结果

通过对一个含Bouc-Wen磁流变阻尼器的4自由度体系的非线性模型进行数值模拟，验证了方法的有效性。同时为证明该方法的鲁棒性，在观测的加速度响应信息中混入5%的高斯白噪声，并在质量初始误差在±10%、±15%情况下识别结构参数和非线性恢复力。结果表明，在随机激励作用下，该方法仅利用部分自由度上的加速度观测信息，最终实现对结构质量、物理参数（刚度、阻尼、非线性参数）和Bouc-Wen阻尼器提供的非线性恢复力的识别，识别精度高且具有良好的抗噪性。

本文所提出的方法可利用结构在动力荷载作用下的部分加速度响应测量，识别结构中非线性恢复力，可以用来直接反映动力荷载作用下结构损伤的发生、发展过程，而且非线性恢复力识别结果可对结构耗能和损伤程度进行定量评估，对工程结构在强动力荷载作用下的损伤状态和性能诊断具有重要意义。

表5 结构参数识别结果

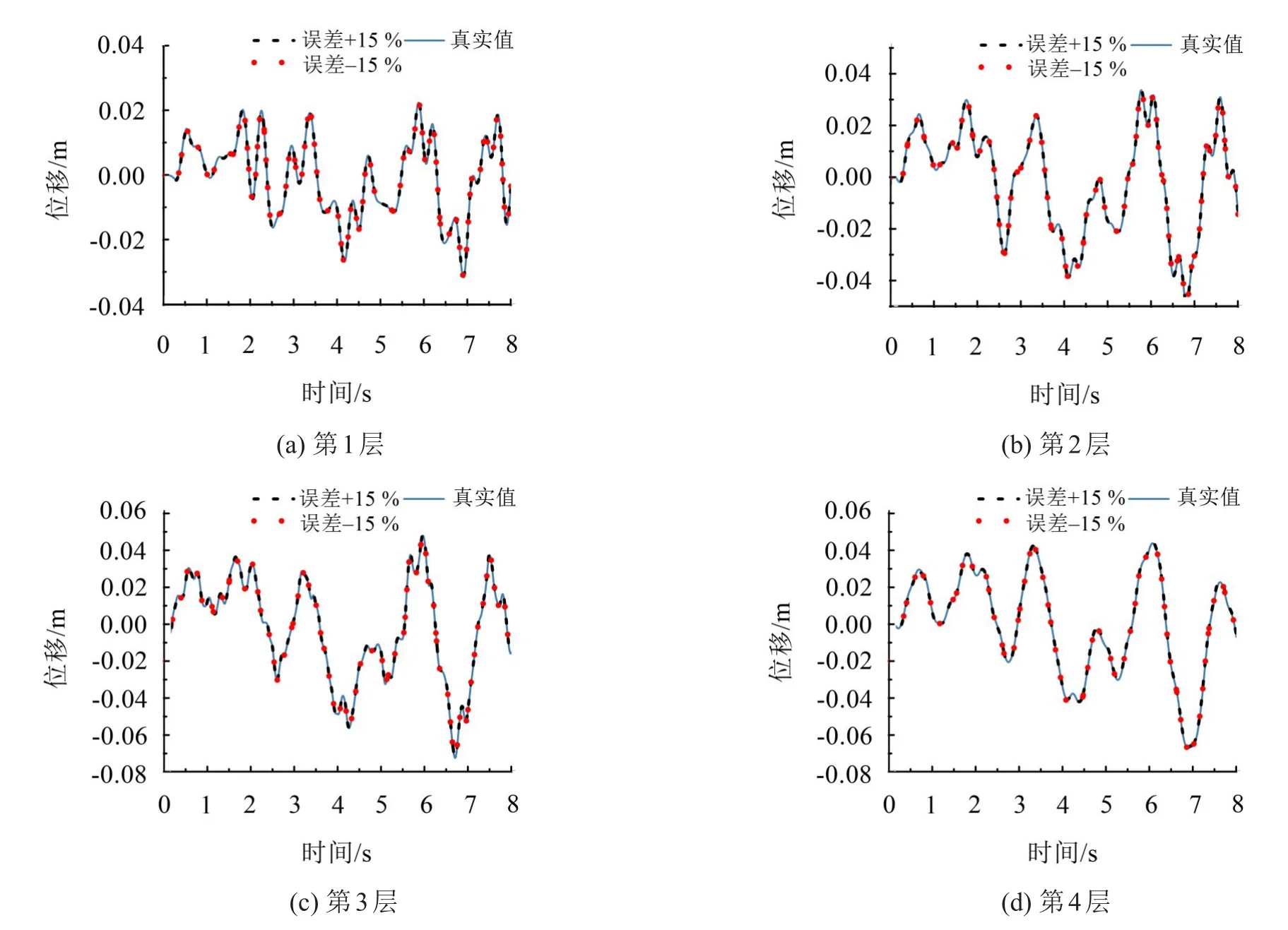
图10 结构位移响应识别结果

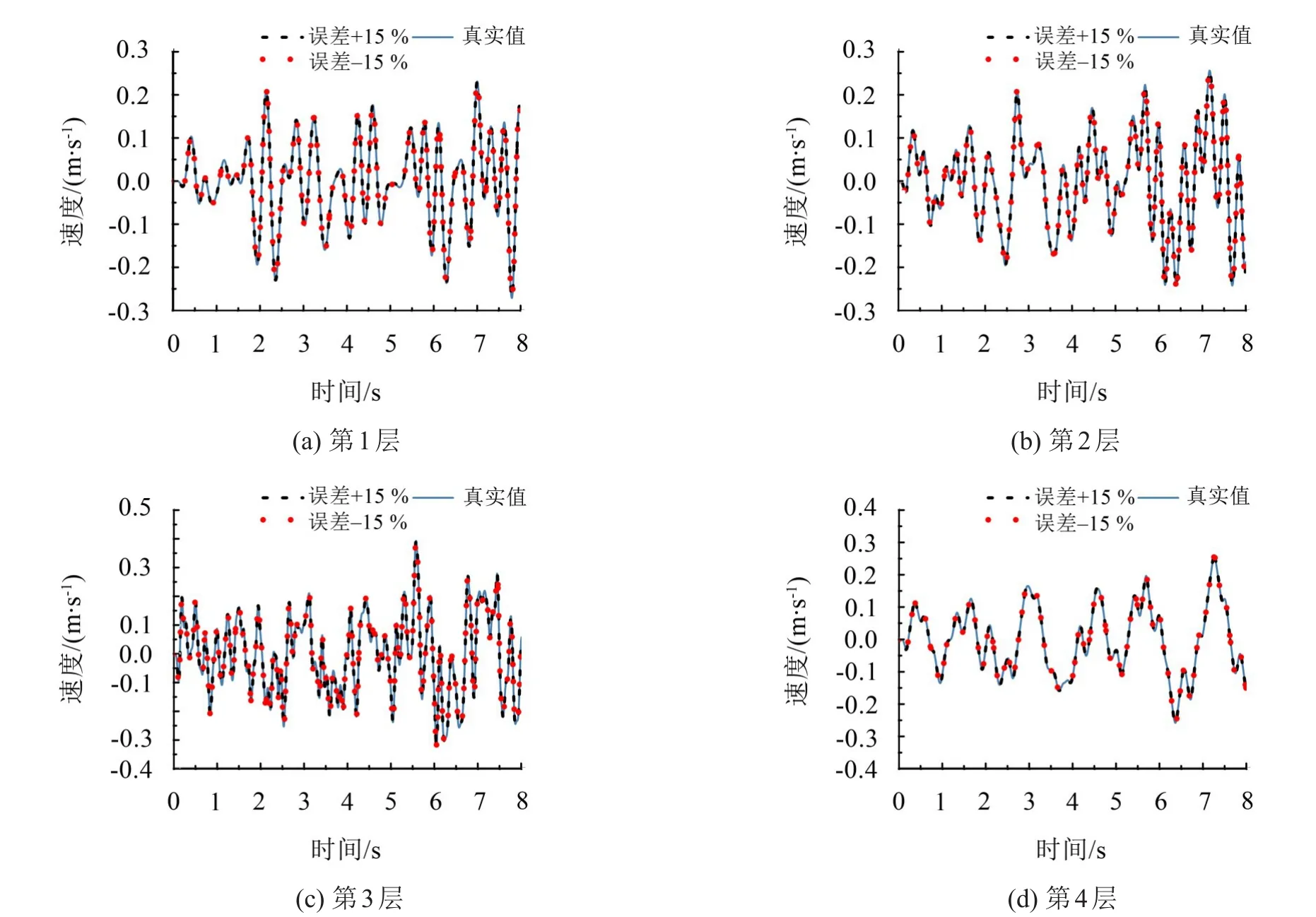
图11 结构速度响应识别结果

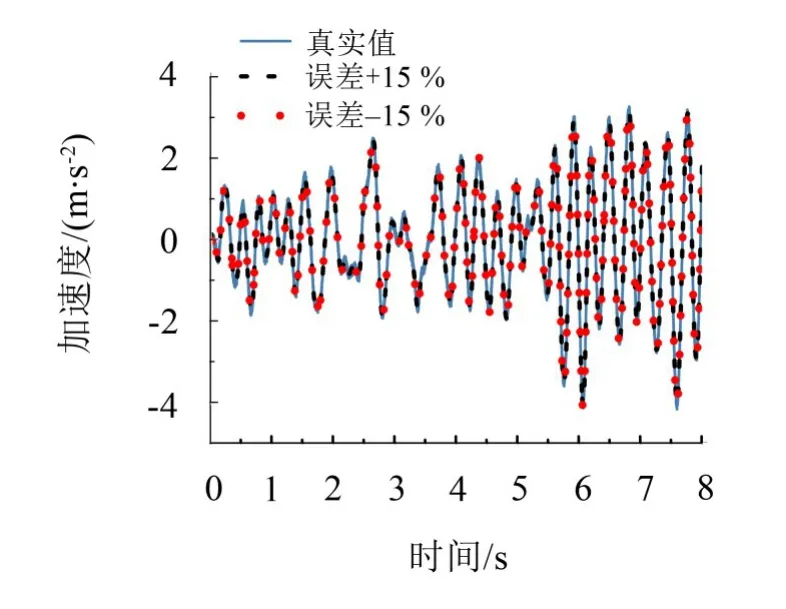
图12 第一层加速度响应识别值

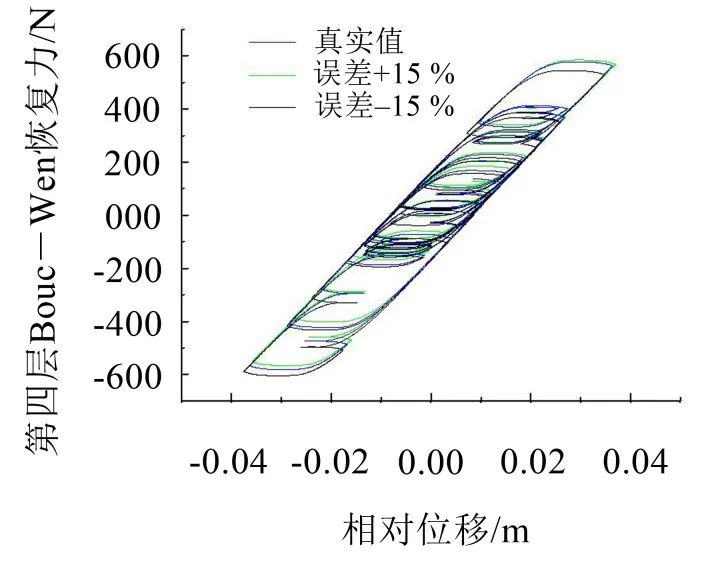
图13 MR阻尼器恢复力识别结果

参考文献：

[1]SOHN H,FARRAR C R.Damage diagnosis using time series analysis of vibration signals[J].Smart Material Structures,2001,10(3):446-451.

[2]IBÁÑEZ P.Identification of dynamic parameters of linear and non-linear structural models from experimental data[J].Nuclear Engineering&Design,1973,25(1):30-41.

[3]MASRISF,CAUGHEYTK.Anonparametric identification technique for nonlinear dynamic problem[J].Journal ofApplied Mechanics,1979,46(3):433-447.

[4]Masri S F,Sassi H,Caughey T K.Nonparametric identification of nearly arbitrary nonlinear systems[J].Journal ofApplied Mechanics,1982,49(5):619-628.

[5]YANG Y,IBRAHIM S R.A nonparametric identification technique for a variety of discrete nonlinear vibrating systems[J].Journal of Vibration,Acoustics,Stress,and Reliability in Design,1985,107(1):60-66.

[6]MOHAMMAD K S,WORDEN K,TOMLINSON G R.Direct parameter estimation for linear and non-linear structures[J].Journal of Sound&Vibration,1992,152(3):471-499.

[7]XU B,HE J,MASRI S F.Time domain data-based model free structural nonlinear performance identification[C].Proceeding of International Symposium on Innovation&Sustainability of Structures in Civil Engineering,2009:59-69.

[8]XU B,MASRI S F.Nonlinearity identification for a frame modelstructure with MR dampers underlimited excitations[C]. Asia-pacific young researchers &graduates symposium.2010,159-167.

[9]XU B,HE J,MASRI S F.Data-based Identification of nonlinearrestoring force underspatially incomplete excitations with powerseries polynomialmodel[J].Nonlinear Dynamics,2011,67(3):2063-2080.

[10]XU B,HE J,MASRI S F.Data-based model-free hysteretic restoring force and mass identification for dynamic systems[J].Computer-Aided Civiland Infrastructure Engineering,2015,30(1):2-18.

[11]HE J,XU B,MASRI S F.Restoring force and dynamic loadings identification for a nonlinear chain-like structure with partially unknown excitations[J].Nonlinear Dynamics,2012,69(69):231-245.

[12]XU B,HE J,DYKE S J.Model-free nonlinear restoring forceidentification forSMA damperswith double Chebyshev polynomials:approach and validation[J].Nonlinear Dynamics,2015,82(3):1-16.

[13]许斌，辛璐璐，贺佳.基于二重切比雪夫多项式的多自由度系统SMA非线性恢复力识别[J].振动与冲击，2014，33(16)：6-13.

[14]许斌，辛璐璐，贺佳.基于切比雪夫多项式模型的多自由度结构非线性恢复力时域识别[J].工程力学，2014，31(11)：99-109.

[15]ANDREW H J.Stochastic process and filtering theory.New York:Academic Press,1970:50-80.

[16]HOSHIYA M,SAITO E.Structural identification by extended Kalman filter[J].JournalofEngineering Mechanics,1984,110(12):1757-1770.

[17]尚久铨.卡尔曼滤波法在结构动态参数估计中的应用[J].地震工程与工程振动，1991(2)：62-72.

[18]YANG J N,LIN S,HUANG H,et al.An adaptive extended Kalman filter for structural damage identification[J].Structural Control & Health Monitoring,2006,13(4):849-867.

[19]YANG J N,PAN S,HUANG H.An adaptive extended Kalman filter for structural damage identifications II:unknown inputs[J].StructuralControl& Health Monitoring,2007,14(3):497-521.

[20]LEI Y,HE M Y.Identification of nonlinear parameters of rubber-bearing in base-isolated building[J].Applied Mechanics&Materials,2012,226-228:1119-1123.

[21]LEI Y,HE M Y,LIN S Z.Model-free identification for nonlinear properties of rubber-bearings in base-isolated buildings[J].Journal of Vibration&Shock,2013,32(20):1-1546.

[22]YING L,HE M Y.Identification of the nonlinear properties of rubber-bearings in base-isolated buildings with limited seismic response data[J].Science China Technological Sciences,2013,56(5):1224-1231.

[23]邓志党，高峰，刘献栋，等.磁流变阻尼器力学模型的研究现状[J]. 振动与冲击，2006，25(3)：121-126.