基于核极限学习机的旋转机械故障诊断方法

王 普，温 峥，高学金，温焕然

（1.北京工业大学 电子信息与控制工程学院，北京 100124；2.数字社区教育部工程研究中心，北京 100124； 3.城市轨道交通北京实验室，北京 100124；4.计算智能与智能系统北京市重点实验室，北京 100124）

随着科学技术的飞速发展，旋转机械在机械、能源、电力、冶金、航空航天和国防军工等行业中得到广泛应用。对旋转机械设备进行故障诊断，既能保证设备安全、可靠运行，又能降低维修成本，延长使用寿命，避免因盲目停机维修而带来的浪费。

旋转机械的故障诊断，主要是通过机器学习模型来处理故障特征与故障模式之间的映射关系，其本质上是对旋转机械振动信号的模式识别过程[1]。目前应用较为广泛的有支持向量机、神经网络等，但这些方法都存在一定的局限性[2-3]。

在目前常用的模式识别方法中，支持向量机（Support Vector Machine，SVM）参数过多而且难以选择，利用粒子群或遗传(Genetic Algorithm，GA)等智能算法优化参数需要消耗大量时间[4]；传统的神经网络学习算法，如BP算法[5]，需要人为设置大量的网络训练参数，它通过局部调整的方法进行改进，容易陷入局部优化，最终导致训练失败。另一方面，由于网络结构模型不单一，神经网络的参数需要迭代调整，训练效率不高，容易陷入过拟合现象；极限学习机(Extreme Learning Machine，ELM)是一种新颖的单隐层前馈神经网络的快速算法，具有参数选择简单、学习速度快、泛化性能好等优点，在很多领域中得到了应用，如文献[6]把ELM方法用在石油储罐罐底腐蚀信号识别中。然而，由于ELM随机产生输入权值和隐含层阈值，导致算法不稳定[7]。核方法由于具有良好的非线性映射能力已经在许多问题上得到应用,其最具有代表性的应用就是SVM。文献[8]中提到，核方法也可以应用于极限学习机算法中，核ELM(Kernel Extreme Learning Machine，KELM)解决了ELM算法随机初始化的问题，KELM方法分类准确率高、推广能力好，具有很高的鲁棒性[9]。本文把KELM应用于旋转机械的故障诊断，提取振动信号的小波能量特征作为故障特征，选择高斯核函数建立KELM模型，获得了比较满意的诊断效果。

1 核极限学习机理论

1.1 极限学习机

ELM是基于单隐层前向神经网络（SLFNs）的模型[10]，它的两个重要优势是：

（1）ELM所有的隐藏节点独立于目标函数或训练数据；

（2）传统的学习方法必须先看见数据才能产生隐含层节点的参数，而ELM不需要。ELM的初始权值随机设置，在训练过程中不需要调整，只需要求解出最小化输出权值即可[11]。

SLFNs的数学模型为

其中：L为隐层节点数，g(∙)为激活函数，βi为连接隐层节点和输出节点的权值向量，ai为连接输入节点和第i个隐层节点的权值向量，bi为第i个隐层节点的阈值。

对于N个学习样本Z=(xi，ti)，i∈ 1,2,…,N，其中xi=(xi1,xi2,…,xi n)T为输入，ti=(ti1,ti2,…,ti n)T为输出，ELM训练方法是：

①确定隐层节点个数L和激活函数g(∙)；

②随机设定输入权值ai和隐层节点阈值bi；

③计算隐层输出矩阵，即

④ 计算输出层权值

其中：H+是H的广义逆，，m是输出状态的个数。

极限学习机模型如图1所示。

图1 极限学习机

1.2 核极限学习机

使用核函数的基本原理是通过非线性函数把输入空间样本数据映射到高维特征空间，然后在高维特征空间进行数据的处理。核函数技术关键在于通过引入核函数，把非线性变换后的高维空间的内积运算转变为原始输入空间中核函数的计算。

在ELM的训练过程中，由于输入权值和隐层节点阈值是随机赋值的，这会导致ELM模型的不稳定。为解决这一问题，将核方法引入ELM中。核函数的引入，不仅解决了稳定性问题，而且计算更为简便。

ELM模型输出为

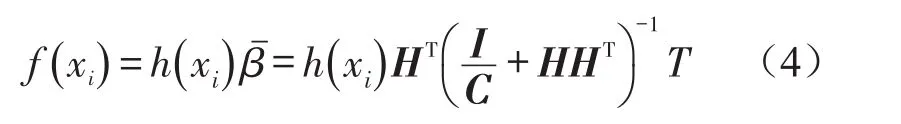
其中：h(xi)=[g(a1,xi+bi)…g(aL,xi+bL)]为隐含层输出，那么隐层输出矩阵H就可表示为

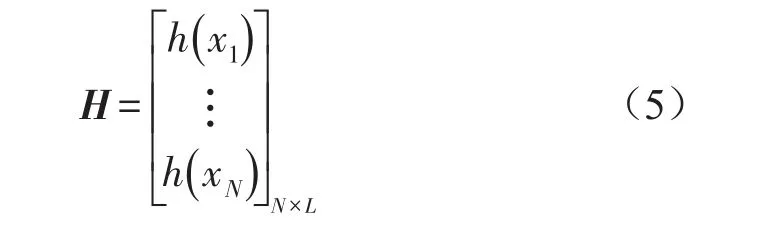
把每一个样本的隐层输出h(xi)都看作是样本xi的非线性映射，于是

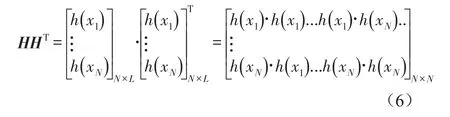
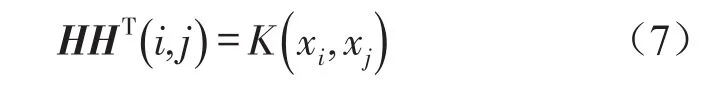
于是有

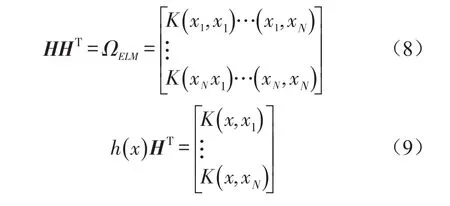
于是KELM模型输出为

由以上推导可知，KELM通过引入核函数将输入样本映射到高维空间，KELM以稳定的核矩阵替代了ELM的随机隐层输出矩阵，在此基础上可求得唯一确定的输出权值，最终得到稳定的预测输出。

2 基于KELM的旋转机械故障诊断

由于随机产生输入权值和隐含层阈值会导致ELM算法不稳定，核函数的引入，即采用KELM算法能够降低诊断模型的不稳定性。

旋转机械在不同故障状态下的振动信号差别较大，对信号进行小波分解后各频带内的能量差异较大，根据各频带能量差异性可以判断旋转机械的故障类型。因此本文采用小波能量方法提取旋转机械的故障特征，作为KELM分类器的输入参数，从而对旋转机械的工作状态进行分类。

旋转机械的故障诊断工作主要分为故障特征提取和故障分类两部分，包括以下几个步骤：

(1)采集旋转机械的振动信号；

(2)将样本分为训练样本和测试样本；

(3)对训练样本和测试样本分别进行信号的预处理，去除信号噪声；

(4)对于去噪后的样本，提取故障特征，并进行归一化处理；

(5)用训练样本的归一化故障特征训练KELM模型，选择核函数求解式（10）得最优分类函数；

(6)将测试样本的归一化故障特征输入训练好的KELM模型，进行故障的分类。

故障诊断过程如图2所示。

图2 旋转机械KELM故障诊断过程

对采集的振动信号进行小波分解，并选用合适的阈值函数对小波系数进行阈值处理，达到去除噪声的效果。以阈值处理后的小波系数为基础，求取信号各频段能量。以7层小波分解为例，7个低频段和1个高频段由低到高依次编号为1,2，…8。

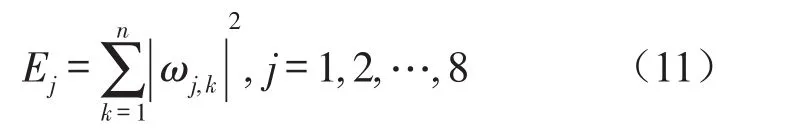
式中：ωj,k表示j尺度下点k处经阈值处理后的小波系数。以各频段小波能量为元素构造特征向量为

T即为旋转机械的故障特征向量。以特征向量T作为KELM分类器的输入，采用训练样本按照式（10）进行模型训练。用训练好的分类器对测试样本进行分类，识别旋转机械的正常状态、转子不平衡故障、转子不对中故障和轴承座松动故障。

3 实验和结果分析

实验在MFS机械故障模拟实验台上进行，实验装置如图3所示。

图3 机械故障模拟实验台

在轴承座上垂直安装加速度传感器测量转子振动信号，NI9234模块和NI9171便携式机箱配合计算机LabVIEW编程进行信号采集。当旋转频率为40 Hz时，以2 kHz采样频率采集正常信号和转子不平衡、转子不对中和轴承座松动3种故障信号，每种信号类型采集60个样本，每个样本含有32 k个采样点。图4是4种状态下前2 048个点的时域波形。在时域图中，直观上并不能看出明显的状态差别。

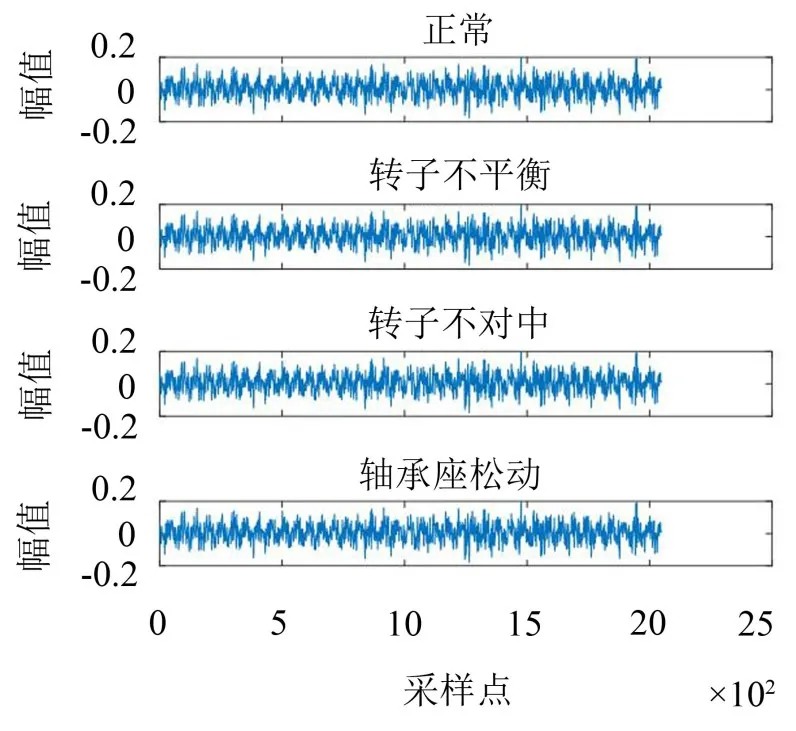
图4 四种振动信号的时域波形

采集的振动信号含有一定的噪声，首先要进行噪声的去除。小波阈值去噪是一种时频域去噪方法，在机械领域有着广泛的应用。小波阈值去噪分为小波分解、阈值处理和小波重构3个步骤。这里选用db5小波进行7层小波分解，采用软阈值处理方法。

信号经小波变换后的能量与原始信号能量等价。旋转机械不同故障状态下的振动信号差别较大，对应的小波分解后各频带内的能量也有所差别，因此可以提取各频带能量作为故障特征。对去噪后的信号进行7层db5小波分解，以7层近似系数和第1层细节系数为基础，进行各频段能量计算，组成8维特征向量。正常样本和3种故障样本的特征向量如图5所示。小波节点1至8分别对应小波分解的从低到高的7层低频段能量和第1层的高频段能量。从图5中可以看出不同类型的振动信号的小波能量特征向量存在明显差别。

把提取出的特征向量进行归一化处理，然后进行故障分类。

在采集的4种振动信号中，选取训练样本各30组，共计120组；测试样本各30组，共计120组。正常状态、转子不平衡故障、转子不对中故障和轴承座松动故障的类别标签分别设为1、2、3、4。

实验中发现ELM算法的诊断结果受隐层节点数的影响很大，为了验证这一结论，实验设定了不同的隐层节点数，连续运行100次ELM算法求得平均准确率，如图6所示。

“一切自在的客体为主体所掌握都要经过主体已有的心智结构(包括已经内化了的知识、观念及思维模式等)的筛选与转换。”换言之,个体素质形成与发展的水平,在很大程度上就取决于个体将周围的精神文化有选择地逐步内化这个过程。对所参照的人格规范及价值体系的内化,决定着个体的理想自我的形成。教育活动中向学生所提出的外部的、客观的知识、规范,只有通过“内化”才能成为学习主体内部的知识和规范。考察职业院校学生责任文化素质形成的过程,其内化是一个由认知转化、知能转化、知行转化相辅相成的综合统一、反复交错的动态开放系统。

从图6中可以看出，ELM算法的平均准确率的确随着隐层节点数的变化有很大的变动，当隐层节点数设为7时，ELM诊断准确率达到了最大值93.28%。

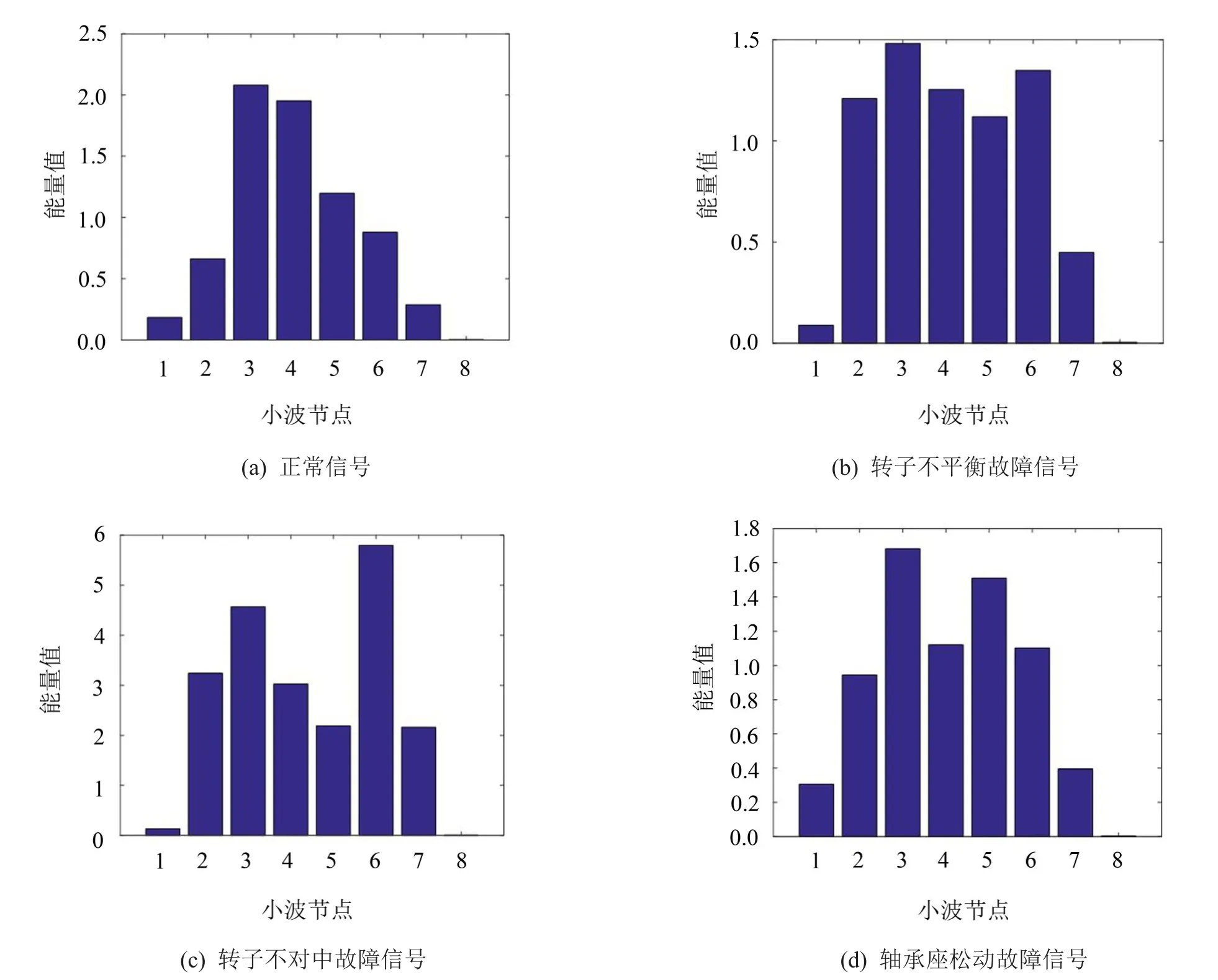
图5 信号的小波能量特征

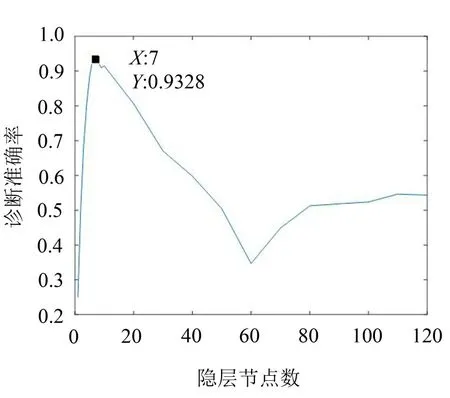
图6 ELM算法诊断准确率随隐层节点数变化情况

由于随机初始化输入权值和隐层节点阈值，会导致ELM算法的不稳定性。实验对KELM算法和ELM算法的稳定性进行了对比，如图7所示。其中KELM的核函数为高斯核函数，核半径设为0.5；ELM激活函数类型为“Sigmoid”函数，隐层节点数设为7，两种算法各执行了100次。

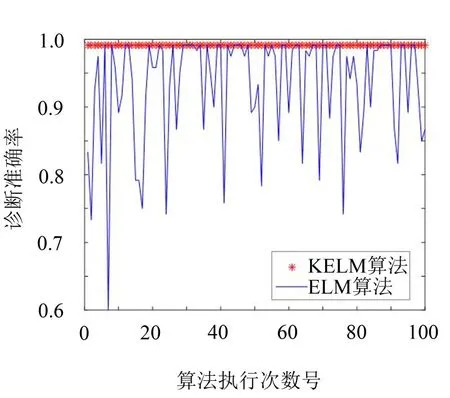
图7 KELM和ELM算法稳定性对比(隐层节点数为7)

从图7可以看出，ELM算法分类准确率的随机性很强，算法学习性能不稳定；而KELM中用核映射代替了ELM中的随机映射，解决了ELM算法的诊断不稳定问题，诊断精度不随算法执行次数的变化而波动，稳定性增强。

最后进行KELM诊断，并与SVM进行对比，其中KELM的核函数仍然选为高斯核函数，核半径设为0.5；SVM选用高斯核函数。KELM的诊断结果如图8所示，SVM诊断结果如图9所示。

图中红色*型代表测试样本的实际类别，蓝色o型代表测试样本的预测类别，若红色和蓝色重合则表示诊断正确，否则诊断错误。

从图中8可以看出，KELM算法的故障诊断，对于4种类别的120个测试样本，只在类别3即转子不对中故障处出现一处诊断错误，KELM的诊断准确率较高，优于SVM。

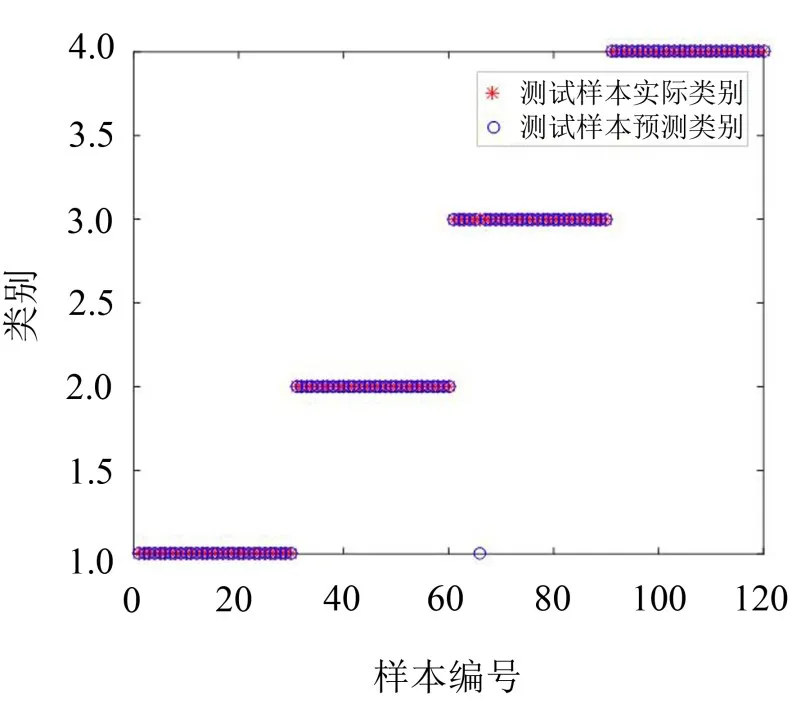
图8 KELM故障诊断结果

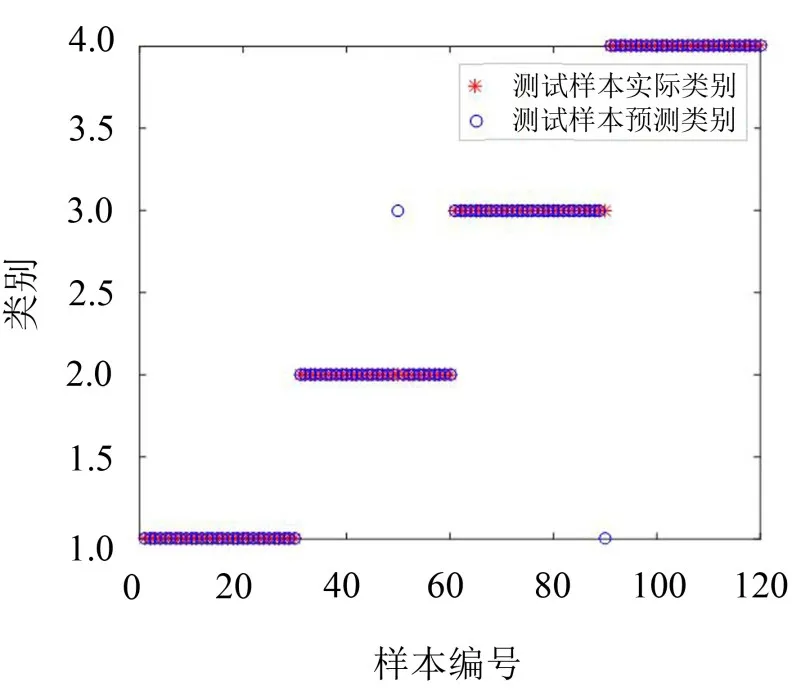
图9 SVM故障诊断结果

KELM和SVM的诊断准确率和耗时对比如表1所示。

表1 KELM和SVM的诊断结果对比

从表1中可以看出，KELM算法在诊断准确率上要高于SVM，同时在耗时上存在优势，因此该方法在旋转机械故障诊断中效果更好。

4 结语

把KELM应用于旋转机械的故障诊断，提取振动信号的小波能量作为故障特征，选择高斯核函数建立KELM模型，获得了比较满意的诊断效果。KELM中核函数的引入，避免了ELM随机初始化造成的模型不稳定问题，与ELM和SVM的对比结果表明，KELM是一种诊断准确率高、稳定性好的旋转机械故障诊断方法。

参考文献：

[1]温熙森.模式识别与状态监控［M］.北京：科学出版社，2007.

[2]WANG HUA QING,CHEN PENG.Intelligent diagnosis method for rolling element bearing faults using possibility theory and neural network[J].Computer＆Industrial Engineering,2011,60(4):511-518.

[3]FEI SHENG WEI,ZHANG XIAO BIN.Fault diagnosis of power transformer based on support vector machine with genetic algorithm[J].Expert Systems with Applications,2009,36(8):11352-11357.

[4]李兵，张培林，任国全，等．运用EMD和GA_SVM的齿轮故障特征提取与选择[J]．振动测试与诊断，2009，29(4)：445-448.

[5]RUMELHART D E,HINTON G E,WILLIAMS R J.Learning internal representations by error propagation[M].USA:MIT Press,1986.

[6]李一博，祝慧宇，张玉祥，等.基于极限学习机和b值法的罐底声发射检测腐蚀信号识别方法[J].振动与冲击，2015，34(11)：35-40.

[7]HUANG GUANG BIN,ZHOU QIN YU,SIEW C K.Extreme learning machine:Theory and applications[J].Neurocomputing,2006,70(1/2/3):489-501.

[8]HUANG G B,ZHOU H,DING X,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics,2012,42(2),513-529.

[9]陈紹伟，柳光峰，冶帅.基于核极限学习机的模拟电路故障诊断研究[J].西北工业大学学报，2015，33(2)：290-294.

[10]YANG YI MIN,WANG YAO NAN,YUAN XIAOFANG.Bidirectional extreme learning machine for regression problems and its learning effectiveness[J].IEEE Transactions on Neural Networks,2012,23(9):1498-1505.

[11]HUANG GUANG BIN,ZHU QIN YU,SIEW C K.Extreme learning machine:A new learning scheme of feed forward neural networks[C]//Proceedings of International Joint Conference on Neural Networks(IJCNN).Budapest,Hungary:IEEE Press,2004:985-990.