粗轧电机磁流变悬置性能研究

苏锦涛，段绪伟

(1.中国汽车工程研究院股份有限公司，重庆 401122；2.重庆大学机械传动国家重点实验室，重庆 400030)

0 前言

随着重工业的发展，大功率、低转速粗轧电机在轧机设备上应用越来广泛，伴随着大功率的电机噪声、振动问题一直是重型机械冶金领域的难题。粗轧电机悬置作为动力源的隔振系统，对降低振动和噪声起着至关重要的作用。为了控制电机的低转速波动往往需要对隔振系统进行设计，对于控制低转速的波动，悬置系统的大阻尼特性具有显著作用，而对于电机高频不平衡力所引起的振动激励，则建议悬置系统具有小阻尼特性，因此，设计电机悬置系统隔振原件十分必要。本文提出解耦膜式磁流变悬置系统，对悬置结构、状态方程、性能参数、参数模型仿真进行了相关研究。[1-7]

1 基本结构

磁流变悬置的阻尼特性具有可变性，阻尼与外界磁场的磁通量具有相关性，通过改变外界磁场的磁通量改变液体的流量，从而影响悬置结构的阻尼特性。在外部磁场激励作用时悬置内部的液体由液态转变为液态、固态耦合状态，呈现可控的屈服强度[8]。

考虑到悬置系统的磁流变特性，设计了阻尼可调的磁流变悬置[9,10]。本文设计的磁流变悬置结构如图1所示。该磁流变悬置主要由橡胶主簧、液室、磁芯、线圈、液体通道、橡胶底膜、传感器、解耦膜等结构组成。

电机低频激励时，悬置的上液室体积容量产生变化，磁流变液体流经可变阻尼通道，根据悬置主动端的振动情况改变电流大小，从而实现磁通量的改变。调节液体通道的的流阻，可调节悬置的阻尼特性。电机高频高频激振时，液体流经阻尼通道增大了液体能量损失[11]，从而控制高频振动特性。

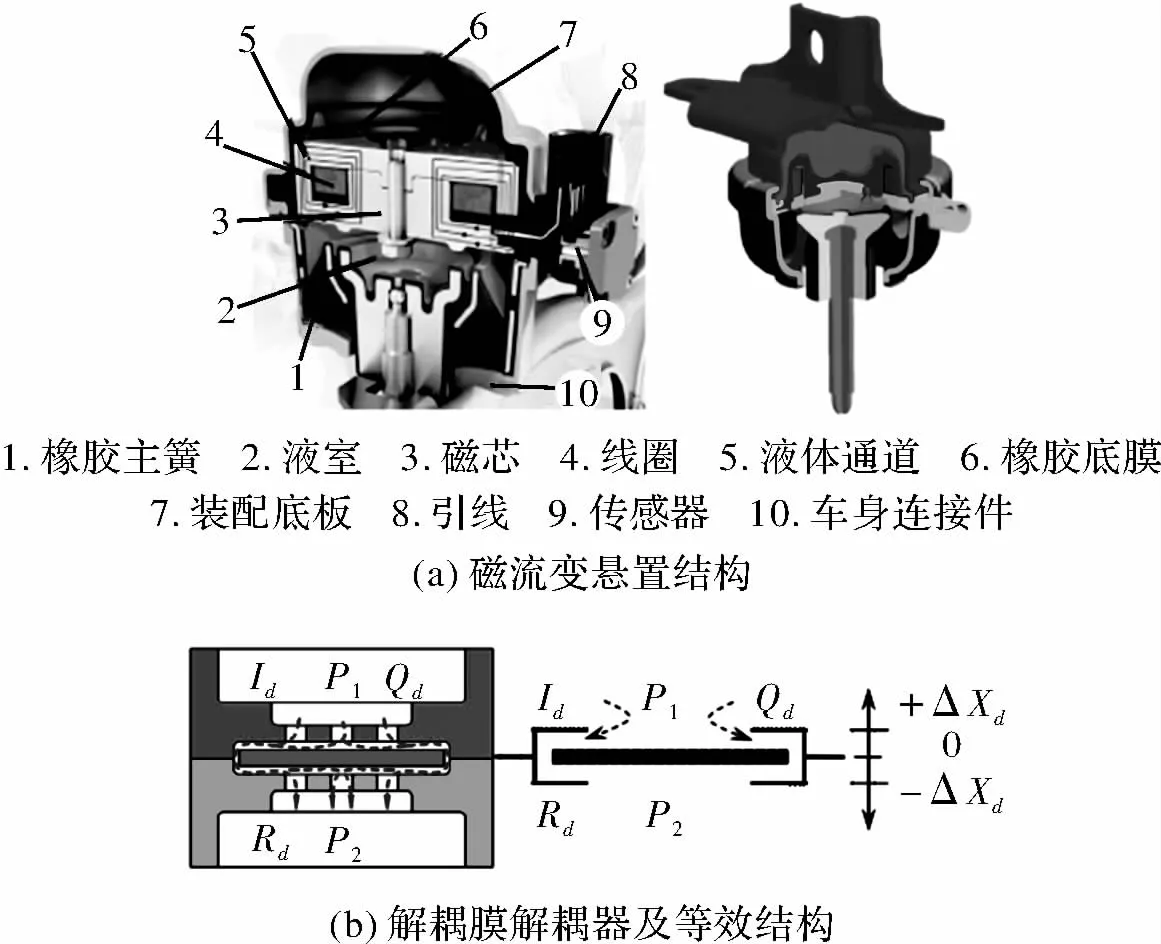
图1 磁流变悬置结构、解耦膜结构示意图

2 基本模型

2.1 参数模型

悬置的参数模型如图2所示。

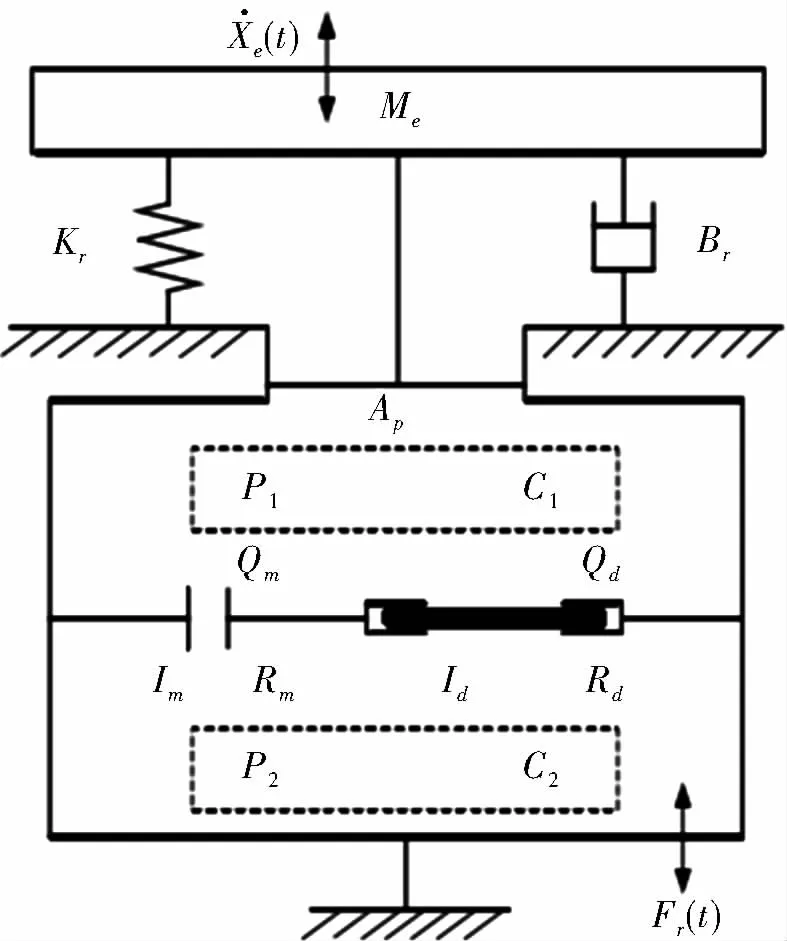
图2 悬置参数模型

图2中Kr构成了弹簧系统的刚度参数，K、B两个参数构成主要弹簧的刚度、阻尼系统。参数C是悬置模型的体积刚度，参数A为可变面积，工作模式及原理是通过调节阻尼通道的孔径控制液体的流量。解耦膜的流量变化量、节流盘液体的流量变化量分别控制上液室和下液室的面积大小，从而控制流量，改变作用力。悬置模型中的控制量包括输入激励X(t)和悬置传递力F(t)。

2.2 键合图结构

键合图结构是在1950年由Paynter H教授提出，后由Karnopp D.C和Rosenberg R.C等根据统计能量的理论得出的一种能量化、模块化的一种复杂学科的动态分析方法，由于该方法直观，流程化因此在磁流变悬置的设计上得到了广泛的应用[12]。该理论根据能量守恒，将机械能、电能、热能、电磁能等物理量归纳为势能e(t)、动量p(t)、位移q(t)、流量f(t)等几种变量，并根据系统和子系统的关系，将系统分成若干子系统，以传递图形的方式进行表达。根据键合图结构，得到磁流变悬置的键合图模型[13]，如图3所示。

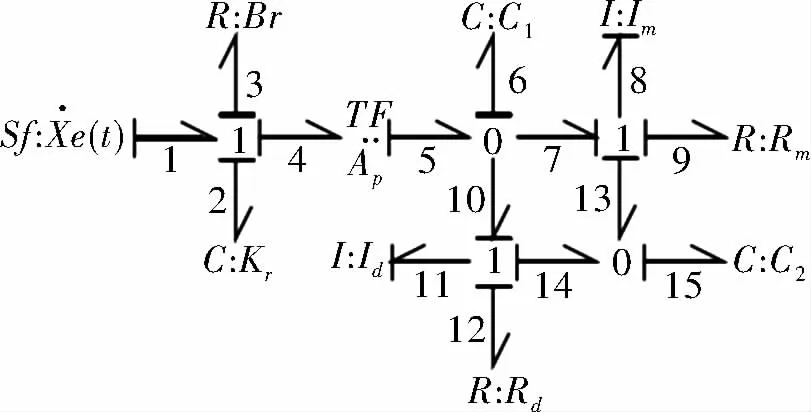
图3 键合图模型

根据键合图结构理论，液室体积刚度的非线性可作简化[14]，本文只考虑磁流变液屈服极限与磁通量强度的非线性，即磁流变液阻与磁流变液屈服极限的非线性函数，磁流变可变流量的液阻表示为:Rm=Rm0+Rτ(τy(B))，可推导出磁流变悬置的动态方程如下：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

将各式进行拉式变换，推导得出磁流变悬置刚度为

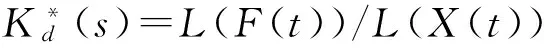
(8)

其中，

相关系数ai、bi、ci和di(i=0,1,2,3,4,5)可以由集总参数表示。令s=jω，则有

(9)

式中，K1为系统储能刚度；K2为系统损失刚度。

3 液阻特性

为了得出磁流变悬置的非线性液阻Rm，本文运用有限元法电液耦合法则对其辨识。在不同电流激励下，对磁流变磁感应强度、磁通量进行有限元计算，再利用液阻计算式进行识别。磁流变悬置的磁芯结构尺寸参数标注如图4所示。可推导出非线性液阻Rm的计算式为

(10)

式中，Qm代表磁流变悬置的液体流量。ρ为磁流变悬置液体密度；τy为磁流变液的屈服应力。

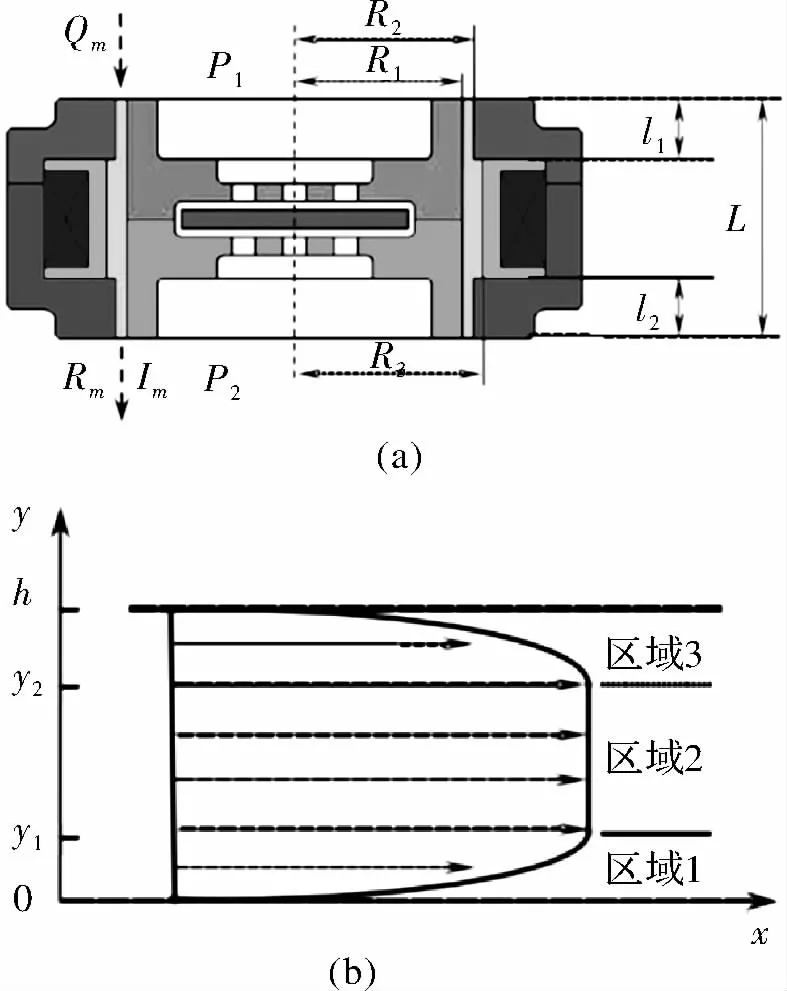
图4 悬置磁芯组件结构

应用有限元软件建立悬置的磁芯组件、磁流变液的固液耦合模型，磁芯组件用2维单元，磁流变液体用一维单元模拟，在模型磁芯线圈位置加载电流密度激励，在磁场的作用下，即可获得磁流变液体的磁通量和感应密度。激励电流允许值2.0 A时，磁芯部分磁场强度分布如图5所示。

根据公式(10)液阻Rm的计算公式，以及磁感应强度、激励电流，可获得液阻Rm与激励电流之间的正相关曲线，如图6所示。

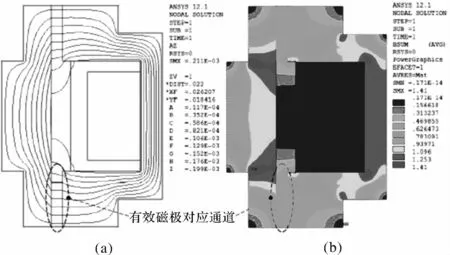
图5 激励电流为2.0A时，磁场强度分布云图

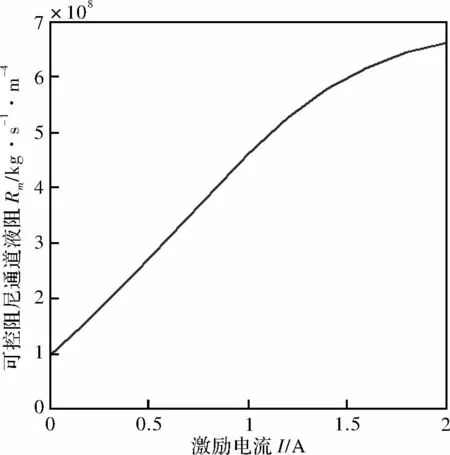
图6 液阻Rm电流关系曲线

悬置参数中其余参数可利用固液耦合、电磁耦合方法进行辨识，文献[4,5,14]中均有介绍。辨识的悬置参数如表1所示。

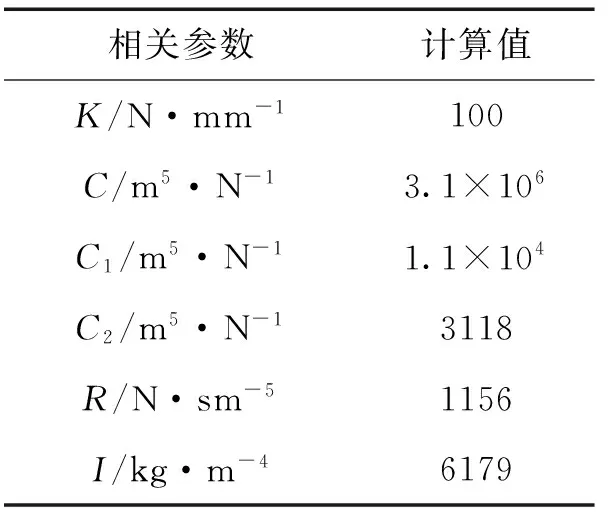
表1 悬置相关参数

4 动态特性

4.1 低频激励

低频激励时，磁流变液体由下解耦膜游离到上解耦膜，在下解耦膜处被液体隔板阻断，只有小部分液体流经上解耦膜，对动态方程进行简化，结合电耦合仿真结果，可获得非线性模型随激励电流变化的低频特性曲线，如图7、图8所示。

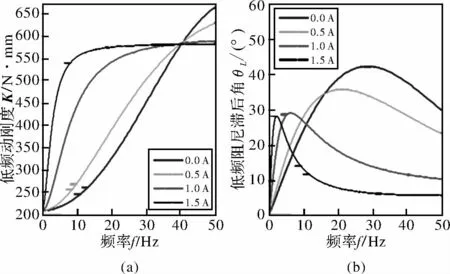
图7 刚度、滞后角曲线

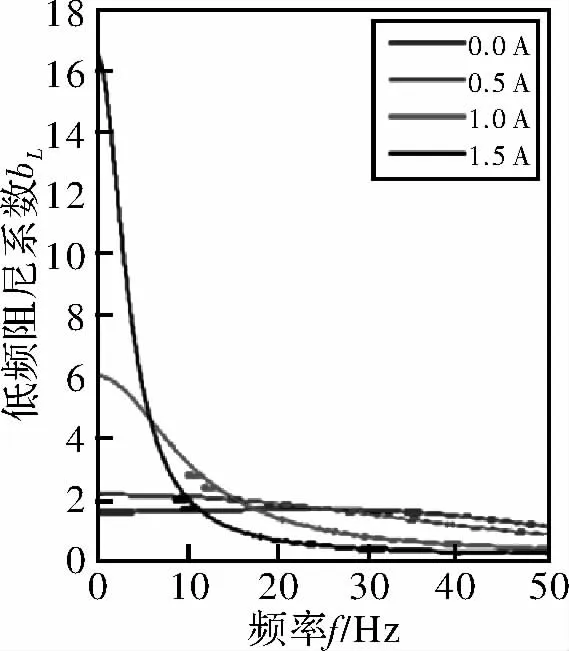
图8 阻尼系数

由曲线结果可知，低频激励，磁流变悬置的动刚度曲线可知，不同的电流激励下随着频率的增加，磁流变悬置的动刚度曲线变化不同，电流为0～0.5 A区间，随着激励频率的增加，结构的动刚度值不断增加，最高值为650 N/mm。激励电流在1～1.5 A区间，随着激励频率的增加，结构的动刚度值趋于稳定值，稳定值为550 N/mm。由磁流变悬置的阻尼角曲线可知，不同电流激励对于阻尼角的控制有所不同，在电流激励为1.0～1.5 A时阻尼角对于隔离低频的振动具有一定的作用，阻尼角峰值频率为5 Hz，电流激励0～0.5 A时阻尼角在30 Hz，因此可以通过磁流变悬置的电流控制低频不同频率的阻尼特性，具有分布控制的作用。

4.2 高频激励

高频激振时，磁流变液体流经解耦膜，通过解耦膜中的可变体积腔体实现液态阻尼作用，磁流变悬置模型高频动特性曲线，如图9和图10所示。高频激励下，磁流变悬置的动刚度随着激励频率的增加呈现先增大后减小的趋势，频率在50～70 Hz区间，动刚度随激励的频率增大，激励频率在70～205 Hz区间，动刚度与激励频率负相关，达极小值240 N/mm；

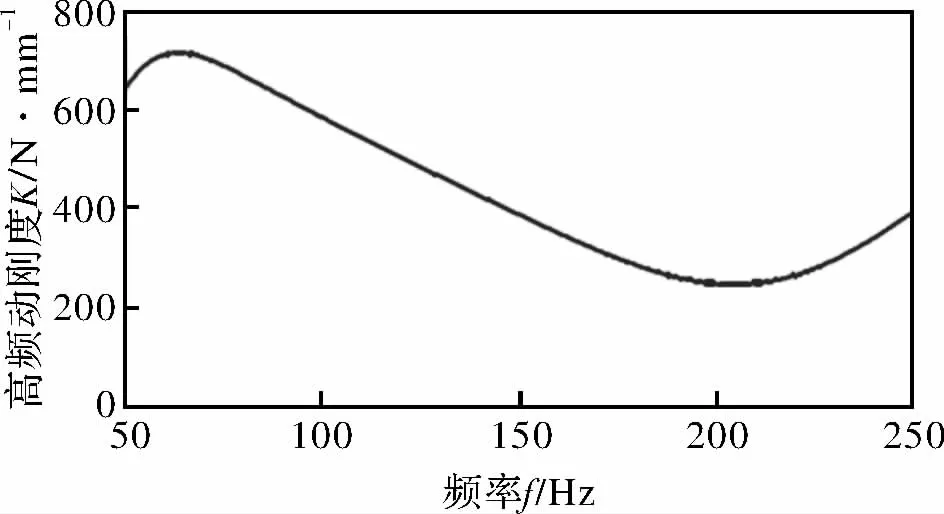
图9 高频动刚度曲线

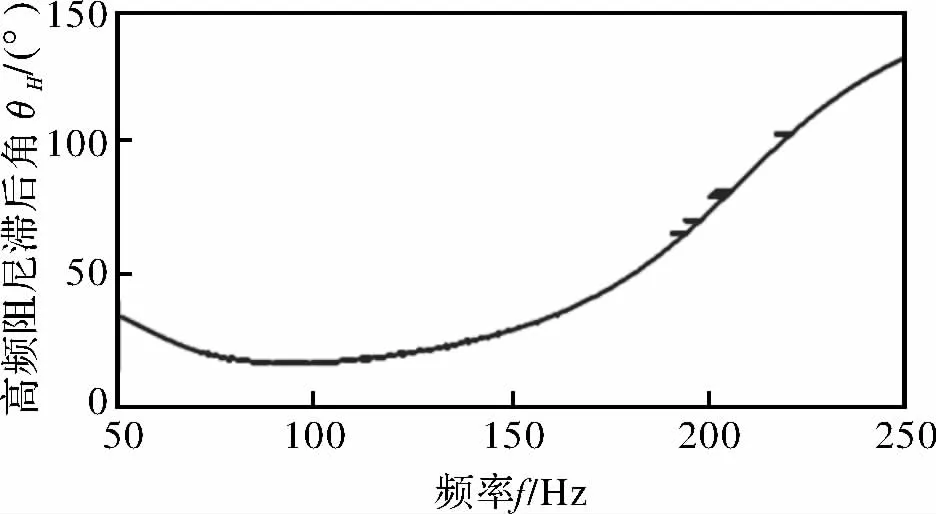
图10 高频阻尼角曲线

由悬置高频阻尼角结果可知，阻尼角随激励频率增大而升高，激励频率在250 Hz时阻尼角出现最大峰值131.9°，高频激励主要控制阻尼角的高频范围，与动刚度曲线的结构可知，高频激励下可以通过调节激励电流，从而改变悬置的动刚度和阻尼角。

5 结束语

本文建立了粗轧电机磁流变悬置的力学模型，并对悬置的高、低频动态特进行了分析，分析结果表明：低频激励作用下电流值为1～1.5 A时，磁流变悬置具有良好的阻尼特性，阻尼峰为5 Hz，对隔离低频大振幅振动具有良好的效果。电流值为0～0.5 A激励作用下阻尼峰为30 Hz，对于隔离中低频振动具有一定的效果，可以根据不同的工况选择不同的隔振阻尼峰值；高频激励时，磁流变悬置动刚度具有宽阔的频带特性，可调节的区间较为广泛，阻尼角为250 Hz,对于隔离高频也具有一定的作用。

参考文献:

[1] Y.Yu, N.G.Naganathan, R.V.Dukkipati. A literature review of automobile engine mounting systems[J]. Mechanism and Machine Theory, 2001,36(01): 123-142.

[2] Jun Hwa Lee, Rajendra Singh. Critical analysis of analogous mechanical models used to describe hydraulic engine mounts[J]. Journal of Sound and Vibration, 2008,311(03-05):1457-1464.

[3] Thanh Quoc Truong, Kyoung Kwan Ahn. A new type of semi-active hydraulic engine mount using controllable area of inertia track [J]. Journal of Sound and Vibration, 2010,329(01):247-260.

[4] 张云侠. 液阻悬置动态特性仿真与试验研究[D]. 上海：上海交通大学,2007.

[5] 李堑. 汽车发动机液阻悬置动态特性与参数辨识研究[D]. 上海：上海交通大学,2007.

[6] Vahdati Nader, Saunders L, Ken Lauderbaugh. High frequency testing of rubber mounts[J]. ISA Transactions,2002,41(02):145-154.

[7] M. Farid Golnaraghi, G. Nakhaie Jazar. Development and Analysis of a Simplified Nonlinear Model of a Hydraulic Engine Mount [J]. Journal of Vibration and Control, 2001(07):495-526.

[8] Nguyen, T. M., Ciocanel, C., Elahinia, M. H. A. squeeze-flow mode magnetorheological mount: design, modeling, and experimental evaluation[J]. Journal of Vibration and Acoustics, 2012,134(02): 1-11.

[9] Janusz Golfdsz, Bogdan Sapinski. Modeling of magnetorheologi-cal mounts in various operation modes[J]. Acta Mechanica et Automatica,2011,5(04):29-39

[10] 胡勇. 汽车发动机磁流变悬置研究[D]. 重庆：重庆大学,2008.

[11] 范让林,吕振华，刘立，等. 液阻悬置节流盘的作用机理[J]. 工程力学，2009,26(03):229-233.

[12] 王中双. 键合图理论及其在系统动力学中的应用[M]. 哈尔滨:哈尔滨工程大学出版社,2007.

[13] 张云侠，张建武，上官文斌，等. 新型发动机被动液阻悬置动态特性分析[J]. 上海交通大学学报，2006,40(06):942-946.

[14] G.KIM , R.SINGH. A study of passive and adaptive hydraulic engine mount systems with emphasis on non-linear characteristics [J]. Journal of Sound and Vibration.1995,179(03):427-453.