改进的灰色模型在流动人口预测中的应用

郭雪峰，黄健元，王 欢

（河海大学a.理学院；b.公共管理学院，南京 211100）

0 引言

流动人口预测是政府实际管理决策中的基础工作。进入21世纪以来，南京市经济社会环境发生了深刻变化。特别是“十二五”期间，南京市经济结构调整、产业结构升级、城市空间格局优化、基础设施建设完善、社会保障加强等，改变了人口流动的社会、经济与人文环境。在这些因素的共同作用下，全面把握南京市流动人口的性质、特征、演进趋势，是促进南京成为长三角地区副中心城市、促进经济社会进一步发展所必须具备的基础。因此，对南京市流动人口的变动趋势进行准确预测具有重要的现实意义。

人口预测模型目前主要有：因素分析法、时间序列预测模型、神经网络预测模型等。从应用角度来看，因素分析法中各因素的确定和预测就相当困难，而且各因素之间会出现共线性问题，会影响预测的准确度，可信度将大大降低。由于事物的发展不仅在时间上有连续性，而且随着市场现象的发展会出现一些新特点，事物发展的复杂多样性会影响时间序列预测模型的准确性。神经网络预测模型会由于信息量的缺少导致预测精度不高。灰色预测模型是通过对部分已知信息的生成、开发去认识现实世界，正确掌握和描述系统运行行为和演化规律的方法，具有较强的适用性，用灰色系统的预测模型对信息量较少的问题进行研究有很大发展空间。

传统的灰色预测模型对于流动人口影响因素的不确定性和特殊性，导致流动人口的预测结果误差变大，因此，针对这些问题本文采用自适应滤波法的残差修正思路，对传统灰色预测模型进行了进一步修正，以期能提升灰色预测模型在流动人口预测方面的精度，为流动人口的统筹管理提供科学的数据支持。

1 南京市流动人口现状

1.1 流动人口规模

人口流动已经成为当前我国经济社会发展的重要阶段性特征。本文对流动人口的定义即人口不在其户籍所在常住地活动。根据南京市2000年、2010年南京市人口普查数据及2015年1%人口抽样调查数据统计，2015年南京市流动人口规模达到198.57万人，占南京市常住人口的24.13%。其中：省内流动人口102.01万人，省外流动人口96.56万人。2000—2010年是南京市流动人口快速增长的阶段，10年内南京市的流动人口总量增长了111.68万，年均增长率为9.17%。但是，进入2010年以来南京市流动人口的增长速度有明显的放缓，2010—2015年南京市流动人口仅增加了7.31万人，年均增长率仅为0.75%。从2000年到2015年南京市流动人口数量变化情况看，流动人口总量上呈现出从“快速增长”到“缓慢增长”的变动趋势。其中：省内流动人口从2000年的40.59万人快速增加到2010年的104.51万人，但2015年省内流动人口数量上略低于2010年；省外流动人口从2000年的38.98万人持续增长至2015年的96.56万人。

1.2 流动人口性别、年龄结构和受教育程度

2015年南京市流动人口中男性为101.45万人，女性为97.13万人，男女性别比为1.04,流动人口总体上男性略多于女性，差别不大。2015年南京市流动人口年龄结构中，0～14岁少年儿童人口占总流动人口的4.02%，其中男女性别比为1.15；15～64岁劳动年龄人口占总流动人口的93.99%，其中男女性别比为1.04；65岁及以上老年人口占总流动人口的1.99%，其中男女性别比为1.05。南京市流动人口中以劳动年龄人口为主，各年龄段的性别比差别不大，跟总体基本保持一致。2015年南京市流动人口中小学及以下文化程度的流动人口占比为7.94%，中学及中职流动人口占比为37.11%，而大学专科及以上的流动人口占比为54.95%，整体来看南京市流动人口中受教育程度普遍较高。具体情况见表1。

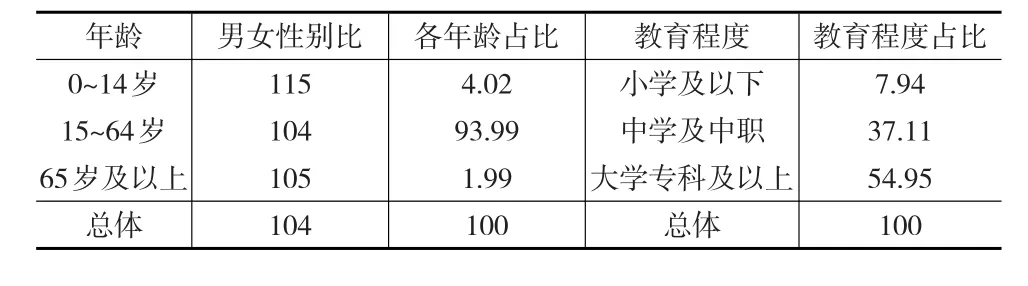
表1 2015年南京市流动人口性别、年龄结构和受教育程度情况 （单位：%）

2 改进的灰色预测模型构建

本文主要对局部地区的流动人口进行预测，传统的灰色预测模型的时间响应函数是指数函数，增长很快，预测值一般偏高，而且容易受外部因素的控制与干扰，会导致灰色模型的直接预测结果差强人意。残差修正的方法有很多，如AM法比较固化、不能根据时间的变化对权数进行动态修正。而自适应滤波法是以历史观测值为基础，进行某种加权预测的方法。它有两个优点：一是技术比较简单，可根据预测意图来选择权数的个数和学习常数，以控制预测，也可以由计算机自动选定。二是它不仅使用了全部历史信息来寻求最优权数，而且随数据轨迹的变化而不断更新权数，从而不断改进预测。因此本文提出了基于自适应滤波法残差修正的灰色预测模型对南京市流动人口预测分析。

2.1 灰色预测模型构建

灰色预测即利用灰色系统所做的预测。所谓灰色系统是介于信息完全已知和信息完全未知之间的过渡系统，它通过对部分已知信息的生成、开发去认识现实世界，正确掌握和描述系统运行行为和演化规律。一般来说，像社会系统、经济系统、生态系统都是灰色系统。

灰色预测的类型有数列预测、灾变预测、系统预测和拓扑预测。常用的模型为灰色GM（1,1）预测模型，建模过程如下：

GM（1,1）是一阶线性微分方程，形式是：

设非负原始序列为 x0={x0(1)，x0(2)，...，x0(n)}，x0作一次累加得，其中

x0(k)的GM（1,1）的微分方程可改为a、u为待定参数，将上式离散化得：Δ1(x1(k+1))+az1(x(k+1))=u，Δ1(x1(k+1))为 x1在k+1时刻的累减生成序列，在k+1时刻x的值。

又因为：

所以：

展开得：

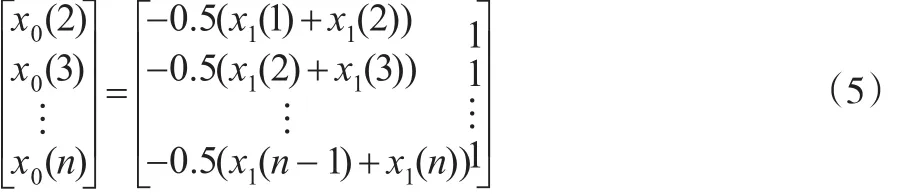
令：

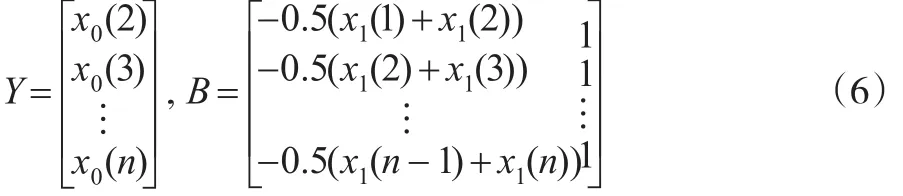
设ϕ=[a，u]T为参数向量，则可得：Y=ϕB。ϕ采用最小二乘法求取，即，从而求得离散解为，还原到原始数据得：

公式（7）即为GM（1,1）灰色预测的具体计算公式。

2.2 自适应滤波法预测模型构建

自适应滤波法是一种以历史时间观测值为基础，进行某种加权预测的方法，“最优”权数的确定是该方法的重点，首先确定一组初始的权数，根据初始权数计算一个预测值，接着计算预测值的误差，最后根据预测误差调整权数使误差减小。这样反复进行，直到找出一组“最优”权数，使得误差达到最小值。由于这种调整权数的过程与通讯工程中的传输噪声过滤过程极为相似，故称为自适应滤波法。自适应滤波法的基本预测公式为：

其中i=1，2，…，N ，t=N，N+1，…，n，n为序列数据的个数，wi为调整前的第i个权数为调整后的第i个权数，k为学习常数，ei+1为i+1期的预测误差。式（9）表示：调整后的一组权数应等于旧的一组权数加上误差调整项，这个调整项包括原观测值、预测误差和学习常数等三个指标。其中权数调整的速度由学习常数k的大小决定。

在调整权数之前，首先要确定学习常数k及权数的个数N。一般来说，当历史观测值随时间呈季节变动时，N取季节性长度值，当序列以一年为周期进行季节变动时，如果数据是月度的，则取N为12；如果季节是季度的，则取N为4；如果历史观测值随时间无明显的周期变动，则可用自相关系数法来确定，即令最高自相关系数的滞后时期数为N。k的取值一般情况下可定为1/N，也可以用不同的k值进行计算，以寻找到一个能使误差最小的k值。初始权数的确定也相当重要，一般可用1/N作为初始权数，即：

2.3 自适应滤波法残差修正的灰色模型构建

首先建立流动人口的GM（1,1）预测模型，其次计算GM（1,1）模型预测值和原始值的残差，再次用自适应滤波法对残差进行预测，最后根据残差预测值对GM（1,1）模型预测结果进行修正。构建基于自适应滤波法残差修正的灰色模型的具体步骤如下：

（1）首先对原始数列做一次累加生成，进而建立灰色GM（1,1）预测模型，由式（7）得出灰色预测结果

（2）根据GM（1,1）模型预测出的序列，计算模拟值的残差序列ε(i)，公式如下：

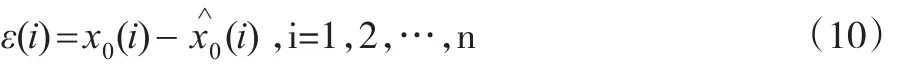
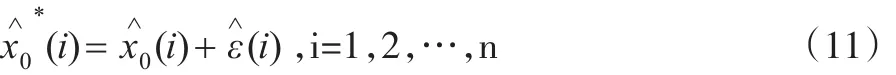
3 改进的模型在南京市流动人口预测中的运用

3.1 数据来源及补充

为验证基于自适应滤波法残差修正的灰色模型的正确性和可靠性，根据2000年和2010年南京市人口普查数据及2015年南京市1%人口抽样调查数据汇总，对南京市流动人口的历史数据（见表2）进行预测分析。

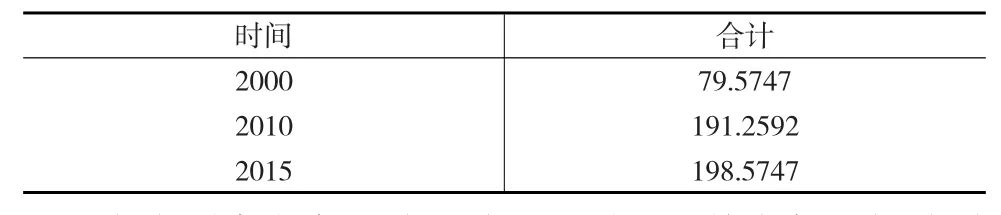
表2 南京市流动人口数据 (单位:万人)

考虑到南京市迁移流动人口增长的特点与生物种群发展具有一定的相似性，在对南京市流动人口进行预测时，首先采用logistic曲线拟合法对2000—2015年的流动人口数据进行补充。

设定初始年份t0=1985，则拟合后的logistic模型为：

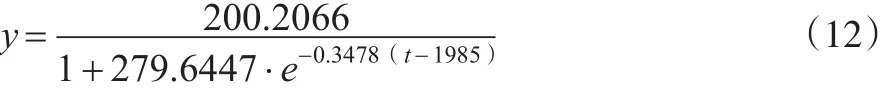
模型参数 L=200.2066，α=279.6447，β=0.3478，模型确定性系数为0.99，模型拟合效果很好，见图1。

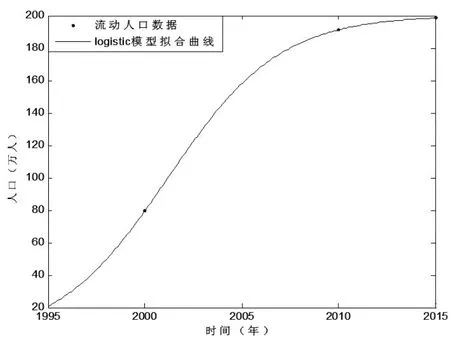
图1 南京市流动人口总量logistic模型拟合效果

Logistic模型下，2000—2015年南京市流动人口总量补充后的数据结果如表3所示。

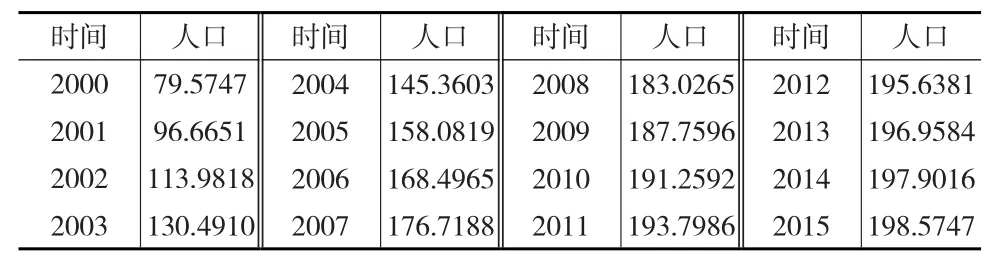
表3 南京市流动人口总量logistic模型补充后数据结果 (单位:万人)

3.2 基于传统灰色模型的预测

以补充后的南京市流动人口总量数据为基础，利用MATLAB软件编程建立灰色GM（1,1）预测模型，得到参数。进而得到GM（1,1）灰色预测模型的公式如下：

通过式（13）可计算出预测结果（见表4），通过传统灰色模型预测的结果分析可知残差较大，其中最大误差高达31.656万人，因此传统的灰色模型预测精度不高，需对模型进行残差修正，即用自适应滤波法对残差预测修正。

3.3 基于改进模型的预测

通过自适应滤波法对表4中残差序列预测，设初始权数的个数N为2，学习常数k为0.5，利用MATLAB软件编程计算出残差预测值（见下页表5）。根据式（11）得到改进后的模型预测值（见表5）。

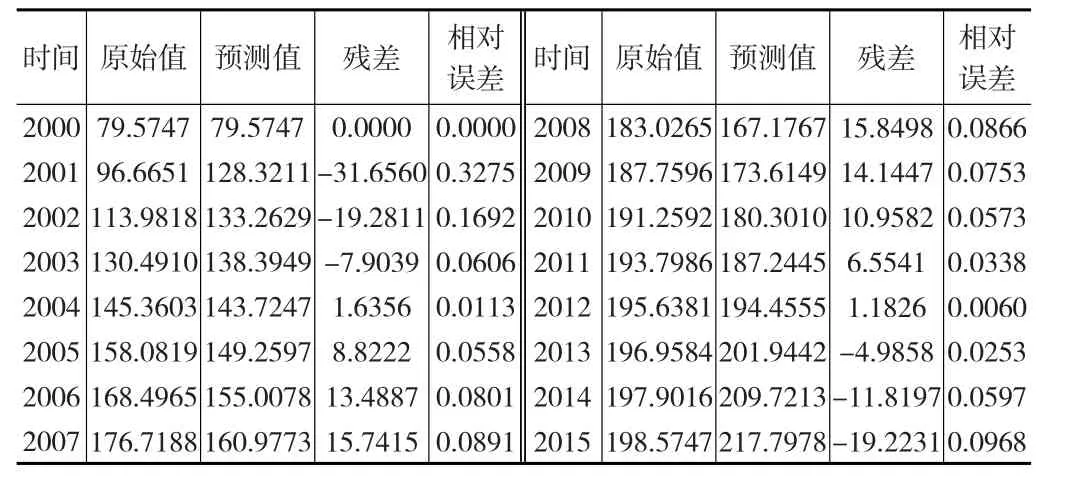
表4 GM（1,1）灰色预测模型的结果分析

表5 残差预测和改进后模型预测结果

3.4 模型结果比较

改进后的模型得出的预测值和只用灰色GM（1,1）模型得出的预测值进行比较，比较结果见表6。

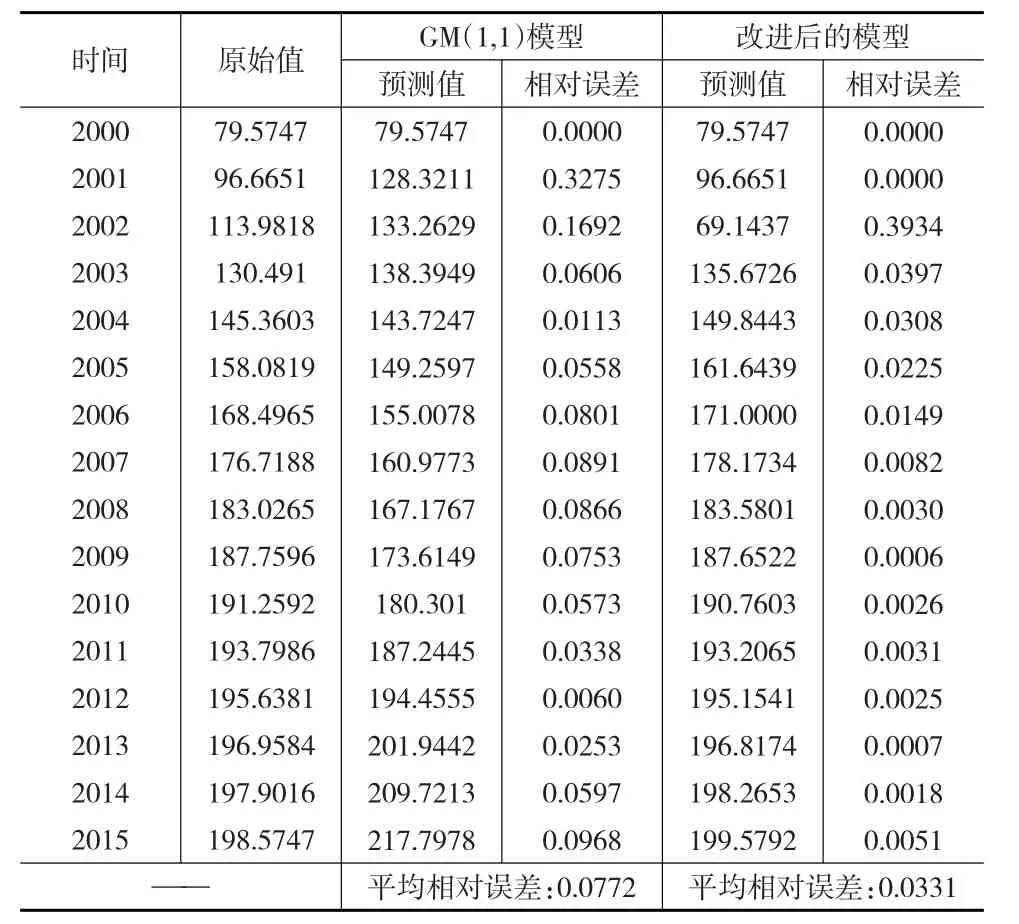
表6 GM（1,1）和改进后模型预测结果比较

由表6可知南京市流动人口总量用GM（1,1）模型预测结果的平均相对误差为0.0772，而采用自适应滤波法残差修正的灰色改进模型预测结果的平均相对误差仅为0.0331，精确度提高了4%，因此改进后的模型预测精度更高。

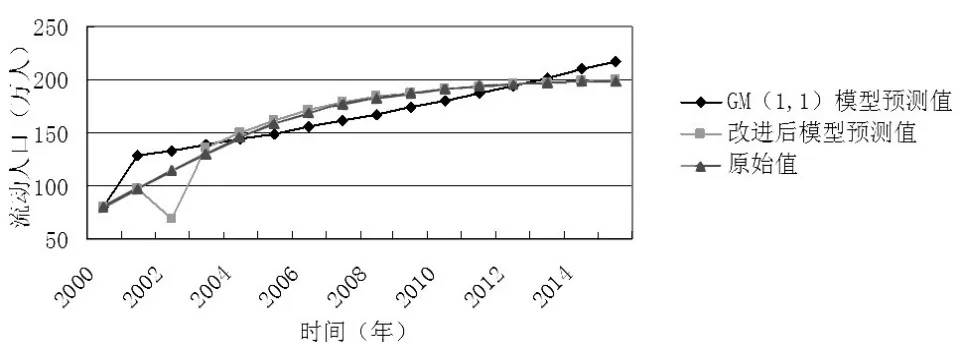
图2 南京市流动人口模型预测结果比较

通过图2也能看出改进后的模型比灰色GM（1,1）模型预测的结果更加接近原始值，说明基于自适应滤波法残差修正的灰色模型比GM（1,1）模型预测的精度更高。传统的灰色GM（1,1）模型呈现指数型增长趋势，使用该模型进行预测时，往往要求事物的发展规律与之保持一致，否则得到的预测结果精度不高。而基于自适应滤波法残差修正的灰色模型利用残差预测对结果修正，不但使预测结果更加接近事物本来的发展规律，而且能够在保持一定精度的情况下，对指数型增长之外的事物预测。因此，基于自适应滤波法残差修正的灰色模型在提升预测精度的同时又增加了模型的适用性。

利用基于自适应滤波法残差修正的灰色模型对南京市2016—2020年的流动人口数量进行预测，结果如表7所示。

表7 改进后模型预测结果 (单位:万人)

4 结论与讨论

本文主要分析了南京市的流动人口现状，并在传统的灰色GM（1,1）模型基础上，构建基于自适应滤波法残差修正的灰色模型，通过南京市的流动人口历史数据来比较改进后的模型和传统的模型预测精度，并预测了南京市流动人口未来几年的变化趋势。

主要结论有：进入21世纪以来，南京市流动人口数量呈现先快后慢的增长趋势，增速趋缓。南京市流动人口中以劳动年龄人口为主，各年龄段的性别比差别不大，整体上受教育程度较高。通过对比验证基于自适应滤波法残差修正的灰色模型能根据历史信息对残差权数进行动态修正，预测精度更高，适用性更强。利用改进后的模型对南京市未来几年的流动人口数量预测，结果表示2020年南京市流动人口数量将达到241.7838万人。

由于自适应滤波法的预测模型简便，能根据时间的变化对残差权数进行动态修正，而且可以利用计算机处理数据，所以此方法应用较为广泛，而灰色预测模型是解决信息量少的系统预测问题的有效工具。本文建立基于自适应滤波法残差修正的灰色模型，相较于传统的灰色预测模型具有更好的预测精度和适用性。基于自适应滤波法残差修正的灰色模型为城市流动人口的预测提供了一种简单而可靠的新路径，但基于自适应滤波法的改进模型仅从残差修正的角度提升了短期预测的精准度，而对于灰色预测模型中长期预测精度不高的问题，该改进方法还存在一定的局限性，因此还需要在后续研究中进一步完善和改进。

参考文献：

[1]Rumelhart D,McCelland J.Parallel Distributed Processing[M].Massachusetts：MIT Press,1986.

[2]李梦凡,张良.人口流动现象和城市化的影响因素——基于改进的乡-城人口流动模型的经济学分析[J].公共管理,2011，(11).

[3]张晓峒.计量经济分析[M].北京：经济科学出版社,2000.

[4]廖媛,何志芳,王明刚.改进的GM（1,1）模型在城市流动人口预测中的应用[J].科学技术与工程,2012,12(3).

[5]夏恩君,李森,赵轩维.北京市流动人口发展趋势预测研究[J].科技和产业,2015,(5).

[6]孙丽芹,常安定,位龙虎.基于AM残差修正的GM（1,1）模型的用水量预测[J].统计与决策,2016,(17).

[7]左明成,武云.自适应滤波在地震次声波信号中的应用研究[J].电子设计工程,2015,(8).