具无穷时滞的分数阶泛函微分方程可积解的存在性

勾明志，张 海

作为经典微积分的一种推广，分数阶微积分即是函数的任意阶导数与积分。由于分数阶导数算子具有记忆和遗传的特殊性质，利用分数微积分比整数阶微积分更能精准地描述动态系统的过程，目前与分数阶有关的常微分方程的研究已成为国内外学者关注的热点问题[1-5]。时滞是普遍存在的现象，时滞问题往往会影响系统的稳定程度和性能。近年来，关于时滞的分数阶微分方程的研究也取得了进展[6-7]。文献[6]利用不动点定理的方法推导出非线性分数阶泛函微分方程解的存在性条件，对整数阶常微分方程和泛函微分方程的初值问题进行了相应推广。在文献[7]中，Benchohra等讨论了下列隐式分数阶泛函微分方程可积解的存在性，

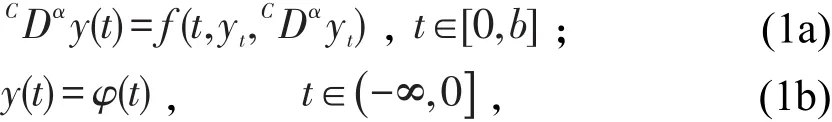
其中 0＜α＜1,f:J×B×B→R ，CDαy(t)表示 y的Caputo型α阶导数，B为拓扑空间，

受文献[6-7]的启发，本文主要讨论一类更广泛的具有无穷时滞的隐式分数阶泛函微分方程可积解的存在性问题：

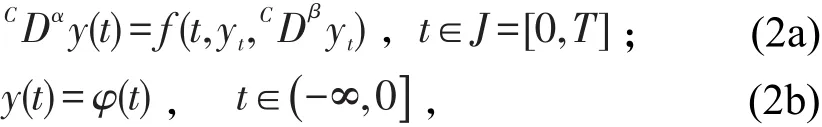
其中0＜β≤α＜1，f:J×B×B→R，CDαy(t)表示y的Caputo型α阶导数，B为拓扑空间，yt(θ)=y(t+θ),θ∈(-∞,0]。方程(2)中同时具有两个不同的分数导数，运用分析技巧，分别利用Banach不动点定理和Schauder不动点定理获得可积解的存在性条件，推广了文献[7]中的相应结果。

下面介绍分数微积分的概念和引理。

定义在区间J上的所有连续函数的Banach空间记为C(J,R)且范数定义为

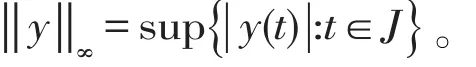
令L1(J,R)记作区间在J上的Lebesgue可积函数且范数定义为‖u=∫T| u(t)|dt。0

定义1[3]设 f∈L1( )[ ]a,b,R+，对∀α∈R+称

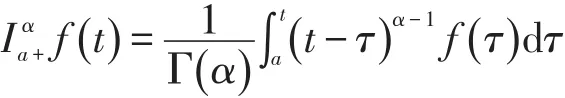
为 f(t)的 α 阶分数积分，其中 Γ(·)为Gamma函数Γ(z)=∫0+∞e-ttz-1dt,z＞ 0 。

定义2[3]设 f∈L1([ a ,b],R+)，对∀α∈(0 ,1]称

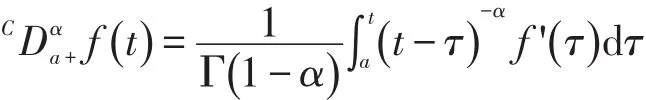
为 f(t)的α阶Caputo型分数导数。

性质1[3]令α,β＞0，t≥0，有如下性质成立：

(1) 令Iα:L1(J , R+)→L1(J , R+)，如果 f∈L1(J ,R+)有

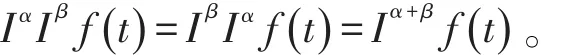
(2)如果 f∈Lp( )J,R+,1≤p≤+∞，有

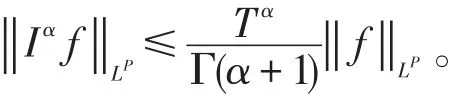
(3)分数阶积分算子具有线性性质

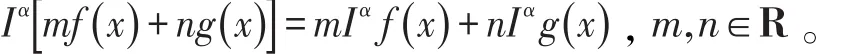
引理1[8]（Banach不动点定理）设(x,ρ)是一个完备的距离空间，T是(x,ρ)到其自身的一个压缩映射，则T在x上存在唯一的不动点。

引理2[7]（Schauder不动点定理）设E是一个Banach空间，Q是E的一个凸子集，T:Q→Q是列紧且连续，则T在Q上至少有一个不动点。

引理3[9]如果，0＜α＜1，则

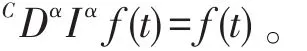
引理4[7](Kolmogorov列紧准则）令Ω⊆Lp(J,R),1≤p≤+∞，如果

(1)Ω在Lp(J,R)上有界；

(2)当h→0时，uh一致收敛于u，u∈Ω，其中，则 Ω 在 Lp上是相对列紧的。

引理5[10]设0＜α＜1,y(t)∈C([ 0 , T])且f(t , y(t))∈C([ 0 , T]×C[0 ,T ] )，则y是分数积分方程

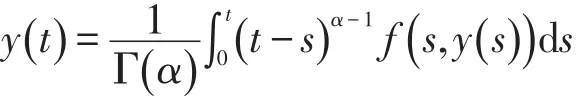
的解，当且仅当y为分数微分方程初值问题

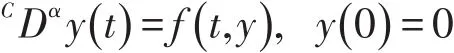
的解。

现在来定义方程(2)的积分等价方程。令空间

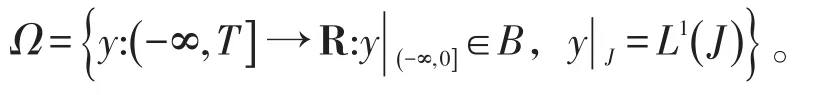
引理6满足初值问题(2)的等价分数阶积分方程为

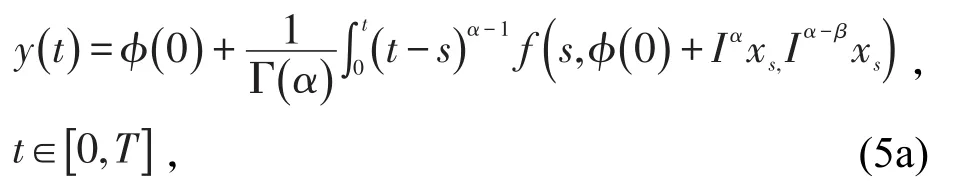
和初始条件

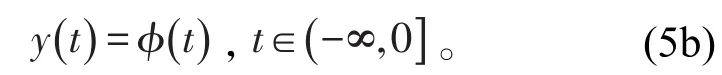
证明 显然，根据引理5，可得满足初值问题(2)的等价积分方程为

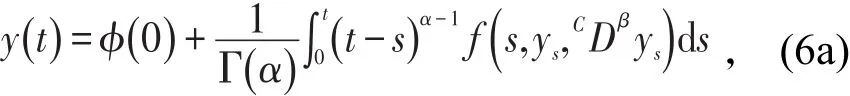
和初始条件

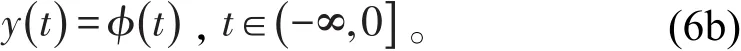
令CDαyt=xt，可得

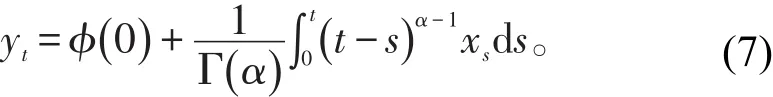
接下来计算

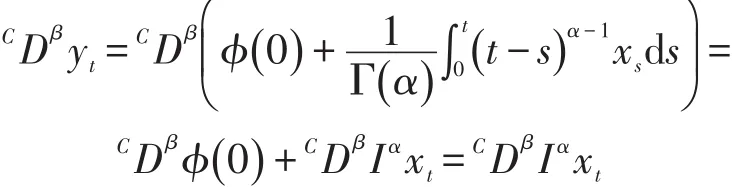
运用性质1可得

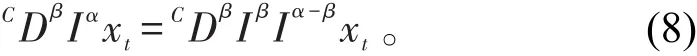
运用引理3可得

把(7)式和(9)式代入(6a)可得到(5a)。

在文中作(A)和(B)两项假设。

(A1)如果y:(- ∞,T ]→R且 y0∈B，则对∀t∈J满足下列条件：

(1)yt在B中，

(3) ||y()t≤H‖‖ytB，

其中H≥0的常数，K:J→[0 ,+∞ )为连续函数，M:[0 ,+∞ )→[0 ,+∞ )为局部有界函数，H，K，M，不依赖于y(·)。

(A2)对于函数y(·)在(A1)上，yt是一个在J上Banach空间内的连续函数。

(A3)空间B是完备空间。

(B)假设：f:J×B2→R，t∈J，且满足下列基本性质：

(B1)f:J×B2→R ，t∈J可测，在 t∈J中对任意的(u1,u2)∈B2且对所有的(u1,u2)∈B2连续。

(B2)存在常数k1＞0，k2＞0使得不等式

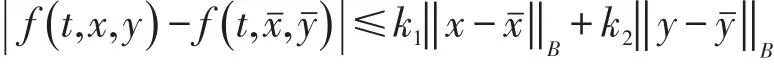
成立，其中 t∈J ，对 ∀x,xˉ,y,yˉ∈B 。还需令 Kb=sup{| k (t)|:t∈J} 。

(B3)存在一个非负函数a(t)∈L1(J)和常数q1＞0，q2＞0，使得下列不等式成立

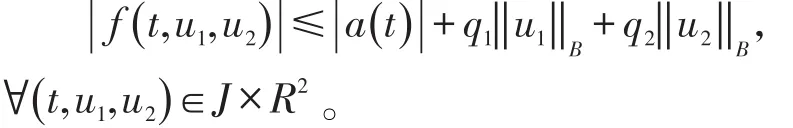
下面介绍本文的主要结果与证明过程。

分别运用Banach和Schauder两种不动点推导方程(2)解的存在性条件。首先利用Banach不动点讨论解的存在性。

定理 1 满足假设(A1)～(A3)，(B1)，(B2)，若＜1，则初值问题(2)在区间( ]-∞,T上存在唯一解。

证明 方程(2)可转化成不动点问题。定义算子N:Ω→Ω如下

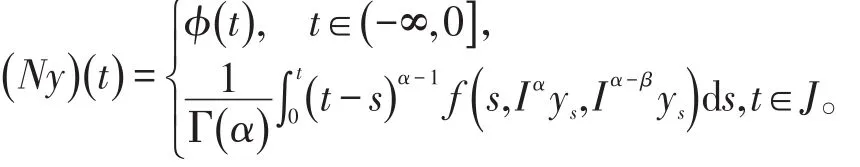
用Banach不动点定理来证明算子N有唯一不动点，令x(·):(- ∞,T ]→R定义为如下函数

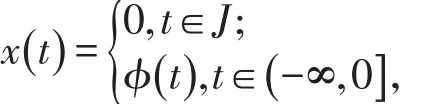
则x0=φ ；对于z∈L1(J ,R)，且z(0)=0 ，定义 zˉ为

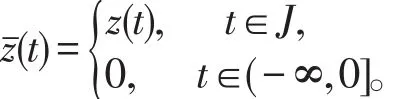
如果y()·满足分数积分方程

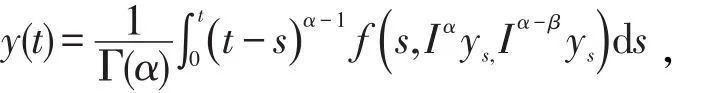
和初始条件y(t)=φ(t )，t∈(- ∞,0] ，则 y(t)=x(t)+zˉ(t)，t∈[0 , T]，可知对于每个t∈[0 , T ]，有 yt=xt+zˉt，则z(·)满足方程

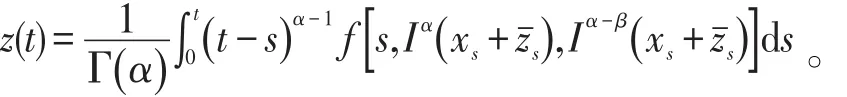
令L0={z ∈L1(J ,R):z0=0} 和 ‖· ‖b是在L0上的半范数，定义为

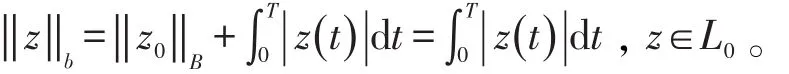
L0为Banach空间其范数为‖·‖b，定义算子Q:L0→L0为

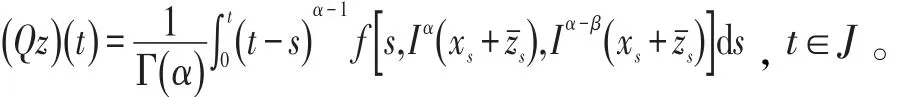
算子N有不动点就转化成了算子Q有不动点，即要证的是Q:L0→L0是压缩映射。

考察 z,z∗∈L0，对∀t∈，

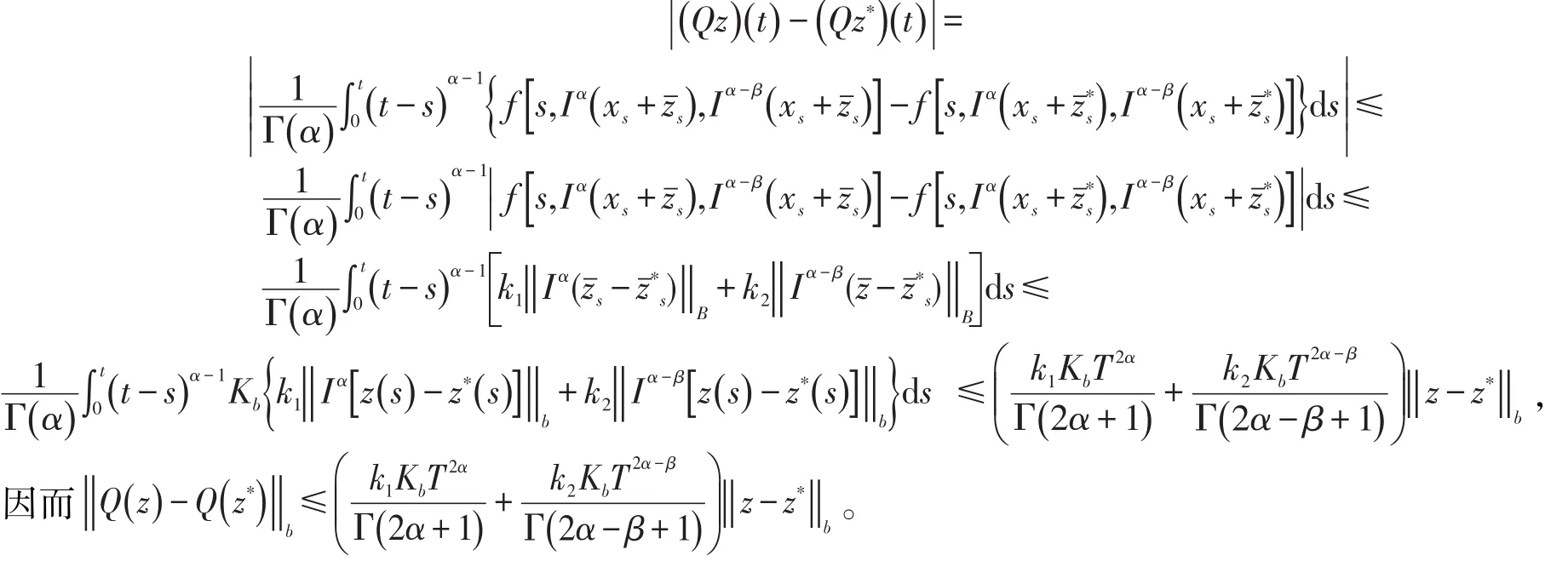
其次用Schauder不动点来获得解的存在性结果。

定理 2 满足假设(A1)～(A3)，(B1)，(B3)，若，则满足初值问题(2)的方程至少有一个解，其中y∈L1( )J,R。

证明 令P:L0→L0为定义在(5)中的映射

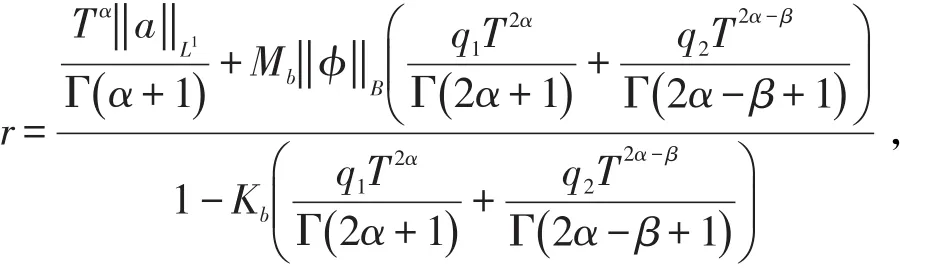
其中Mb=sup{| M (t)|:t∈J} 。

令Br={z∈L0,‖‖zb≤r}，显然Br是非空、有界、凸闭集合。只需验证算子P满足Schauder不动点定理的条件，此证明过程分为3步。

（i）P是连续映射。

令zn为L0上的zn→z的函数列，则

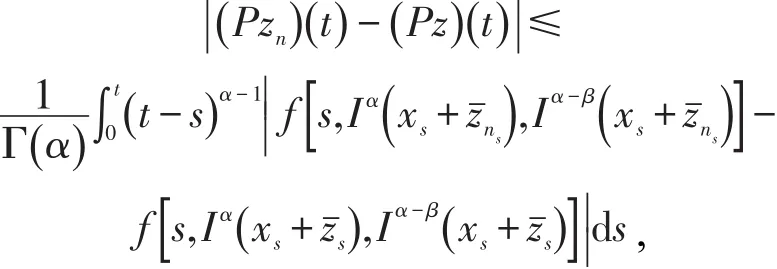
因为 f为连续函数，则当n→+∞时

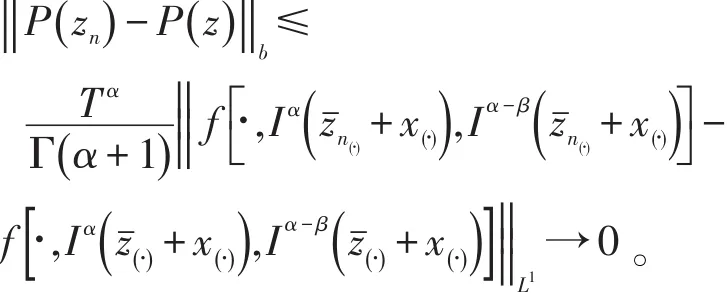
（ii）P是Br到其自身的映射。

令z∈Br。 f是一个连续函数，对于∀t∈[ ]0,T，有

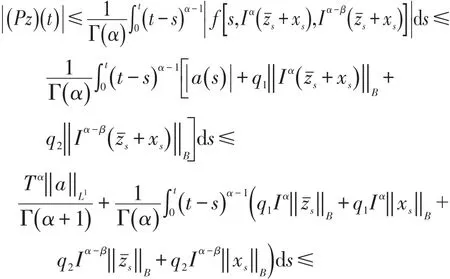
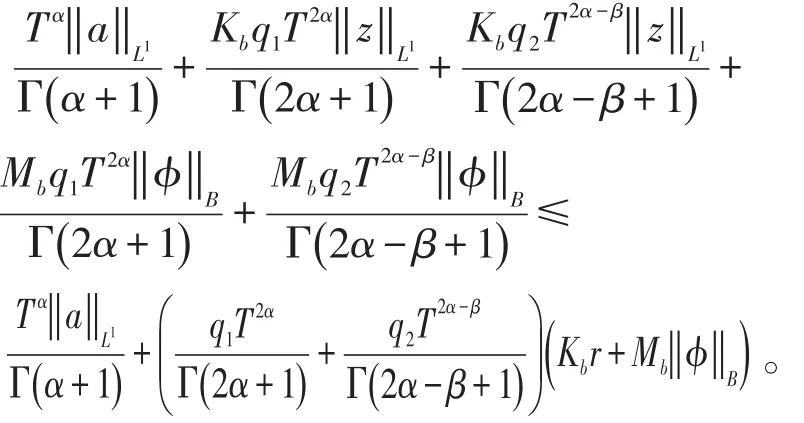
可得 ‖(P z) ‖L1≤r，即 PBr⊂Br。

（iii）P是列紧的。

PBr是相对列紧的，显然PBr在L0上是有界的，即满足Kolmogorov列紧准则中的条件(1)。下面证明有关Kolmogorov列紧准则中条件(2)。

在 L0中对∀z∈Br，有

当 z∈Br⊂L0和假设(B3)成立，即 f∈L0，通过性质1可得 Iαf∈L1(J,R)，有当h→0，t∈J时，

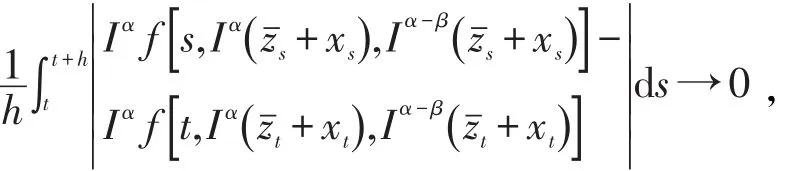
故(P z)h一致收敛于(P z)。

根据Kolmogorov列紧准则，PBr是相对列紧。由Schauder不动点定理，可知此映射至少有一个不动点，因而满足

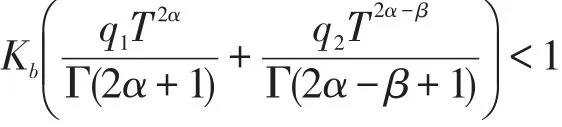
的方程(2)在Br中至少有一个解。

参考文献：

[1]MILLER K S,ROSS B.An introduction to the fractional calculus and fractional differential equations[M].New York：wiley-Interscience Publication,1993：126-174.

[2]PODLUBNY I.Fractional differential equations[M].Kosice：Technical University of Kosice,1999：159-195.

[3]KILBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and applications of fractional differential equations[M].The Kingdom of Netherlands：Elsevier,2006：135-212.

[4]DIETHELM K.The analysis of fractional differential equations[M].Berlin Heidelberg：Springer-Verlag,2010：85-132.

[5]BALEANU D,MACHADO J A T,LUO A C J.Fractional dy-namics and control[M].New York：Springer-Verlag,2012：109-133.

[6]张海,郑祖庥,蒋威.非线性分数阶泛函微分方程解的存在性[J].数学物理学报,2011,31A(2)：289-297.

[7]BENCHOHRA M,SOUID M S.Integrable solutions for implicit fractional order functional differential equations with infinite delay[J].Archivum Mathematicum,2015,51(2)：67-76.

[8]张恭庆,林源渠.泛函分析讲义[M].北京：北京大学出版社,2015：4-6.

[9]LI C P,DENG W H.Remarks on fractional derivatives[J].Applied Mathematics and Computation,2007(187)：777-784.

[10]EL-SAYED A M A.On the fractional differential equation[J].Applied Mathematics and Computation,1992,49(2-3)：205-213.

[11]HALE J,KATO J.Phase space for retarded equations with infinite delay[J].Funkcial Ekvac,1978,21(1)：11-41.