基于双观测站的水下机动目标被动跟踪

赵振轶, 李亚安, 陈 晓, 苏 骏



基于双观测站的水下机动目标被动跟踪

赵振轶, 李亚安, 陈 晓, 苏 骏

(西北工业大学 航海学院, 陕西 西安, 710072)

为了对水下机动目标进行航迹跟踪, 采用双观测站被动跟踪系统, 解决了单观测站利用纯方位角信息进行跟踪时的不可观测问题, 建立了目标状态方程和被动观测方程。将扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)与交互式多模型算法(IMM)相结合, 应用于被动跟踪系统中。仿真结果表明, 2种算法都能适用于水下机动目标被动跟踪。随着测量误差的增大, IMM-UKF算法比IMM-EKF算法表现出了更好的稳定性和更高的跟踪精度。

水下机动目标;双观测站;扩展卡尔曼滤波(EKF);无迹卡尔曼滤波(UKF);交互式多模型(IMM)

0 引言

随着水下信息对抗技术、目标机动性能的不断提高, 水下目标探测系统所面对的环境愈发复杂, 水下目标被动跟踪相较于主动跟踪方式具有隐蔽性好, 安全性高的特点, 从而在现代战争中拥有更高的生存能力。被动跟踪时仅利用目标发出的信号, 一般只能获得目标的方位角信息, 称为纯方位目标运动分析 (bearings-only target motion analysis, BTMA)问题[1]。在纯方位跟踪中, 经常使用单观测站机动来跟踪目标, 但要求单观测站机动性高于目标时才具有可观测性[2-3]。双观测站系统由于能够同时获得2个角度信息, 可以解决单静止观测站系统的距离模糊问题, 在静止时实现对目标的实时跟踪。

目标跟踪问题一般假设目标做匀速直线运动, 而当目标进行匀速转弯, 匀加速运动以及更复杂的机动运动时, 再使用匀速直线运动模型会造成较大的跟踪误差。针对机动运动的目标, 先后有多种跟踪模型被提出, 包括singer模型、“当前”统计模型、多模型以及交互式多模型(inte- racting multiple model, IMM)等[4]。其中, IMM算法[5]是较为常用的处理方法之一。IMM算法采用多个模型交互的方式进行估计, 对每个模型根据观测分配不同的概率, 其效果和实用性要优于采用单一模型的目标估计算法[6]。

近年来, 针对机动目标主动跟踪方式进行的研究较多[6-8]。主动跟踪时, 可以直接得到目标位置信息, 观测转移矩阵为线性, 因而精确度较高。进行纯方位被动跟踪时, 由于量测角度与目标运动参数之间的非线性关系, 需要采用非线性滤波器。卡尔曼滤波算法作为目标跟踪中常用的递推迭代类滤波算法有着很多扩展改进的衍生算法, 其中扩展卡尔曼滤波(extended Kalman filter, EKF)算法[9]和无迹卡尔曼滤波(unscented Kalman filter, UKF)算法[10]主要用来处理非线性问题。

将EKF和UKF滤波算法与IMM算法相结合, 应用到水下双观测站纯方位被动跟踪系统中, 用于跟踪机动运动的目标。通过仿真对跟踪效果进行分析, 结果显示, 双站纯方位系统在跟踪机动目标时, 使用IMM-UKF算法相较IMM-EKF算法有一定程度上的性能提升。

1 系统模型

1.1 双被动观测站跟踪机动目标模型

1.2 目标状态方程

1.3 观测方程

双站被动观测方程为

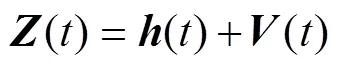
2 IMM算法

当目标机动运动时, 采用单一的匀速直线运动模型对目标进行航迹处理会产生很大的误差。需要针对目标的运动情况, 采取最适合的运动模型进行航迹处理。IMM算法是在广义伪贝叶斯算法基础上提出的一种根据马尔科夫概率转移矩阵进行多模型交互运算的跟踪算法[5]。IMM算法根据不同的目标运动状态分配给各个模型不同的加权概率, 通过各个模型的切换实现对目标的跟踪估计, 具有优于单一模型算法的跟踪性能[6-7]。

IMM算法分为4个主要部分, 包括交互输入、子滤波器滤波处理、各模型概率更新及交互输出。

1) 交互输入

协方差为

2) 子滤波器滤波

3) 各模型概率更新

4) 交互输出

将滤波器输出及更新后的模型概率交互计算, 得到最终的状态估计和协方差估计

3 适用于非线性系统的卡尔曼滤波算法

目标跟踪中常用的滤波算法是卡尔曼滤波算法, 该算法可以处理常规的线性问题。而对于纯方位被动跟踪系统面对的非线性问题, 就需要使用卡尔曼滤波算法的改进型算法: EKF算法[9]和UKF算法[10]。

3.1 EKF算法

与卡尔曼滤波不同的是, EKF利用泰勒级数展开原理, 对状态方程和观测方程求一阶偏导并忽略高阶项来进行近似线性化[8]。分为时间更新和量测更新, 其步骤如下。

党的十九大提出了“实施乡村振兴战略”，推进乡村振兴，实现农业现代化，必须加快农业机械化步伐。站在新的历史起点，农业机械化引领农业生产方式变革的态势更加趋显，河南农机化发展又迎来了重大历史机遇。

1) EKF时间更新

2) EKF量测更新

3.2 UKF算法

EKF算法的思想仍然是将问题线性化, 而UKF算法的提出, 使人们对与非线性问题有了新的处理方法[10]。UKF算法利用一些确定性的Sigma采样点, 在保证目标状态向量概率密度函数均值和协方差不变的情况下, 将这些Sigma采样点经过非线性系统转化(UT变换)后获得更加精确的后验均值和协方差。UKF算法步骤如下。

1) 进行Sigma点确定性取样

2) 确定均值和协方差权值

3) 目标时间更新

4) 目标量测更新

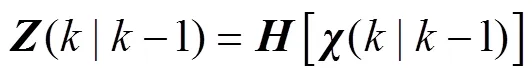
5) 状态及协方差估计

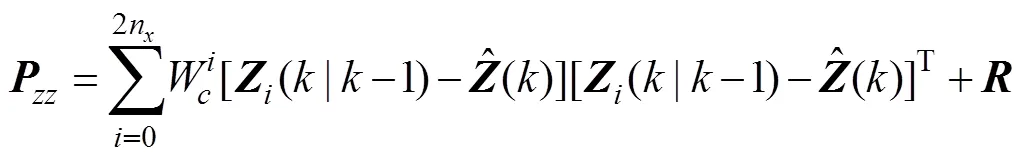
4 仿真结果及分析

4.1 仿真参数

假设观测站0坐标为[0, 0], 观测站1坐标为[1 000, 0], 水下目标速度约为40 kn, 跟踪目标时间550 s, 使用主动声呐探测水下目标时, 由于声波回波时间较长, 探测周期也会更长, 而被动探测时接收信号的周期可以很短。被动跟踪情况下采样间隔为1 s, 水下目标初始状态为

目标0~140 s作匀速直线运动, 140~180 s作角速度的右转弯运动, 180~300 s作匀速直线运动, 300~340 s作角速度的左转弯运动, 340~550 s作匀速直线运动。运动情况见图2。

模型状态转移矩阵

4.2 仿真结果及分析

分别选取不同测量角度误差标准差, 并使用2种算法计算跟踪均方根误差(root mean square error, RMSE), 仿真结果见表1。由表中数据可以看出在误差角度增大时, IMM-UKF算法较IMM- EKF算法有着更稳定精确的跟踪性能。

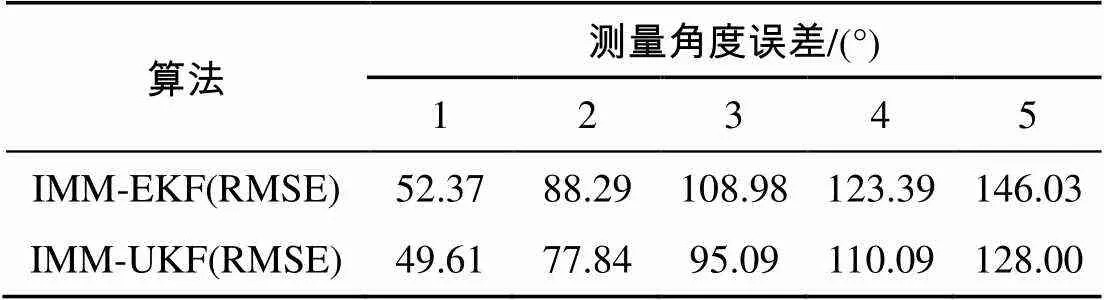
表1 不同测量角度误差时跟踪均方根误差

综合图表数据, 当目标距离较远, 测量角度误差较大或目标发生机动时, IMM-UKF算法跟踪效果比IMM-EKF算法跟踪效果更稳定准确。这是由于水下纯方位目标跟踪的非线性性质, EKF滤波时不可避免地产生了忽略高阶项带来的误差, 而UKF算法通过非线性传递函数避免了这类误差, 因而精度和稳定性较高。

5 结束语

在双观测站被动跟踪水下目标的情况下, 将EKF和UKF 2种滤波算法应用于IMM算法中, 用于处理机动目标跟踪问题, 对于双站被动观测系统的跟踪性能进行了分析。仿真结果表明, 被动的IMM-EKF和IMM-UKF算法在低测量误差情况下能够对水下机动目标进行有效跟踪, 而当测量误差增大时, IMM-UKF算法有着更高的稳定性和精度。

[1] Song T L. Observability of Target Tracking with Bearing- only Measurements[J]. IEEE Transactions on Aerospace and Electronics Systems, 1996, 32(4): 1468-1471.

[2] 丁薇, 李银伢. 不完全量测下的水下纯方位系统目标跟踪算法[J]. 计算机应用, 2015, 35(4): 1106-1109.

Ding Wei, Li Yin-ya. Target Tracking Algorithm for Underwater Bearings-only System with Incomplete Measurements[J]. Computer Applications, 2015, 35(4): 1109- 1109.

[3] 蔚婧, 文珺, 李彩彩, 等. 辅助变量纯方位目标跟踪算法[J]. 西安电子科技大学学报. 2016. 43(1): 167-172.

Yu-Jing, Wen Jun, Li Cai-cai, et al. Modified Instrumental Variable Method for Bearings-Only Target Tracking[J]. Journal of Xidian University, 43(1): 167-172.

[4] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991.

[5] Bar-Shalom Y, Chang K C. Tracking a Maneuvering Target Using Input Estimation Versus the Interacting Multiple Model Algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 296-300.

[6] 江宝安, 万群. 基于UKF-IMM的双红外机动目标跟踪算法[J]. 系统工程与电子技术, 2008, 30(8): 1454-1459.

Jiang Bao-an, Wan Qun. Maneuvering Target Passive Tracking with Dual Infrared Observers Using IMM Algorithm Based on UKF[J]. Systems Engineering and Ele- ctronics, 2008, 30(8): 1454-1459.

[7] 高文娟, 李亚安. 基于交互式多模型的水下机动目标跟踪[J]. 鱼雷技术, 2015, 23(3): 196-201.

Gao Wen-juan, Li Ya-an. Application of IMM to Under- water Maneuver Target Tracking[J]. Torpedo Technology, 2015, 23(3): 196-201.

[8] 刘娟丽. 基于交互多模型的被动多传感器机动目标跟踪算法研究[D]. 西安: 西安电子科技大学, 2010.

[9] 李彩菊, 李亚安. 扩展卡尔曼滤波与粒子滤波算法性能比较研究[J]．声学技术, 2009, 28(4): 74-78.

Li Cai-ju, Li Ya-an. Research of Comparative Analysis of Extended Kalman Filter and Particle Filter[J]. Technical Acoustics, 2009, 28(4): 74-78.

[10] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401- 422.

(责任编辑: 陈 曦)

Passive Tracking of Underwater Maneuvering Target Based on Double Observation Station

ZHAO Zhen-yi, LI Ya-an, CHEN Xiao, SU Jun

(School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)

For tracking underwater maneuvering target, a passive tracking system with double observation station is used to solve the unobservable problem of single observation station due to tracking with bearing angle-only information. The target state equation and the passive observation equation are established. The extended Kalman filter(EKF) and the unscented Kalman filter(UKF) are combined respectively with the interactive multiple model(IMM) algorithm to serve the passive tracking system with double observation station. Simulation results show that both IMM-UKF and IMM-EKF algorithms can be applied to passive tracking of underwater maneuvering targets. The IMM-UKF algorithm exhibits higher stability and tracking accuracy than the IMM-EKF algorithm with the increase of measurement error.

underwater maneuvering target; double observation station; extend Kalman filter(EKF); unscented Kalman filter(UKF); interactive multiple model(IMM)

TJ630; TP391.99

A

2096-3920(2018)01-0040-06

10.11993/j.issn.2096-3920.2018.01.007

赵振轶, 李亚安, 陈晓, 等. 基于双观测站的水下机动目标被动跟踪[J]. 水下无人系统学报, 2018, 26(1): 40-45.

2017-07-19;

2017-09-01.

国家自然科学基金项目资助(5140921).

赵振轶(1993-), 男, 在读硕士, 主要研究方向为水下信息处理和目标跟踪